基于变模式分解的爆震特征识别方法*

毕凤荣， 李 鑫， 马 腾

(天津大学内燃机燃烧学国家重点实验室 天津，300072)

引 言

小型强化技术是提高发动机性能的一项重要技术措施，但是也会导致汽油机爆震趋势的上升，降低性能，同时轻微爆震却能改善发动机的动力性与热效率[1]，因此需要对发动机爆震进行精确检测，这对提高发动机性能有重要意义。工程上常利用缸盖振动信号对爆震进行检测，但是原始振动信号需要进行一定处理才能在大量噪声中提取出爆震特征[2]，在目前的研究中，常用的自适应信号处理方法有经验模态分解(empirical mode decomposition，简称EMD)等，但是这种类型的算法均存在一定程度上的模态混叠[3-4]、端点效应[5]、过/欠包络等现象[6-7]。

Dragomiretskiy等[8]提出了一种新的信号自适应分解方法——变模式分解(variational mode decomposition，简称VMD)，这种方法的整体框架是变分问题，要求每个模态的估计带宽之和最小，其中假设每个模态是具有不同中心频率的有限带宽，并采用交替方向乘子法，不断更新各模态及其中心频率，逐步将各模态解调到相应的基频带，最终各个模态及相应的中心频率被一同提取出来。VMD算法具有坚实的理论基础，其实质是多个自适应维纳滤波组，表现出更好的鲁棒性；通过合理控制收敛条件，VMD的采样效应也远小于EMD方法[9-11]。

1 VMD算法的原理

VMD算法中，模态函数被定义为一个调幅-调频信号uk(t)，假设每个模态具有中心频率且带宽有限，则变分问题为寻找K个模态函数uk(t)，使得每个模态的估计带宽之和最小，约束条件为各模态之和等于输入信号f。具体的过程如下所示[8-11]。

通过Hilbert变换，得到每个模态函数uk(t)的解析信号，目的是得到其单边频谱

(1)

对各个模态解析信号混合一个预估中心频率e-jωkt，将每个模态的频谱调制到相应的基频带

(2)

计算以上解调信号梯度的平方L2范数，估计出各模态信号带宽，受约束的变分问题如下所示

(3)

在求解变分问题时，首先需要引入二次惩罚因子α和拉格朗日乘法算子λ(t)，将约束性变分问题变为非约束性变分问题，其中二次惩罚因子可在高斯噪声存在的情况下保证信号的重构精度，拉格朗日算子使得约束条件保持严格性，拓展的拉格朗日表达式如下

(4)

接着执行循环。

根据式(5)更新uk

(5)

根据式(6)更新ωk

(6)

根据式(7)更新λ

(7)

重复上述步骤，直至满足式(8)

(8)

整个循环结束，得到K个模态分量。

2 VMD算法的验证

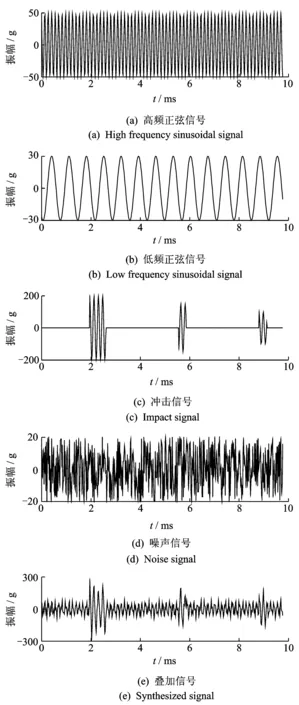
图1 模拟信号Fig.1 A simulated signal

为验证VMD算法对比EMD算法的优越性，文中分别使用两种算法对模拟信号进行分析。模拟信号如图1所示，其分别由两组不同的正弦信号、一组冲击信号与一组噪声信号组成。首先对其进行VMD分解，根据模拟信号的组成，并考虑到所加噪声较为复杂，通过比较，此处选择分解层数为K=5较为合理，EMD算法分解层数根据收敛条件自动获得，最终得到EMD分解结果为7层。

为方便对比，对EMD结果在文中只展示出前5阶分量，其分解结果如图2，3所示。由上图可以看出，VMD可以较为准确地将原信号中的高频正弦信号、低频正弦信号、冲击信号分离出来，而EMD方法仅能观察到冲击特征，而其他信号分量并不明显。

图2 VMD分解结果图Fig.2 The composition results of VMD

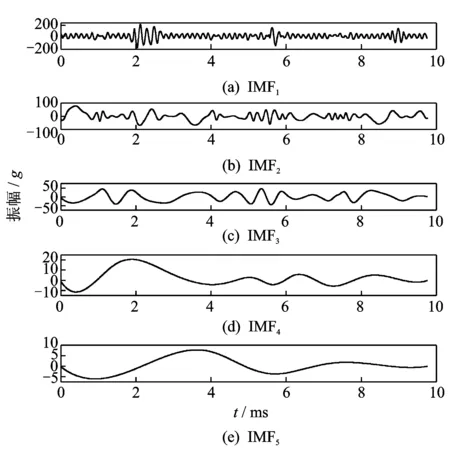
图3 EMD分解结果Fig.3 The composition results of EMD

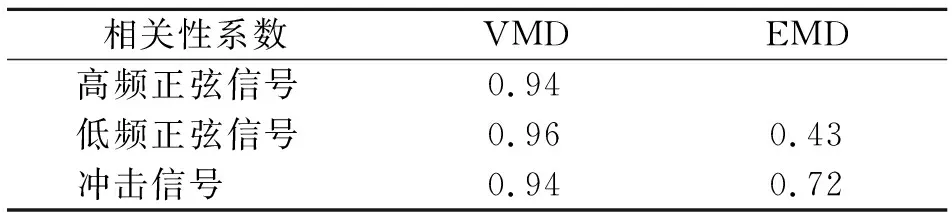
为进一步对信号分解的准确程度进行度量，笔者计算了两种算法中各个模态分量与对应的原信号分量的相关性系数，具体如表1所示，可以看出VMD算法准确性较高。

表1分解信号与原信号的相关性系数

Tab.1Thecorrelationcoefficientbetweendecomposedsignalandoriginalsignal

相关性系数VMDEMD高频正弦信号0.94低频正弦信号0.960.43冲击信号0.940.72

3 自适应分层的VMD算法

在VMD算法的研究过程中，笔者发现对原信号的分解层数K对分解结果有着十分重要的影响，若选择K不当，会直接导致信号过分解或欠分解[8]。但是原始的VMD算法并未给出一个明确的分解层数的选择标准，所以在实际分解过程中分解层数往往需要人为选择，带有很大的主观性。

根据上文对VMD原理的描述，可以发现VMD分解与信号中心频率有着密切的关系。因此笔者提出了一种基于中心频率并适用于爆震信号分解的可以自适应选择分解层数K的VMD算法。

笔者选取了某型号汽油机爆震时的缸盖振动信号，如图4所示。文中分别对此信号进行3，4，5，6层分解，并计算在不同的分解层数K的情况下得到每阶分量信号的中心频率，结果如表2所示。

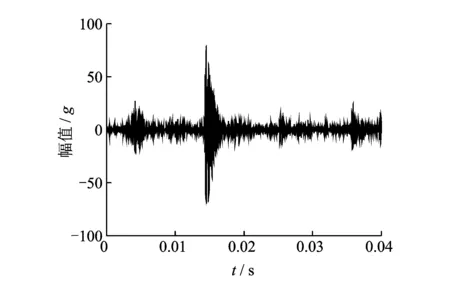
图4 爆震工况下缸盖振动信号Fig.4 The cylinder head vibration signal under the condition of knock

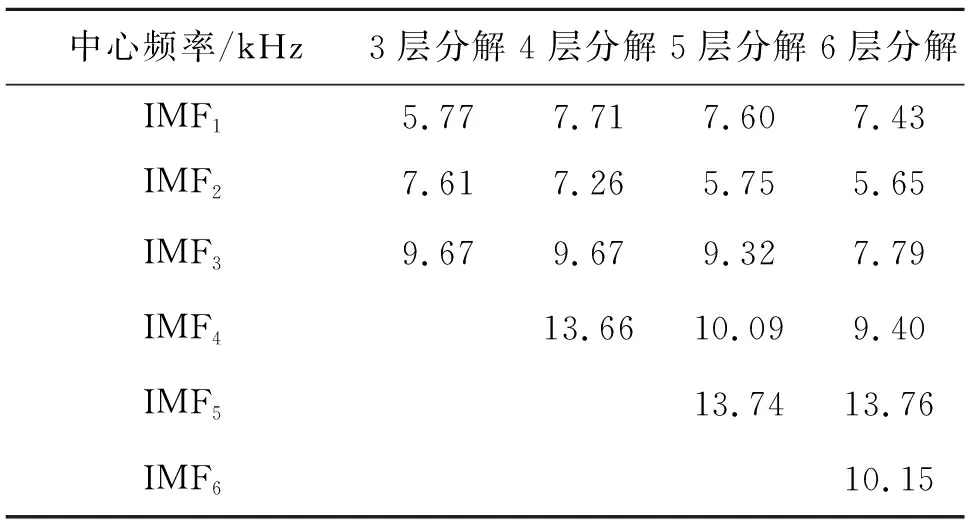
中心频率/kHz3层分解4层分解5层分解6层分解IMF15.777.717.607.43IMF27.617.265.755.65IMF39.679.679.327.79IMF413.6610.099.40IMF513.7413.76IMF610.15

通过对原始信号与经过分解得到的分量的分析，可知此实验用汽油机的爆震特征频率主要处于7～15 kHz的几个频带内，又根据对各个分量振幅大小的分析，发现中心频率处于7.7 kHz附近的分量信号的冲击成分振幅要远大于其他分量，最能表征爆震特征。因此选择此分量作为特征分量，则在分解层数分别为3，4，5，6的VMD分解中，其特征分量分别为第2，1，1，3阶分量。随着分解层数的变化，非特征分量与特征分量所处频率段的重叠程度也会发生变化，因此计算了在上述不同K取值的情况下非特征分量与特征分量之间中心频率的差值(绝对值)。具体结果如表3所示：

表3非特征分量与特征分量中心频率差值

Tab.3Thedifferenceofcenterfrequencybetweencharactercompontentandothercomponents

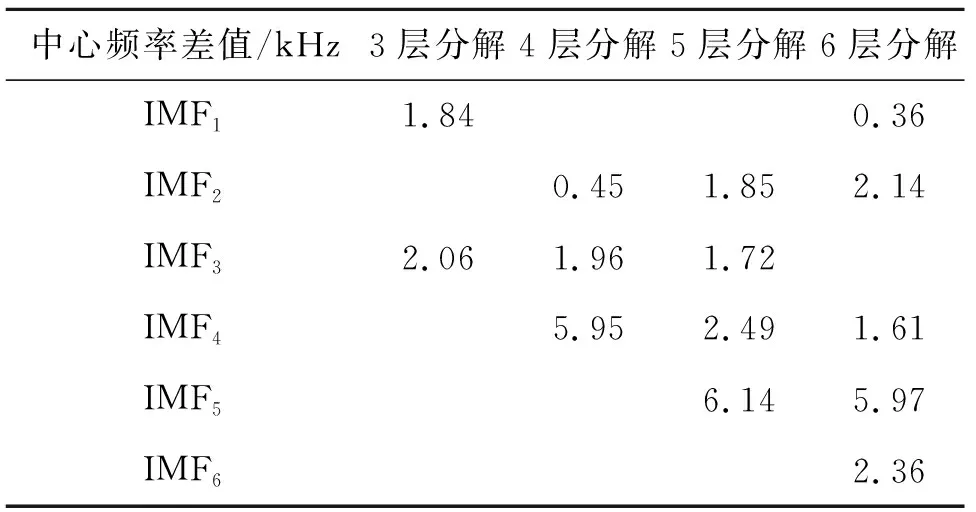
中心频率差值/kHz3层分解4层分解5层分解6层分解IMF11.840.36IMF20.451.852.14IMF32.061.961.72IMF45.952.491.61IMF56.145.97IMF62.36

观察表3，笔者考察了各阶非特征分量与特征分量所处频率段的重叠程度，发现可以用上述中心频率差值(绝对值)的最小值来表征：当此最小值过小时，重叠程度过大即出现过分解现象，冲击成分被分解到不同的分量中；而当此最小值过大时，各阶分量频率段过于分散，会出现欠分解现象即会有较多噪声成分存在于特征分量中。以上述结果为基础，发现在使用VMD对爆震工况下缸盖振动信号分解时，当每阶非特征分量中心频率与特征分量中心频率差最小值在1.5～1.8 kHz时，特征分量可以更为准确地表征爆震，故将此中心频率差值范围作为判断分解停止的条件。而上文中分解层数为5时为最优，中心频率差值的最小值为1.72 kHz。

为验证上述方法的正确性，笔者在实验中采集了上述发动机在1 000～4 800 r/min转速范围内不同点火提前角下的振动信号，经过筛选选取转速为1 600 r/min，点火提前角比正常点火提前角增大10°工况下的一段未经滤波的原始信号，如图5所示。图中展示了在某一循环中4个汽缸分别导致的冲击情况，根据原始缸压信号得知，在四段冲击成分依次对应缸内燃烧情况分别为轻微爆震、强烈爆震及两段正常工作。而直接从原始信号分析，只能观察到此工况下有一缸存在强烈爆震，其他三缸的情况无法判断。

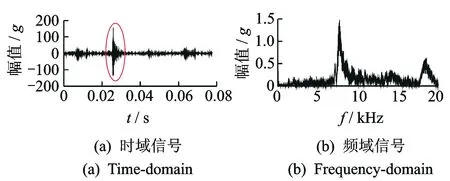
图5 爆震工况下缸盖振动信号Fig.5 The vibration signal

现将这段试验信号分别进行VMD，EMD分解，结果为VMD分解得到4阶分量，EMD分解得到12阶分量，限于篇幅不再全部展示。从分解层数上看出，VMD算法相比EMD算法更为简洁。为对比文中又分别对两种算法分解得到的特征分量进行傅里叶变换，得到其频谱图，如图6，7所示。

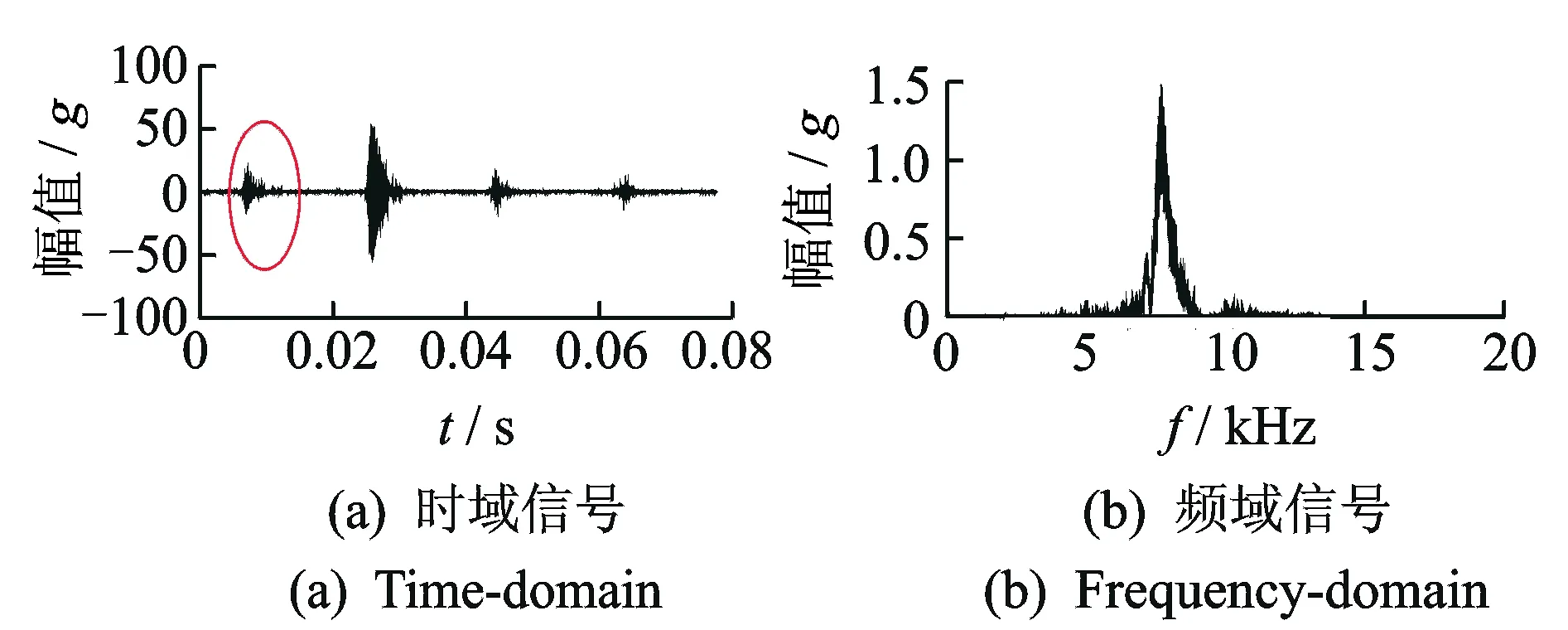
图6 VMD分解特征分量Fig.6 The characteristic part of VMD

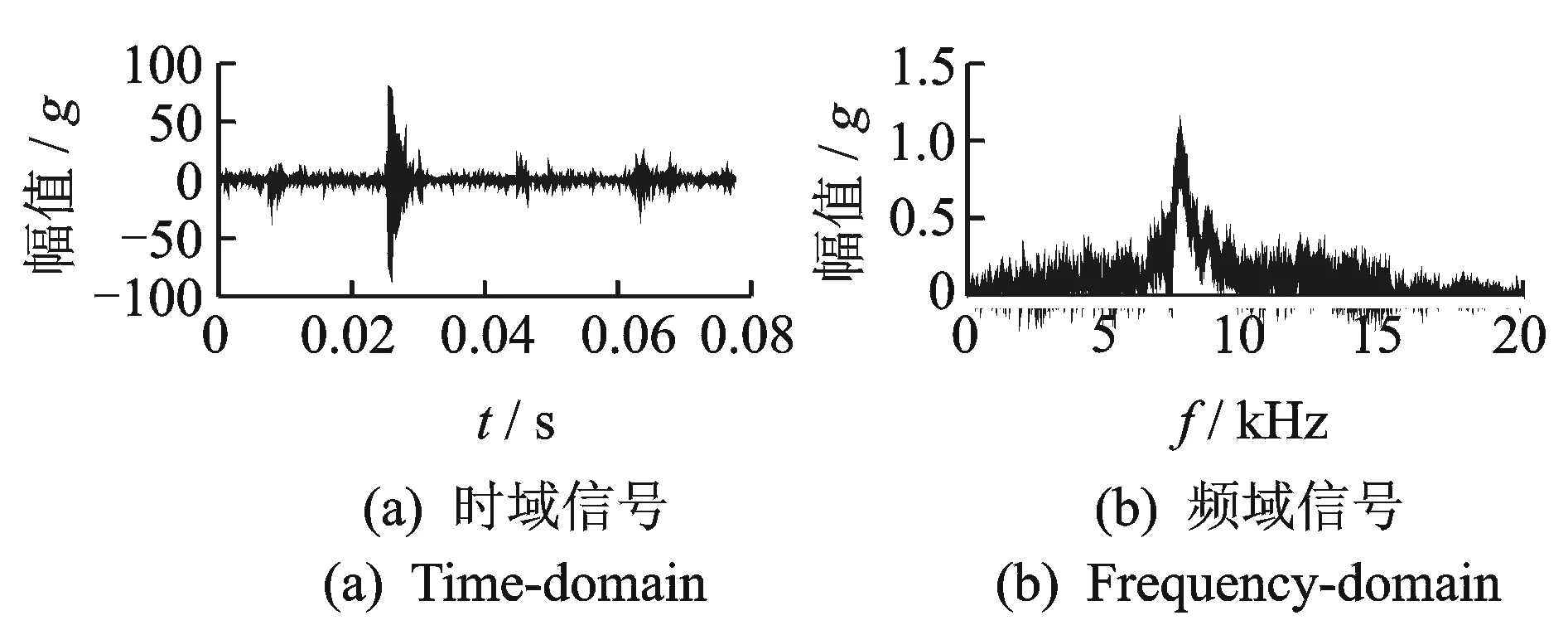
图7 EMD分解特征分量Fig.7 The characteristic part of EMD

从以上对比看出，在未经滤波的情况下，VMD算法获得了较为理想的窄带信号。虽然VMD与EMD都可以识别出强烈爆震工况，但在VMD得到的特征分量中可以识别出轻微爆震工况，在EMD的特征分量中轻微爆震和正常工况仍然无法区分。究其原因， VMD算法得到的特征分量的频率段更为集中于爆震特征频段，表明VMD算法可得到混有噪声成分非常少的更为准确的特征分量；而EMD分解得到的特征分量，其频率成分相对复杂，混有的噪声成分较多，且在EMD分解获得的结果中还出现了模态混叠与虚假分量现象。在爆震特征提取中，主要减小特征分量中的低频噪声成分，以显示高频冲击成分，达到准确提取爆震特征的目的。由此看出，VMD算法在爆震特征提取中较EMD算法有较为明显的优越性。

4 结束语

笔者首先利用VMD与EMD对一段模拟信号进行分解，通过对比分解结果中各分量与原信号成分的相关性系数，证明了VMD算法在信号分解中的优越性。笔者发现VMD算法的准确度与分解层数关系密切，但是并不存在一个对分解层数的公认选择标准。所以，通过分析待分解信号的各阶分量的中心频率，提出了一种通过中心频率差值来自适应确定分解层数的方法。即利用VMD算法对信号从一个较低的层数开始进行分解，逐个增加分解层数，直至分解结果满足预先设定的阈值为止。经过验证，笔者提出的优化VMD方法在爆震特征提取中对比EMD方法存在明显优势。由VMD分解得到的特征分量的冲击成分的振幅较其他算法获得的结果振幅较小，这与其自身频率较为集中，基本不存在噪声有很大关系，这也意味着需要一种与之适应的爆震强度指标，这将是今后的工作方向。