基于Delaunay的飞机发动机机匣应变重构及数据处理

王昆 刘客嘉

摘要：结构健康检测中，我们需要重点关注关键区域。但是由于结构自身或者是工作环境等因素影响，我们无法在关键部位加装检测元件。为此，针对发动机匣，提出了基于Delaunay的应变重构方法，旨在获得整个检测区域的应变信息。同时，为了方便人工处理，对数据进行了可视化处理。通过预先布置的传感器进行数据采集，经过经验模态分解滤波，结合检测区域的位置数据，实现应变重构和数据可视化。最后，以发动机风扇机匣为例，实现了应变重构并进行了数据对比，分析了重构结果的有效性和准确性。

关键词：应变重构；飞机机匣；三角剖分

中图分类号：TP39 文献标识码：A 文章编号：1007-9416（2018）06-0067-02

1 引言

飞机在服役过程中，恶劣的工作环境容易导致结构件损坏，轻则产生故障、任务失败，重则机毁人亡。发动机机匣作為航空发动机的重要部分，是整个发动机的基座，也是航空发动机的主要承力部件。发动机机匣在工作状态下，主要承受气体负荷和质量惯性力，其次还要承受热负荷，声负荷以及一些装配应力[1]。机匣的状态反映了发动机的工作状态。对发动机机匣进行健康监测，能极大提升飞行安全。

应变重构是指通过检测得到的有限点的离散信息，通过计算得到检测部位的应变场信息。常见的方式有两种，一种是根据离散信息进行插值，另一种是结合结构模型进行力学分析。但是由于实际的工作环境中，结构本身的复杂性以及受载的多变性等问题。本文选择使用插值方法，使用Delaunay三角剖分插值进行应变重构。

2 Delaunay三角剖分

Delaunay三角剖分在计算几何学当中占有非常重要的地位，在众多的领域当中都有非常高的实用价值。在有限网格生成、实体边界模拟、图形图像处理和三维实体几何造型等众多应用领域当中，大量使用Delaunay三角剖分算法用来解决这些领域当中存在的问题[2]。

本文选用三角网生长法[3]。将一个空间数据点作为起始点，逐步扩张形成覆盖所有点集的三角网，形成仅有散点构成的四面体几何网络。将整个区域四面体化后，便可以对整个散点云（xi，yi，zi，ti）进行插值[4]。为了便于理解，我们将散点数据（xi，yi，zi，ti）描述为每个点（xi，yi，zi）以及其测量的温度ti。

3 应变重构

人脑对视觉信息的处理要比书面信息容易的多。当我们针对数据进行分析时，使用图表来总结复杂的数据，可以确保对数据的理解比那些混乱的报告或电子表格更快。所以，本文以可视化的形式，将数据转换成图形显示，增强理解。

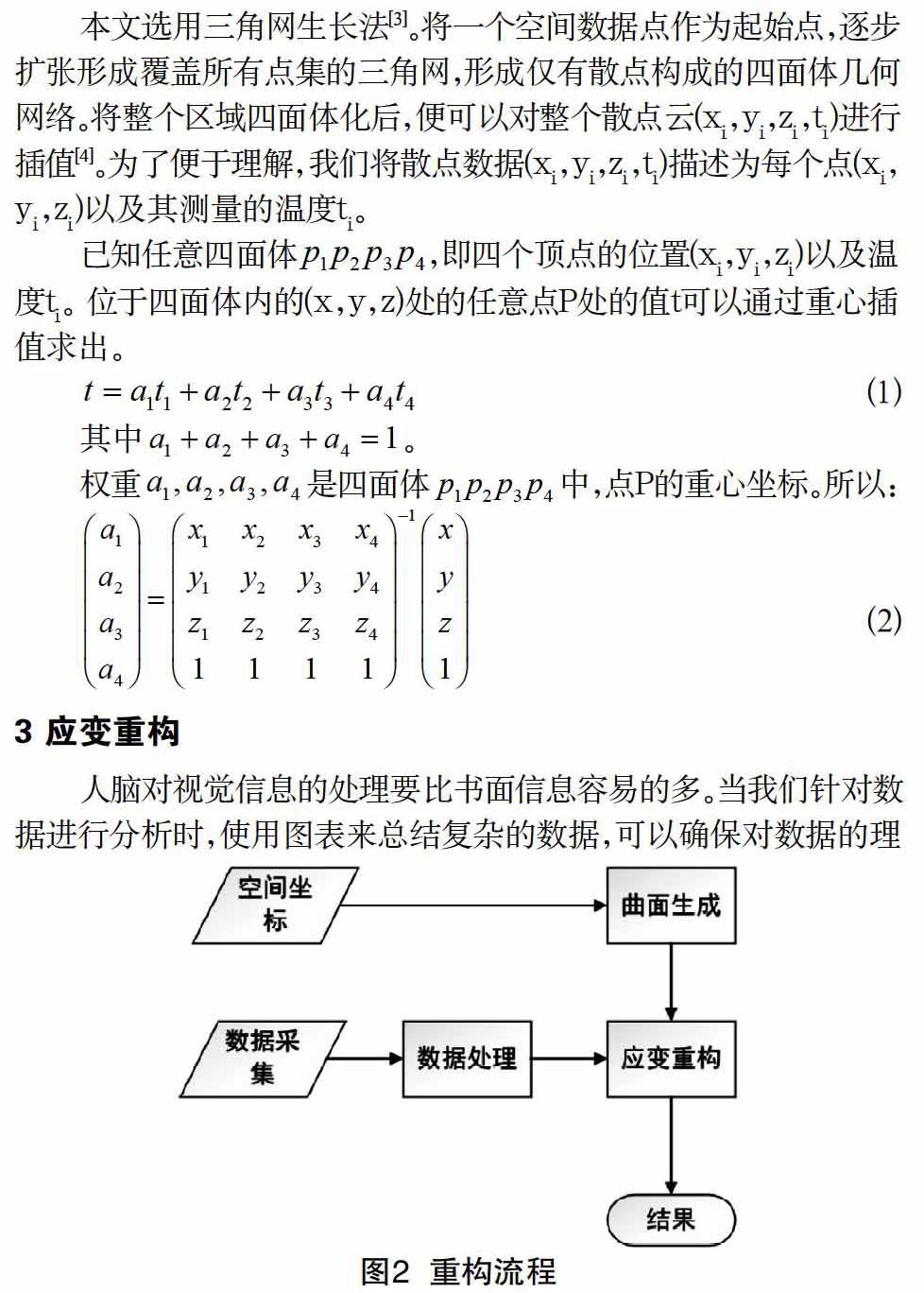
整个重构流程如图2所示。首先获取监控区域的散点坐标，生成检测区域的网格坐标和曲面。然后将传感器获取的应变数据进行处理，再结合网格曲面，基于四面体插值，最终获得的应变重构结果。

本文以发动机风扇机匣为例，如图3所示，针对图中已选择表面进行试验。

3.1 实体可视化

为了实现对检测区域的可视化，首先要实现检测区域的可视化。首先第一步要获取表面的空间坐标信息，通过三坐标检测，或是通过建模导出等方式，我们可以获得大量检测区域的离散坐标。根据Delaunay三角剖分，便可拟合检测区域。本文采用通过建模的方式，获得监测表面的空间数据。结果如图4所示。

3.2 数据可视化

传感器采集得到的数据中，包含了工作环境的噪声干扰，为此，我们还需要对收集的信号进行滤波处理。本文采用EMD滤波。

经验模态分解（EMD）方法是HUANG等人于1998提出的一种信号分析方法。它依据数据自身的时间尺度特征来进行信号分解，与建立在先验性基函数的小波分解方法有本质区别，在处理非平稳、非线性数据上具有非常明显的优势。EMD将复杂信号分解为有限个本征模态函数，所分解出来的各个IMF分量包含原信号的不同时间尺度的局部特征信号，可以将其看作是时空滤波过程，利用这个性质可以对信号进行滤波分析和降噪处理[5]。

将滤波得到的应变信息，结合前一步得到的空间网格，根据Delaunay插值方法，进行应变重构，最终获得的结果如图5所示。

选取10个数据点与预先设置的测量点进行对比，结果如图6所示，其中蓝色十字为实际测量数据，红色圆圈为重构数据。从表1相对误差表中，我们可以看出，数据一致性较好，实测应变数据基本吻合。

4 结语

针对机匣应变场监测需求，本文提出了基于Delaunay三角剖分的应变场重构方法。以机匣部分表面为例，进行了试验。试验结果显示，重构结果与真实数据有较好的一致性。但是在检测区域的端点部分，会出现数据丢失的情况，这是由于凸包性导致无法插值。后续的工作主要针对测量点布局的优化，以及端点数据的处理，以便获得更加准确的空间应变场。

参考文献

[1]温登哲，陈予恕.航空发动机机匣动力学研究进展与展望[J].动力学与控制学报，2013，11（01）：12-19.

[2]伯格，计算几何算法与应用（邓俊辉译）[M].北京：清华大学出版社，2005.

[3]李丽.三维空间Delaunay三角剖分算法的研究及应用[D].大连海事大学，2010.3.

[4]I. Amidror， "Scattered data interopla-tion methods for electronic imaging systems： a survey，" Journal of Electronic Imaging， vol. 11， （2）， pp. 157-176， 2002.4.

[5]程诚，程晶晶，王光伟，薛志波.EMD滤波方法在NMR测井中的应用[J].武汉理工大学学报（信息与管理工程版），2014，36（02）：176-179+206.

Abstract：In structural health monitor， we need to focus on some important areas. However， limited by some factors such as the structure itself or the working environment， we cannot apply sensors on those areas. To solve this problem， we propose a method of strain reconstruction based on Delaunay for the aeroengine casing， aiming to obtain the strain information of the entire detection area. In order to facilitate manual processing， the data is visualized. Firstly， the data is obtained through pre-arranged sensors， and then it is subjected to empirical mode decomposition and filtering. Finally， with the position data， realize strain reconstruction and data visualization. In the end， a strain reconstruction of aeroengine casing was provided and the validity and accuracy of the data was analyzed.

Key words：strain reconstruction；seroengine casing；triangulation