基于点对应的关节软骨厚度变化跟踪方法
2018-10-31陈彦百郭长勇程远志
陈彦百, 郭长勇, 程远志
(哈尔滨工业大学 计算机科学与技术学院, 哈尔滨 150001)
引言
在骨关节炎的发病过程中,患者关节软骨的厚度以及形态会随着病情的发展而发生变化。通过MR图像测定骨关节炎患者的关节软骨厚度变化以及对其进行形态描述,已经成为骨关节炎的诊断和治疗中最广泛使用的生物标志[1-3]。研究显示,在一定时间段内软骨厚度的变化属于局部变化,而不是整体的厚度变化[4-5]。
为了观测关节炎患者病情变化,本文从MR图像中跟踪关节软骨微小部位的厚度变化来展开预测。首先要采集不同时间扫描关节的MR图像;然后对关节软骨进行分割。在骨关节炎的发病过程中,关节软骨外表面受到磨损,而在大部分发病阶段,软骨-股骨面依然保持原有正常形状和特点,并未受到磨损[6]。因此可以使用软骨-股骨面作为参照基准,先得到骨-软骨交界面两个点云(集),然后计算出该点的关节软骨厚度,最后计算各点的软骨厚度差,但前提是知道两个点云中各点的对应关系,因此研究随即演变为需要求解2个点云中各点的对应关系,也就是转化成了一个点对应问题。
1 点对应问题的数学描述
首先给出点对应问题的数学描述:
设A、B分别为n维空间Rn的2个有限集合,A={x1,x2,…,xp},B={y1,y2,…,yq},A0⊆A。点对应问题就是找一个从A0到B的映射P(或一个从A到B的部分映射P),使:
∀xi∈A0P(xi)=yj
(1)
但其中,A0与A0中的xi所对应的yj均是未知的。
已知映射是一个特殊的二元关系,而二元关系可以用关系矩阵表示,因此,从A到B的部分映射P可以用一个p×q关系矩阵来表示,该矩阵在点对应问题中一般称为分配矩阵,当分配矩阵为方阵时称为配置矩阵,其中:
(2)
说明:
(1)从点对应问题的数学描述来看,找到的对应可能存在一个元素对应多个元素的情况。但在实际问题中,往往希望这种对应是一对一的,而且可能要求A(或B)中的元素都存在对应,这种对应就是从A到B单射或从B到A的单射。如果2个集合A,B中的元素一样多,则这种对应就是从A到B的双射。
(2)很容易证明以下结论:
① 从A到B的部分映射P总共有(q+1)p,从A到B的映射P总共有qp个。
② 如果p
③ 如果p=q,则从A到B的双射P总共有p!。
虽然从一个有限集合到另一个有限集合的部分映射、映射、单射和双射的个数都是有限的,但不要试图通过穷举法一一列出映射P,并验证其是否符合要求来求解点对应问题,因为还未生成有效的生成算法将所有可能的部分映射、映射、单射穷举出来。对于双射,虽能将双射的穷举转化成全排列的生成问题,进而利用全排列的生成算法,如:字典序法、递增进位制数法、递减进位制数法、邻位对换法等完整地将所有可能的全排列无重复、无遗漏地穷举出来,但当p或q较大时其计算量巨大,以致在允许的时间内无法得到最终优化解。
考察一个映射的映射图:设A={a,b,c,d},B={u,v,x,y,z},f是一个从A到B的一个映射:f(a)=y,f(b)=z,f(c)=u,f(d)=x,具体如图1所示。

图1 函数图
从图论的角度看,图1就是一个顶点集V=A∪B。进一步分析,不难得出:寻找A到B的一个(部分)映射就是从A∪B为顶点集的偶图中寻求匹配。于是,点对应问题就转化为偶图的匹配问题。
定义1G=(V,E)称为偶图,如果G的顶点集V有一个二划分{V1,V2},使得G的任一条边的2个端点在V1中,另一个在V2中,偶图记做(V1∪V2,E)。
如果∀u∈V1,v∈V2均有u,v∈E,则这个图称为完全偶图,并记为Km,n,其中|V1|=m, |V2|=n。
定义2设G=(V,E)是一个图,则:
1)G的任2条不相邻的边x与y称为相互独立的。
2)若Y⊆E,且Y中任2条边都是相互独立的,则称Y为G的一个匹配。
3)设Y是G的一个匹配,若对G的任一匹配Y′,恒有|Y′||Y|,则称Y是图G的一个最大匹配。
定义3设G=(V1∪V2,E)是一个偶图,若存在一个匹配Y使得|Y|=min{|V1|,|V2|},则称Y是偶图G的完全匹配;若|V1|=|V2|,则称Y为G的一个完美匹配。
相应地,找一个使对应点尽可能多的部分映射就是找最大匹配,找单射就是找完全匹配,找双射就是找完美匹配。在实际问题中,最常见的就是涉及最大匹配和完全匹配的问题,当然,一般是找满足一定(最优)条件的最大匹配和完全匹配。
偶图的最大匹配有2种求法,分别是:网络最大流算法和匈牙利算法。匈牙利算法本质上还是网络最大流算法,只是将依据偶图匹配这个问题的特点,把最大流算法做了简化,提高了效率。最大流算法的核心问题就是找增广路径,匈牙利算法也不例外。
一般情况下,找到一个偶图的最大匹配并不意味着点对应问题已经解决。通常一个偶图的最大匹配并不只有一个。多数情况下,点对应问题即会转化为一个优化问题,因此现在问题已转化为求取带权偶图的最大匹配,带权偶图的最大匹配可以用KM(Kuhn-Munkres)算法求解,也可以用文献[7-9]等给出的图匹配算法实现求解。
多数情况下,点对应问题需要求解的是满足一定(最优)条件的完全匹配。本文正是将求解骨-软骨交界面两个点集之间对应问题转化为求解偶图的完全匹配问题。
设A,B分别表示前后两次扫描成像后分割提取的骨-软骨交界面的点集,A={x1,x2,…,xp},B={y1,y2,…,yq}。将A,B作为偶图的顶点,A中每个点与B中每个点均可能存在对应关系,因此A中每个点与B中每个点之间均可以连线作为偶图的边,这样所得到的偶图为完全偶图G=(A∪B,E)。现在需要求解满足一定条件的完全匹配。
首先利用偶图匹配解决完全匹配的存在性问题。
定理1Hall定理设G=(V1∪V2,E)是一个偶图,则|V1|≤|V2|。G中存在从V1到V2的完全匹配充分必要条件是V1中任意n个顶点(n=1,2,……,|V1|)至少与V2中n个顶点相连接。
不难验证,完全偶图符合Hall定理条件,因此完全匹配肯定存在。在此,求解满足一定条件的完全匹配,继续将该问题转化为如下的优化问题:
(3)
(4)
(5)
pij=1 orpij=0
(6)
其中,cij表示xi与yj之间的某种度量(如距离),约束条件(4)要求yj有且只有一个xi与之对应;约束条件(5)要求xi有且只有一个yj与之对应。满足条件(4)、(5)、(6)的解pij可以写成矩阵形式,该矩阵就是前面提到的配置矩阵。
上述优化问题实质上可以视为整数规划或0-1规划中分派问题或指派问题的数学模型,用Munkres分配算法来设计研究求解[10-11]。
2 点对应算法
设A,B分别为Rn的2个集合,A={x1,x2, …,xp},B={y1,y2, …,yq}。用Munkres分配算法求解点集A与点集B之间的对应的步骤如下:
(1)计算距离矩阵D
(7)
如果p≠q,则要通过额外增加行或列的方式保证矩阵D是一个方形矩阵。一般情况下,额外增加行或列的每个元素的值取矩阵D中最大值。
(2)矩阵D中的每一行均减去该行的最小元素。
(3)在第(2)步的基础上,再考虑矩阵每一列,对没有零元素的列,减去该列的最小元素。
(4)用直线覆盖零元素。用最少的直线覆盖所有零元素的所在的行和列,如果所用最少直线条数等于矩阵的行数,则跳至第(8)步。
(5)在第(3)步得到的矩阵中,求取未被覆盖元素的最小元素,然后将最小元素加至每一个覆盖元素上。如果一个元素被覆盖两次(即有横竖两条直线覆盖元素),则该元素加两次最小元素。
(6)考虑第(5)步得到的矩阵。矩阵的所有元素均减去最小元素(仍为第(5)步所求的未被覆盖元素的最小元素)。
(7)再次用最少的直线覆盖零元素。如果所用最少直线条数小于矩阵的行数,则跳至第(5)步。
(8)每行或每列仅选一个零元素。然后在矩阵中将选中的零元素改为1,其它元素都改为0,这样就得到仅含有一个元素的0、1矩阵。
(9)考虑第(8)步所得的元素0、1的矩阵。从矩阵中删除第(1)步所添加的空行或空列,这样就得到了点集A和B之间的对应矩阵M,其中M是一个p×q矩阵。最后,点集A中的点xi通过公式(8)在B中找到与之对应的元素。具体公式表述如下:
(x1,x2, …,xp)=(y1,y2, …,yq)MT
(8)
本文求解点之间的对应方法可阐释解析为如下两步:
(1)对点集A与B实施主轴变换,得到新的点集A′与B′。
(2)对点集A′与B′,使用Munkres分配算法求解点之间的对应。
3 实验结果与分析
为了评估研究提出的点对应算法的性能,本文采用30个猪腿骨和30名膝关节炎患者的MR图像数据。每个猪腿骨数据有18个标记点,每个膝关节数据都有8个标记点,并均将用于算法性能评估。
3.1 MR图像数据获取
将30个新鲜冷冻的猪腿骨MR图像作为实验数据。对于每个猪腿骨,20~22根直径为0.2 mm的竹牙签穿过软骨插入股骨表面后进行两次磁共振成像,视像效果如图2所示。在第二次成像前需对猪腿骨重新定位,然后从MR图像中选出15个标记点,如图3所示。标记点使用图形用户界面(GUI)软件来展开选择设计,该软件可以将MR图像的矢状面、轴状面和冠状面直观呈现在显示器上,还具有旋转、平移(上/下/左/右/前/后)、缩小和放大、调整窗口大小等功能。用户可以逐片浏览MR切片,滚动缩小和放大标记。通过使用GUI,每根牙签标记的中心位置得到了最终确定。单人间隔一周重复6次结果取平均,得到每根牙签标记的中心位置的坐标,误差为0.012±0.002 mm。此外,研究选择的标记经过放射科医生的公正确认。

图2猪腿骨
Fig.2Porcineknee
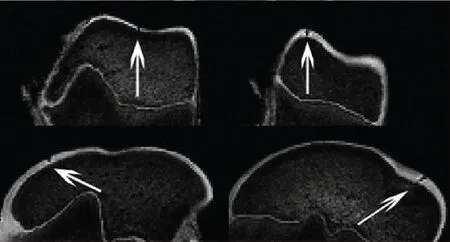
图3 带有标记点的猪腿骨MR图像
30名患者的MR图像数据获取。30名患者信息如下:11名男性,19名女性,年龄范围为32~67岁,平均年龄为52.6岁。每名患者2次扫描成像,中间间隔12个月。使用GUI软件,结合文献[9]方法确定8个标记点的坐标,实际位置即如图4所示。为了使标记点的坐标更趋精确,单人花费2周时间重复6次,结果取平均作为标记点的坐标,误差为0.012±0.002 mm,研究选择的标记也经过放射科医生的公正确认。
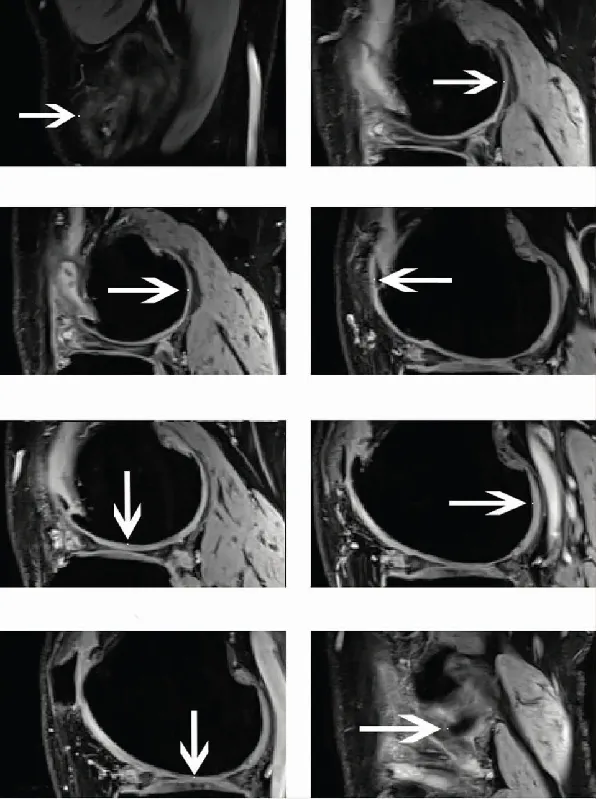
图4 带有标记点的膝关节点MR图像
成像条件:1.5T扫描机(GE Medical Systems,Milwaukee,WI),三维脂肪抑制快速梯度回波(SPGR)成像序列;成像参数:TR/TE=9.0/4.2;flipangle=30°;FOV=320×320 mm;sectionthickness=2 mm;matrix=256×256;scantime=4:30。
3.2 关节软骨的分割
关节软骨的分割主要采用Lynch等提出的一种半自动分割方法[12],下面则针对该方法概述为如下3个步骤,具体内容可参阅文献[12]。
(1)手动初始化。在每张MR图像切片的软骨末端标记两个点,标点位置则详见图5(a);在关节软骨的中心MR图像切片上标记六个点。
(2)检测软骨。计算机优化这些点的位置,将其外推到相邻切片中,详情可见图5(b),并自动调整点使其位于在每个切片的软骨线(cartilage sheet)上,操作效果即如图5(c)所示。接下来,计算机能提供覆盖股骨髁的最佳估计值软骨的3D程度的运算支持,图像输出则如图5(d)所示。在这个过程中,可以人工纠正位置出错的点。
(3)检测软骨内、外交界面。通过人工校正,计算机能调整软骨线至软骨的内边缘(骨与软骨的交界面)和外边缘(软骨与滑膜的交界面),运行结果可如图5(e)所示。
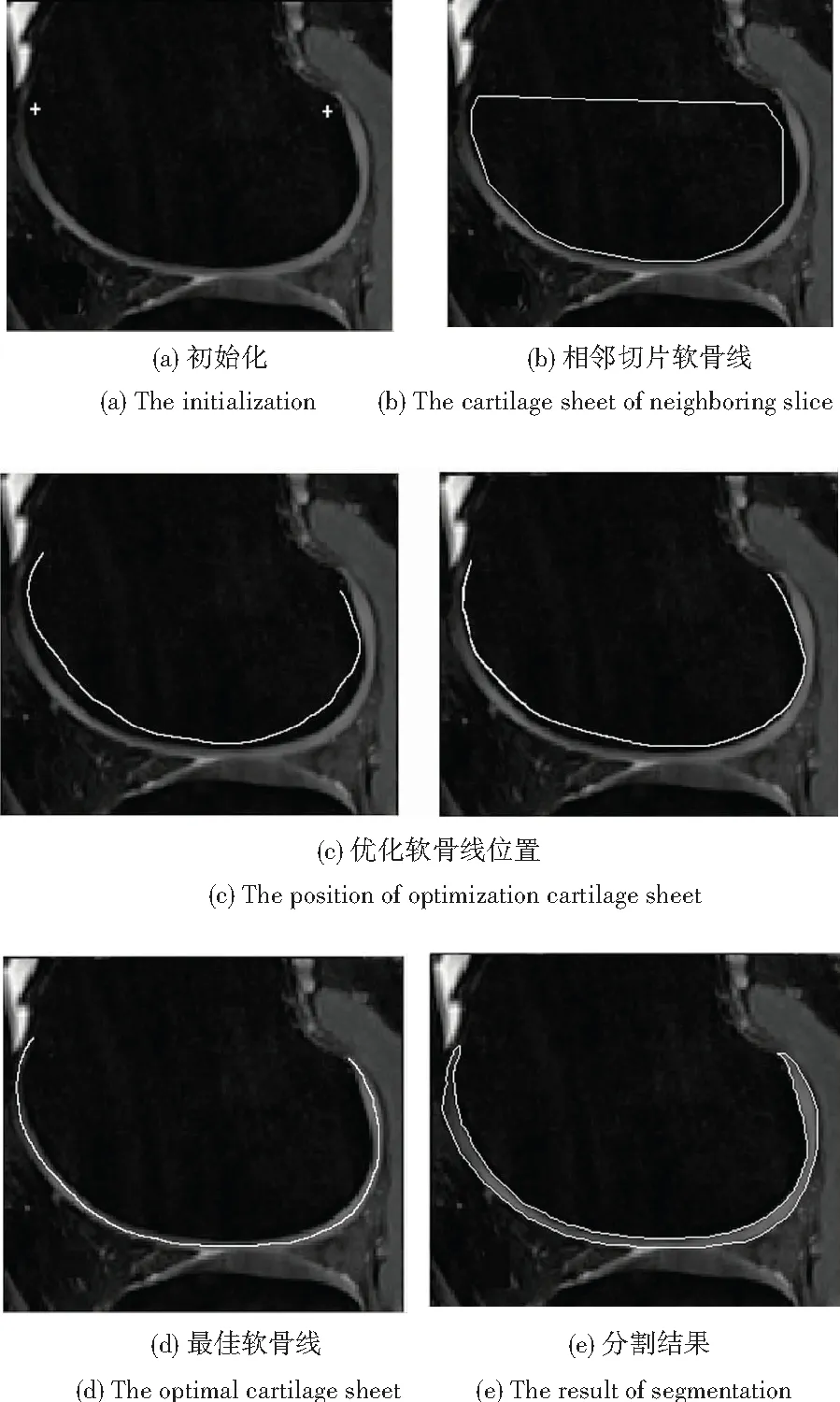
图5 关节软骨的分割
3.3 算法性能的评估
下面将利用上面获取的数据,通过与其它三种求解点对应方法的比较研究来评估本次提出算法的性能。这三种方法分别是:Besl等提出的ICP算法中确定点之间对应的最邻近方法(一个点集中的点与另一个点集中到其距离最近的点相对应[13]);Sanroma等提出的一种用来解决点对应问题的图匹配算法[8];Guo等提出的基于稀疏特性来解决点对应问题的图匹配算法[9]。
对于每个猪腿骨数据,将其第一次扫描成像的MR图像中提取出的18个标记点作为参考点,与第二次扫描成像的MR图像中提取出所有点分别用4种方法进行匹配,这样可以得到18对对应点,然后利用公式(9)计算这些对应点间的欧氏距离之和,然后对30个猪腿骨数据得到的距离之和取平均,可得运算结果如表1所示。
(9)
其中,(xAi,yAi,zAi)(i=1,2,…,18)表示参考点的18个标记点坐标,(xBi,yBi,zBi)(i=1,2,…,18)表示与这18个标记点对应的点坐标。
对于每个膝关节数据进行相似处理,最终可得结果如表1所示。由表1可以看出,本次研究给出方法产生的匹配误差是最低的。

表1 4种方法的匹配误差
4 结束语
为了观测关节炎患者病情变化,本文从MR图像中跟踪关节软骨微小部位的厚度变化来实现研究观测。研究过程可表述如下:通过对关节软骨进行不同时间的扫描,得到MR图像,再对关节软骨进行分割并计算软骨厚度,而后则是计算各对应点之间的软骨厚度差,但前提是必须知道2个软骨点云中各点的对应关系。为此,研究提出了一种解决方法,首先利用一种代数方法使2个点云在空间对齐,然后使用Munkres分配算法求得点之间的对应关系,仿真结果表明研究提出的方法配准误差最低。
