运动模糊图像的恢复方法及其优化

袁江琛

(无锡城市职业技术学院， 江苏 无锡 214153)

引言

生活中由于景物运动，摄像设备的抖动，曝光时间过长等原因，拍摄出的照片会出现模糊现象。如何针对模糊图像进行模糊特征建模以及选择算法，最大程度复原清晰图像是有实际意义的。本文利用运动模糊图像退化及退化模型的建立，重点讨论鉴别线型运动模糊特征的算法，以点扩散函数(PSF)建立模糊模型，以及使用维纳滤波法还原图像。并针对维纳滤波的不足提出可行的改进方法。

1 图像退化及退化模型的建立

1.1 图像退化模型的建立

设原始图像为f(x,y)，摄像机与物体的相对速度为v，曝光时间内相对角位移为θ，g(x,y)为实际拍摄的图像，则有如下关系：

(1)

此处先讨论无角度偏移的情况，则上式可简化为：

(2)

对上式离散化化简，结果为：

g(x,y)=∑f(x-i,y)/L

(3)

式中,L为像素数。此式表明一副模糊图可看成由多幅图像叠加而成。

1.2 点扩散函数的建立

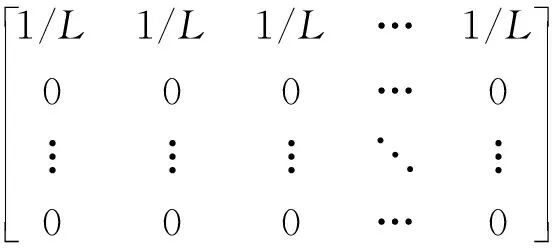
(4)

对以上矩阵进行傅里叶变换得到：

(5)

由上式可看出h(u,v)与v无关，即为在一列中v的值是相同的。令：

(6)

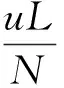
1.3 模糊角度的确定

因为在模糊图像中存在大量的平行于运动角度的直线轨迹，所以只需要对模糊图像进行边缘检测即可快速地估计出运动角度。而边缘检测的基本思想就是针对图像中灰度有跳跃的地方标记出来，这些轨迹就是图像边缘。可使用sobel算子进行边缘检测，sobel算子思想为将两组矩阵与图像作平面卷积，即可分别得出垂直及水平的灰度差分近似值。

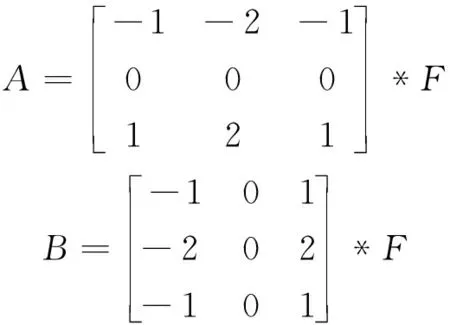
(7)

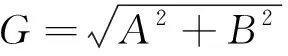
uSobel=imag;

fori= 2:high- 1

forj= 2:width- 1

Gx= (U(i+1,j-1) + 2*U(i+1,j) +F2(i+1,j+1)) - (U(i-1,j-1) + 2*U(i-1,j) +F2(i-1,j+1));

Gy= (U(i-1,j+1) + 2*U(i,j+1) +F2(i+1,j+1)) - (U(i-1,j-1) + 2*U(i,j-1) +F2(i+1,j-1));

uSobel(i,j) =sqrt(Gx^2 +Gy^2);

end

end

根据边缘检测绘制的图像即可简易的确定模糊角度。

2 图像复原

2.1 维纳滤波法

由上述提出的G(u,v)=H(u,v)F(u,v)+N(x,y)函数可知，在忽略噪声因素N的时候，对函数逆向运算反卷积运算即可得到近似的原图。

(8)

但是由上式可以看出，在噪声不能被忽略并且H较小时，噪声会被放大，并且由于H存在零点，在这些点处的图像无法被恢复。从数学上来说，统计误差函数最小时精度最高，统计误差可表示如下：

(9)

则通过化简可以得到：

(10)

从公式中可以看出维纳滤波法引入了Sp(u,v)/Sf(u,v)噪信功率比这项。当噪声为0时维纳滤波与逆向滤波等价，当噪声较大时，通过信噪比抑制复原中对噪声的放大。

由上述证明过程可以看出，维纳滤波法的关键在于反卷积运算。Matlab中自带的deconvwnr函数即部分代码为：

wnr1 = deconvwnr(blurred, PSF2, 0);

subplot(2,3,1),imshow(wnr1);

title('修复图像');

其中，PSF函数即为点扩散函数，Blurred为模糊图像。Matlab中PSF函数有3个参数，分别为模糊类型、模糊尺度和模糊角度。第一个为’motion’类型，即为运动模糊。而后两者的数值就需要根据上文所说的方法进行测定。

2.2 最优窗法优化图像边界

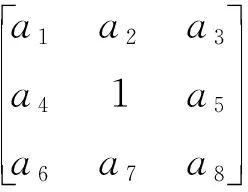
这样在复原的过程中，边缘像素的运算会受到权重的影响，防止了因为像素缺失导致的灰度跳跃。但具体矩阵中的权值大小仍有待探索。

2.3 灰度均衡优化

对于含噪声的图片可以先使用灰度均衡法对图片先行处理。这种改进方法的基本思想是使含有噪点的图片的灰度均匀分布，防止在进行反卷积运算时扩大噪声。

现用r,s表示原始图像和变换后图像的灰度值。0表示为黑，1表示为白。设变换函数为s=T(r)且T(r)有以下特点：

(1)在0

(2)在0

由概率论可知，若图像灰度值的概率密度函数Pr(r)和T(r)已知，则变换后的概率密度函数为：

(11)

由均衡化的定义可知Ps(s)=1，则积分后可得：

(12)

此公式只针对连续灰度的图像。对于离散灰度的图像处理相似。

Matlab中提供了histeq函数进行灰度均衡。但是该函数是针对离散灰度图像的，对于连续灰度的图像处理后视觉上会出现色阶的跳跃。根据上文的转换函数和histeq函数编写了一个新的适用于连续函数的灰度均衡函数，matlab代码如下：

NumPixel=zeros(1,256);

fori= 1:height

forj= 1:width

NumPixel(I(i,j) + 1) =NumPixel(I(i,j) + 1) + 1;

end

end

ProbPixel=zeros(1,256);

fori= 1:256

ProbPixel(i) =NumPixel(i) / (height*width* 1.0);

end

CumuPixel=zeros(1,256);

fori= 1:256

ifi== 1

CumuPixel(i) =ProbPixel(i);

else

CumuPixel(i) =CumuPixel(i- 1) +ProbPixel(i);

end

end

CumuPixel=uint8(255 .*CumuPixel+ 0.5);

fori= 1:height

forj= 1:width

I(i,j) =CumuPixel(I(i,j));

end

end

实验效果如图1所示。

2.4 算法效果

由前文的讨论可知，模糊尺度与模糊角度确定后即可较大程度地复原模糊图像。在图2中利用matlab对一副运动模糊图像的模拟复原。使用前文方法得到原图模糊尺度约为103px，模糊角度为1.5。

3 结束语

本文建立了针对图像的模糊过程的模型和复原过程的模型，也针对图像复原算法的不足进行了优化处理。实验表明，图像复原主要围绕在参数确认和复原滤波两方面。对于参数确认研究希望能找到一种更加精确确认模糊角度的算法，对于复原滤波方面希望能得出更加智能的算法，能自动检测到模糊区域。