一种基于PSO特征加权的局部支持向量机

2018-10-31浩庆波万曙静

智能计算机与应用 2018年6期

浩庆波，高慧，万曙静

(曲阜师范大学网络信息中心，山东济宁 273100)

1 局部支持向量机研究

时下，已有前期文献成果表明，由Vapnik提出的支持向量机(SVM) 在涉及小样本、非线性以及高维分类的研究应用方面有着突出的优势[1]，其基本原理是将样本集中的样本信息通过核函数映射到高维空间中并建立分类超平面，根据分类超平面确定测试样本的类别。支持向量机使用训练样本集中的所有信息(即全局信息)构建分类模型，但这种全局化的思想并不能够体现样本的局部信息。而局部支持向量机则能够有效解决此类问题，充分利用样本的局部信息，满足算法的一致性要求，且其分类精度要高于支持向量机[2]。

局部支持向量机的本质是在支持向量机核函数上添加2个乘子使之具有局部性，模型定义如下：

(1)

核函数的定义如下：

(2)

(3)

这种思想是在样本空间中计算k近邻，却难以适应不同分布的数据集，即数据集不同算法的精度差异将会很大。

接下来，Blanzieri与Melgani则提出了一种新的局部支持向量机(kNNSVM)，测试样本可以通过以下决策函数得到类别标号。该函数的计算公式具体如下：

(4)

kNNSVM使用测试样本x′的k个近邻样本构建分类模型，然后使用SVM算法对样本进行分类。若k的取值与训练集样本数相同，则kNNSVM与SVM算法的分类模型相同。

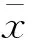
2 粒子群算法研究

粒子群算法是由Eberhart和Kennedy通过研究鸟群捕食行为研发提出的一种群体智能优化算法[3]。粒子群中的粒子定义为一个N维空间的点xi=(xi1,xi2,xi3...,xin)，N维空间就是要优化的解空间，每个粒子都有一个运动速度vi=(vi1,vi2,vi3,...,vin)，粒子在空间内搜索飞行。粒子群算法运行时，将初始化一组随机解，再根据粒子本身的经验以及群体的当前状态更新自身的位置和飞行速度，并借助适应度函数计算得到其适应度值来评价当前解的优劣。粒子群会根据pbest(个体最优解)和gbest(全局最优解)2个极值更新下一代粒子的速度和位置，通过不断地迭代寻找最优解。更新下一代粒子速度和位置的数学公式可见如下：

v[]=v[]+c1*rand()*(pbest[]-present[])+c2*rand()*(gbest[]-

present[])present[]=present[]+v[]

(5)

其中，v[]是粒子的速度；present[]是当前粒子的位置；pbest[]是局部最优位置；gbest[]是全局最优位置；rand()是介于(0,1)的随机数；c1、c2是学习因子，c1表示粒子对自身的认知程度，c2表示粒子对群体的认知程度。

3 基于PSO特征加权的局部支持向量机

3.1 局部支持向量机设计解析

局部支持向量机在选取测试样本的k近邻时，通常采用欧式距离，欧式距离的数学表述如下所示：

(6)

其中，Xi表示样本特征向量；n表示样本的特征个数；x1i、x2i表示样本的特征值。

选取k近邻后，局部支持向量机利用选中的近邻样本构造分类器。在构造分类器时，局部支持向量机将样本特征权重设为相同的值，研究推得分类的决策函数可如式(7)所示：

f(x)=W·X+b

(7)

其中，W，b决定分类超平面的位置，X是训练集样本的特征向量。

但在实际问题中，样本的不同特征在分类过程中的重要程度是不同的。解决的方法是给样本的每一个特征赋予不同的权重来体现其在分类过程中的重要程度，将特征权重作为分类依据参与局部支持向量机的分类，在计算k近邻、分类超平面和核函数时引入特征权重的信息，在公式(6)的基础上加入特征的权重信息，变换后的公式可表示如下：

(8)

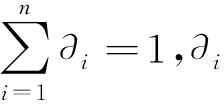
在局部支持向量机的决策函数中加入特征的权重信息，这样就能够减小与分类弱相关或不相关的属性对计算分类超平面的影响，加入特征权重信息的计算公式为:

f(x)=W·(XA)+b

(9)

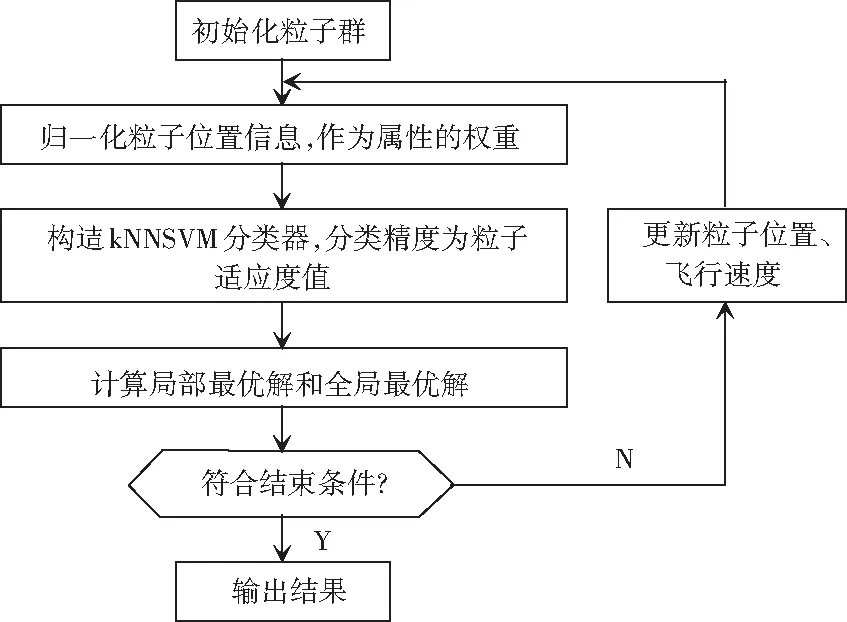
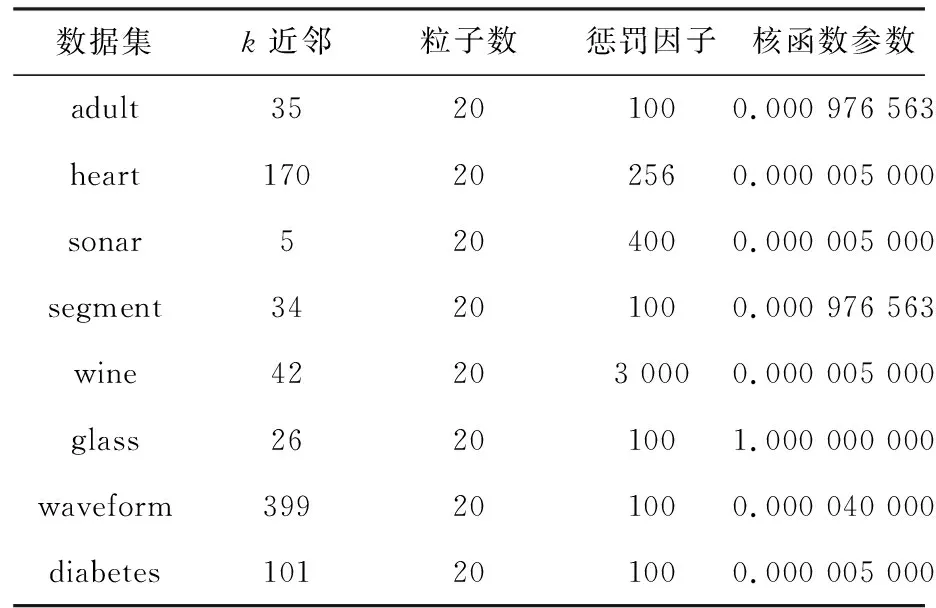
其中，A是一个n阶的对角矩阵，n为样本特征的个数，此时的Aii=∂i(1

(10)

核函数是影响局部支持向量机分类的关键因素[4]。而核函数是根据样本的特征进行计算的，计算过程中核函数会将样本的特征权重设为相同值，这样就会造成分类精度降低，因此研究中引入了特征加权的核函数，即：

kp(xi,xj)=k(xiA,xjA)

(11)

3.2 粒子群算法设计解析

粒子群是利用群体中的粒子信息共享、协作，从而在问题求解空间寻求最优解，获得最优的位置信息。研究中将每个粒子的位置信息归一化后作为样本的初始特征权重，参与局部支持向量机分类器的构造，通过粒子群的迭代过程计算出最优的特征权重组合。

粒子群算法中的适应度函数是根据问题环境而设定的。本文提出的算法是以提高分类精度为目的，因此算法的分类精度即是粒子群的适应度值。

粒子群中的粒子是用一个n维向量p来表示，n表示样本的特征个数，向量p需经过归一化处理，以便提高分类精度。本文中，粒子位置的取值范围为[0，3]，若超过上限则取3，超过下限则取0。

3.3 基于PSO特征加权的局部支持向量机算法研发描述

至此，研究得到的基于PSO特征加权的局部支持向量机算法的设计流程如图1所示。该算法的总体实现步骤可分述如下。

(1) 对粒子群中的每个粒子的原始位置和运动速度进行初始化。

(2) 将每个粒子的位置信息进行备份，并将备份的粒子位置信息在归一化处理后作为分类的权重。使用局部支持向量机对样本(包含权重等信息)进行分类。

(3) 将分类精度作为粒子适应度值求得pbest、gbest的值。

(4) 计算并更新粒子群中粒子的速度。

(5) 在原有的位置信息基础上更新粒子的位置。

(6) 判断算法是否满足结束条件(迭代次数≥N)，若满足则输出分类精度。否则继续执行步骤(2)。

图1 基于PSO特征加权的局部支持向量机

Fig.1LocalSupportVectorMachinesbasedonPSOfeatureweighting

4 实验结果及分析

为验证算法的有效性，本文选取了国际标准UCI数据集进行测试。随机选取数据集中部分数据作为测试集，剩余数据作为训练集，详见表1。

实验将基于PSO特征加权的局部支持向量机(PSOkNNSVM)、支持向量机(SVM)和局部支持向量机(kNNSVM)3种算法用于相同的数据集进行测试。测试采用RBF核函数，相关参数见表2，测试结果见表3，将结果绘制成折线图，最终结果如图2所示。

表1 UCI测试数据集

表2 参数设置

表3 测试结果

图2 分类精度折线图

由表3和图2的实验结果可以看出，SVM在分类精度上小于kNNSVM和PSOkNNSVM。由图2分析可知，在大部分的数据集上，PSOkNNSVM的分类精度要高于kNNSVM。需要指出，在wine数据集上PSOkNNSVM与kNNSVM的分类精度是相同的，究其原因在于wine数据集中样本的每个特征与分类相关程度基本相同，利用粒子群进行优化时最终得到的特征权重也是相同的，与kNNSVM相比特征权重没有变化，故而其分类精度并未获得提升。从其它7个数据集中可以推出在分类精度上，kNNSVM的分类精度要优于SVM，而本文提出的PSOkNNSVM分类精度则要高于kNNSVM和SVM。