基于改进加权移动平均法的服装销售预测

陈银光， 于守健

(东华大学 计算机科学与技术学院， 上海 201620)

引言

预测是对未来将要发生的事情做出的推测。随着数据预测技术的发展，数据预测技术的应用范围日趋广泛，已拓展普及至经济、环境、教育、交通、医疗等重要领域。本文主要研究服装销售相关的预测。时下的服装业正锐意前行，竞争相对也在加剧，因而需要在学习中探索利用科学的方法解决服装销售中的问题，从而增强自身的竞争实力。在服装销售中如果能够预测服装的销售量，不仅有利于合理制定销售计划、最佳优化商品分配、科学控制商品生产、有效避免商品积压，而且可以大幅减少人力物力，由此提高商品销售利润。所以服装销售行业亟需一个快速优质的方法用于服装销售的评估预测，通过选择合适的数据预测模型，结合历史销售数据来预测未来一段时间的销售状况，预测的结果可以辅助企业汇总筹划日常决策，从而发挥一定的参考借鉴作用。

销售数据是典型的时间序列。在基于时间序列的预测分析方法中，移动平均法业已跻身学界流行行列，但也存在一些不足。简单的移动平均法并未考虑周期内数据的权重，加权移动平均法弥补了这一缺陷，但李云刚经过对比证明却发现加权移动平均法也表现出一定劣势[1]。基于此，本文探讨了移动平均法和加权移动平均法存在的问题，通过计算相邻数据的增减情况，引入了趋势的概念，并且利用对整体预测结果的平移处理，解决了预测延迟的问题。而且通过计算误差对比实验可以看出改进后的方法大大提高了预测的精度。

1 移动平均法研究

移动平均法是时间序列模型中比较常见的方法，是一种简单平滑预测技术。该技术的基本原理是根据已知一段时间的数据，从开始位置逐步向后移动指定期数，再求取其平均值作为下一个期数要预测的值。时间序列的数据一般会受周期变动和随机波动的影响，有较大的起伏，不易探寻出时间的发展趋势，使用移动平均法可以消除这些因素的影响，研究求出时间的发展方向与趋势，并据此分析预测未来的发展趋势。

移动平均法可以分为：简单移动平均法和加权移动平均法，本文将对其展开解析分述如下[2]。

1.1 简单移动平均法

设有一段时间序列x1,x2,x3,…,xm，可以参照各数据点的顺序逐点推移求出n个数的平均数，即可得到一次移动平均数，计算公式如下：

(1)

其中，k>n;n为数据移动的周期数，n的值可以结合实际情况设置；xk表示周期内的一次移动平均数，可以依次求出其它的预测值；xk-1,xk-2,…,xk-n为居于xk之前的一个周期的数据。

当k值不断向后推移，移动一次就可以求出一个平均值，这个方法可以依次求出后面一段时间的值。考虑到该方法的设计原理是不断地逐期向后移动，因此将其称为移动平均法。

1.2 加权移动平均法

与移动平均法不同，加权移动平均法就是每一项中均增加了一个权值，具体就是给一定周期的变量值增加不同的权值。其设计原理是基于在一个时间序列中每一个时期的数据对未来预测的作用大小各有不同，因此可为其增加一个权值来衡定其作用大小。分析可知，在一个周期中距离预测时间越远，其影响力就相对较小，而距离越近影响力可能就越大。研究中设置的权重可依从时间的顺序逐渐变大。当周期为n时，加权移动平均法的公式可以表示如下：

(2)

进一步地，式(2)可以简化为：

(3)

其中，w1+w2+…+wn=1；x′k表示预测值；wi表示xk-i的权重，i=1,2,3…,n。

从以上的加权移动平均法公式可以看出，权重的选择是一个关键问题。常规方法是根据经验进行选择。一般情况下，研究中是将距离预测时间近的值赋予大的权重，距离远的将赋予较小权重值。

2 加权移动平均法的改进

在时间序列数据中会存在数值的增加或者减少，移动平均法及加权移动平均法中均未对此予以特别关注，为此研究中将引入趋势的概念[3-5]。在移动平均法中还存在预测结果时间推移的现象，这里通过把预测的结果整体前移一个时间单位用于应对这一问题状况。为此，研究推得改进后的公式可表述如下：

(4)

其中，pk表示预测值；xk+1表示时间序列数据的移动平均值，其求解过程如式(1)所示；x′k+1表示时间序列数据的加权移动平均值，其求解过程如式(2)所示；y表示在n周期内曲线的整体趋势，当y>0，说明曲线整体为上升的趋势。如果y<0，则表示曲线整体呈下降的趋势。y的表达式可以用以下方法进行表示：

(5)

其中，vi表示相邻2个数差的权值。

在前文研究论述基础上，分析归纳后得出改进的加权移动平均法的设计步骤可阐释解析如下。

Step1根据时间序列数据求出周期为n的数据移动平均值，数学运算如式(1)所示。

Step2求取周期为n的时间序列数据的加权移动平均值，数学运算如式(2)所示。

Step3根据式(5)可求得取周期为n的时间序列的趋势平均值。

Step4综合前述3步得到的各方法结果进行合并计算，其数学运算形式即如式(4)所示。

3 实验结果对比

3.1 实验设置

实验数据选取了某一服装销售商2013年12月至2018年5月的销售额，通过使用移动平均法(公式(1))、加权移动平均法(公式(2))以及改进的加权移动平均法(公式(4))进行预测，而这里的预测设计则将以折线图的形式绘制出预测数据与原始数据，从而得到更加直观的误差对比结果。为此，研究中专门选用了平均绝对误差(MAE)和均方根误差(RMSE)用于误差值计算[6]。文中，将对这2个误差计算方法做出研究简述如下。

(1)平均绝对误差(Mean Absolute Deviation，MAE)。MAE是绝对误差的平均值，能够更好地反映预测值误差的实际情况。计算公式如下：

(6)

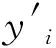
(2)均方根误差(root-mean-square error，RMSE)，也称为标准误差。是观测值与真值偏差的平方与周期次数比值的平方根。RMSE可用于衡量预测值与实际值的偏差。计算公式如下：

(7)

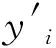
3.2 实验结果分析

本次实验数据中，将移动周期选为3个月，研究拟预测2018年6～8月的销售额。首先使用移动平均法(公式(1))与加权移动平均法(公式(2))进行服装销售额预测，预测的结果与原始数据的对比折线图，则如图1所示。由图1可以发现，传统的移动平均法和加权移动平均法的预测值与实际值之间误差较大。

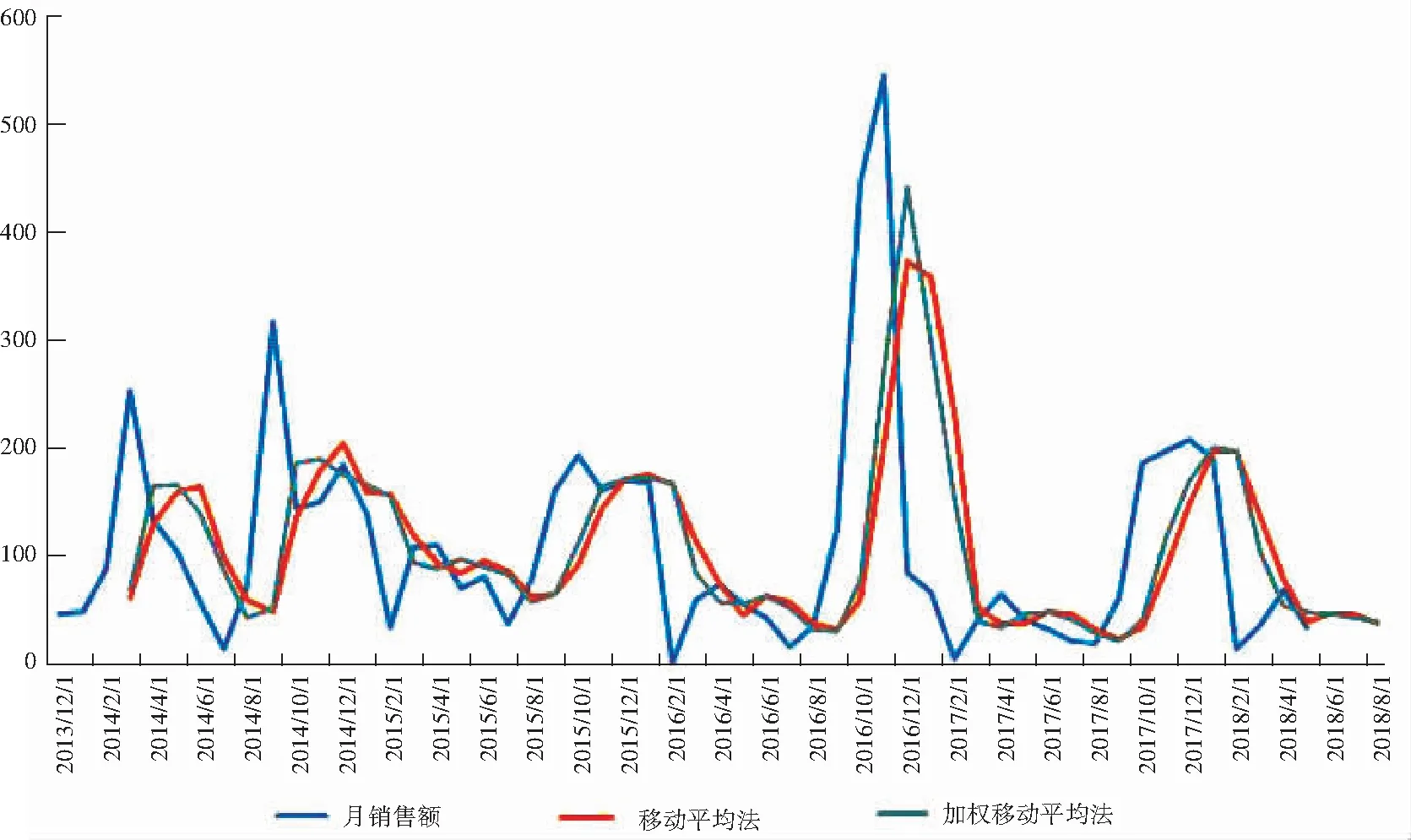
图1 移动平均法和加权移动平均法预测值对比

其次，通过改进加权移动平均法(公式(4))对原始数据进行预测求得的结果与原始数据对比绘制的折线图，如图2所示。其中，服装销售数据移动的周期仍然为3个月，预测2018年6～8月的销售额。通过折线图可以看出，改进后的预测方法与实际数据的误差呈明显减少态势，分析得知改进的加权移动平均法对服装销售额的预测获得了更好的改良性能。

为了更清晰地对比这3种方法的运行结果，使用平均绝对误差(公式(6))和均方根误差(公式(7))计算各类方法误差，运算结果可见表1。通过数值对比可以看到，改进后的方法误差降低了很多，由此即可推得：改进后的加权移动平均法对服装销售额的预测精度有了可观的改善。

根据服装销售商的历史销售记录，分别使用这3种方法预测了2018年6～8月的销售额，预测结果可详见表2。研究至此可知，通过前文的仿真实验证明改进的加权移动平均法在数据预测精度上已有可观改善，因此2018年6月、7月、8月的预测值将可分别选择为：39.83万元、38.97万元、39.07万元。

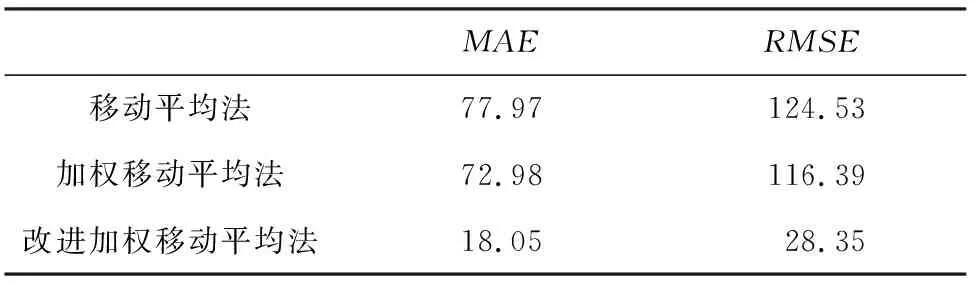
表1 3种预测方法的误差对比

表23种方法分别预测6～8月的销售额

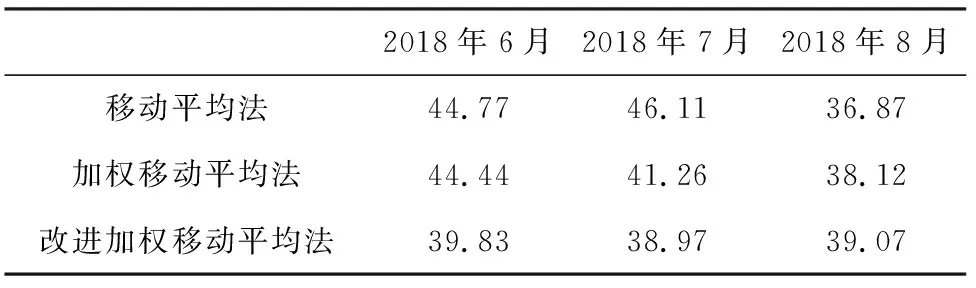
Tab. 2 Three methods predict sales from June to August 万元

图2 改进加权移动平均法预测值

4 结束语

本文在移动平均法和加权移动平均法的基础上，增加了趋势和解决预测推移的方法，构造了一种改进的加权移动平均方法，通过平均绝对误差和均方根误差进行误差分析，经过仿真可以确知：这种改进的加权移动平均法比原有的移动平均预测方法已取得了长足进步。利用这种方法对某服装销售商的未来销售额进行预测，目前虽然仍还存在一些误差，但相对于传统预测方法已有较大的优化与改进。