基于奇部Gabor滤波器的纱管余纱量检测
2018-10-30刘基宏
高 畅, 刘基宏
(生态纺织教育部重点实验室(江南大学), 江苏 无锡 214122)
纱管分拣是细络联设备的一项重要功能,由于从络筒机上退下的纱管可能出现未完全退纱的情况,因此,需要对余纱量进行检测并根据结果分拣纱管。当前装配了细络联装置的自动络筒机普遍采用机械式检测装置,通过各种形式的打手触碰纱管来判定纱管的剩余纱量。这类方案的弊端是打手快速下落和打击纱管表面纱线时,可能会对纱管成形和纱线品质造成不利影响。
近年来出现了非接触式余纱量检测方法,主要通过颜色传感器或相机检测纱管颜色实现数据采集[1],处理方法包括将同类型的空管作为预设值进行比对,或者利用支持向量机或神经网络对颜色进行划分来提取纱线区域[2-3]。这些方案比较依赖纱管和纱线之间的色差,二者颜色相近时易误检,对包缠极少量纱线的残纱管检测效果也不理想。
为提高检测精度,本文提出基于Gabor滤波器的非接触式纱管余纱量检测算法。Gabor滤波器具有带通性和方向性,在边缘检测[4]、纹理分割[5]、疵点检测[6-8]等领域已广泛应用。综合考虑纱管和纱线的色差以及表面纹理差异,本文利用Gabor滤波器奇部反向对称性,设计经过参数优化的多方向多尺度滤波器组对二维图像信号进行过滤,提取包缠纱线部分的边缘,计算纱管余纱量。
1 实验装置
图像采集系统包括CMLN-13S2C-CS型相机、(NanGuang CN-Lux560 LED)光源、遮光板等。相机曝光值为1/60 s,感光度为64,镜头高度与纱管中部平齐且可捕捉到整只纱管。纱管后方用黑色面板遮挡,光源色温为5 600 K。选用高度为 210 mm塑料壁细纱管(有金属底座),卷绕18.2 tex棉纱,纱管固定在底座上,通过由步进电动机驱动的传送带送入画面以模拟实际场景。实验平台系统示意图如图1所示。利用OpenCV编写用于图像处理和输出响应测试的程序。

图1 图像采集装置示意图Fig.1 Diagram of image acquisition device
2 检测算法
系统采样区被限定在背景面板有效遮挡的区域内,检测到有纱管进入后,对图像进行裁剪、阈值分割以及倾斜角度校正,在图像中将纱管矫正至竖直形态;随后用纱管主干区域提取方法将图像缩减至一个仅包含纱管和纱线的矩形;利用极大响应的奇部 Gabor 滤波器滤波,提取管壁上绕纱部分的边缘;最后根据各个边缘之间的距离确定余纱量,为纱管分拣提供依据。算法流程如图2所示。

图2 检测算法流程图Fig.2 Flow chart of detection algorithm
2.1 图像采集与分割
受纱管从络筒机各个锭位退出时间、纱管分拣耗时等因素影响,细络联设备分拣装置处经常会出现纱管排队等待或无纱管的情形。实验装置对此类情形进行了模拟,将检测场景分为无纱管、单纱管和多纱管3种,并采用队列数据结构存储纱管信息;系统对相机拍摄的每一帧画面进行裁剪,去除纱管底座,随后进行固定阈值分割:如果没有检测到足够大的前景连通域,说明没有纱管;如果检测到1个或多个前景连通域,则按其进入检测区顺序编入队列,逐一进行余纱量检测。
每个连通域检测完成后被标记为已处理状态,并且不再在后续画面中被重复检测。当1个纱管离开检测区后,队列中相应的数据和存储空间也被释放,以供后续纱管使用。图3为上述流程示意图。
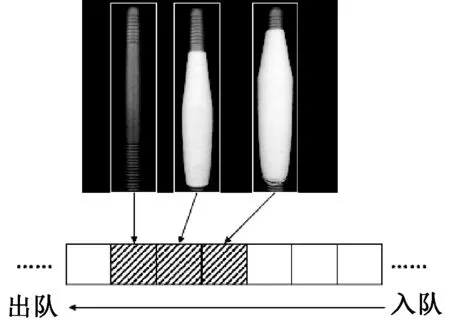
图3 多纱管图像的分割与数据存储Fig.3 Segmentation and data storage of bobbins
2.2 提取纱管主干区域
经过分割后的图像每个连通域内包含1个纱管。纱管在运动状态下自身可能未保持竖直,采用最小二乘法求解线性回归方程,获取管纱倾斜角度[9]。斜率k计算公式为
(1)

取分割图中全部前景点的坐标值代入公式,计算拟合直线斜率。将直线斜率转换为角度后旋转整个分割图,从而将纱管调整至平直状态。
为提高滤波效率,需进一步缩减校正后的图像,将感兴趣区域限定为纱管主干区域,即包含纱管管体、高度略小于纱管高度、宽度略小于纱管直径的矩形。图4示出图像中前景点分布曲线。通过对前景区域的逐列扫描可知:管体覆盖的各列前景点占比较高;而纱线部分呈现梭形,宽度超出纱管直径部分的像素点集在其所在列占比迅速降低。基于这一变化,对图像各列前景点占比设定阈值,高于阈值即视为纱管主干区域。实验中阈值设置为 0.9。
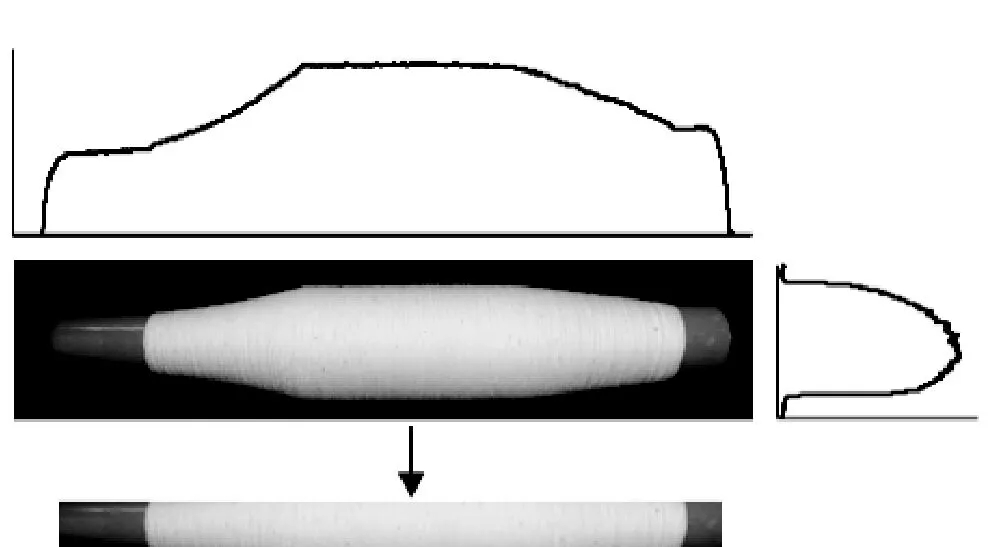
图4 前景点分布统计与主干提取Fig.4 Distribution of foreground pixels and extraction
2.3 奇部Gabor滤波提取纱线边缘
二维奇部Gabor滤波器的定义为
(2)
式中:G为滤波器函数;(x,y)为点坐标;σ2为高斯分布方差;ω为中心频率;ψ为正弦函数相位;γ为二维高斯函数空间纵横比。二维滤波器具有方向性,(x,y)通常表示旋转后的转化坐标,因此还需引入角度参数θ。一般令γ=1,ψ=0是较为合理的滤波器参数设置[5],因此将公式简化为
(3)
式(3)是具有高斯分布加权的正弦平面波,其对轴线x=0处的梯度变化形边缘具有良好的响应效果。二维奇部Gabor滤波器的波形和输出响应随σ(高斯分布标准差)、ω和θ的变化而改变,结合其带通特性,需根据细度大小采用多中心频率和多方向的滤波器组处理输入信号,使得滤波器对纱线边缘产生较大响应,同时抑制其他纹理。
σ和ω决定了奇部Gabor滤波器的波形,二者乘积不变时,中心频率大小仅会影响有效响应区域面积,而波形保持不变。图像中单根纱线的细度在3~6像素之间波动。综合上述因素,设计了由中心频率相同的滤波器构成滤波器组,每组内包含不同方向滤波器。实验中设置σω为1.3,角度选取±90°,组数设置为3,中心频率分别选择2.4、3.4和4.8。
滤波器组对RGB各通道分量分别作卷积,同一中心频率不同方向取极大值,不同中心频率间取极小值,构成滤波输出。滤波器处理效果如图5所示,滤波器经参数优化后可抑制管壁纹理,同时增强纱线灰度梯度。

图5 不同余纱量纱管滤波检测Fig.5 Inspection of bobbins of different remaining amount of yarn. (a) Main part of bobbins; (b) Filtering; (c) Inspecting
2.4 余纱量检测
纱管上的纱线呈缠绕形态,其滤波响应的连通域能够贯穿图像,利用这一特点可提取出绕纱部分。对各通道做最大类间方差阈值分割,如果为前景点则对其进行连通域查找,若其连通域边界达到另一侧边缘列则认定为纱线响应区域;之后合并三通道连通域,若2个连通域距离小于3σ则合并为1个。在获取的响应区域中取相距最远的2组,二者之间区域即认定为缠绕纱线区域。定义纱管余纱量为H,其计算公式为
H=N/w
(4)
式中:N为缠绕纱线区域像素总数;w为纱管主干区域宽度。H代表了缠绕纱线区域的高度,H=0时管纱被判定为空管,H>0时可根据其大小进一步将管纱归类为残纱管、半满管或满管。图5(c)示出余纱量检测结果。可以看出,算法对不同余纱量纱管均可做出准确检测。
3 参数讨论
3.1 纱管主干区域阈值设定
为确定最佳阈值,选取了各种颜色和余纱量纱管图像共计189张,分别记录选取不同阈值处理后提取区域面积的变异系数、提取区域滤波运算速度和检测正确率,测试结果如表1所示。

表1 主干区域阈值测试Tab.1 Test of threshold for main part detection
纱管主干区域阈值决定了滤波图像大小:阈值过高时,裁剪区域面积变化幅度大,检测鲁棒性差,纱管主干区域结果易受噪声干扰;阈值过低会降低运行效率,同时裁剪区域过宽会导致背景点进入选区,误检数大幅提高。综合考虑正确率与滤波稳定性,阈值设置为0.85或0.9较为合理。
3.2 滤波器波形优化
为强化奇部Gabor滤波器的边缘检测效果,需要使其波形在轴线x=0处具有更显著的阶跃特性[10]。这种阶跃也使得滤波器G(x,y)具备更大的输出响应。令E为G(x,y)中心轴线一侧的响应积分:
(5)
对其做积分运算可得:
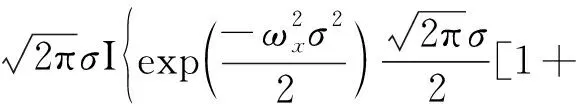
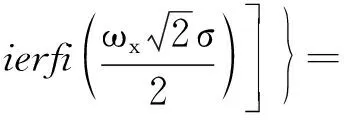
(6)
式中:E表示Dawson积分;I(·)表示取函数虚部;ierfi(·)表示误差函数。式(5)说明若σ已知,则E随ω呈现Dawson分布。Dawson积分拐点约出现在0.924 14,可知E最大时有:
σ≈1.306 9/ω≈λ/4.808
(7)
图6示出测试图像滤波输出响应随λ/σ的变化曲线。可以看出,实际峰值出现于λ/σ=4.808附近,响应曲线与理论值基本一致。

图6 输出响应随λ/σ变化曲线Fig.6 Response curve based on λ/σ. (a) Original image; (b) Response curve
3.3 滤波器角度选取
图7示出奇部滤波器输出响应随θ的理想变化曲线,当θ=90°时,滤波器取得最大响应。为论证理论结果,选取0°~180°,以30°为间隔,共计7个角度的滤波器对测试图像滤波,其响应输出如图7所示。可见,滤波器轴线与阶跃边缘线重合时为滤波效果最好,对于处于竖直状态的纱管而言,θ取90°和中心对称角度270°,2个角度已足以产生理想的滤波效果,过多不同方向的滤波器将降低运行效率,增加噪声。

图7 输出响应随 θ 变化曲线Fig.7 Response curve of filtering based on θ
3.4 滤波器中心频率选取
将单纱沿长度方向微分,每段均可视为没有弯曲的平直纱段,此时需要考察宽度为d的有限宽度模型的滤波输出响应变化规律。在波形固定的条件下,仅需要考虑σ与d的关系。图8(a)示出了滤波器关于σ/d的理论输出模型,滤波器参数σω=1.306 9,θ=90°。由图可知,中心频率为σ的滤波器的最佳响应宽度为d=σ/0.81。图8(c)示出最适中心频率滤波效果。作为参照,图8(a)中σ过小导致滤波效果不明显,未能检测出纱线;图8(d)中σ过大,滤波器最佳响应宽度超过纱线直径,导致噪声过多。

图8 输出响应随σ/d变化曲线Fig.8 Response curve based on σ/d. (a) Response curve; (b) σ=0.4d; (c) σ=0.81d; (d)σ=1.5d
4 结束语
本文对基于Gabor滤波器的余纱量检测算法进行了深入研究。检测系统将纱管图像采集与处理分离,二者同时进行,互不干扰,保证了系统实时性和稳定性。对滤波器组进行优化设计,通过调整参数使得带通范围内的阶跃梯度幅值最大化,强化对纱线的分割效果。探究对特定宽度问题的最适中心频率,合理设置滤波器组合,去除与纱线方向不一致的滤波器,使噪声得到抑制,提高检测效率。结果表明,算法对不同颜色和亮度的纱管能做出准确检测,其优化策略为非接触式纱管分拣研究提供理论参考。
