基于离散混合入侵杂草优化算法的车辆路径问题研究
2018-10-30郇林
郇 林
(陕西工业职业技术学院 陕西 咸阳 712000)
引言
容量车辆路径问题(capacitated vehicle routing problem,CVRP)最初由 Dantzig G.B.和 Ramser.J.H.在1959年提出[1],很快成为运筹学、组合优化、应用数学、物流和计算机应用等领域的前沿研究课题。研究课题包括食品分销、报纸和邮件投递、废物回收、计费和运输路线规划等等。解决CVRP,可降低物流成本,提高经济效益,改善客户服务质量。另外,CVRP已被证明是NP完全问题。因此,对于CVRP求解算法的研究具有重要的理论、工程和实际意义。
由于CVRP属于NP完全问题,不同学科的专家所提出的主要是精确算法和构造型启发式算法,但是在实际应用中,这2种算法都不能满足解决大规模问题的需求,获得最优解很困难,于是出现了对智能优化算法的研究和开发。Zhao Y.W.等人[2]提出了一种求解CVRP的混合量子进化算法。实验结果表明,混合量子进化算法优于遗传算法和粒子群优化算法。Wang Y.[3]提出了一种混合量子遗传算法用于求解CVRP,利用免疫算子提高算法的局部搜索能力,获得了较好的性能。入侵杂草优化(invasive weed optimization,IWO)算法,首先由 Mehrabian 等人[4]在2006年提出,是一种随机搜索算法。它模拟侵入性杂草的繁殖过程,也就是模拟入侵杂草种子的分散、生长、繁殖和竞争排斥过程。由于IWO具有较强的鲁棒性、适应性和随机性,因此吸引了不同学科(如电气和电子工程、计算机科学、自动控制系统和人工智能等)专家的兴趣和研究。与遗传算法相比,IWO算法在解决复杂问题时更加方便和鲁棒。Ghosh等人[5]提出用IWO解决贝塞尔参数的最优控制问题,可有效降低控制成本。根据上述文献,IWO在解决一些实际工程问题中优于遗传算法和粒子群优化算法等经典算法,但在离散组合优化问题中很少使用。
1 CVRP问题的数学模型
1.1 问题描述
车辆路径问题模型的建立基于以下假设:
1)每个仓库中的车辆属于同一类型(相同的货物),车辆数量因客户需求而异;
2)车辆的负载有限,不能超载;
3)每位客户必须被访问且只能提供一次服务,不允许重复访问;
4)完成车辆配送任务后,车队必须返回原仓库。
基于上述假设,车辆路径问题描述如下:K车辆从一个配送中心开始服务n个顾客,每辆车的负荷极限为Qk(k=1,2,…,K-1,K),每个顾客的需求为qi(i=1,2,…,n-1,n),dij代表顾客i和顾客j之间的距离,d0j代表配送中心和顾客j之间的距离(i,j=1,2,…,n-1,n)[6-9]。
1.2 CVRP问题的数学模型
配送中心容量化车辆路径问题的数学模型如下:
代表车辆最短路径的目标函数由下式表示:
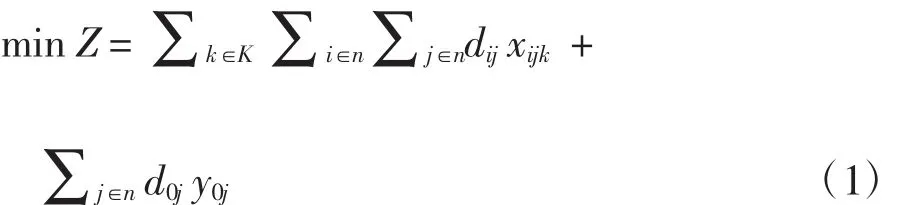
确保每辆车负载约束条件的公式为:

确保每个客户都可以访问的公式为:

确保客户只能得到一次服务的公式为:
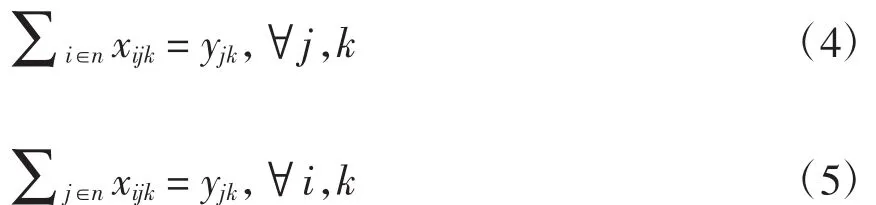
消除子回路,以防止车辆从原始路径或部分路径返回的公式为:

用于确保决策变量范围的公式为:

2 离散混合入侵杂草优化算法
入侵杂草优化算法是一种随机搜索算法,用于模拟入侵杂草克隆的行为。该算法简单,高效,鲁棒,适应性强,随机性强,易于理解和编程。
1)编码。在解决多车路径问题时,总体个体(解决方案)的表示必须能够表示车辆路径。对于有K个分销车辆的 n个客户,人口个体代表(1·(n+k))矩阵,包括2部分:每个客户的服务订单和车辆的订单。
2)复制。杂草的适应性越高,克隆的可能性就越大,产生的种子数量就越多。所以,每种杂草的种子数量计算如下:

式中:floor表示种子四舍五入到最接近的整数;fmax和fmin分别表示最大和最小适应度;fi是第i种杂草的适应度;Smax和Smin分别表示种子数量的最大值和最小值。
公式(10)表示了种子数量与杂草适应度之间的数学关系,种子数量随着适应度的增加而减少,并且种子数量在Smax和Smin之间变化,各元素间的关系如图所示。
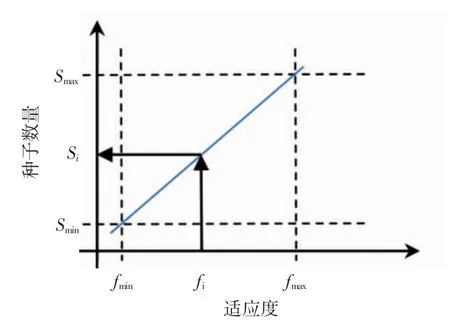
图1 种子数量与适应度的关系
3)空间分配。种子数量范围从Smin到Smax,随机分布在杂草周围的正态分布中,正态分布的标准差可通过以下公式计算:
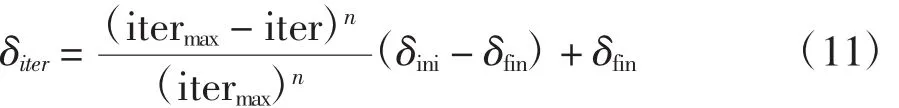
式中:iter为迭代次数;δiter是iter生成的标准偏差;itermax为最大迭代次数;δini和δfin分别为初始和最终标准偏差;n为非线性调制指数。
生成的种子通过随机正态分布函数在解空间上分布,确保搜索过程能在每个杂草的局部区域搜索更好的解决方案,并且IWO的本地搜索能力得到增强。然而,IWO种子扩散具有连续的正态分布,因此,它不能直接作为种子进入下一次迭代,相应的离散处理方程如下:
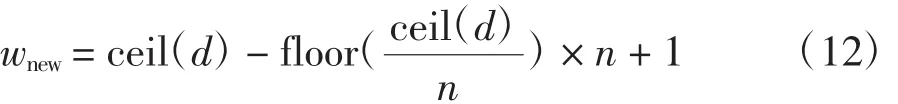
式中:wnew表示种子生成数量,ceil是舍入操作,floor表示wnew可以四舍五入到最接近的整数,n为每个仓库的客户总数(添加1以防止形成0)。
wnew中可能会出现相同的数字,为了防止这个问题出现,使用wnew中的客户序列号来替换wnew中重复的数字;例如,如果父代是 wpa=[2,1,4,3,5],步长为5,N(0,5)产生的5个扩散值分别为d=[-6.037 4,5.862,8.151 2,2.444 5,5.173 4],可通过公式(12)计算出 wnew=[5,5,5,4,2]。可以看出,第 5 位顾客被访问了3次,而第2位和第4位顾客未被访问,所以数字1 和 3 将随机取代一个数字 5,可变更为[1,3,5,4,2]。
4)适应度。由于 VRP(vehicle routing problem,车辆路径问题)被视为最小化问题,其适应度函数流量描述如下:

式中:f(x)为车辆旅行成本的总和。
5)F-自适应方法。F-自适应方法包括自适应交叉和自适应变异。引入F-自适应方法,可保持IWO算法中杂草的多样性。交叉和变异概率根据种群的多样性自适应调整。
6)竞争排斥机制。每次迭代包括3组:初始杂草、育种种子和杂草的进化等,如果不限制杂草的数量,将阻碍IWO的效率,所以必须引入竞争排斥机制,即按照升序的适应度构建大群体。
7)两阶段混合变邻域搜索。使用混合变邻域搜索是增强算法本地搜索能力的重要方法,在最佳解决方案的附近,通常有一个或多个最佳解决方案。本文采用改进的2-Opt方法结合基于位交换操作的变域搜索方法来搜索最优解。在改进解决方案的过程中,2-Opt方法通常用于重新优化车辆路径。基本原则是从现有路径中随机选择一个边界去除,然后重新连接其他2个节点以形成新的路径。作为条件,新路径的长度小于原路径的长度。由于2-Opt在选择边界方面的低效率,推荐使用改进的2-Opt。改进的2-Opt方法的基本步骤如下:
a)随机选择路径。T:v1,v2,...vi,vi+1,vi+2,…vj-1,vj,vj+1,…vn.i≥1,j=i+2;
b)选择路径中的第一条边(vi,vi+1),i=1,2,…,n-2;
c)选择第二条边(vj,vj+1),j=i+2。如果 d(vi,vj+1)+d(vj,vj+1)>d(vi,vj)+d(vi+1,vj+1),则执行改进的 2-Opt。(vi,vj+1)和(vj,vj+1)将被替换为(vi,vj)和(vi+1,vj+1),然后返回步骤 b),或返回步骤 e)。
d)j=j+1。如果 j>n,则返回步骤 e),或返回步骤c)。
e)i=i+1。如果 i<n-1,则返回步骤 b),或终止2-Opt程序。
8)终止标准。上述过程一直持续到达到最大迭代次数为止。
3 离散混合入侵杂草优化算法解决车辆路径问题仿真实验
离散混合入侵杂草优化(discrete mixed invasive weed optimization,DMIWO)算法可以用来求解CVRP的优化问题,并将所得结果与文献中的遗传算法、粒子群算法和量子进化算法进行比较。在具有Windows 7平台和4GB RAM的计算机上使用MATLAB对所有问题进行了仿真实验,验证了DMIWO在求解离散组合优化问题中的有效性、适应性和鲁棒性,通过DMIWO算法,得到3种车辆调度问题的的最优解,3种车辆的最优路径图和收敛图分别如图2和图3所示。

图2 3种车辆的最优路径图

图3 3种车辆的收敛图
4 结论
本文设计了一种离散混合入侵杂草优化(DMI WO)算法来解决不同规模的车辆路径问题。使用实数矩阵进行实数编码,引入遗传自适应变异和自适应交叉,并使用两阶段混合邻域搜索方法确保全局搜索能力和本地搜索能力之间的平衡,以寻求更好的解决方案。仿真实验表明,适用于离散组合优化问题的离散混合入侵杂草优化算法在性能计算、收敛速度和优化效率等方面均有明显优势。
