基于星下点机动的再入飞行器离轨规划
2018-10-30史树峰师鹏赵育善
史树峰, 师鹏, 赵育善
(北京航空航天大学 宇航学院, 北京 100083)
天基全球作战能力是未来航天军事发展的一大方向,受到世界航天强国的普遍重视。此类研究一般以美国提出的通用航空飞行器(CAV)概念为蓝本,重点突出从轨道或亚轨道高度再入大气层对地面目标进行定点打击的能力。CAV的待命轨道高度一般在400~500 km,当攻击任务触发时,飞行器脱离待命平台并启动离轨模块,通过轨道制动脱离原轨道进入返回地球大气层的下降轨道,进而穿过大气层抵达地面目标[1-3]。
再入飞行器离轨过渡轨道的相关研究中,陈洪波和杨涤[4]分析了离轨推力对下降轨道再入角的影响;高浩等[5]解决的主要是拦截时间限制下离轨过渡轨道的优化算法;笔者[6]对离轨过渡段轨道特性进行了分析,提出了离轨参数的规划方法。现有研究着重于离轨过程的性能,缺少对再入点位置精度的考虑。虽然对于具有大气层内机动能力的飞行器来说,其最终飞行落点并不严格受制于再入点位置精度,但精确的再入点参数控制能够有效地增强落点覆盖准确度,减少飞行器待机时间,从而增加任务可靠性。因此本文强化了对再入点位置精度的约束,在飞行器燃料允许的前提下,如果飞行器在当前轨道状态不能准确离轨到预定再入点地理位置,则考虑依据其星下点轨迹进行预先的轨道调整,从而实现再入任务的精确实施。关于星下点轨迹的研究多侧重于遥感卫星的回归轨道或星下点保持[7-9],针对特定地理位置目标的星下点机动研究则较少。研究针对目标星下点轨迹所需的轨道机动,大多利用经验公式[10]、霍曼变轨[11-12]或小推力变轨控制[13]等传统方法给出控制参数,本文结合离轨任务实际情况,提出单脉冲实现的星下点机动方法。
本文研究对象为再入飞行器从潜伏轨道转移到大气层上界(高度为120 km)的再入点之间的离轨段和过渡段轨道,通过对再入飞行器的离轨制动时机和离轨控制参数的规划,实现指定再入点位置的飞行器离轨任务。
首先,对再入飞行器离轨任务特性进行分析,提出了以星下点轨迹为参考对象的直接离轨必要条件;然后,对于满足直接离轨必要条件的情况,完善了固定有限推力模式下最优离轨关键参数的确定方法;最后,针对不满足直接离轨必要条件的离轨任务,提出能使轨道参数符合离轨条件的单脉冲星下点机动方法。
1 离轨制动冲量模型
再入飞行器从离开原停泊轨道返回地球大气层到最终着陆于地球表面的过程可分成4段,即离轨段、过渡段、再入段和着陆段[14],其中前2段在大气层外,是本文的主要研究对象。
图1具体展示了再入飞行器的离轨再入示意图。再入飞行器于原轨道ε1上以速度v1飞行,在离轨点D处离轨任务触发对飞行器施加制动速度Δv,使飞行器的速度变为v2,从原来的轨道进入椭圆过渡段轨道ε2上,过渡段轨道与大气层上界(默认为120 km高度)的交点为飞行器再入点E,此处飞行器有2个特征参数再入速度ve和再入角ϑe,之后飞行器进入再入段轨道。再入点E的位置及其2个特征参数对飞行器返回任务能否成功起到决定性影响[15]。飞行器离轨任务设计的一般内容即为已知初始轨道ε1及再入点E的位置和特征参数,再根据其他限制条件,计算离轨点D的位置及相应的制动速度Δv。
本文研究对象中离轨段轨道有制动推力,过渡段轨道是无动力滑行轨道。图1中O表示地心,ϑ1和ϑ2分别为制动时刻前后飞行器速度相对于当地水平方向的角度。
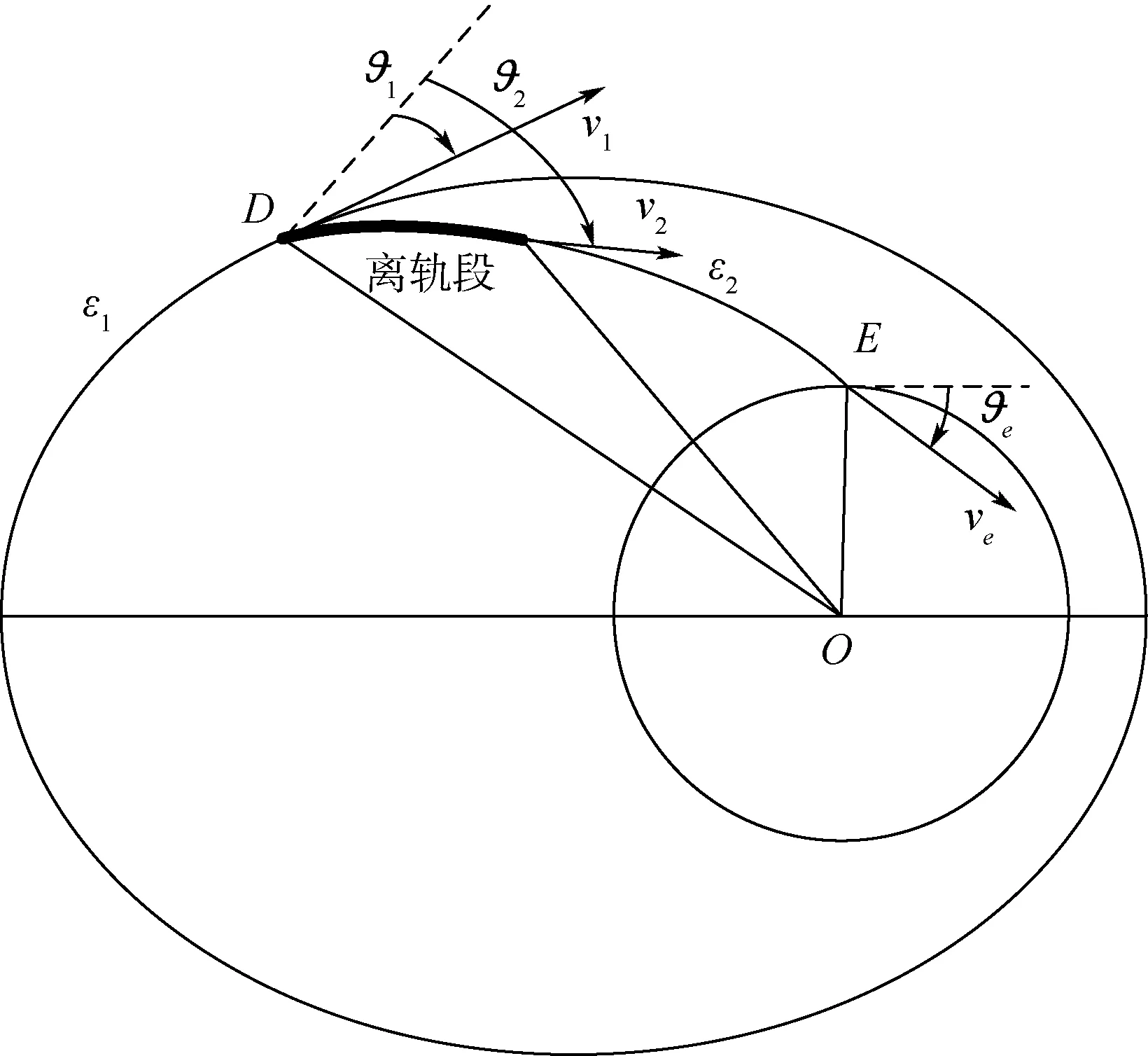
图1 离轨再入过程示意图Fig.1 Schematic of deorbit and reentry process
在再入飞行器离轨规划任务中,初始轨道一般为近地近圆停泊轨道,再入点特征参数一般由具体飞行器在大气层内飞行所需的气动条件预先限定。粗略评估计算中会使用无旋转地球模型,计算结果中只能体现离轨过渡轨道与再入点之间的几何关系;实际在任务中由于涉及了再入点的经纬度位置,需要考虑地球旋转因素进行计算。本文再入飞行器离轨制动规划的任务可以描述成:已知飞行器当前飞行参数,为使飞行器变轨到达指定的再入点经纬度并满足任务要求的再入点特征参数和最优性能指标,规划计算制动点位置和制动推力参数。
离轨过渡轨道与再入点参数间的几何关系可以使用无旋转地球模型和冲量式制动方式建立。一般的椭圆潜伏轨道制动的制动点与再入点关系如图2所示,制动角φ为制动速度Δv与初始速度v1的夹角,且以向下为负值。r1为制动点原轨道地心距,r2为制动后地心距,re为再入点地心距,在冲量假设下制动过程瞬间完成,所以有r1=r2。
文献[6]建立了冲量假设下圆轨道下制动速度参数与再入点参数之间的关系,并推导了最小冲量条件下制动角的计算方法,得到在一般情况下的制动任务中制动发动机的最佳推力方向应在圆轨道运动的反方向。本文任务内容涉及初始轨道为椭圆轨道的情况,因此进一步推导冲量假设下椭圆初始轨道制动速度参数的计算方法。
由轨道力学可知
(1)
(2)
(3)

图2 椭圆轨道制动的制动点与再入点关系Fig.2 Relationship between braking point and reentry point of ellipse orbit braking
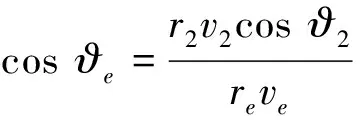
(4)
式中:μ为引力常数。
从式(1)~式(4)可以看出,当已知re、ve和ϑe时,可以由式(1)和式(2)确定Δv和φ的大小。但如果ϑe已经由气动条件决定,且对ve的大小不作要求时,可以求出最佳的φ值使Δv最小。
由几何关系可知
v2cos ϑ2=v1cos ϑ1+Δvcos(φ+ϑ1)
(5)
由式(1)和式(3)可得
(6)
将式(5)和式(6)代入式(4)可得
(7)
对式(7)求导可得
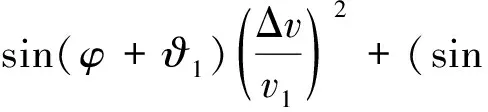
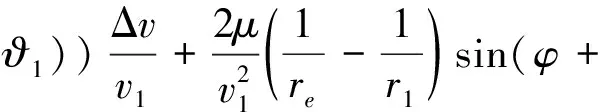
sin ϑ1cosφ=0
(8)
求解式(8)可以得到使Δv/v1最小时,Δv/v1与φ的关系:
(9)
式中:
K1=(sin ϑ1+cosφsin(φ+ϑ1))2-4sin(φ+ϑ1)·
式(9)没有显式解,可使用牛顿迭代法求解,初值猜测可令φ=-π。
2 固定有限推力离轨规划
离轨制动冲量模型使用无旋转地球模型,主要解决离轨脉冲参数与任务给定再入点特征参数之间的关系。实际任务中的任务参数增加了对再入点的维度限制,即限定了再入点在地面上投影的经纬度,因此必须考虑到地球旋转的影响,引入星下点轨迹作为研究对象。直观上看,轨道机动对星下点轨迹的影响如图3所示,原轨道星下点轨迹以S0表示,如果在D点执行不同的轨道机动,星下点轨迹会在东西2个方向上偏离S0,产生2类新轨迹S1和S2,随着时间推移星下点轨迹偏移量会逐渐积累而使新轨迹与原轨迹的区别愈发明显。实际上为了展示图3中的星下点轨迹变化,对其进行了夸张处理,一般任务中的小幅度轨道调整对轨道本身的改变有限,只会对短弧段中的星下点轨迹造成微小改变。离轨过程从离轨点到再入点一般只经过约1/4个轨道弧段,经过计算其间星下点轨迹的变化可以忽略,其中产生的误差可以在离轨参数规划中得到弥补。
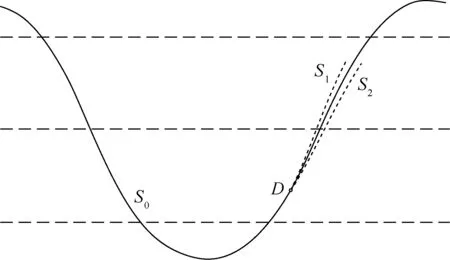
图3 轨道机动对星下点轨迹的影响Fig.3 Influence of orbit maneuver on ground track
因为实际任务增加了对再入点地理经纬度的限定,所以能得到离轨过渡轨道的一项限制条件,即过渡段轨道的星下点应通过再入点地理经纬度。结合对图3的分析,可以得到能通过直接离轨制动使飞行器到达目标再入点位置的近似必要条件,即飞行器原轨道应通过任务指定的再入点地理经纬度。因此离轨规划任务需要解决2个问题:一是满足直接离轨必要条件下对离轨参数的规划问题,二是不满足直接离轨必要条件的处理方法。
首先分析满足直接离轨必要条件下的离轨参数规划问题。离轨过程包括离轨段和过渡段轨道,实际任务执行中离轨段的动力由轨控发动机提供,通常不会是大推力发动机,因此不能直接使用第1节中的冲量模型,而由于离轨所需的轨道机动幅度一般不大,离轨段轨道较短,发动机使用固定大小固定方向的推力模型即可。离轨规划须要调整的参数包括制动点位置(即制动点的经纬度)、发动机推力大小、方向和工作时间。
离轨段轨道使用有限推力下的动力学模型为
(10)
式中:r和v分别为飞行器位置和速度矢量;T为发动机推力;m为再入飞行器的质量;g0为标准重力加速度;Isp为发动机比冲。
文献[6]提出了离轨制动问题的2层规划方法,能解决初始轨道为圆轨道且满足直接离轨必要条件的离轨规划问题,本文对此略作修改,使其适应一般初始轨道的直接离轨规划问题。
离轨参数规划策略如下:
第1层选定初始猜测制动点位置(Bi,λi),通过求解非线性规划问题计算满足再入点约束,且燃料最优的制动角φ,由于采用固定推力模型,燃料最优指标由发动机工作时间tp极小值表示。
轨道参数符合直接离轨条件,因此可以找到原轨道星下点轨迹通过指定再入点经纬度的所在弧段,预估选取初始制动点经纬度(Bi,λi)。对于每个制动点,由制动角φ和工作时间tp决定了离轨段轨道和过渡段轨道,继而与大气层上界(高度为120 km)相交于再入点位置。第1层规划可以描述成带约束的非线性规划问题,即
mintp=f(φ)
(11)
式中:f(φ)为有限推力下离轨制动过程制动参数的隐函数,其中包括式(10)表示的有动力离轨段轨道,还包括自由下降的过渡段轨道;tmax为任务燃料容许的发动机最大开机时间;ϑe0为任务要求的再入点倾角;he为再入点高度。求解非线性规划问题使用了SNOPT非线性规划程序包[16],规划猜测初值选择根据初始轨道类型决定,如果初始轨道为近圆轨道,则选择φ初值为-π,如果初始轨道为椭圆轨道,则根据式(9)计算φ初值。
第2层由于第1层规划仅针对再入点性能参数,其结果是满足再入点倾角约束的最优离轨,但对指定再入点经纬度的任务而言,其结果中的再入点位置与任务要求存在偏差。因此根据第1层选定的制动点(Bi,λi)和制动点参数,计算再入点经纬度误差Δe,通过一维搜索方法寻找制动点在原轨道星下点轨迹上的位置,直到结果中再入点位置收敛到任务要求的经纬度。
离轨制动参数规则流程如图4所示,其中下标j表示第1层规划迭代过程中的参数估计,ε表示再入点经纬度的容许误差。
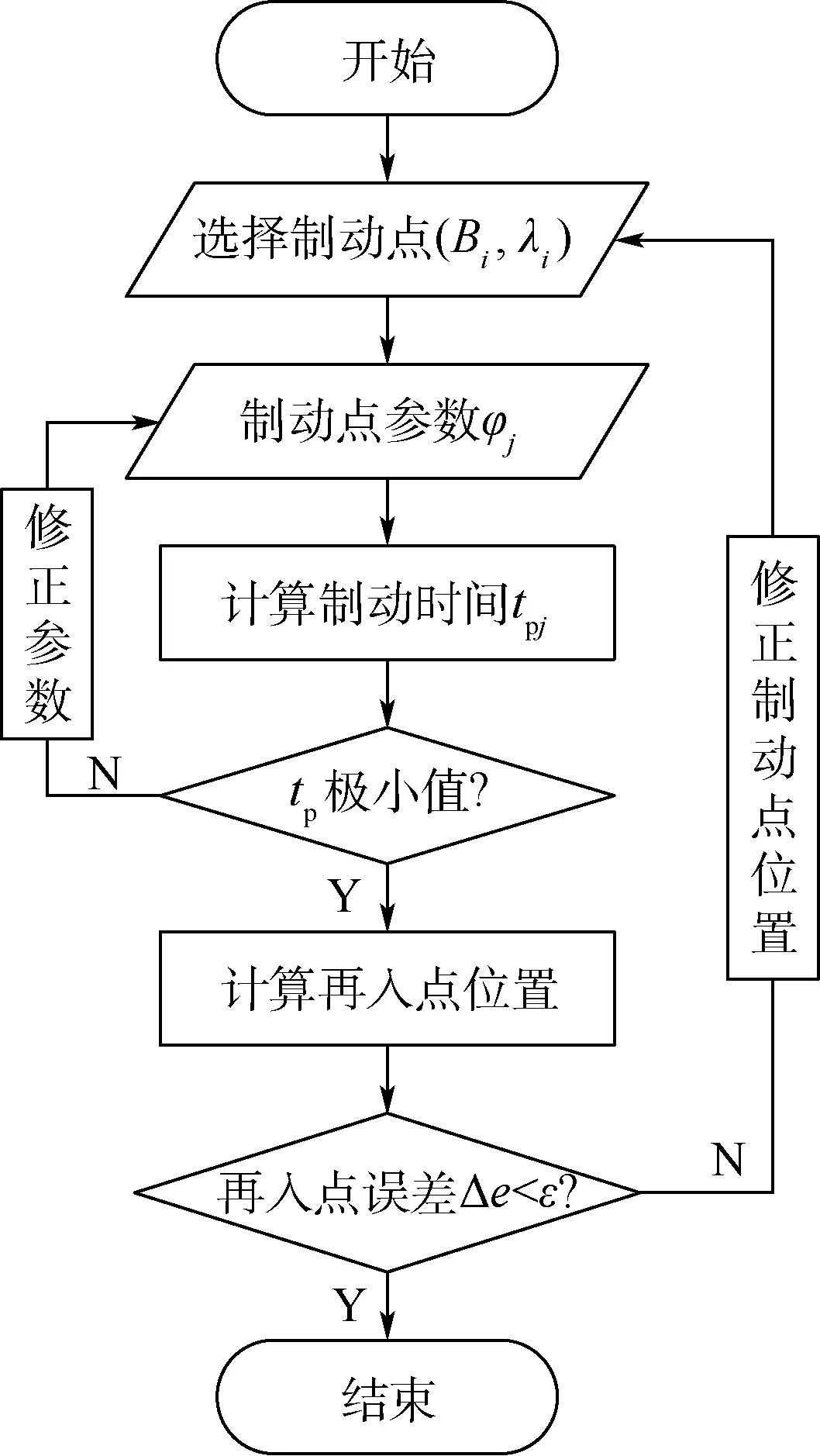
图4 离轨制动参数规划流程Fig.4 Flowchart of deorbit braking parametric programming
3 再入点星下点机动
对于不满足直接离轨必要条件的情况而言,目标再入点位置偏离飞行器原轨道的星下点轨迹,无法直接从原轨道离轨达到目标再入点。因此考虑使飞行器在离轨前预先调整自身轨道,使新轨道星下点轨迹通过目标经纬度。
假设以轨道切向脉冲改变原轨道高度,则轨道周期会相应变化,从而改变目标经纬度附近轨道星下点位置。如果以目标纬度为基准,对原轨道施加正切向脉冲可以使星下点轨迹相对西移,同理施加负切向脉冲可以使星下点轨迹相对东移。因此需要研究改变星下点轨迹所需机动的参数。
假设星下点机动初始时刻为t0,飞行器以上升轨道运行到目标再入点纬度时的赤经为
αt=Ω0+arctan(cositanut)
(12)
式中:Ω0为初始轨道升交点赤经;i为轨道倾角;ut为飞行器从上升段轨道运行至目标纬度时的轨道纬度幅角。
定义飞行器轨道面与目标再入点的经度差值为
Δλ=αt-α0
(13)
式中:α0为初始时刻目标位置的对应赤经。
一方面,以轨道面为参照,由于地球自转和轨道进动,可以认为目标再入点沿着自身纬度线绕轨道面旋转。从初始时刻开始,目标第1次穿过轨道面上升段的时间为
(14)
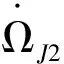
如果整个机动过程更长,那么目标第N次穿过轨道面上升段的时间为
(15)
目标再入点位置每2次穿过轨道面上升段的过程,对应着飞行器星下点轨迹与赤道的交点在赤道面上移动了一周,以时间计约为1 d。tN时刻目标穿过轨道面但不一定落在星下点轨迹上,因此在tN时刻前后必然存在2条上升轨道的星下点轨迹,使目标再入点经纬度落在这2条轨迹之间。
另一方面,飞行器从上升段轨道飞临目标再入点纬度处所需时间为
(16)

那么飞行器星下点第M次从上升轨道穿过目标纬度的时间为
tM=t2+(M-1)TΩM=1,2,…
(17)
式中:TΩ为交点周期,其表达式为
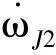
如果对飞行器施加脉冲Δv,存在某个数对(N,M)使得式(15)和式(17)中的tN=tM,则可以判断轨道机动后的星下点轨迹经过了目标再入点经纬度。
具体仿真中,首先需要确定参数N,其决定了轨道调整过程的时间跨度。对于全球定点打击一类的飞行任务,必然要求实施时间尽可能短,因此在恰当选择负责实施任务的再入飞行器情况下,将N值设为1,也就是限定任务在1 d内完成。对于确定的N值,则必然存在2个接近最优的M值可行解,分别对应了原轨道星下点轨迹上,位于目标位置东侧的轨道段,由于施加正切向脉冲而西移的Meast,以及位于目标位置西侧的轨道段,由于施加负切向脉冲而东移的Mwest。即
(18)
式中:⎣」、「⎤分别表示向下、向上取整。而这2个值中必有一个能使Δv取最小值,也就是最省燃料的轨道机动方案。
4 离轨制动规划仿真
以不满足直接离轨必要条件下的仿真案例展示离轨制动规划整体过程。
选择初始轨道的轨道根数如表1所示,表中a、e、i、Ω、ω和f分别表示轨道半径、偏心率、倾角、升交点赤经、近地点幅角和真近点角。任务初始历元为UTC 2016-10-01 20:00:00。飞行器质量为3 000 kg,轨控发动机推力固定为1 175 N,发动机比冲为300 s。
目标再入点参数要求如表2所示。

表1 初始轨道根数
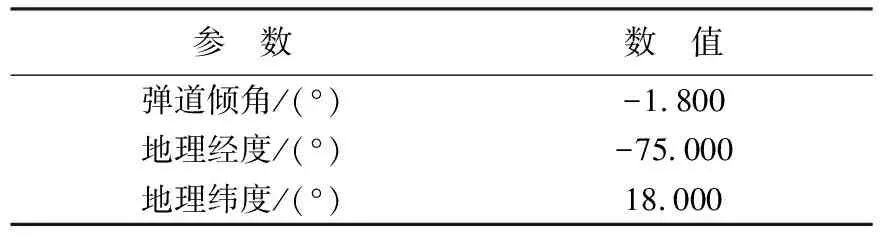
表2 再入点参数

图5 飞行器原轨道的星下点轨迹Fig.5 Ground track of original orbit of vehicle
作为规划计算前的准备,首先生成原轨道在1 d内的星下点轨迹如图5所示。为了使规划计算更为精确,轨道预报中考虑了地球扁率摄动,采用了高阶地球引力场模型。图5中实线表示飞行器星下点轨迹,点划线表示目标再入点所处纬度,实心圆表示任务初始时刻再入飞行器所处位置,星号表示目标再入点的经纬度位置,箭头指示了飞行器运动方向。从图5可看到,再入点位置约处于上升轨道段的第11轨与第12轨的星下点轨迹之间,因此其初始轨道并不符合直接离轨必要条件。
根据第3节的理论分析计算星下点轨迹调整的机动策略,若限定轨道调整时间在1 d以内,求解的2个脉冲近优解为[-85.137,152.083] m/s,分别对应将目标位置西侧的第11个上升段星下点轨迹调整到目标位置,以及将目标位置东侧的第12个上升段星下点轨迹调整到目标位置。比较发现第1个脉冲更小,可作为最优解。以最优脉冲进行星下点机动的结果如图6所示,其中实线表示飞行器原轨道星下点轨迹,虚线表示机动后星下点轨迹,点划线和星号分别表示目标再入点所处纬度和经纬度位置星下点轨迹在机动调整后经过了目标位置,而且最优解所进行的轨道改变幅度最小。由于仿真中使用的是J2模型,结果与实际轨道有微小误差,计算得到的星下点轨迹在目标纬度处经度与目标经度相差0.016 8°,精度满足任务要求。
经过星下点机动调整,得到了满足直接离轨必要条件的新轨道,经过机动后轨道形状由原来的近圆轨道变成了小偏心率椭圆轨道,在此基础上继续进行离轨制动规划仿真。

图6 星下点机动结果Fig.6 Results of ground track manipulation
离轨制动仿真中使用第2节中的2层规划方法,以脉冲模型式(9)的计算结果为初始值,计算有限推力下的最优离轨参数。规划结果如图7所示,虚线表示星下点机动后轨道星下点轨迹通过再入点经纬度位置的所在弧段,粗实线表示发动机施加制动推力的离轨段轨道星下点轨迹,细实线表示之后自由下降的过渡段轨道星下点轨迹,实心圆表示离轨点经纬度位置(224.741 5°,-32.241 2°),方形表示制动推力结束点经纬度位置,点划线和星号分别表示目标再入点所处纬度和经纬度位置。仿真得到的再入点位置符合任务要求(经纬度误差0.020 7°),具体的离轨点参数见表3。
从表3得到的仿真结果可知,通过再入点的星下点机动后,飞行器轨道满足直接离轨必要条件,就可以顺利通过有限推力的离轨规划方法计算得到最优离轨的一系列参数。
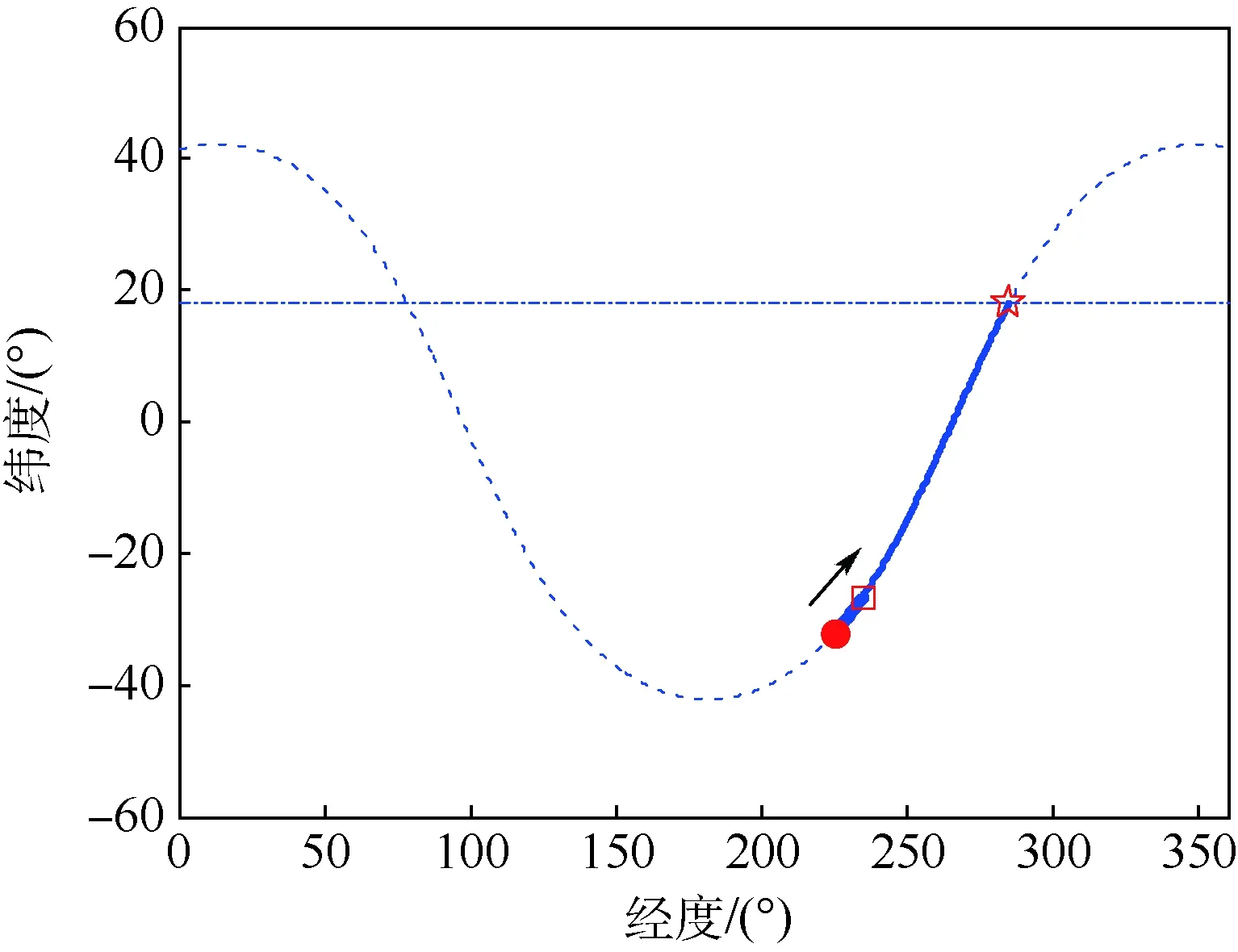
图7 离轨过程的星下点轨迹Fig.7 Ground track of deorbit process

参 数数 值离轨时间/s61676.763制动角/(°)-153.635推力时间/s164.783燃料/kg64.457
5 结 论
本文分析研究了再入飞行器限制再入点经纬度位置情况下的离轨制动任务规划方法。
1) 建立了冲量条件下计算椭圆轨道最优离轨参数的模型,并提出了限定再入点地理经纬度前提下直接离轨的必要条件。
2) 当轨道参数满足直接离轨必要条件时,完善以固定有限推力规划计算离轨点位置和离轨推力参数的方法。但对于一般任务来说,初始轨道参数往往不满足直接离轨条件,因此随后研究了一般初始轨道情况下对指定星下点目标经纬度的轨道机动方法。
3) 以具体任务参数对星下点机动调整和离轨制动理论进行了仿真验证,得到的仿真结果符合理论推导,满足任务精度要求。
