群组目标空间方向关系研究进展

禄小敏，闫浩文，王中辉

（1. 兰州交通大学 环境与市政工程学院，甘肃 兰州 730070；2. 兰州交通大学 测绘与地理信息学院，甘肃 兰州 730070；3. 甘肃省地理国情监测工程实验室，甘肃 兰州 730070）

0 引 言

空间方向关系是指在一定的方向参考系统下从参考目标到源目标的指向[1-2]。在4种空间关系（空间方向关系、空间拓扑关系、空间相似关系、空间距离关系）中，它是自然语言中运用最广的一种。不仅如此，它在空间分析、空间推理与查询及地图综合中都有很重要的运用。

群组目标是多个单目标因为形态相似、距离相近、语义相近而组成的一个视觉整体，在地理空间中，很多目标都是以群组的形式存在的，如居民地群、道路网、河流网等。在进行空间方向关系判断时，人们不仅需要判断空间单个目标之间的方向关系，很多情况下还需要判断群组目标之间的空间方向关系，如在进行工业区选址的时候，需要综合考虑工业区与附近居民地群及道路网之间的方向关系。

空间方向关系描述模型利用矩阵等形式化的方式描述抽象的方向关系，是计算和描述两目标之间空间方向关系的重要理论工具[3]。截至目前，对于单目标空间方向关系描述模型的研究已比较成熟，主要有锥形模型、投影模型和基于Voronoi图的模型等。而对于群组目标空间方向关系模型的研究零星而粗浅。

为此，本论文对现有的群组目标空间方向描述模型进行了归纳总结，描述了它们的优缺点，并提出了进一步研究的设想。

1 群组目标概述

1.1 群组目标概念

群组目标是多个单目标由于空间关联度高而形成的集合。在地理空间中，许多目标都是以群组的形式出现的，群组目标按照其构成的单目标属性可以分为空间点群、线群、面群及混合群。常见的点群有控制点群等；常见的线群有道路网、河流网等；常见的面群有居民地群、湖泊群；混合群则是前面三类群组目标的混合，常见的有村庄、街区等，如图1所示。

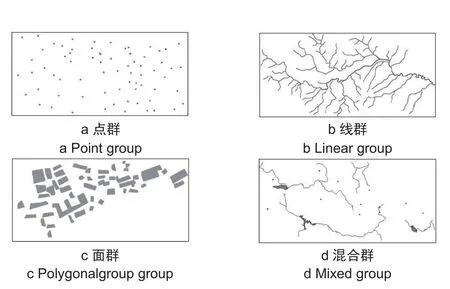
图1 群组目标Fig.1 Object groups

1.2 群组目标空间方向关系的特点

相对于单个目标，群组目标空间方向关系有其特殊之处，主要表现在以下几个方面[4]：

1）复杂性

相对于空间单目标，群组目标的空间方向关系判断是一个复杂的空间计算过程。特别是在群组目标之间相互缠绕、交叠、包罗时，其描述与计算将变得异常复杂。

2）多方向性

由于群组目标自身覆盖面较广，会导致利用单一的方向描述过于片面，如图2所示的情形下，群组目标B相对于群组目标A的方向关系应表示为Dir（A,B）={N,NE,E,SE}。

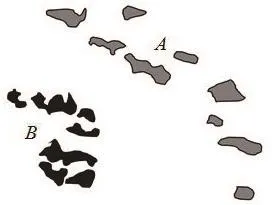
图2 群组目标方向关系的多方向性Fig.2 The multi-directionality of spatial direction relations between object groups

3）整体性

群组目标即是一个视觉整体，在进行空间方向关系判断的时候，也通常将其视为一个“整体”对“整体”的相互关系。

1.3 群组目标空间方向关系影响因素

Goyal[5]和Peuqeut[6]等人指出空间目标的距离、形状以及分布范围等都会对方向关系产生影响；王中辉[4]指出群组目标的分布范围和分布密度也会影响群组目标之间的方向关系。归纳起来，群组目标空间方向关系受以下因素影响：

1）群组目标之间的空间距离

根据人体视觉成像原理，近处的目标显得大而远处的目标显得小，所以同样的源目标相对于参考目标，其大小会随着距离的增大而缩小，对应的空间方向关系也会受到影响，如图3所示，居民地群B与C具有相同的空间形态、分布范围，但由于它们距湖泊群A的距离不同，导致其方向关系明显不同，Dir（A,B）={NE,E}而Dir（A,C）={NE}。

图3 距离对群组目标空间方向关系的影响Fig.3 The effect of distance on spatial direction relations of object groups

2）群组目标的分布范围

群组目标的分布范围大小会影响群组目标之间的方向关系。同样水平距离情况下，对应的空间方向关系会由于群组目标分布范围的不同而不同。如图4所示，居民地群B和C分布形状相同，距离点群污染源A的距离相同，但由于其分布范围不同，导致其与点群A的方向关系不同，Dir（A,B）={NE,E,SE}而Dir（A,C）={E}。

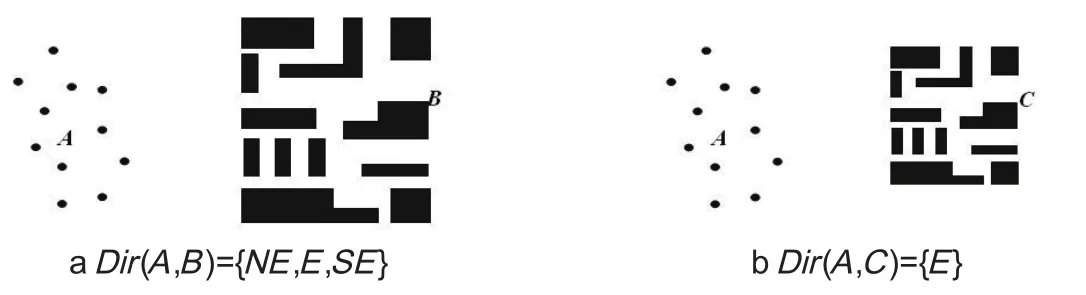
图4 分布范围对群组目标方向关系的影响Fig.4 The effect of distribution scope on spatial direction relations of object groups

3）群组目标的空间形状

群组目标的分布形状也会对方向关系判断产生影响。如图5所示，湖泊群B的分布形状发生了变化，使得湖泊群B相对于工业区A的方向关系由Dir（A,B）={N,NE,E，Same}变为Dir（A,C）={NW,N,NE}。

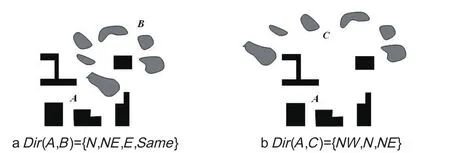
图5 分布形状对群组目标方向关系的影响Fig.5 The effect of distribution shape on spatial direction relations of object groups

4）群组目标的分布密度

群组目标之间的空间方向关系会在一定程度上受其分布密度的影响。如图6所示，工业区B相对于河系A的方向关系是Dir（A,B）={NE,E,SE}；当工业区的分布密度明显减小到C所示大小时，方向关系也随即发生了变化，Dir（A, C）={NE,SE}。

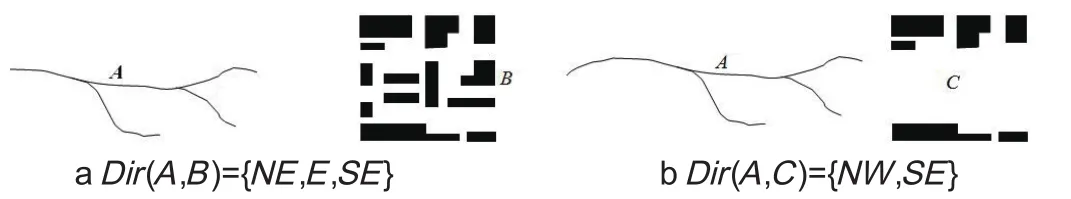
图6 分布密度对群组目标方向关系的影响Fig.6 The effect of distribution density on spatial direction relations of object groups

2 群组目标空间方向关系模型

目前，有关群组目标空间方向关系模型的研究比较少，已有的模型有基于凸壳的模型[7]、基于“剥皮”法和方向关系矩阵的模型[8]、基于方向Voronoi图的模型[9]以及利用地学信息图谱的模型[10]。下面就其原理及其优缺点做一论述说明。

2.1 基于凸壳的群组目标方向关系模型

该模型的基本思路是通过计算源目标群的凸壳，将源目标群转化为空间单目标，在此基础上利用空间单目标方向关系判断模型来计算群组目标空间方向关系。具体如图7所示。

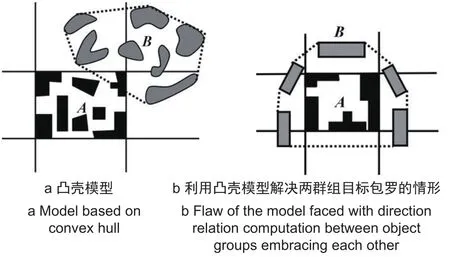
图7 凸壳模型及其缺陷Fig.7 The convex hull model and its defects

该模型的优点是算法简单，但其缺点也显而易见，首先，利用凸壳来代替源目标群，具有很大的近似性，没有很好地考虑群组目标的空间形态，如对于图7a所示的情形，源目标群位于参考目标群的北、东北及东方向，但运用本模型所得的方向关系却是Dir（A,B）={N,NE,E,Same}；不仅如此，当两目标出现包罗等情况时，利用该模型判断方向关系有可能会得出错误结论，如图7b所示，源目标群位于参考目标群西、西北、北、东北、东、东南、西南方向，但运用本模型所得的方向关系却是Dir（A,B）={N,NE,E,SE,S,SW,W，NW,Same}。其次，方向关系矩阵自身就有一定的缺陷，如用参考目标群的最小投影矩形（MBR，Minimum Bounding Rectangle）代替参考目标群做方向关系分析，具有很大的不精确性。

2.2 基于“剥皮”法和方向关系矩阵的模型

该模型的基本思路是：将源目标群进行带约束的Delaunay三角剖分；之后利用动态阈值“剥皮”法，求得源目标群的分布边界多边形；最后将其引入到方向关系矩阵模型求得方向关系矩阵，具体如图8所示。

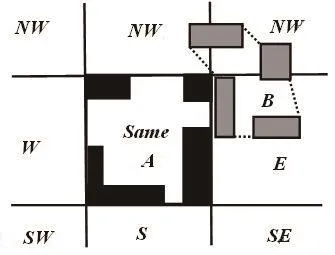
图8 基于“剥皮”法的模型Fig.8 The model based on "stripping"

该模型在基于凸壳方法的基础上引入了动态阈值“剥皮”法，利用源目标群的分布边界多边形代替了2.1方法中的凸壳，精度有了一定提高，并且可以避免缠绕、交叠、保罗等特殊情况对方向关系判断的影响。但此模型仍然不可避免地继承了方向关系矩阵模型的缺点。

2.3 基于方向Voronoi图的群组目标空间方向关系模型

该模型是在针对空间单目标方向关系计算的Voronoi图模型基础上发展而来的，该模型首先对构成参考目标群和源目标群的单个子目标进行带约束的Delaunay三角剖分[11-12]；进而在参考目标群与源目标群之间构建可视区域并生成方向Voronoi图；最后计算Voronoi图中各构成边的方位角并将其归类，求得每一类方位角上Voronoi边的百分比，进而得到参考目标群相对于源目标群的方向关系，具体如图9所示。

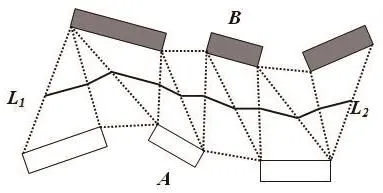
图9 群组目标间的方向Voronoi图Fig.9 Voronoi diagram of direction relations between object groups

该模型可以较好地计算群组目标之间的空间方向关系，得到的定量结果比较精确。但整个过程中，需要对子目标进行三角剖分、构建可视链、生成Voronoi图、求解每一条Voronoi边的方位角，计算过程比较复杂，而且无法为进一步的空间查询与空间推理提供良好的支持。

2.4 群组目标空间方向关系的图谱描述模型

该模型引入了数学形态学以及地学信息图谱概念[13-14]，将参考目标群的MBR每隔一定角度向外无限膨胀[15]；求得每次形态变换后参考目标群与源目标群的交集；最后，在此基础上求得谱密度，提取图谱特征并绘制方向关系图谱的谱向量分布图，具体如图10所示。

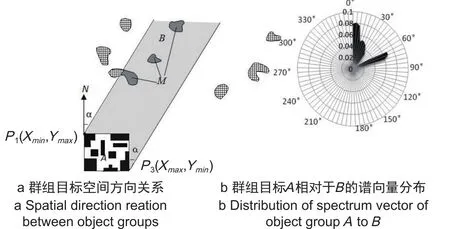
图10 群组目标空间方向关系图谱描述模型Fig.10 The graph-spectrum expression model of of spatial direction relations between object groups

如图10b所示，该模型可以用可视化的形式直观表达群组目标空间方向关系；还可以用表1所示的方向分布角度范围以及谱密度均值、方差等对群组目标空间方向关系进行比较精确的定量描述；不仅如此，该模型还能够将空间形态、分布范围、分布密度以及相互之间的距离关系等对空间方向关系的影响反映出来。但是，该模型仍然利用参考目标群的MBR代替MBR，导致在向外膨胀与源目标群求交集过程中产生误差。

表1 群组目标A与B的方向关系图谱特征Tab.1 The graph-spectrum characters of spatial direction relations between object groups A and B

综上所述，群组目标空间方向关系是空间关系中一个重要分支，但是关于它的研究比较少，已有研究也都有不同缺陷，其相关研究还亟待去钻研并推进。

3 结束语

本文对群组目标及其方向关系相关概念及影响因素进行了阐述，并对已有研究及其模型进行了归纳评价。总的来看，群组目标空间方向关系相关研究还比较欠缺，其研究内容和研究范围仍需进一步扩大。一方面，GIS本身的理论、技术和需求促使群组目标空间方向关系须向多维、多层次方向发展；另一方面，群组目标空间方向关系也要与其他诸如计算机智能等领域结合，以便更好地服务于空间认知、空间查询、空间推理与地图综合。