基于货物运到期限的编组站动态配流优化研究

李晟东，徐长安，吕红霞*,c，李文新

(西南交通大学a.交通运输与物流学院；b.全国铁路列车运行图编制研发培训中心；c.综合交通运输智能化国家地方联合工程实验室，成都610031)

0 引 言

货物运到期限是指铁路运输部门规定的货物运输一定里程所需要的时间标准.保障运到期限，是履行对托运人关于货物运输时间的承诺，对加快货物送达，保证运输质量，提高铁路货物运输市场竞争力有重要意义.

货物运输时间由技术站中转时间、区间运行时间和装卸作业时间组成.货物的区间运行和装卸站作业环节简单，作业时间容易控制，而技术站的作业环节多且复杂，导致技术站中转时间难以控制.因此应主要从技术站，尤其是编组站作业入手以保障运到期限.

编组站阶段计划作为车站作业计划的具体安排，主要包括：配流计划、调机运用计划和到发线运用计划，其中配流计划与调机运用计划联系紧密，而到发线运用计划相对独立.配流计划确定出发列车的车流来源，是阶段计划的主要内容，直接影响货物在编组站的中转时间.因此在配流环节对运到期限加以考虑，将极大地保障铁路货物运到期限.

王慈光[1]将配流问题分为静态配流和动态配流，静态配流是在解编方案确定的前提下研究合理配流，动态配流的前提条件则是解编方案不确定.关于静态配流的研究中，薛锋等[2]建立了双向编组站静态配流的双层多目标决策模型，利用禁忌搜索策略和配流网络相结合的算法求解；景云等[3]通过构建网络模型，将静态配流问题转化为固定费用的产销平衡运输问题.关于动态配流的研究中，何世伟等[4]建立了阶段计划解编作业与车流推算优化混合0-1规划模型，并给出了启发式分解算法；王明慧等[5]综合优化编组站列车解体、配流、编组及到发线运用计划，并设计了启发式算法求解；王正彬等[6]结合求解运输问题的表上作业法，设计了混合遗传算法.国外研究中，S.Yagar等[7]提出了一种HSS算法，并采用动态规划的方法，寻求最优的解编顺序；Mark A.Turnquist等[8]运用排队论模型求解编组站列车解编顺序.

既有研究中较少考虑运到期限，文献[9-10]考虑了运到期限因素，但都是先构造列车解编顺序，将问题转化为静态配流问题进行研究.本文在编组站配流中考虑运到期限，综合考虑调机运用计划与配流计划，建立0-1规划模型，并设计模拟退火算法求解.

1 数学优化模型

1.1 建模分析

编组站配流优化模型中，对于运到期限的考虑主要体现在如下目标函数与约束条件方面.

(1)目标函数.

不同货物对运输时效性的要求不同，以车流在站停留时间加权值的总和最小为优化目标构建目标函数，此权重体现对于时效性要求高的货物在配流中的优先考虑.

而运输时效性要求高与低是一个模糊概念，因此本文以运到期限等级的概念表示货物对运输时效性的要求，即目标函数中的权重，同时以模糊数学相关理论定量化确定运到期限等级评判方法.划分运到期限等级评语集V={V1,V2,V3,V4,V5}={低，较低，一般，较高，高}，对应模糊等级为D={1,2,3,4,5}，进而构建梯形隶属函数为

(2)约束条件.

在约束条件方面，将运到期限分配至编组站配流环节，通过保证配流环节的时限要求，以保障运到期限.货物运输作业环节主要包括货物作业停留、技术站中转作业及区间运行等.由文献[9]可知，货物作业停留时间、技术站中转作业时间(分有调和无调中转作业时间)及区间运行时间等都可由正态分布描述，因此有，ui为Xi的均值，为X的方差，i=1,2,…,n，X为作业环节i消耗的ii时间.则由正态分布相关性质可知，货物运输全程时间Y也服从正态分布，其分布形式为

因此在分配运到期限到货物运输各个环节时，可采用均值比例分配法，指按货物运输各个环节的平均作业时间占总时间的比例分配运到期限，即

式中：Ti为作业环节i的时限要求；T为货物运到期限；ti为作业环节i的平均作业时间，可由《全国铁路统计资料汇编》等资料获取.

因而对于一批货物，通过车流径路和编组计划等文件，可得知其从始发站至终到站的运行路径，途经的技术站，技术站中转作业类型等信息，即得知货物运输全程包含的作业环节，进而利用均值比例分配法分配运到期限，得到货物在各环节的最大时限.当运到期限分配至作业环节i后，可进一步计算得到该环节的保障率pi为

1.2 模型假设

本文所建模型条件假设如下：

(1)1台调机解体、1台调机编组的作业系统；

(2)本站作业车、转场车从驼峰进入系统；

(3)不考虑部分改编中转列车；

(4)有足够的到达线、调车线、出发线等线路.

1.3 符号说明

参数：[Tjhs,Tjhe]为计划的编制时段；D为到达列车集合，D={d1,d2,…,dn}，i为到达列车索引，d1为虚拟到达列车，表示计划编制起始时调车场的现车，Ki为到达列车i包含的货车数，k为到达列车i的货车索引；F为出发列车集合，F={f1,f2,…,fm}，j为出发列车索引，fm为虚拟出发列车，表示计划编制结束时调车场的残存车；Td为到达列车到达时刻集合，Tdi表示到达列车i的到达时刻；Tf为出发列车出发时刻集合，Tfj表示出发列车j的出发时刻；Tjd、Tjj、Tjb和Tjf分别为到达、解体、编组和出发技术作业时间；gikj表示到达列车i中的货车k按编组去向是否能编入出发列车j，是为1，否为0；wik、lik分别表示到达列车i中货车k的重量和换算长度；和分别表示出发列车j的最小重量、最大重量、最小换算长度和最大换算长度的编组要求；αik为到达列车i中货车k的货物运到期限等级；Tik为到达列车i中货车k的在站最大停留时间.

变量：tikj为到达列车i中货车k编入出发列车j的在站停留时间；为到达列车i的解体开始时刻；为出发列车j的编组结束时刻；φikj表示若到达列车i的解体结束时刻早于出发列车j的编组开始时刻，则到达列车i中货车k可编入出发列车j，此时φikj取值为1，否则为0为0-1变量；表示到达列车i是否按最早解体开始时刻Tzjs(Tzjs=Tdi+Tjd)解体，是为0，否为1；表示出发列车j是否按最晚编组结束时刻Tzbf(Tzbf=Tfj-Tjf)编组，是为0，否为1；xikj为0-1决策变量，表示到达列车i中货车k是否编入出发列车j，是为1，否为0.

1.4 优化模型

基于货物运到期限的单解单编系统的编组站动态配流优化模型为

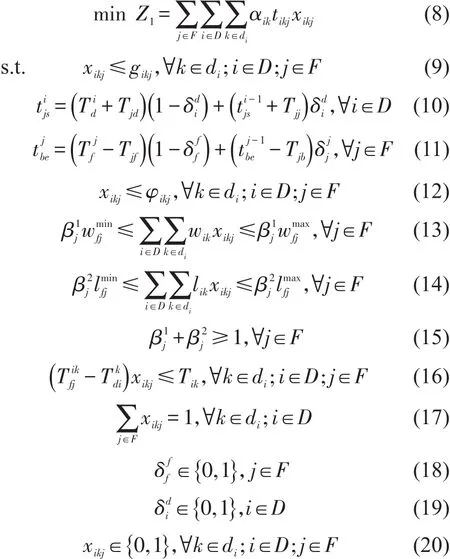
式(8)为车流在编组站停留时间加权值最小化的目标函数；式(9)为车流的编组去向约束；式(10)和式(11)分别为到达列车和出发列车的解体开始时刻和编组结束时刻约束，控制列车尽早解体和尽晚编组，使车流有编入更多出发列车的可能，其中虚拟到达列车解体结束时刻等于Tjhs，虚拟出发列车编组结束时刻等于Tjhe；式(12)表示车流只能编入编组开始时刻晚于其解体结束时刻的出发列车；式(13)和式(14)分别为出发列车的编组重量和换长约束，式(15)表示出发列车只需满足重量或换长1个编组要求即可；式(16)为车流的在站最大停留时间约束；式(17)为车流的唯一指派约束；式(18)～式(20)为变量的0-1约束.

2 算法设计

n个到达列车，m个出发列车，每个到达列车包含k个货车的配流方案数为(mk)n，难以用精确算法求得最优解.模拟退火(Simulated Annealing，SA)算法是求解大规模组合问题的有效算法，能够在理想的时间内求得满意解，因此设计SA算法求解模型.

模型所求目标包括列车解编顺序和出发列车车流来源，可视为双层结构，同时，不合理的列车解编顺序下，不一定产生可行的配流方案.因此模型求解思路为：上层结构通过一定的准则得到合理的列车解编顺序，并作为已知条件输入下层结构以求解出发列车车流来源，此时模型的解编顺序已定，可调用CPLEX求解出发列车车流来源，即得到1个配流方案，通过SA算法循环迭代，得到模型优化解.

模型中，列车解编顺序对配流的影响体现在式(9)、式(12)和式(16)，用max(Ki)×m×n的三维0-1矩阵M1、M2和M3分别表示约束式(9)、式(12)和式(16)的约束矩阵，其中式(16)可转化为式(9)和式(12)的形式.定义约束矩阵M以确定上层结构合理的列车解编顺序，约束矩阵M的产生规则为：当M1、M2和M3的同一位置值都为1时，M的该位置取值为1，否则为0.则约束矩阵M某一列的和mj表示对应出发列车j最大可配入货车数量，为每一mj设定阈值[aj,bj]，当所有mj满足阈值要求，即M满足阈值要求时，则得到合理解编顺序.

算法具体步骤如下，算法流程如图1所示.

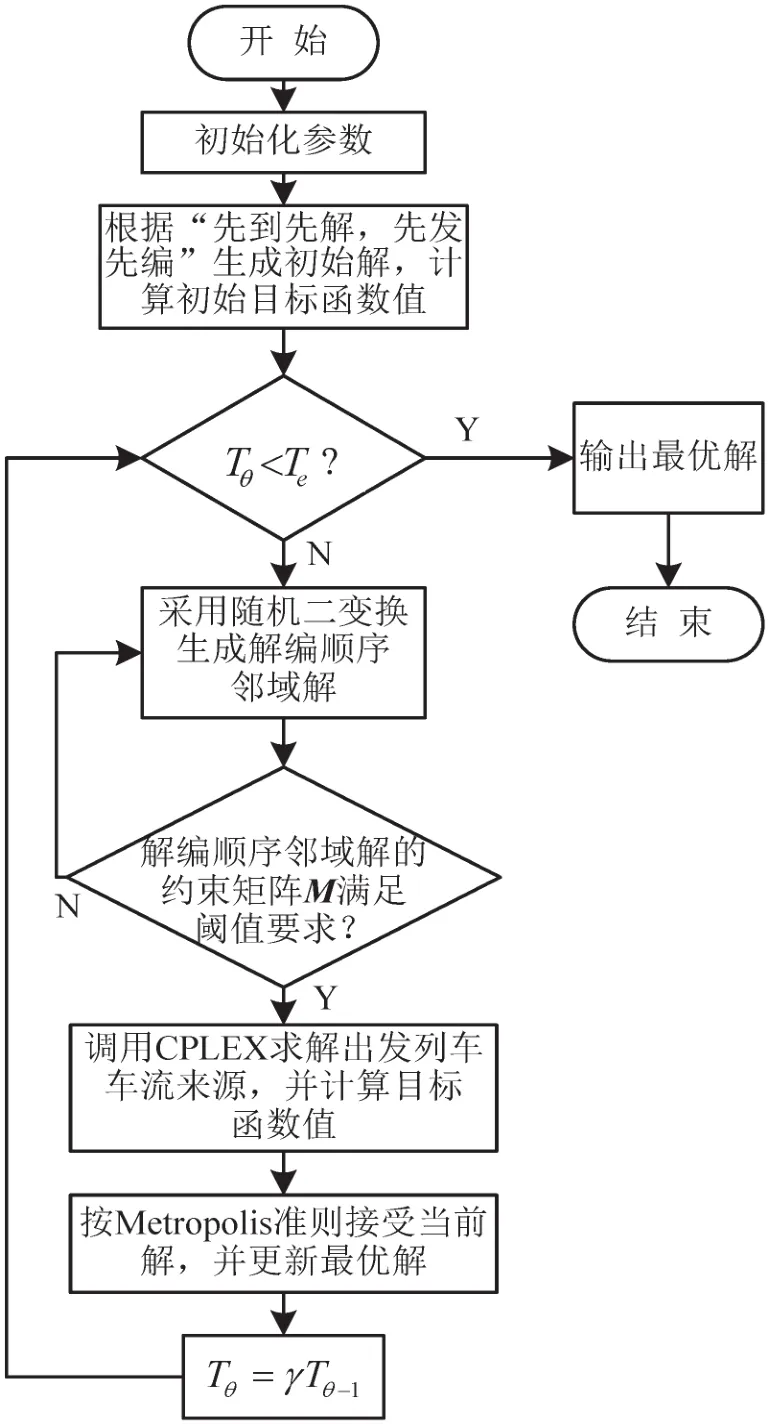
图1 模拟退火算法流程图Fig.1 Simulated annealing algorithm flow diagram

Step1 初始化算法参数，包括初始温度Ts，终止温度Te，温度衰减系数γ，马尔科夫链长度δ，当前成功迭代次数θ等.

Step2 根据“先到先解，先发先编”的规则设定初始列车解编方案，并调用CPLEX求解出发列车车流来源，以此计算得到初始目标函数值Z0，记录当前最优目标函数值B=Z0.

Step3 采用随机二变换的方法生成解编顺序邻域解，随机选定当前解体顺序中的2列列车，交换其解体顺序位，采用同样的方法生成新的编组顺序.

Step4 计算解编顺序邻域解的约束矩阵M，若M满足阈值要求，转Step5；否则，转Step3.

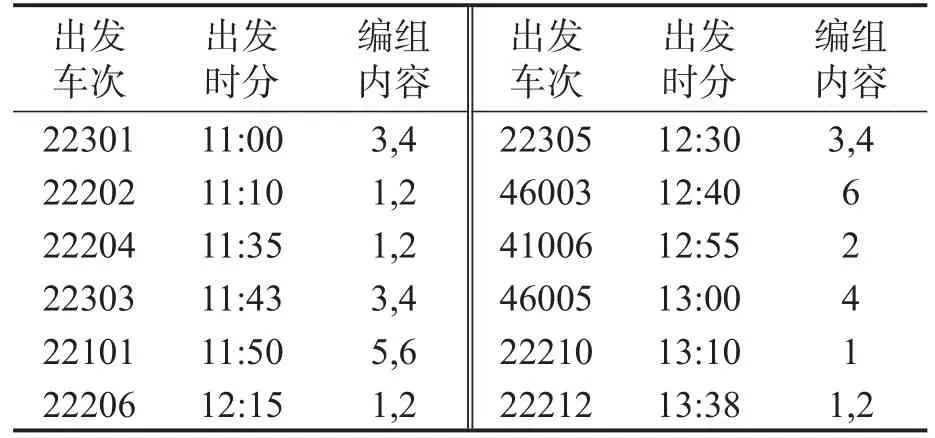
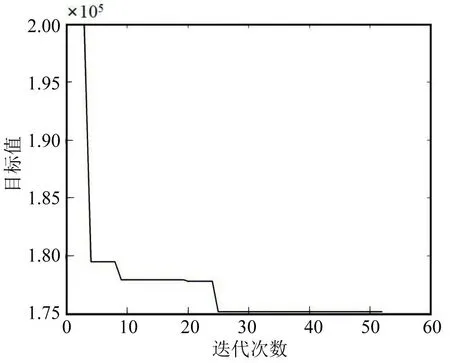
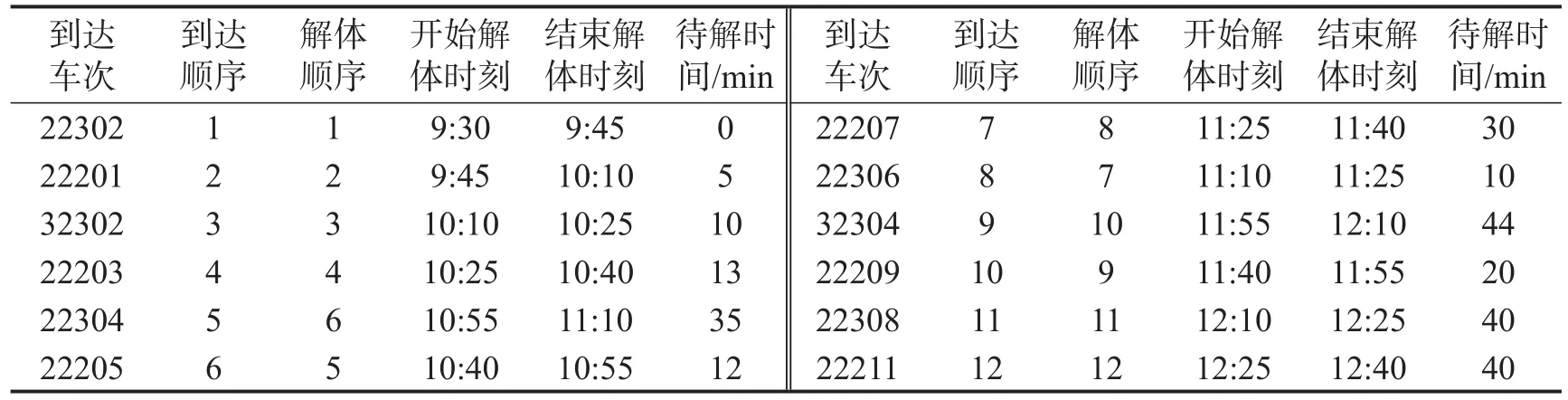
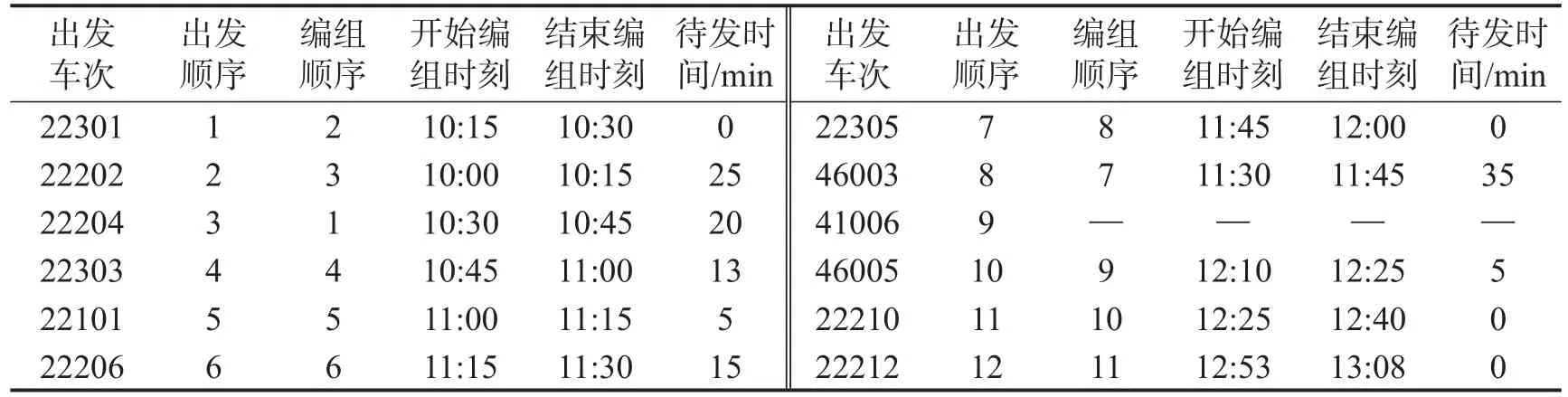
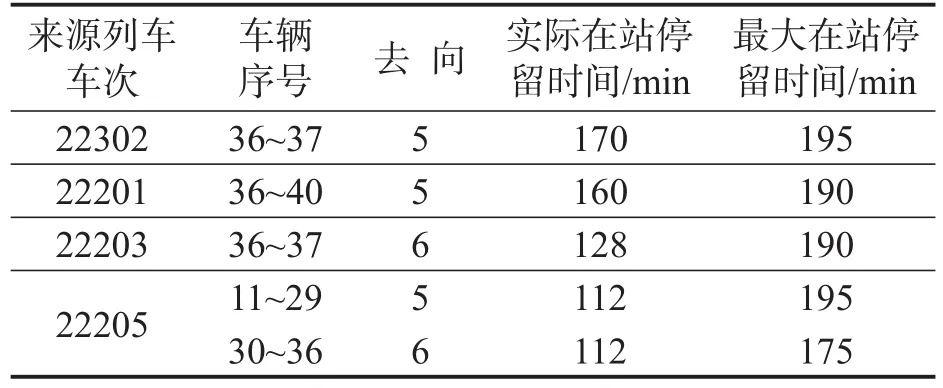
Step5 求解解编顺序邻域解下的出发列车车流来源，以此计算得到目标函数值Zθ.若Zθ

Step6Tθ=γTθ-1，若Tθ

3 算例分析

某二级三场编组站解体、编组调机均为1台，列车到达作业时间为30 min，出发作业时间为30 min，解体作业时间为15 min，编组作业时间为15 min.到达车流信息如表1所，出发车流信息如表2所示，车流运到期限信息(由于篇幅原因，仅列举22302次列车信息)如表3所示.

表1 到达列车车流数据Table 1 Wagon-flow data of arriving trains

表2 出发列车车流数据Table 2 Wagon-flow data of departing trains

在CPU为Inter Core i7-6700HQ，RAM为16G的个人计算机上，采用Matlab2016a编程，经过多组参数实验，在初始温度为99，终止温度为1，温度衰减系数为0.9下，求解得到目标函数值为175 174，算法收敛曲线如图2所示，列车解编和配流方案如表4～表6所示.

图2 算法收敛曲线图Fig.2 Algorithm convergent curve diagram

表4 优化列车解体方案Table 4 Optimized train disintegration scheme

表5 优化列车编组方案Table 5 Optimized train marshalling scheme

表6 优化配流方案Table 6 Optimized wagon-flow allocation scheme

可知，到达列车的解体顺序为{1,2,3,4,6,5,8,7,10,9,11,12}，出发列车的编组顺序为{2,3,1,4,5,6,8,7,-,9,10,11}，其中41006次列车因为车流接续不足而停运，同时所有车流实际在站停留时间均未超过最大在站停留时间，如表7所示，从而验证了本文模型及算法的有效性.

表7 22101次列车车流在站停留时间Table 7 Residence time of 22101 train’s wagon-flow

4 结论

将货物运到期限分配至编组站配流环节，保证车流在编组站的最大停留时限，能够实现在货物运输主要环节上保障运到期限.本文基于单解单编的编组站作业系统，构建了调机运用与配流综合优化的0-1整数规划模型，设计了模拟退火算法求解模型，算例分析结果表明，本文基于运到期限构建的动态配流模型及算法具有良好的有效性.本文考虑了货物运输的编组站作业环节，考虑货物运输整个环节以保障运到期限是本文的下一步研究方向.