道路交通噪声预测声源简化研究

李宪同，赵佳美，汪 贇，白 煜，宗蕙娟，温香彩

1.中国环境监测总站，国家环境保护环境监测质量控制重点实验室，北京 100012 2.北京市劳动保护科学研究所，北京 100054

国内学者也进行了相关研究，包括道路交通噪声预测模型的推导[10]、参数修正[11-13]、衰减修正[14]等。环境影响评价工作中，技术人员通常依据《环评导则》将道路简化为1条位于道路中心线处的线声源，而不考虑道路宽度和车道多少。《环评导则》中规定的简化为1条线声源与其他模型中简化为多条线声源在道路宽度不同、接收点与道路边界距离不同时对预测结果的精度有无影响、影响有多大，很少有文章涉及。本文通过推导多条线声源与1条线声源在接收点噪声影响的误差计算公式，深入研究《环评导则》中的简化方式的误差大小，以期为道路噪声管理、规划、环评提供更加切实可行的方法，减少道路交通噪声投诉和影响。

1 误差计算

一般情况下，是将近场区的道路交通有限长线声源当作无限长线声源处理[15]。如图1所示，假设接收点在距离线声源距离r0处(参考点)声级为Lr0，在距离r处声级为Lr，衰减符合式(1)的规律。

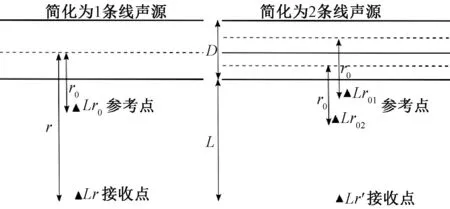
图1 两车道道路线声源简化示意图Fig.1 Diagram of simplified sound source for two-lane road

(1)

道路声源简化为线声源的条数越多，与道路声源的真实辐射情况越接近，预测结果越接近道路真实排放情况[6]，按照上述理论计算两车道道路交通噪声简化为2条线声源和简化为1条线声源时接收点处噪声值的误差。

假设两车道道路宽度为D，接收点与道路边缘距离为L。简化为1条线声源时，线声源位于道路中心线处，则接收点到线声源的距离r可由L和D表示：

r=L+D/2

(2)

两车道的道路简化为2条线声源时，假设车速相同，2条线声源声能量相同。则每条线声源在距离r0处的声级L01与L02相等，两者声能量之和等于Lr0。则

L01=L02=Lr0-10lg2

(3)

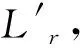
(4)

简化为2条线声源与简化为1条线声源在接收点处噪声值预测结果的误差ΔL如式(5)所示。

(5)

令n=L/D，则

和祖父的想法一样，我也不想成为什么“家”，因为作家与艺术家，既与才华和努力有关，也与时运有关，与命途有关，真正的成功者只是极少数。我们只要将爱好融入生命里，在其中得到乐趣，就是真正的价值所在。如果每一位写作者或画者都用真诚的心去写，去画，相信这个世界就会因为书写、绘画，而变得更加美好。我觉得，自己即使张罗着大小琐碎事，也能享有趣味充实的生活，就已经是成功的人生，不必太在意世俗的眼光，把别人的框架，硬套在自己的身上。

(6)

可以得到ΔL与n之间的变化关系如图2所示。

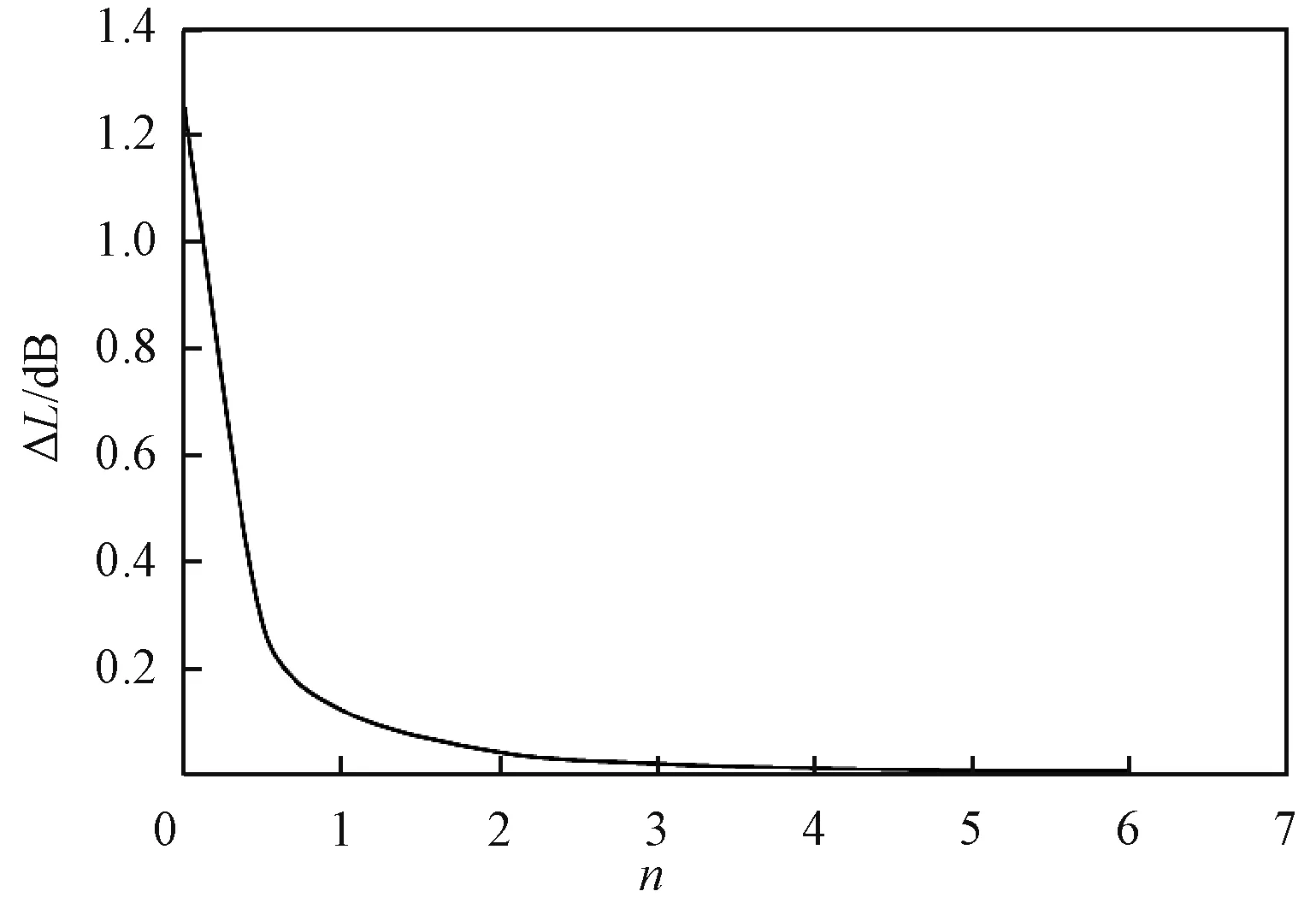
图2 两车道1条线声源与两车道2条线声源误差变化Fig.2 The error variation of one linear sound source and tow linear sound sources

从图2可以看出，误差只与L和D有关。简化为2条线声源比简化为1条线声源的声级预测结果大。n越小，绝对误差越大，随着n增大，绝对误差呈对数减小。

依此类推，可以得出四车道、六车道、八车道和十车道道路简化为1条线声源与多条线声源的误差公式。

对于四车道道路，不同简化方式的绝对误差：

(7)

对于六车道道路，不同简化方式的绝对误差：

(8)

对于八车道道路，不同简化方式的绝对误差：

(9)

对于十车道道路，不同简化方式的绝对误差：

(10)

不同道路宽度时，根据公式计算得到的1条线声源与多条线声源之间的误差ΔL的变化趋势如图3所示。

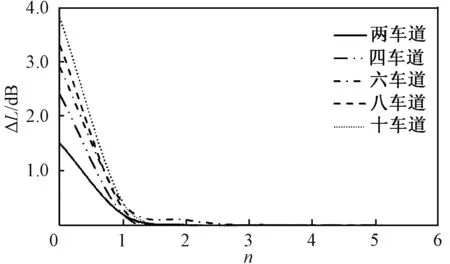
图3 不同道路宽度1条线声源与多条线声源误差变化Fig.3 The error variation of one linear sound source and multiple linear sound sources with different roads width

从图3可以看出，对于不同道路宽度，n与绝对误差的关系与两车道时规律一致。并且道路宽度越大，将道路交通声源简化为1条线声源和多条线声源预测结果的绝对误差越大。当接收点位于道路边缘(n=0)时，绝对误差最大，均超过1 dB，且对于十车道的道路，误差大于3 dB。当接收点与道路边缘的距离大于道路宽度的一半时(n大于0.5)，绝对误差可以控制在0.5 dB之内。

2 验证分析

2.1 基于Predictor-lima 预测软件验证

Predictor-lima环境噪声计算和绘图软件是由丹麦B&K公司研发的，是国际上主流的预测软件之一。《环评导则》中的公路交通运输噪声预测模式由车流量计算一个噪声基本值，再对车型比例、速度、衰减距离、路面情况和其他环境等因素加以修正。

本文分别对两车道、四车道、六车道、八车道、十车道的道路交通噪声进行预测，6个接收点(N0、N1、N2、N3、N4、N5)与道路边缘的距离分别为路宽的0、1、2、3、4、5倍(即n=0、1、2、3、4、5)，以两车道和四车道为例，预测模型示意图分别见图4、图5。

图4 两车道简化为1条线声源和2条声源模拟图Fig.4 Simulated diagram of two-lane road simplified to one linear sound source and two linear sound sources

图5 四车道简化为1条线声源和4条线声源模拟图Fig.5 Simulated diagram of four-lane roa simplified to one line sound source and four linear sound sources

预测计算结果如图6所示。从图6可以看出，经国际上主流的预测软件预测得到的n与绝对误差的变化规律与理论分析的结果基本一致，一定程度上验证了前述的理论分析。

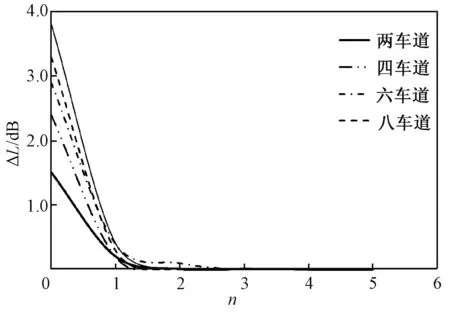
图6 不同道路宽度时1条线声源与多条线声源之间的误差变化预测结果Fig.6 The prediction results of the error variation ofone linear sound source and multiple linearsound source with different roads width

2.2 实测验证

选取北京市北苑东路(清河郊野公园西门北侧路段)，该道路为双向四车道，最外侧有1条辅路(无车辆通过)，中间有一条宽度约6 m的绿化带，道路总宽度约20 m。分别在与主路边缘的距离为0、1、2、3倍道路宽度处布设了4个测点，测试过程中无大、中型车经过，各车道平均车速约为55 km/h，远侧2个车道的车流量为900辆/h，近侧2个车道的车流量约为1 500辆/h。实际车流量并非如理论计算中平均分布，故按照实际情况输入简化为1条线声源和简化为4条线声源的预测参数，结果如表1所示。

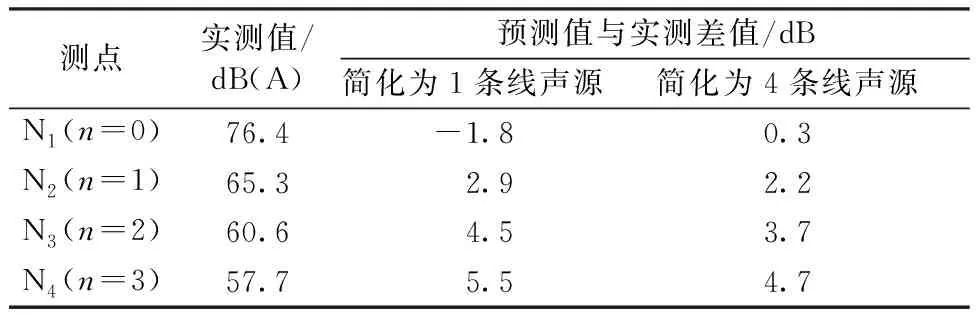
表1 不同测点预测值与实测差值Table 1 The difference between the predictedvalue and the measured value

从表1可以看出，尽管实测道路交通噪声结果与预测结果并不完全一致，但简化为4条线声源的预测结果与实测值更接近，并且简化为4条线声源与简化为1条线声源引起的绝对误差与n值的变化规律与理论分析结果基本趋势一致。这验证了前面公式推论和预测验证的规律的正确性，说明简化为与车道数相同数量的线声源比简化为1条线声源的预测结果更准确。

3 声源优化分析

在实际工作中，对于八车道、十车道等车道数较多的道路，简化为与车道数相同数量的线声源的建模工作量很大，而简化为2条线声源工作量相对减少。故在前述误差计算公式的基础上，进一步推导大于或等于四车道的道路简化为2条线声源时的预测结果与简化为与车道数相同的多条线声源时对预测结果的影响大小，两者差别见表2。从表2可以看出，当车道数大于或等于6时，简化为2条线声源与简化为与车道数相同的多条线声源时的预测结果相差在0.5 dB以内，说明当车道数大于或等于6时，简化为2条线声源即可保证预测精度。当车道数小于6时，应该按照车道数简化为多条线声源。

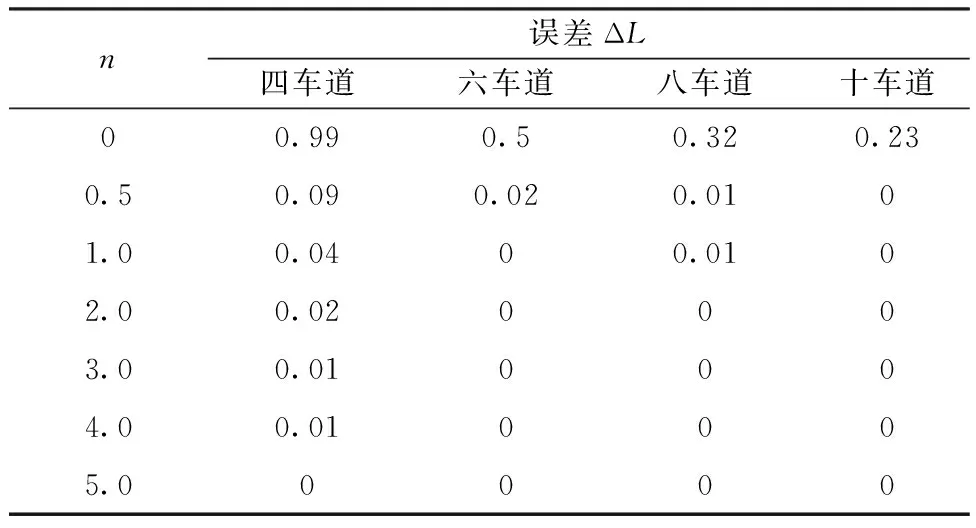
表2 不同道路宽度简化为2条线声源与简化多条线声源的预测结果差值Table 2 The error variation of 2 linear soundsources and multiple linear sound sourceswith different roads width

4 结论

1)道路交通噪声预测时，将道路声源简化为多条线声源与《环评导则》中简化为1条线声源对接收点处预测结果的绝对误差随接收点到道路边缘的距离增加而呈对数减少的规律。道路越宽，2种方法的绝对误差越大。

2)接收点到道路边缘的距离大于道路宽度时，简化为多条线声源与按照《环评导则》简化为1条线声源之间的绝对误差在0.5 dB以内；接收点到道路边缘的距离小于道路宽度时，绝对误差较大，在1～3 dB之间。

3)在按照《环评导则》开展道路交通噪声预测或其他相关研究时，对于接收点到道路边缘的距离大于道路宽度的情况，为减少计算量，建议简化为1条线声源；对于接收点到道路边缘的距离小于道路宽度的情况，为保证预测结果更接近实际情况，当车道数小于6时，建议按照车道数简化为多条线声源；当车道数大于或等于6时，建议简化为2条线声源。在实际工作过程中，这将大大减少工作量。