宽频带级联数字下变频实现方法

欧春湘，杨嘉伟

(1.北京遥感设备研究所，北京 100854;2.中国航天科工集团有限公司 第二研究院，北京 100854)

0 引言

常规的数字下变频方法很难实现瞬时宽带信号的数字下变频，宽带数字下变频的难点是滤波器的运算量太大。目前能有效减小滤波器运算量的方法主要有对称法、分布式算法和多相滤波等算法等[1]。对称法是指根据线性相位FIR滤波器系数的对称特性，进行乘累加运算之前先将对称项相加。随着FPGA中查找表结构(look up table, LUT)的出现，分布式算法得到了广泛应用，该方法利用查找表将固定系数的乘累加运算转化为查表操作[1]。用多相滤波结构的数字下变频技术是指将滤波器转化成多相结构，根据抽取的对等关系将抽取提前至滤波之前，再引入信道划分，然后根据混频序列的周期性及多相滤波结构的特点，将混频移到抽取和滤波之后进行[2-4]。本文在跳频通信系统中利用信道化技术实现宽频带数字下变频，通过对信道进行合理划分，将多相滤波中快速傅里叶变换(fast Fourier transform，FFT)运算转变成高效的离散傅里叶变换(discrete Fourier transform，DFT)运算，该结构在完成高采样率下采样率变换和宽带高效数字下变频的同时，还具备并行处理多信号的能力，单级乘法结构不仅缩短了处理时间，还减少了硬件资源[5-7]。

1 基于多相滤波的高效信道化结构

1.1 低通信号的整数倍抽取

整数倍抽取是指把原始采样序列x(n)每D个数据抽取一个，形成一个新序列xD(m)，即

xD(m)=x(mD)，

(1)

式中：D为整数。

假设x(n)的频谱为X(ejω)，则xD(m)的频谱XD(ejω)为抽取前原始频谱x(n)经D倍展宽和频移后D个频谱的叠加和。

(2)

如果低通x(n)的取样率为fs，则xD(m)的取样率为fs/D，xD(m)的无模糊带宽为fs/2D，xD(m)可以准确地表示x(n)中小于π/D或fs/2D的频率分量信号，所以对xD(m)进行处理等同于对x(n)的处理。然而xD(m)的速率只有x(n)的1/D，大大降低了后续处理速度的要求。一个完整的D倍抽取器结构如图1所示[8-10]。

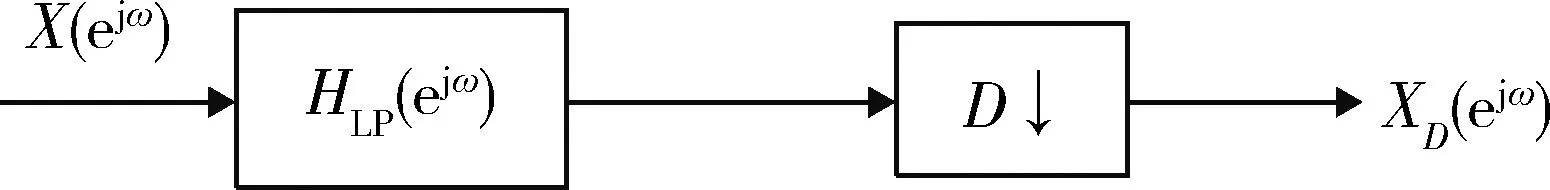
图1 完整抽取器方框图
Fig.1 Illustration of completed decimator

1.2 高效信道化结构

信道化接收原始结构如图2所示，图中hLP(n)为原型低通滤波器，其频率特性如式(3)，本振角频率ωk(k=0,1,…,D-1)由式(4)确定。

图2 实信号滤波器组的低通实现Fig.2 Low-pass filters of real signal

(3)

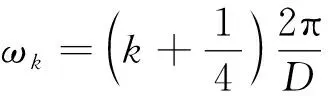
(4)

为了更加有利于工程实现，在原始结构的基础上得到基于多相滤波结构的高效信道化接收结构，推导过程如下。

yk(m)= {[s(n)ejωkn]*h(n)}n=mD=

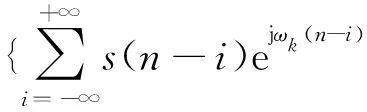
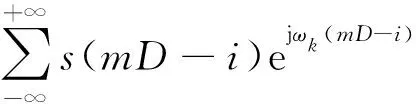
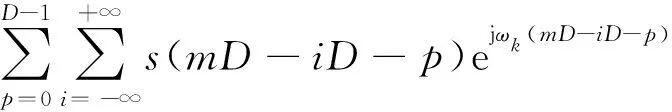
h(iD+p).

(5)

定义：sp(m)=s(mD+p)，hp(m)=h(mD+p)，则有

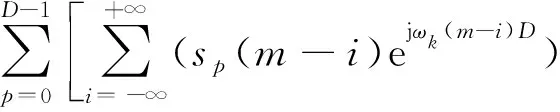
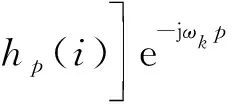
(6)

定义：

[sp(m)ejωkmD]*hp(m),

(7)

代入式(6)可得

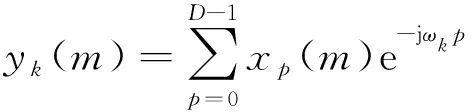
(8)

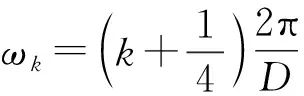
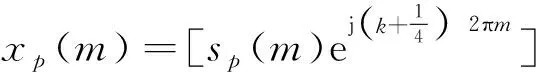
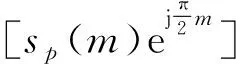
(9)

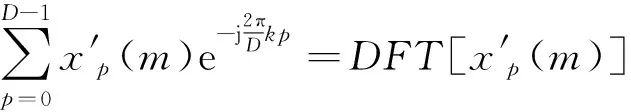
(10)

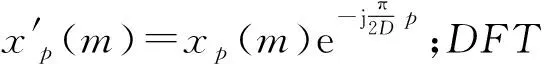
根据以上推导，得到基于多相滤波结构的信道化接收模型如图3所示。

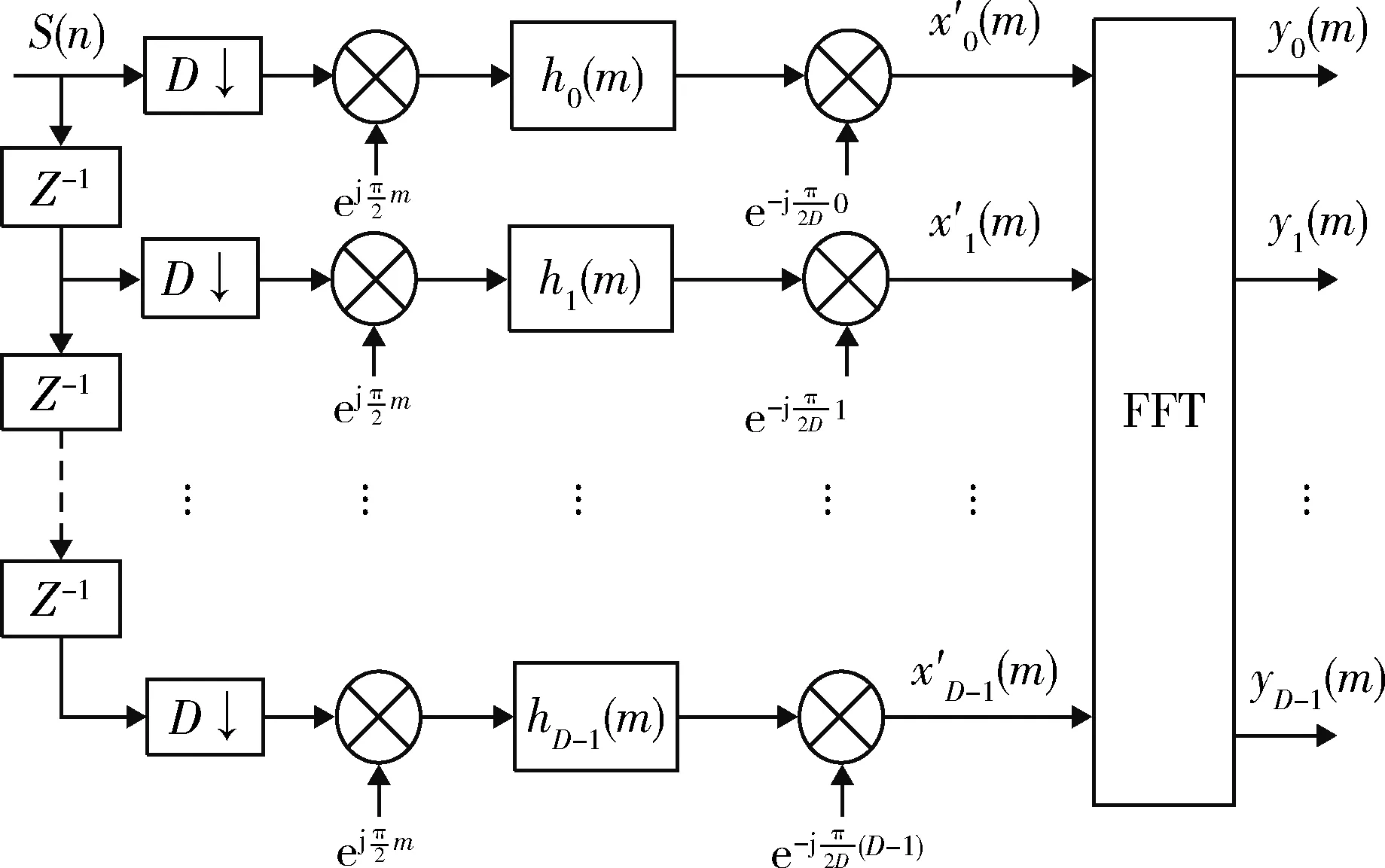
图3 高效信道化接收机结构Fig.3 Construction of efficient poly-phase filter channelized receiver

在以上结构中，系统复杂度和数据速率大大降低，实时处理能力得到提高。该高效结构有如下优点[11-13]：

(1) 各支路共用一个原型低通滤波器，每个信道的原型分析滤波器组是原型低通滤波器hLP(n)的抽样值，抽样值的大小等于信道数的数目，系统设计复杂性下降。

(2) 在求得多相滤波结果的基础上，用DFT一次就可将各支路信号搬到基带上去，不必各信道分别进行下变频计算，提高了计算效率。

(3) 由于采用了多相结构，抽取提在最前面，后续信号的采样率下降，非常有利于后续的硬件处理[14-17]。

2 级联数字下变频方法

为了验证级联数字下变频结构的性能，建立跳频与直扩相结合的宽带快跳频系统的仿真场景，仿真场景的主要指标如下：

跳频频率：3 125跳/s;

跳频带宽：300 MHz;

跳频间隔：3.75 MHz;

扩频码速率：2 MHz;

伪码跟踪精度：1/8 chip。

2.1 ADC采样频率

针对跳频带宽Bs=300 MHz的宽带射频信号，左右预留Bp=180 MHz的保护间隔。设B=Bs+Bp，fs为采样率，f0为中心频率，根据带通采样定理：

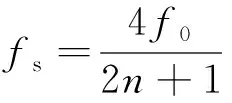
(11)

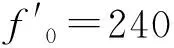
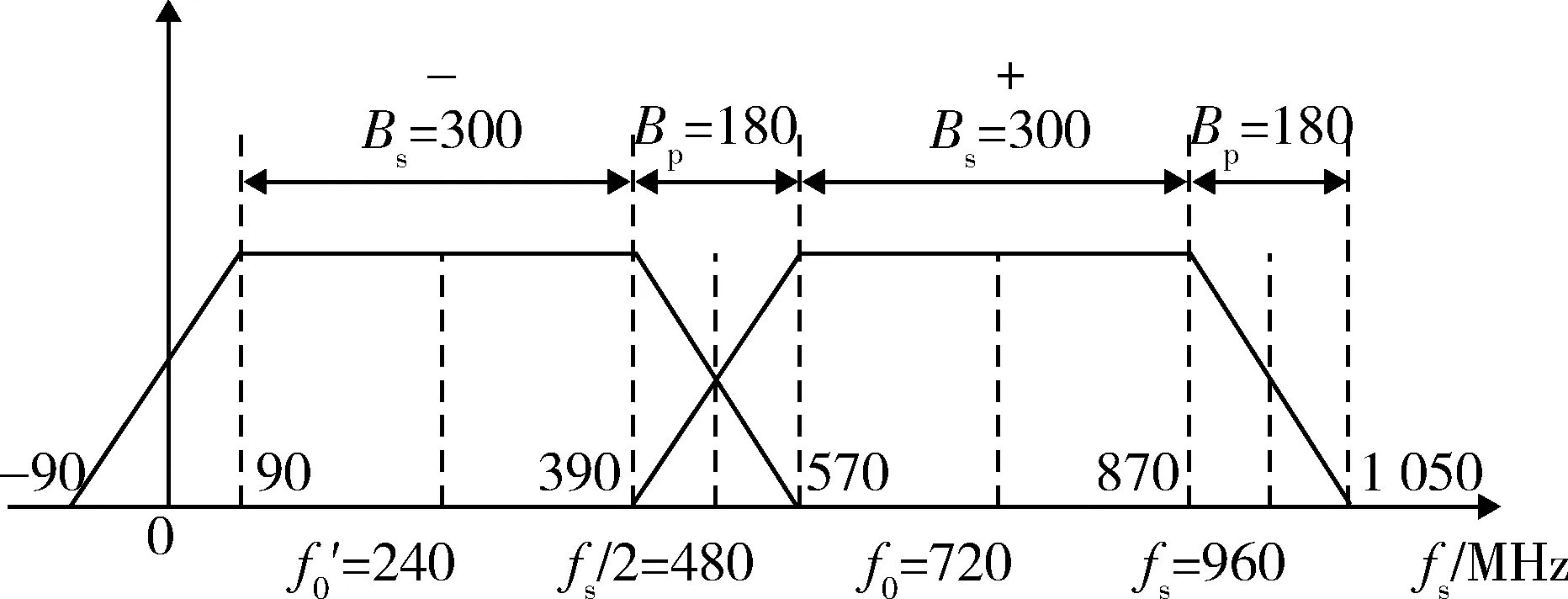
图4 带通采样后宽带信号的频谱示意图Fig.4 Frequency spectrum of wide-band signal after band-pass sampling

2.2 信道化下变频

为了满足“整带抽取”原则，抽取阶数

(12)

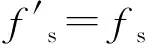
由于采样频率为960 MHz,分析带宽为480 MHz。按3.75 MHz的跳频间隔计算，分析带宽内共包括128个物理信道。取D=32，则每个分析信道包含4个物理信道。其中0～5信道和26～31信道无信号，处于预留保护带内，实际有效信道数为20个。实信号具有频谱对称的特点，占用了一半的频率带宽，为了方便实现高效信道化结构中的DFT过程，用0～2π整个频域来分配信道，中频数字信号的采样频率为960 MHz，每个分析信道带宽为15 MHz，相邻分析信道有1/2的重叠。具体分配情况如图5所示，其中实线表示的主像和虚线表示的镜像交错出现。信道的中心频点ωk表达式如式(4)所示。原型滤波器的通带截止频率为7.5 MHz，过渡带截止频率为15 MHz，FIR阶数为416，分配到32信道中每个信道的滤波器阶数为13阶。

跳频通信系统中需要利用跳频图案同步方式完成接收信号与本地载波的频率同步，同时需要实时补偿载波多普勒误差。信道化过程是一个独立的过程，不受跳频图案影响，不参与跳频图案同步和载波多普勒补偿。相对于数字正交下变频，信道化结构降低了跳频系统数字下变频的实现复杂度，缩短了频率补偿的反馈路径长度，有利于系统调试和稳定性。

2.3 复数下变频

复数下变频结构图如图6所示，输入的数字信号x(n)为复数，分别与本地载波cos(ωkn)和-isin(ωkn)相乘，再经过低通滤波得到复基带信号y(n)，具体的表达式如式(13)～(16)所示。

x(n)=ej(ωkn+θ)，

(13)

x1(n)=x(n)cos(ωkn)=

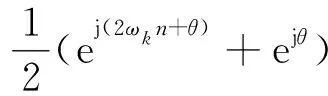
(14)

x2(n)=x(n)(-isin(ωkn))=

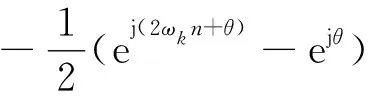
(15)

y(n)=x1(n)+x2(n)=ejθ.

(16)

经过数字信道化处理，32个分析频带被分别搬移至基带。由于每条分析信道包含4个物理信道，且相邻符号使用频点间隔为30 MHz，在解跳时首先选择本地载波跳频频点对应的分析信道支路，再针对其中的某个物理信道进行数字下变频，物理信道与分析信道支路的关系如表1所示。由于此时数据速率已下降为30 MHz，便于复数下变频的工程实现。

复数下变频只需要根据该跳频频点在分析信道的位置，从4个载波频率中选择对应的载波频点号即可。在工程实现过程中4个不同频率的本地载波事先存入ROM中，进一步简化实现结构。跳频信号频点号与复数下变频所需本地载波频率的关系如式(21)所示，其中，i表示频点号，f1,f2,f3,f4为4个复数下变频本地载波频率，Δf(i)为对应于频点号为i的复数下变频本地载波频率。

f1=-5.625 MHz,

(17)

f2=-1.875 MHz,

(18)

f3=1.875 MHz,

(19)

f4=5.625 MHz,

(20)

i∈[1,2,…,80].

(21)

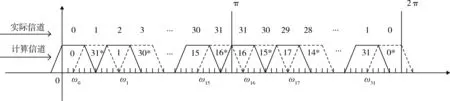
图5 信道的划分Fig.5 Distribution of channels

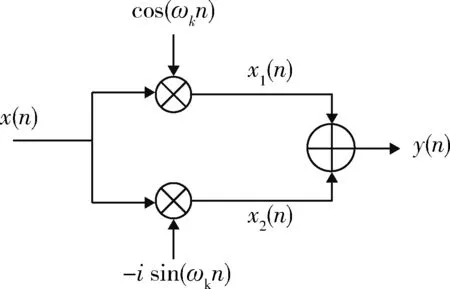
图6 复数下变频结构图Fig.6 Illustration of the plurality down conversion

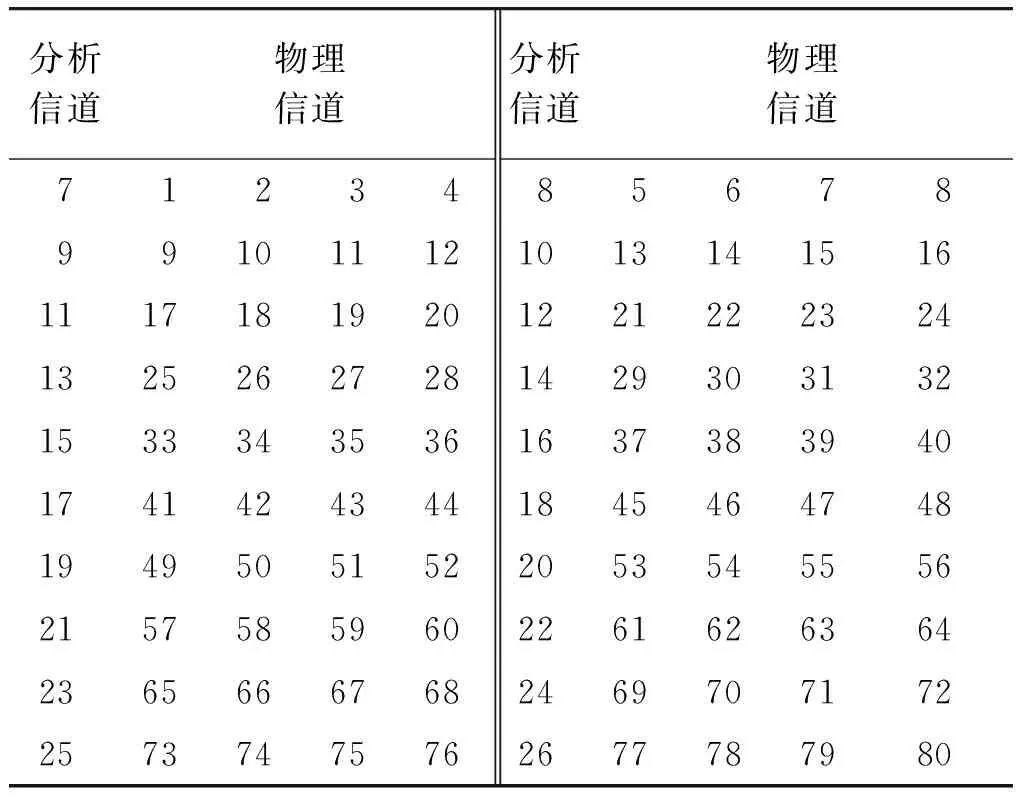
分析信道物理信道分析信道物理信道71234856789910111210131415161117181920122122232413252627281429303132153334353616373839401741424344184546474819495051522053545556215758596022616263642365666768246970717225737475762677787980

3 仿真结果与分析

建立宽带快跳-直扩仿真模型，信号调制方式为MSK调制，扩频码速率为2 MHz,跳频速率为3 125 跳/s。

为了充分验证该方法的有效性，对连续5个跳频频点进行下变频仿真实验，5个跳频频点分别为第38，20，49，70，2号跳频频点。根据物理信道与信道划分的对应关系，上述物理信道分别位于第16，11，19，24，7分析信道内。所在分析信道中心频率的距离即复数下变频的本地载波频率记为Δf(i)，由式(21)可知各个频偏值如下：

Δf(20)=5.625 MHz,

(22)

Δf(2)=Δf(38)=Δf(70)=-1.875 MHz,

(23)

Δf(49)=-5.625 MHz.

(24)

为了便于描述，对跳频频点为38时的12～20分析信道进行观察。12～20分析信道的输出信号频谱图如图7所示，下变频后的信号出现在第16信道，频偏为Δf′(38)=-1.875 MHz，与理论分析一致，且相邻信道的能量抑制在23 dB以上，说明原形滤波器的设计能够满足一般解调时的邻道抑制要求。

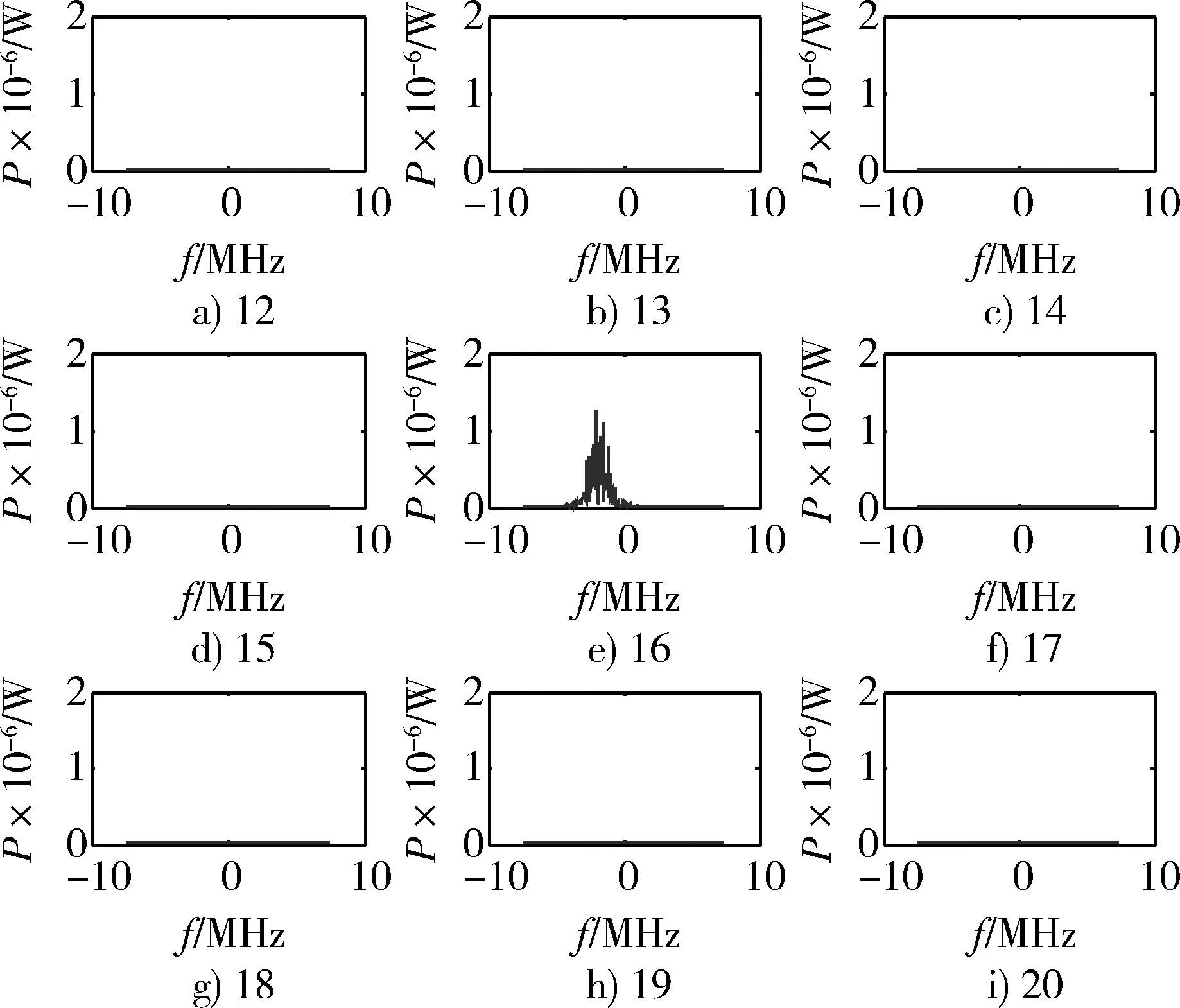
图7 信道输出信号频谱Fig.7 Frequency spectrum of output signal in channel

信道化处理后，当前跳频信号的物理信道距基带还存在一定频偏Δf′(38)。为了得到该信号的基带信号，需要根据频点号进行复数下变频。由于此时信号位于第38个跳频频点上，根据表1知道对应的分析信道为第16个分析信道，因此提取第16个分析信道内的信号进行复数下变频，本地载波频偏值为Δf(38)，最终得到的基带信号频谱图如图8所示。

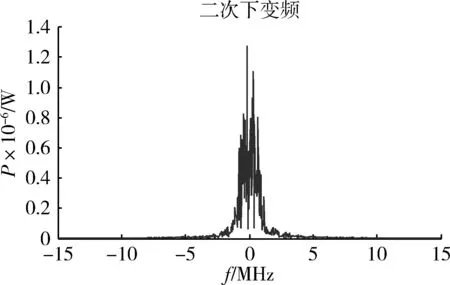
图8 复数下变频输出基带信号频谱(38号频点)Fig.8 Frequency spectrum of baseband signal after the plurality down conversion (the thirty-eighth frequency dot)

最后，对得到基带信号进行解扩与解调，得到的误码率曲线如图9所示。其中x轴表示Eb/N0，y轴表示误码率。由图可以看出，得到的误码率接近理论值。由此可知，本文推荐的级联数字下变频方法未引入运算误差。

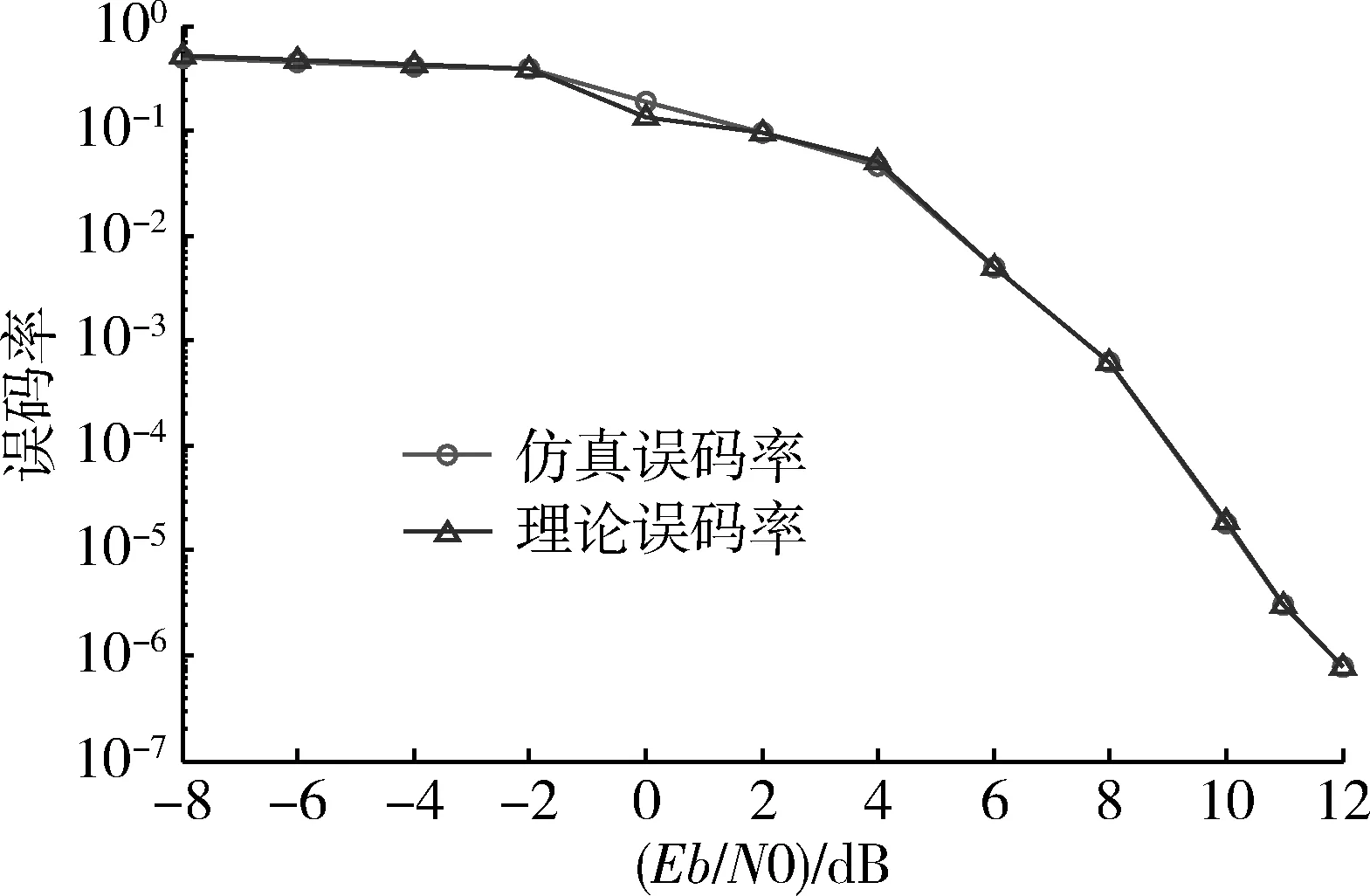
图9 误码率曲线Fig.9 Bit error rate

4 结束语

本文提出一种在跳频通信系统中宽频带级联下变频的方法，该方法采用信道化联合复数下变频的方式实时地实现跳频信号下变频，在该方法中根据跳频同步提供的跳频频点信息提取对应分析信道的输出信号，再进行复数下变频变成基带信号。此级联数字下变频对高速数据进行抽取，降低了功能实现时的系统工作频率，且结构划分清晰，各组成部分耦合度低，功能独立，逻辑运算单纯，并缩短了频率补偿的反馈路径长度，非常适合于直跳扩通信系统的FPGA硬件实现。