多种未来空域窗配置方式下的毁歼效能分析

段修生，王应晨，单甘霖

(1.陆军工程大学，河北 石家庄 050003；2.石家庄铁道大学，河北 石家庄 050003)

0 引言

本文主要分析了目标与未来空域窗相遇时的时间预测误差及位置预测误差对未来空域窗射击体制下高炮毁歼概率的影响，提出通过采用多重未来空域窗以及建立三维的椭球形未来空域区来更有效地毁歼目标，并通过仿真对其有效性进行了分析，为未来空域窗射击体制的实际应用奠定了基础。

1 理想的未来空域窗

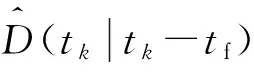
设E为目标相对于预测未来点的弹目偏差，f(E)为弹头的散布密度，如果在预测迎弹面上存在区域W，使得式(1)成立：

(1)

则定义W为理想未来空域窗。

在预测迎弹面内以目标预测提前点Mq为原点，建立二维直角坐标系Oxy，y轴为包含预测弹丸存速方向的铅锤面与预测迎弹面的交线，正向朝上；x轴垂直于y轴，正向指向航路方向，如图1所示。

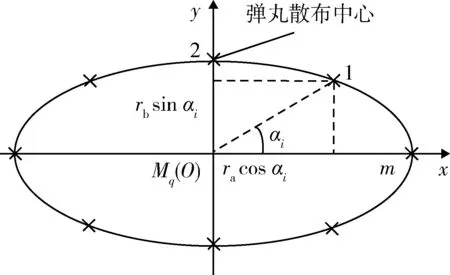
图1 未来空域窗原理Fig.1 Principle of future airspace window

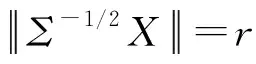
古代有学者就有“温故而知新”这一说法。其实，我们体育教师可以在新旧知识、技术、技能之间架起一座桥梁，使学生在“温故”之时，导入以旧引新，学新联旧、新旧类比。如：水平二的《前滚翻》教学时，我们可以在准备活动中复习各种滚翻练习，引出团身这一要点，为新授前滚翻技术服务。这种以旧引新的方式是我们教师常用的形式，在学生已有的知识、技术、技能的基础上，充分利用学习的正迁移，循序渐进地顺势延伸过渡。

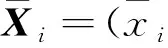
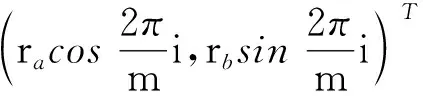
(2)

在文献[15]中已证明：可构成一个在弹丸配置中心区域保持平坦性的椭圆形未来空域窗。(ra,rb)称为射击窗技术参数，若ra=rb，则构成圆形未来空域窗。当射击窗技术参数确定后，弹丸散布方差Σ也随之确定。

2 多重未来空域窗配置方式

2.1 时间误差对毁歼效果影响

设在t=0时刻向目标射击，如果弹道解算和目标航迹预测都没有误差，那么以未来空域窗射击体制配置的所有弹丸，将在t=tf时刻到达预测迎弹面，构成未来空域窗W，与此同时，目标也刚好到达未来空域窗的几何中心O，即目标预测未来点，未来空域窗能够有效地毁歼目标。但在实际作战过程中，由于目标机动情况的变化以及复杂环境对实际弹道的影响等因素，往往会存在一定的时间预测误差，目标有可能会超前或滞后于t=tf时刻与未来空域窗相遇。在提前或滞后于t=tf的时间较短的情况下，由于目标和未来空域窗之间存在非平行的相对运动，二者还是会在某一时刻相遇，未来空域窗依然可以对目标进行毁歼；然而，如果目标提前或滞后到达未来空域窗的时间过长，目标与未来空域窗将不能再相遇，未来空域窗不能有效毁歼目标。此时，可以通过在目标预测航迹上按一定间隔同时设置多重未来空域窗，以保证至少有一个未来空域窗与目标相遇，来确保能够有效对目标进行毁歼。

2.2 多重未来空域窗的构造

为了尽可能地使得运动的未来空域窗与机动目标相遇，必须对多重未来空域窗的间隔进行设计。设目标提前到达时间为ta，目标滞后到达时间为tl，定义允许目标滞后时间tl与允许目标提前时间ta之和称为未来空域窗对目标的有效作用时间，记之为tw；定义在未来空域窗对目标有效作用时间内，弹头运动距离称为未来空域窗的有效作用距离[13]。如果在tw时间内目标与未来空域窗不能相遇，则应沿目标预测航迹即目标预测速度矢量vt，平行于预测迎弹面同时建立多个未来空域窗，未来空域窗之间的间隔应小于未来空域窗的有效作用距离。

多重未来空域窗可以通过2种方法来构建：建立2i-1和2i个未来空域窗，其中，i为正整数，分别如图2和图3所示，图中vt和vb分别为目标和弹丸速度。前者在预测迎弹面上，以目标预测未来点为中心，设置一个未来空域窗，再沿弹丸预测存速方向平行于预测迎弹面等距离地分别设置i-1个未来空域窗；后者则同样平行于预测迎弹面等距离地分别设置i个未来空域窗。

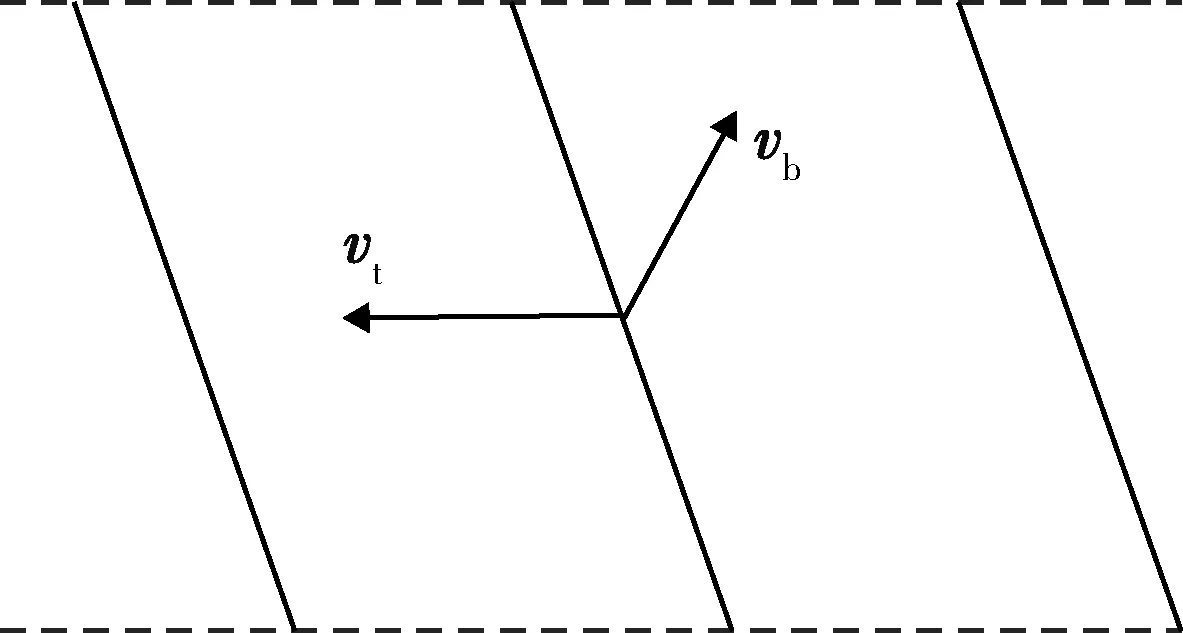
图2 三层未来空域窗Fig.2 Three-layer future airspace window

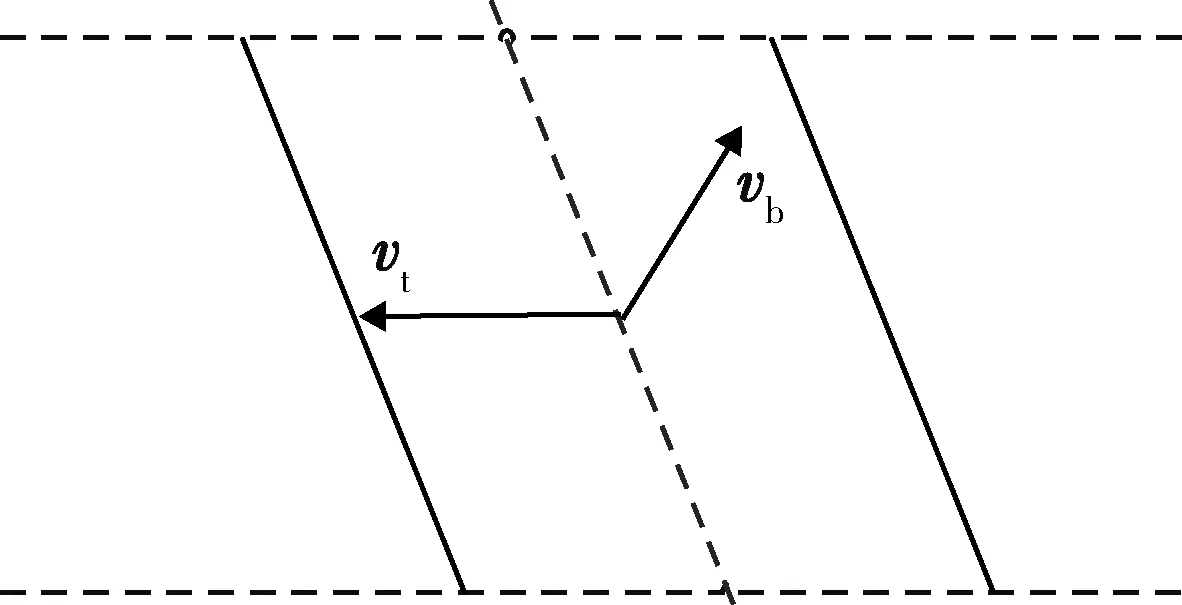
图3 两层未来空域窗Fig.3 Two-layer future airspace window

3 椭球形未来空域区

3.1 目标位置预测误差

目标到达预测迎弹面时的实际位置与预测位置存在偏差，称为目标位置预测误差，其影响因素如下：

(1) 测量误差：测量误差主要指由于雷达等观测设备存在误差而产生的误差，包括距离误差、方位角误差及高低角误差。

(2) 目标运动假设误差：由于在火控解算的过程中，一般假设目标作匀速或匀加速直线运动，而目标为了躲避防空武器的袭击，往往会进行一定的蛇形机动来保证自身安全，在这种情况下，对目标运动模型假设误差会使目标到达未来空域窗的位置以及目标预测未来点产生一定的误差。

在预测迎弹面与实际迎弹面的中心的位置、弹丸预测存速与弹丸实际存速的方向均相近时，为方便计算，在空中只需形成二维的未来空域窗。然而，在目标实际位置预测误差较大的情况下，则需形成三维的未来空域区。如图4所示，目标未来点在时间上服从一维正态分布，主要分布在x3轴上，在空间位置上服从二维正态分布，主要分布在预测迎弹面Ox1x2内。因此，未来空域区为服从三维正态分布的时空域，可用三维正态分布的3σ等概率椭球所包含的空域描述，该空域为椭球域。

3.2 未来空域区的毁歼概率

未来空域区的数学模型可表示为

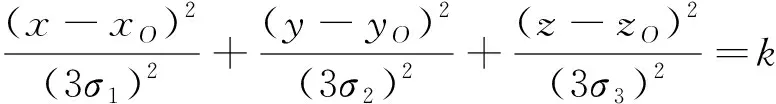
(3)

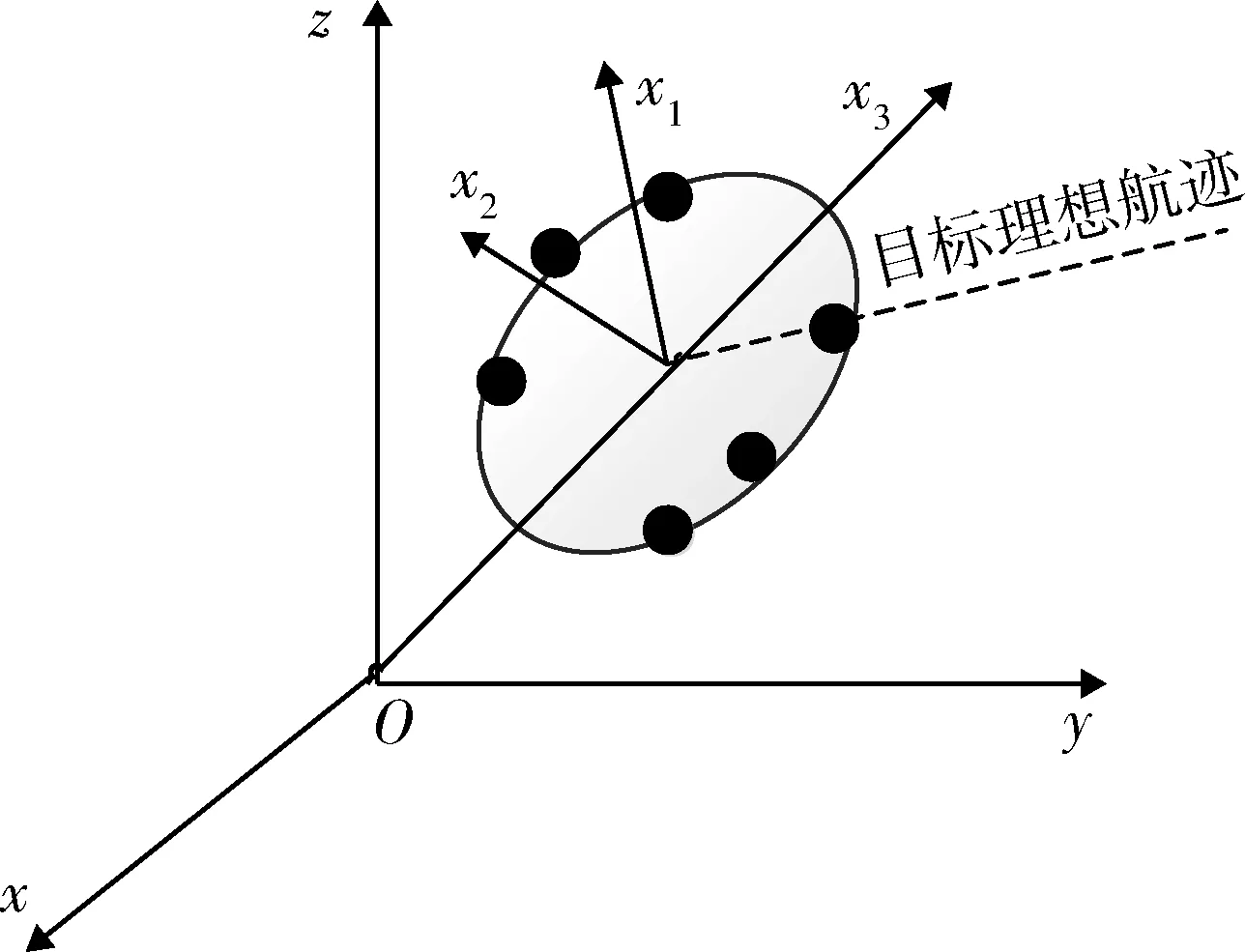
图4 椭球形未来空域区Fig.4 Ellipsoidal future airspace district

目标未来点在未来空域区内出现的概率密度函数为

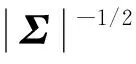
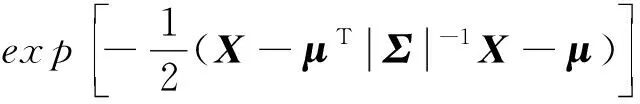
(4)

式中：X∈[μ-3σ,μ+3σ]，

则未来空域区下高炮对目标毁歼概率为[16]

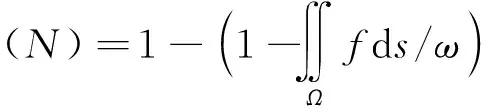
(5)

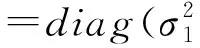
4 仿真算例

4.1 仿真条件

4.1.1 目标及其航路相关参数

目标航路倾斜角λ=0，目标飞行速度vt=300 m/s，蛇形机动幅度为10 m，飞行高度h=1 000 m，航路捷径dj=1 000 m，航程s=5 000 m。

4.1.2 某型高炮火控系统相关参数

毁歼目标平均所需的命中弹数ω=3，椭圆形未来空域窗参数ra=4 m，rb=10 m，x轴弹丸散布误差均方差为2.82 m，y轴弹丸散布误差均方差为7.07 m，弹丸散布中心m=8，弹丸存速vb=900 m/s，每个弹丸散布中心射击弹丸数n=20。在多重未来空域窗射击方式下，采用三层未来空域窗配置方式，未来空域窗间隔10 m；在椭球域未来空域区射击方式下，沿弹丸存速方向椭圆半轴长为10 m。由于目标位置预测误差与时间预测误差及目标速度有关，在目标速度一定的情况下，只需分析目标位置预测误差即可得出与时间预测误差相同的结论。目标位置预测误差设定为[1 10]m。

4.2 仿真结果

仿真结果如图5所示。

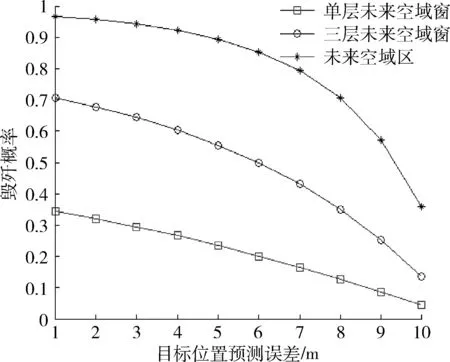
图5 目标位置预测误差对毁歼概率影响Fig.5 Influence of target position prediction error on kill probability

分析图5中的仿真结果，可以得出以下结论：

(1) 在同一类型未来空域窗配置方式下，随着目标位置预测误差的增大，高炮对目标毁歼概率逐渐减小，这一结论与理论分析所得的结论相同。

(2) 在目标位置预测误差相同的情况下，采用椭球形未来空域区配置方式时高炮对目标毁歼概率最高，三层多重未来空域窗配置方式次之，单层未来空域窗配置方式最低。这是由于在单层未来空域窗配置方式下，目标难以与未来空域窗相遇在目标预测未来点，毁歼概率较低；在三层多重未来空域窗配置方式下，能够确保有未来空域窗对目标形成阻拦，有更高的毁歼概率，但是会造成弹丸的浪费；在椭球形未来空域区配置方式下，未来空域区内弹丸散布密度更加均匀，而且在预测弹丸存速方向充分配置了一定的弹丸数，很好地减小了目标时间预测误差及位置预测误差带来的影响，有更高的毁歼概率。

5 结束语

本文主要分析了目标与未来空域窗相遇时的时间及位置预测误差对未来空域窗射击体制下高炮毁歼概率的影响，提出了采用多重未来空域窗配置方式和三维椭球形未来空域区配置方式，来减小预测误差对高炮毁歼效能带来的影响，并以毁歼概率为指标对几种配置方式下的毁伤效果进行了分析。仿真结果表明，椭球域未来空域区配置方式毁伤效能最好，多重未来空域窗配置方式次之，两者都减小了时间及位置预测误差带来的影响。研究符合实际作战背景，为未来空域窗射击体制的实际应用奠定了基础。