磁性目标跟踪的多模型自适应滤波方法

张宏欣

（中国人民解放军91439部队43分队，辽宁 大连116041）

0 引言

水中舰艇目标在空间中能够产生叠加于当地局部地磁场之上的稳定感应磁场，利用水下测量平台测得的目标相关磁信号，基于磁场数学模型，采用相应的求解方法，获得目标相对于水下平台的位置，速度及磁特征参数，这对于水中兵器目标定位、掩埋爆炸物探测定位以及医疗探查等[1–3]应用具有重要意义。

磁偶极子跟踪问题主要有解析反演[4]、离线寻优[5]以及滤波估值[6-7]三类求解方法。滤波方法由于能够从带噪观测数据中实时估计目标状态，因此得到了较为广泛的研究。采用滤波方法进行磁偶极子跟踪的主要困难在于高维、强非线性条件下的滤波初始条件不易确定，而初始条件恰是决定磁偶极子跟踪性能的关键因素[8]。粒子滤波[9]虽然能够克服非线性问题，但其所需的粒子数量仍然随着问题维数规模的扩大呈几何级增长[10]，故基本的粒子滤波方法无法用于磁性目标实时定位问题，目前已有文献采用了卡尔曼滤波方法来建议分布抽样，再进行重采样的解决方案，但在实时应用时计算量仍过大，且在权值计算中需要很高的数位精度，这对于实际实现也是不利的。

对于磁性目标跟踪而言，无论是批量求解方式或序贯递推方式，其结果好坏极大程度地依赖于初始条件，包括目标位置初始和源强度（磁矩）的选取，由于两者必须同时确定，故求解初值相当于求解跟踪问题本身。为此，本文提出一种基于静态多模型滤波思想的自适应跟踪方法。首先通过对观测模型进行分析，设计了一种磁性目标初始参数估算方法，通过该方法得到不同假设条件下的磁性目标状态初值及其误差矩阵。在此基础上，以EKF作为基本单元，对每个初值起始一个滤波器进行求解，根据各个滤波器的求解结果，利用最大似然准则进行选取，选取的滤波器对应的估计结果即可作为当前时刻的状态估计值。通过设计仿真实验对本文方法的有效性进行了验证。

1 问题模型与求解

由于水中目标运动是低动态的，其航迹可用线性动态模型描述，则问题模型为

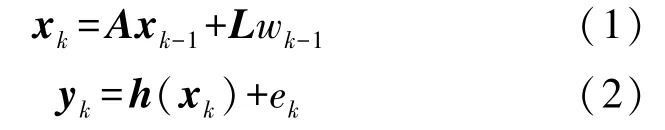
式中：A为状态转移矩阵；h（·）为观测方程；L为过程噪声权重系数矩阵；wk－1，ek分别为噪声协方差矩阵Qk－1和Rk状态噪声和观测噪声，且Qk－1＝。

式中：O，I分别为相应维度的0矩阵和单位矩阵；TS为采样时间。

状态向量xk由以下状态分量构成

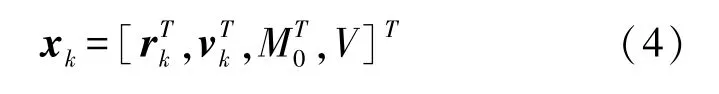
式中：rk，vk，M0分别为目标位置、速度和磁矩矢量；V为目标体积系数。

根据磁偶极子模型等效，观测方程表达式为

式中：mk＝RZ（vk）M0＋V／μ0·B0为考虑软铁磁化和硬铁磁化的总磁矩；μ0为水中的磁导率；M0为目标硬铁磁矩矢量；B0为背景磁场矢量。RZ为以速度为参数的绕z轴方向的旋转矩阵，此时式（2）中的ek即为环境磁场噪声矢量。联合式（1）-（5）即可构成磁性目标跟踪问题的状态空间模型，从而可利用非线性滤波方法对目标状态进行求解。

考虑静态多模型方法对问题进行求解，其主要思想是假设整个滤波估值过程中真实系统模型不发生变化，且服从个候选模型中的一个

根据贝叶斯定理，在给定当前观测值序列y1∶k条件下，候选模型为真实模型的后验概率

多模型估计的后验分布p（xk丨y1∶k）为混合高斯分布，即

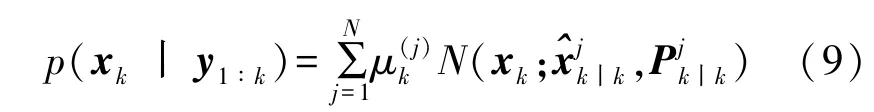
假设真实初始状态在状态空间中呈均匀分布，则每个假设初始状态可视为一个模型，即

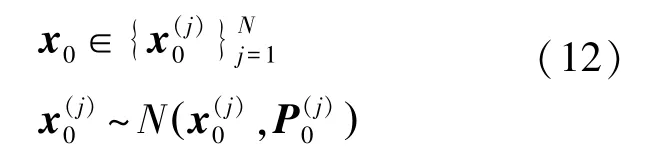
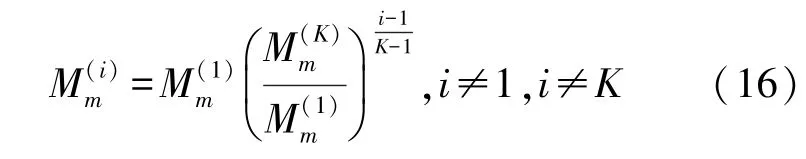
式中：Mm（1）可利用式（14）计算已知深度条件下产生给定信噪比信号的磁矩模来给出；Mm（K）则可以取大型舰船目标通常的经验磁矩强度的2～5倍。

在确定Mm（i）之后，将Mm（i）代入式（15）即可估算出在每个假设目标源强度条件下的水面目标初始距离，至此便获得了K个可能的目标初始距离，再利用前述的过程（即每个距离上起始多个滤波器）进行多初值模型估计。

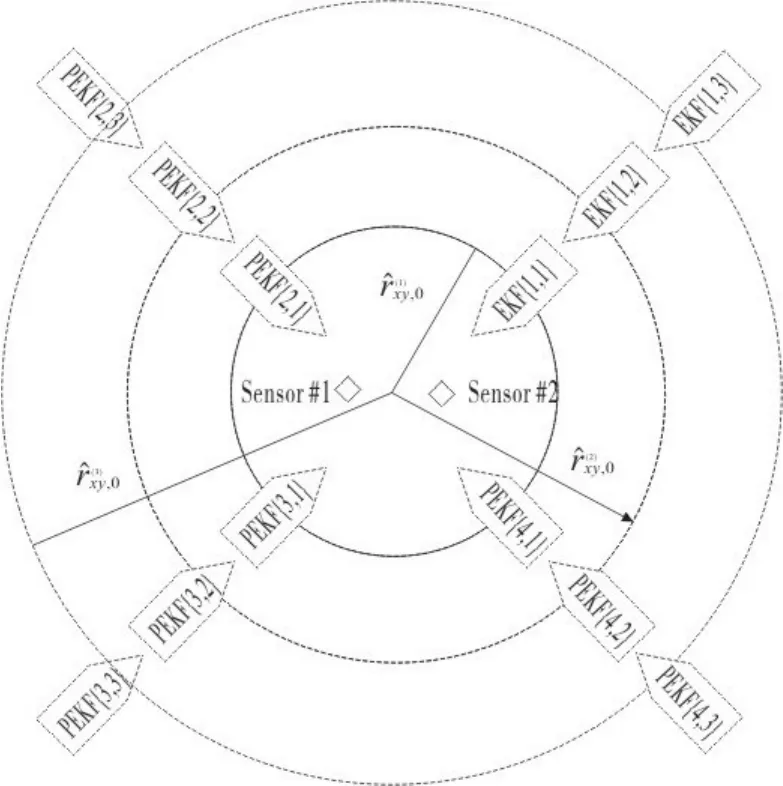
图1 目标初始位置的多初值模型设计Fig.1 Multiple initialization model design for initial target position

图2 估算距离误差的（拟合）概率分布Fig.2 （Fitting） Probability distribution of estimated distance errors

图1中给出了假设距离数K＝3，每个距离上等方位间隔地起始4个PEKF滤波器条件下的多初值模型设计，其中 EKFi，j，i＝1，2，…，K，j＝1，2，…，NF，NF为每个初始距离上起始的滤波器数量。则各个初值模型参数，即PEKFi，j的初始状态（i，j）0为

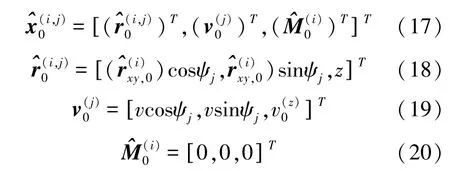
相应地，初始误差矩阵P（i，j）0为

式中：ψi为假设的目标方位角；状态误差矩阵由位置误差矩阵、速度误差矩阵以及磁矩矢量误差矩阵组成；位置与磁矩矢量的误差矩阵由估算值近似地给出，以使得误差范围能够包括真实状态。注意由于不同目标的磁化情况差异，各磁矩分量的正负号不定，因此其初值均为0。此外，式（22）和式（23）中的ξz，ξvz分别为 Z 轴方向目标位置误差，可由已知深度、测深误差及目标吃水情况来确定；ξvx，ξvy，ξvz分别为X，Y，Z轴方向速度分量误差，v与v（z）0分别为XOY平面速度模值和Z轴方向速度分量，这些量可通过目标舰速的经验范围来确定。

对于多初值模型而言，加权融合方式会产生多滤波器的“竞争”效应，随着初值模型的增加反而会降低整体滤波性能，因此，本文下面采用最大似然选择算法来选取最佳估计值。

首先根据式（7）给出的递推公式可得

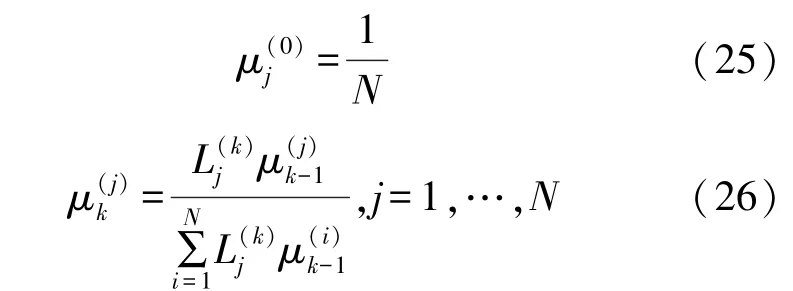
根据上式可知，由于各模型先验概率是相等的，则可将式（26）重写为

由于k时刻的归一化操作不会改变分子项的相对大小，因此最大似然选择算法可直接利用似然函数进行判别，故对似然函数取对数

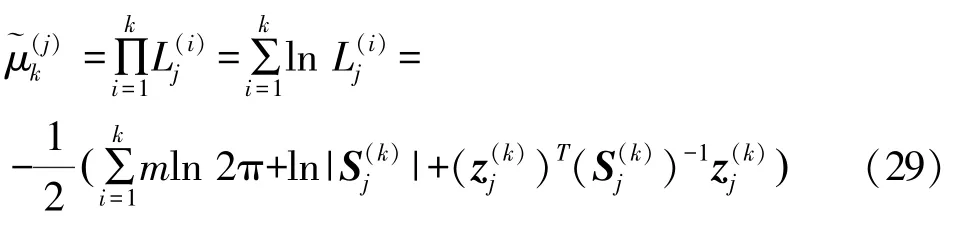
为避免量级上的过度增长，利用各模型中的最大似然值进行归一化

综上，可给出磁性目标的MIM-EKF跟踪算法步骤如下：

1）确定假设目标距离数K及每个距离上起始的滤波器数量NF，确定滤波器的初始条件。

2）从k＝1时刻开始，对每个初值模型进行EKF滤波，得到各滤波器输出，其中残差及其协方差矩阵在观测更新之前给出。

3）利用式（29）更新权值得到当前时刻各初值模型的似然值。

4）输出k时刻最大似然选择的滤波器结果，且

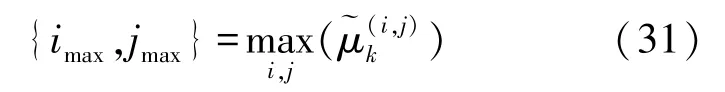
5）利用式（30）对似然值进行归一化。

6）回到步骤2或终止滤波。

2 仿真结果及分析

本小节利用磁偶极子三维运动模型来设计数值仿真实验，以验证前述提出的MIM-PEKF算法，考察算法在先验信息缺失条件下的有效性。

考虑如表1所示参数的水面目标跟踪仿真跟踪场景，其中Oi，i＝1，2为2个三轴磁传感器所在观测点的位置，H0＝50为观测点深度，r0，v0分别为目标位置和速度的真实初始值，M0为磁矩矢量，σq＝0.1，σr＝8分别为过程噪声与观测噪声强度。TN为仿真观测点数，Ts为采样时间间隔。

对于MIM-PEKF滤波器配置，假设目标源强度分布在K＝3个数量级上，即Mm（1）＝104，Mm（2）＝105和Mm（3）＝106，采用本文给出的初始参数近似确定方法，拾取SNR＞12.5 dB时的两传感器测量数据参与初值近似计算，得到3个可能的目标平面初始距离。在各个距离上起始NF等于4个PEKF滤波器，各个滤波器的假设方位分别为 π／4，3π／4，5π／4，7π／4，根据式（17）-（24）确定出各个滤波器的初始条件。总的滤波器数量为K·NF＝12。

表1 仿真场景参数设置Table 1 Parameters setting for simulation scenario

图3 目标运动参考轨迹Fig.3 Reference trajectory of target motion

图4 前4个最大似然值初值模型跟踪结果Fig.4 Tracking results of first 4 initialization models of maximum likelihood value

图3给出了在表1参数条件下的目标运动参考轨迹；图4给出了对于该轨迹，对数似然值最大的前4个初值模型的跟踪结果，可见这4个初值模型都处于与真实情况相近的方位范围，这说明相比距离而言，磁性目标跟踪误差对方位先验信息更加敏感。

给定以上仿真场景参数和初始条件设置，采用本文算法进行100次Monte-Carlo运算，根据估计结果中的每个初值模型条件下的滤波结果，统计其总均方误差（totalrootmean square error，TRMSE），定义为

式中‖·‖2为矢量模运算。

图5 各个初值模型滤波的总均方误差与对数似然值的一致性对比Fig.5 Comparisonof consistency between TRMSE and log-likelihood value for each initialization model filtering

图5给出了各个滤波器经100次Monte-Carlo计算后统计的平均对数似然值.对比两图可知，显然对数似然值最大时所对应的滤波器与TRMSE值最小时对应的滤波器是一致的（i＝11）.这说明本文的最大似然选择方法确能够选择出最小RMSE误差对应的滤波器.

3 结束语

本文针对非协作磁性目标跟踪中目标先验信息缺失导致的初值难以确定的问题，提出一种基于静态多模型的自适应滤波方法。基于静态多模型框架重点研究了多初值模型的参数确定问题，并给出了一种参数估算方法，通过仿真结果验证了本文方法的有效性，表明该方法可在目标源及位置等先验信息完全未知条件下准确估计出真实目标状态，对磁性目标实际应用具有参考价值。需要说明的是，本文方法相比单模型处理而言增加了复杂度，下一步将对解决起始大量模型滤波时存在的空时复杂度及并行滤波处理问题做进一步分析和研究。