CT系统参数标定及图像重建模型
2018-10-26高雅倩
高雅倩


摘 要:当今,CT系统被广泛应用于医疗与工业生产中。精确的几何参数标定和准确的图像重建方法是CT系统研究课题中的重要任务。本文以2017年高教社杯全国大学生数学建模竞赛A题为例,依据Radon变换和最小二乘方法,经过坐标变换,建立优化模型求解出系统的旋转中心、初始角度和探测器间距。基于所求参数,采用滤波反投影算法,通过平移及旋转修正完成图像的重建。
关键词:CT系统 参数标定 图像重建 Radon变换 滤波反投影算法
中图分类号:TP39 文献标识码:A 文章编号:1672-3791(2018)04(c)-0088-03
1972年Hounsfield研制出第一台CT机。40多年来,CT技术在其扫描方式、成像视野、重建速度、重建图像质量以及应用领域等方面都得到了飞速发展 [1]。
在实际应用中,CT系统的参数由于安装不当等原因会产生一定的误差,由误差引入的几何伪影极大地影响重建图像的质量。本文借助结构已知的模板,依据CT系统的成像原理,建立数学模型求系统参数的精确值,再将计算结果作为已知条件,把“取投影”→“反投影重建”→“重建后的图像”这一过程看作一个输入原像,输出重建图像的成像系统[2],建立反投影图像重建模型来反演出介质的形状和坐标系中的位置。
1 模型的建立与求解
1.1 基本假设
假设一:假设X射线由单一能量的光子组成。
假设二:假设X射线源焦点的物理尺度可以忽略,可视为理想的几何点。
假设三:假设探测器单元的物理尺度可以忽略,可视为理想的几何点。
假设四:假设CT系统每次旋转的角度是均匀的。
1.2 CT成像原理与Radon变换
本文给出的CT系统是从初始位置起,扫描完一个指定层面后,系统转过一个角度(一般为1°),然后对同一指定层面进行扫描,如此进行下去直到扫描系统与初始位置成180°的位置。CT系统的旋转示意图及坐标系如图1、图2。
由于我们的模型是以正方形托盘来建立坐标系的,因此必须对Radon逆变换后的结果做旋转校正,将介质在坐标系中旋转角度φ0。同时,依据坐标变换做一逆向变换,也就是将介质的几何中心平移到坐标系的中心处。
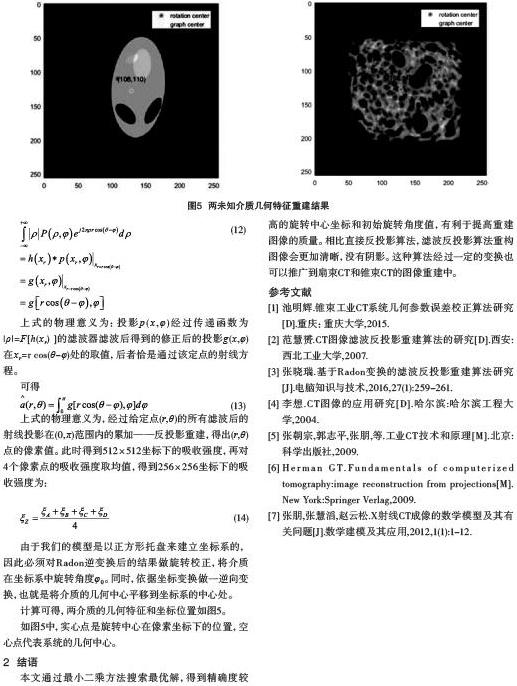
计算可得,两介质的几何特征和坐标位置如图5。
如图5中,实心点是旋转中心在像素坐标下的位置,空心点代表系统的几何中心。
2 结语
本文通过最小二乘方法搜索最优解,得到精确度较高的旋转中心坐标和初始旋转角度值,有利于提高重建图像的质量。相比直接反投影算法,滤波反投影算法重构图像会更加清晰,没有阴影。这种算法经过一定的变换也可以推广到扇束CT和锥束CT的图像重建中。
参考文献
[1] 池明辉.锥束工业CT系统几何参数误差校正算法研究[D].重庆:重庆大学,2015.
[2] 范慧赟.CT图像滤波反投影重建算法的研究[D].西安:西北工业大学,2007.
[3] 张晓瑞.基于Radon变换的滤波反投影重建算法研究[J].电脑知识与技术,2016,27(1):259-261.
[4] 李想.CT图像的应用研究[D].哈尔滨:哈尔滨工程大学,2004.
[5] 张朝宗,郭志平,张朋,等.工业CT技术和原理[M].北京:科学出版社,2009.
[6] Herman GT.Fundamentals of computerized tomography:image reconstruction from projections[M].New York:Springer Verlag,2009.
[7] 張朋,张慧滔,赵云松.X射线CT成像的数学模型及其有关问题[J].数学建模及其应用,2012,1(1):1-12.
