铜氧化物超导体 Bi2Sr2CaCu2O8+δ多体相互作用的超高能量分辨和时间分辨角分辨光电子能谱研究
2018-10-25周超成张文涛
周超成,张文涛
上海交通大学物理与天文学院,上海市闵行区东川路800号,200240
目 录
I.研究历史及进展200
II.超高能量分辨角分辨光电子能谱对多体相互作用的研究 201
A.节点区的研究 202
B.反节点区的研究 203
C.相互作用的动量依赖关系 204
D.配对电子自能的提取 205
III.时间分辨角分辨光电子能谱对多体相互作用的研究 208
A.节点区的研究 208
B.动量依赖关系 209
C.玻色子的受激辐射 212
IV.讨论总结 215
致 谢 215
参考文献 215
I.研究历史及进展
铜氧化物超导体的超导机理一直是凝聚态物理学的研究热点。由于其内部电子与其他粒子或准粒子之间的强相互作用,其正常态的电子运动行为并不能用传统的费米液体理论来解释,在传统超导体中已经显得十分完善的 BCS理论在铜氧化物超导体上并不适用。其高温超导机理及有关物理问题比如赝能隙、相图的研究是强关联乃至整个凝聚态物理研究领域极为重要的问题。虽然其机理问题至今仍未解决,但经过科学家几十年的不断攻关研究,对高温超导体机理及相关物理问题的认识已经大大深化。角分辨光电子能谱(angle-resolved photoemission spectroscopy,ARPES)作为研究固体电子结构最直接的实验技术,能够直接提供单粒子谱函数A(k,ω)的信息,在过去近三十年中对这些问题的研究起到了无可替代的作用[1]。

图1.TrARPES原理示意图[2]
时间分辨技术是最近兴起的研究热点,其利用超短脉冲激光作用在固体材料上产生新奇的非平衡态量子现象,比如光致非平衡超导[3−5]、光致超快相变[6−12]、 光致新的物理相[13−15]等。光学时间分辨技术比如时间分辨光学反射、透射实验技术在这些相关研究中发挥了重要作用,但是仅用光学的时间分辨技术无法直接探测产生的准粒子或得到材料内部关于动量的信息,从而只能间接地获得电子自能、非平衡态的多体相互作用等信息[16]。近年来兴起的时间分辨角分辨光电子能谱(time-and angleresolved photoemission spectroscopy,trARPES)是在现有的ARPES技术上发展起来的一种探测固体中电子态超快过程的新型实验手段[17−20]。与常规ARPES不同的是,trARPES一般使用两束脉冲长度为飞秒(fs)至皮秒 (ps)量级的脉冲激光光源,一束红外泵浦激光脉冲将样品电子态激发到非平衡态,另一束深紫外激光脉冲经过给定的时间间隔后进行光电效应探测,并通过改变两种脉冲之间的时间间隔来实现时间分辨 (图1)。 通过探测不同时间间隔下的瞬态电子结构,即可获得随时间演化的单粒子谱函数A(k∥,ω,t)。TrARPES可以追踪电子结构随时间的演变,提供相关准粒子寿命和特征能量以及由电子–电子和电子–声子相互作用产生的时间尺度信息,从而为研究材料中的相变以及超导产生机理提供重要信息。同时它兼具单光子光电子能谱和反光电子能谱的优点,能够同时探测占据态和非占据态的信息,使得其成为电子动力学领域最有力的实验手段之一。
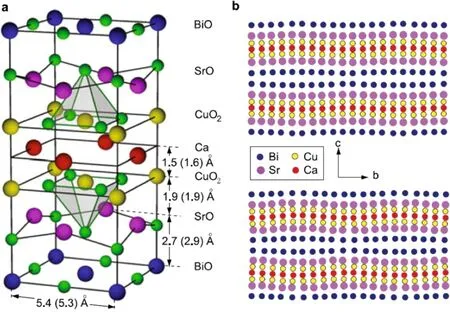
图2.Bi2212样品的晶体结构及超结构示意图[21]
自 1988 年,Bi系铜氧化物超导体 Bi2Sr2CaCu2O8+δ(Bi2212)发现以来[22],绝大部分对高温超导体的ARPES研究都集中在Bi2212样品上。作为空穴型掺杂超导体,Bi2212的晶体结构为典型的二维钙钛矿型结构(图2(a)),顶部Bi-O层为电荷库层,提供导电所需的载流子;其下为Sr-O层;再往下是两层Cu-O2面为导电层,在两层Cu-O2面之间夹着一层 Ca原子起到调节载流子浓度的作用。在 Bi2212样品中存在着超结构,即一个单胞由两个图示的结构沿晶体a或b方向错开半个晶格常数并在 Bi-O层之间组合而成。Bi-O层之间的范德瓦尔斯结合力很弱,解离时样品首先从Bi-O层处断开,形成一个无极化的样品表面。密度泛函理论计算和X射线衍射实验证明其在b方向,即与 Cu-O键成 45◦的方向存在一个约为 4.8个单胞的周期(如图2(b))[21]。根据 Laue单晶衍射实验可以判断出超结构方向,其中超结构方向对应着广泛研究的倒空间中节点方向。此外,Bi2212有很高的超导转变温度,根据掺杂浓度的不同,在掺杂浓度约为 0.16时可达最高超导转变温度约91 K,此时称为最佳掺杂 (Optimally doped,OP);掺杂浓度大于 0.16时称为过掺杂 (Overdoped,OD);掺杂浓度小于 0.16时称为欠掺杂 (Underdoped,UD)。其超导转变温度随着掺杂浓度偏离最佳掺杂而逐渐减小。总的来说,Bi2212有易解离、超导转变温度高、掺杂范宽以及有准二维性等特点,十分适合 ARPES研究,是ARPES研究高温超导电性的重要材料之一。本文以下介绍均是基于Bi2212样品的研究。
II.超高能量分辨角分辨光电子能谱对多体相互作用的研究
材料的物理宏观性质是由具有多体效应的电子的微观动力学所决定的,这些多体效应包含了电子和其它电子、声子、磁振子、杂质等其他集合模式之间的相互作用。对这些多体相互作用的探测与研究对于理解和解释宏观的物理现象有着重要的作用。高分辨的角分辨光电子能谱作为研究多体效应的有效手段在铜氧化物超导体中有众多的应用与发现。铜氧化物超导体中电子结构和超导能隙均有强烈的各向异性,节点区与反节点区的电子结构、超导能隙有着很大的差异。因此,研究多体相互作用的动量依赖关系对理解高温超导机制非常重要。
A.节点区的研究
节点方向如图3中红色箭头所示,是指在布里渊区中 Γ(0,0)−Y(π,π)方向。铜氧化物超导体中出现的超导能隙与“赝能隙”等物理现象在节点区域与反节点区域(图3中黑色圆圈)表现的截然不同,在节点区有着超导能隙与赝能隙均为零等独特的现象[1]。因此,节点区与高温超导是否存在关联吸引着人们广泛的研究。
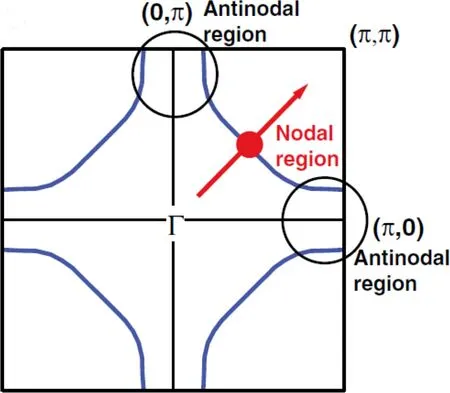
图3.节点反节点区域示意图[23]
图4(a)为最佳掺杂Bi2212样品(超导转变温度Tc=91 K)在17 K下沿节点方向的ARPES原始图谱,通过对图4(a)做动量分布曲线(momentum distribution curve,MDC)拟合得到色散分布曲线(图4(b))和MDC半高宽(图4(b)右下角)。从中可以很明显的看到在70 meV处原始图谱和色散曲线有明显的“扭折”结构[24−29]。在同样的能量位置,MDC半高宽也有明显的下降。目前普遍认为此处扭折的出现是由于电子与某种玻色子相互作用引起的,但关于此玻色子具体是声子[28,29]还是磁振子[25,26,30]尚未明确。在动量范围很小的情况下忽略矩阵元效应,ARPES的强度谱图可以表示为:

其中谱函数A(k,ω)为:

式中 Σ′(k,ω) 为电子自能实部,Σ′′(k,ω) 为电子自能虚部,ϵk为裸带能量。由式中可以看出对于固定能量ω,谱函数A(k,ω)为洛伦兹线性,因此对MDC曲线可以用洛伦兹函数进行拟合[31],并从中提取出电子自能的实部和虚部。提取电子自能实部的时候需要用到裸带“ϵk”,在分析电子自能精细结构与其随温度变化的关系中,靠近费米能级附近小能量范围内可以选用近似线性裸带来提取电子自能的实部。如图4(b)中虚线所示,选用色散曲线中费米能级与−0.4 eV处两点所连成的直线作为经验裸带。这样,精细结构就会在电子的“有效自能”中出现峰值或者弯曲[32]。

图4.最佳掺杂 Bi2212样品在 T=17 K时沿节点方向 (Γ(0,0)− Y(π,π))的 ARPES 图谱。 (a)原始能量-动量谱图,右下角显示了布里渊区中的动量测量线;(b)通过对(a)做MDC拟合得到的色散关系,费米能级和−0.4 eV连结的直线(虚线)作为提取电子自能实部所需的裸带,右下角为相应的MDC半高宽[27]
选取128 K时色散关系的费米能级与−0.4 eV的连线为经验裸带提取电子“有效自能”的实部得到电子自能实部随温度变化的关系(图5(a))。得益于高分辨的 ARPES,从提取的电子自能中可以明显的发现数个精细结构特征(图中以黑色箭头标出),除了在70 meV附近处明显的精细结构,在节点区域附近很大的动量范围内都能观察到在∼115 meV和∼150 meV也存在着精细结构。同时在94 meV附近也有一个细微的精细结构,尤其是在靠近节点区域最近的两个动量测量线内更为明显。此外,在费米能级到 70 meV之间也观察到了精细结构存在的迹象,但这个特征十分的微弱,需要进一步的实验来确定。对于高能∼115 meV和∼150 meV处出现的结构,其能量尺度高于该材料中声子谱最高能量(90 meV)[33]和磁振子最高能量(42 meV)[34],因此不能简单地归功于电子与单个声子或磁振子模式的相互作用。尽管电子自能中,电子与低能模式的玻色子相互作用能够延伸到高能,但是这并不会在高能引起曲率的改变[35]。这可能对应着在高能区存在着新的电子耦合模式,具体起源还需要进一步的研究。
为了避免裸带选取的影响,从图5(a)中获得电子自能相对正常态(T=128 K)的温度变化关系(如图5(b))。随着温度的变化,在进入超导态时,电子自能发生剧烈的变化,伴随着∼70 meV处峰的锐化以及∼115 meV和∼150 meV处结构的出现。这种剧烈的变化意味着节点区域可能对高温超导的产生起着重要的作用。
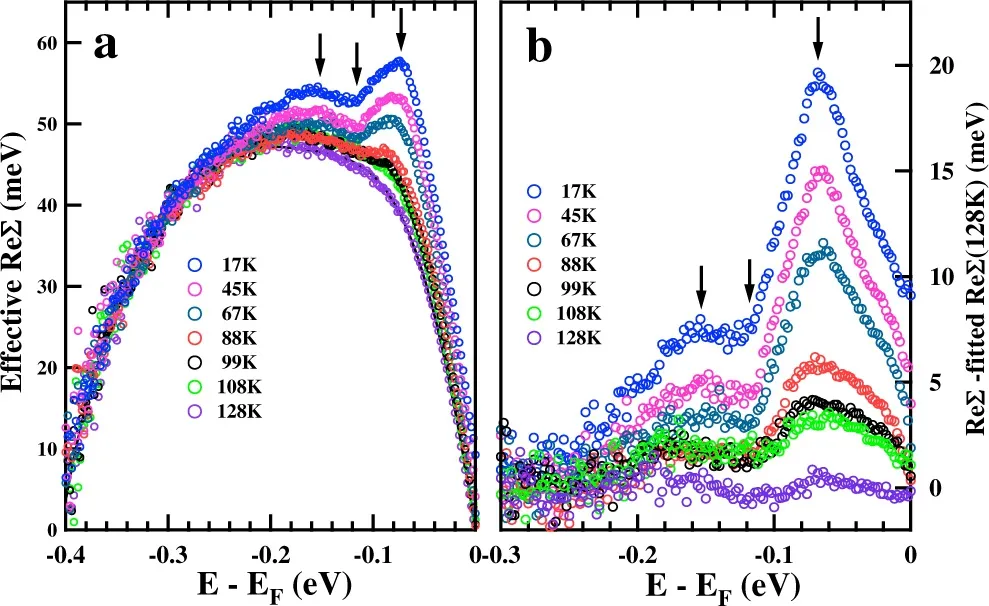
图5.(a)有效电子自能实部随温度的变化关系;(b)不同温度下有效电子自能与128 K的自能实部之差[27]
对于两处较高能量的精细结构的起源目前主要有以下几种猜测,但均无法完全解释。第一种解释是高能精细结构的出现是由于超导能隙的打开而使低能∼70 meV处的结构移至高能,如果最大超导能隙为∼35 meV则∼70 meV处的耦合结构将会移至∼105 meV处[36]。但是这样却无法解释更高能量∼150 meV处的结构,并且对于超导态下∼70 meV处结构仍然存在也无法说通。另一种解释是电子与多个玻色子发生了耦合,但是通常这种耦合所造成的效应会十分的微弱[37],而且这需要更多的研究去进一步地证明这样的过程是否能够产生一个随着温度降低而不断增强的高能特征。还有一个可能就是电子与其他高能元激发的耦合,其中比较可能的是中子散射中观察到的具有大能量范围(最高至200 meV)和强温度依赖关系的自旋涨落[38,39]。
总而言之,虽然目前对于节点区出现的这些精细结构的起源已经有了一些深入的研究和猜测,但仍没有形成共识。其具体的起源与机理、以及是否与高温超导电性相关仍需进一步的探索。
B.反节点区的研究
反节点区是指在布里渊区中 (π,0)附近的区域(图3中黑色圆圈区域)。在反节点区域中也存在由于电子–玻色子相互作用产生的扭折结构,但在反节点区域中扭折的许多特性与节点区域不同[25,29,30,40−49]。 图6为不同掺杂 Bi2212样品在不同温度下的反节点区ARPES原始谱图。在谱图中可以很明显的观察到两种不同的能带,一种为高结合能的成键带(记为B),另一种为低结合能的反键带(记为A),这两种能带在第一布里渊区中的位置在图6(f)中分别以红色和黑色标出。在正常态下B能带的色散关系为无结构的线性关系(图6(a)),但随着温度降到10 K样品进入超导态以后,在靠近费米能级附近色散曲线的谱重就发生了变化。除了因为超导能隙打开而造成的费米能级处谱重的损失外,在∼40 meV处发生了一处明显的扭折(图6(b))。同样的情况在过掺杂71 K和最佳掺杂91 K样品中也有出现(图6(c)和图6(d))。
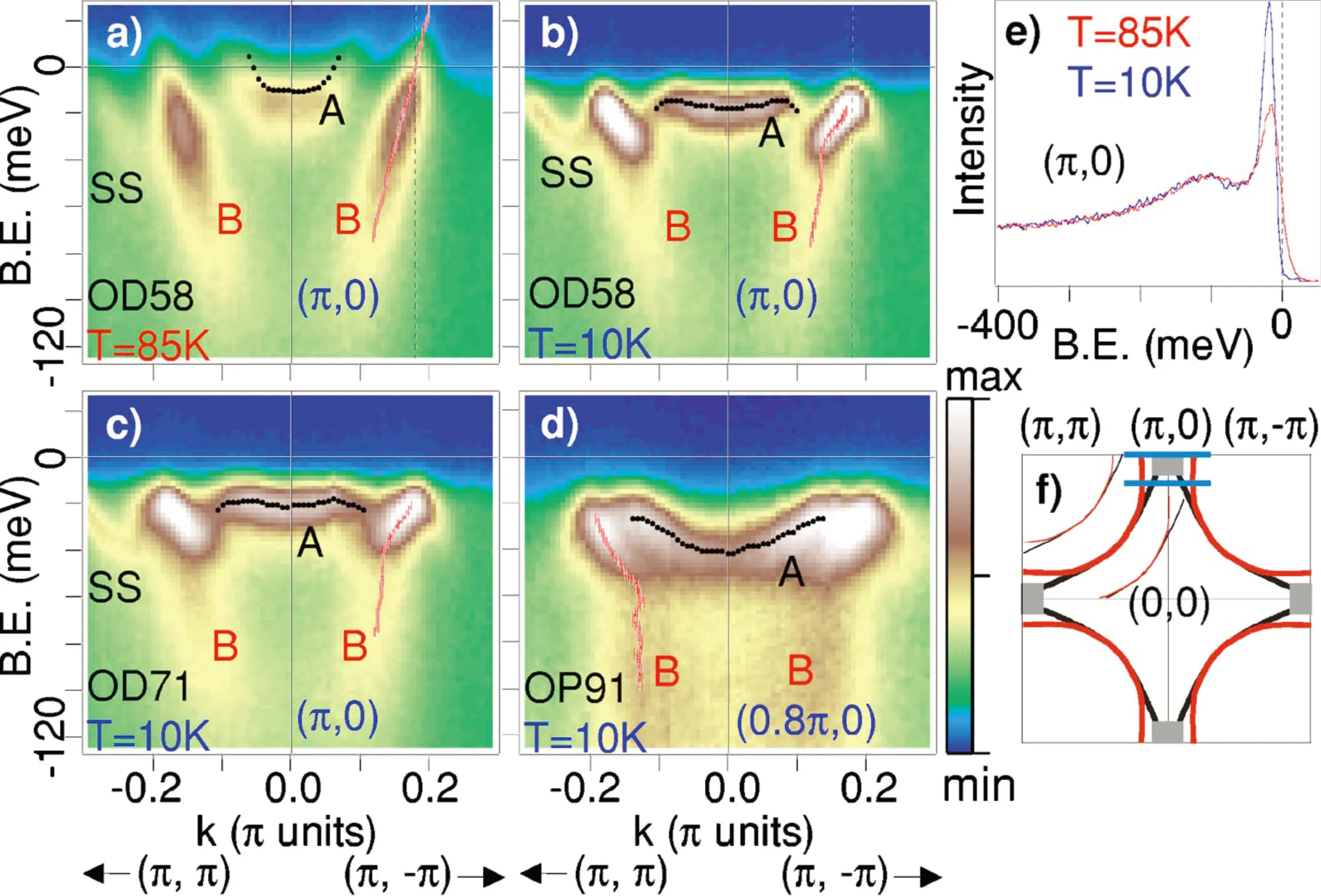
图6.反节点区域的ARPES色散谱图[45]
从图7(a)可以看出在正常态下电子自能的色散关系没有扭折结构。为了更清楚的发现温度依赖关系,图7(a)中的插图通过不同温度色散曲线减去正常态(85 K)时的色散曲线来近似提取电子自能实部(忽略正常态下其他因素导致的电子自能)。由于超导能隙的打开,在0∼25 meV处没有准粒子峰,只考虑在25 meV以上MDC拟合得到的结果。可以看到在正常态时几乎观察不到电子自能峰值的出现,而在进入超导态后电子自能的峰值开始出现且随着温度的降低而增加,且峰的位置基本维持在∼40 meV附近。图7(b)为利用计算得到的Bogoliubov准粒子色散关系提取的电子自能实部。图7(d)为在图7(a)中每个温度下提取的电子自能实部最大值,从中可以更明显的发现这个相互作用在进入超导态(T<71 K)时才开始出现,图7(d)中还标记了超导能隙随温度的变化关系与自能实部的变化表现出同样的趋势。虽然利用EDC分析方法观察到了正常态反节点区也存在∼40 meV结构的迹像[48],但是并没有得到广泛的证实。
对于反节点处扭折和节点处一样至今仍不清楚其具体机理。目前对反节点处的解释主要分为两种,一种是由于超导能隙打开而引起的产物,另一种是由于电子与声子、集体激发的磁振子或者其他玻色元激发的强耦合。但是这两种解释都无法完全解释这些奇异的现象,其起源还需要进一步的探索。
对节点与反节点区域的扭折做一个简单的比较,可以发现相比于节点处扭折,反节点处的扭折有更强的温度依赖关系并且在超导转变温度以上时扭折消失,而节点处的扭折在转变温度以上非常明显;此外两者所对应的能量尺度也大不相同:反节点处为∼40 meV而节点处为∼70 meV。
C.相互作用的动量依赖关系
为了更好的理解节点处与反节点处扭折之间的关系与区别,理解节点区的 70 meV扭折是如何演变为反节点 40 meV处的扭折需要探测其动量依赖关系[50−52],这将有助于理解高温超导机制。超高能量分辨率的激光角分辨光电子能谱为此类研究提供了契机。
通过超高分辨率ARPES获得的色散能够观察到在反节点区低能处存在着两个明显扭折结构,提取的电子自能实部也在∼40 meV和∼78 meV处出现了峰值(如图8(d))。同时,在靠近节点区提取的电子自能实部中也能观察到两个峰值。在后文中,对反节点区稍低能量∼40 meV处扭折记为低能扭折,稍高能量处扭折记为高能扭折。为了更好的探究这两种模式,尤其是扭折强度更强的低能处激发模式,对过掺杂Bi2212样品在超导态(17 K)下从节点到反节点区域选取了五个不同的动量测量线进行测量,得到的ARPES原始图谱如图8(a1)–(a5)所示。对原始图谱进行能量分布曲线(energy distribution curve,EDC)二次微分处理得到更能体现强度变化的谱图(图8(b1)–(b5)),可以看到除了节点处由于高能扭折与低能扭折几乎重合而显得无法分辨以外,其余四个动量测量范围内均出现了两个共存的扭折结构,EDC拟合曲线也出现了两处低谷(图8(c))。提取不同动量下的电子自能有效实部曲线如图8(d)所示,两处扭折的能量尺度表现出了截然不同的动量依赖关系。可以明显的看到高能处扭折能量尺度随动量的变化保持在∼78 meV几乎不发生改变,低能处扭折能量随着远离节点从∼70 meV逐渐变为∼40 meV。
此外高能扭折与低能扭折对温度也体现出了不同的依赖关系,探测过掺杂82 K样品在靠近反节点区域、节点区域以及反节点区至节点区之间三个动量范围内不同温度下不同动量处的电子结构(图9)。可以发现对于靠近反节点区域,超导诱导的电子自能转变主要局限在低能量尺度的结构;对于节点与反节点之间的动量范围,两个能量尺度的结构均能清晰的看到且低能结构耦合强度相比于反节点区更弱;对于节点区域,超导诱导的电子自能改变量很大并且在正常态下高能扭折仍然存在,但是在节点区两处扭折能量尺寸十分接近很难进行分辨。图9中(g)和(h)在正常态(90 K)下仍能观察到自能的改变,因此高能处扭折的形成很有可能是由于电子与∼70 meV处的声子相互作用形成的。
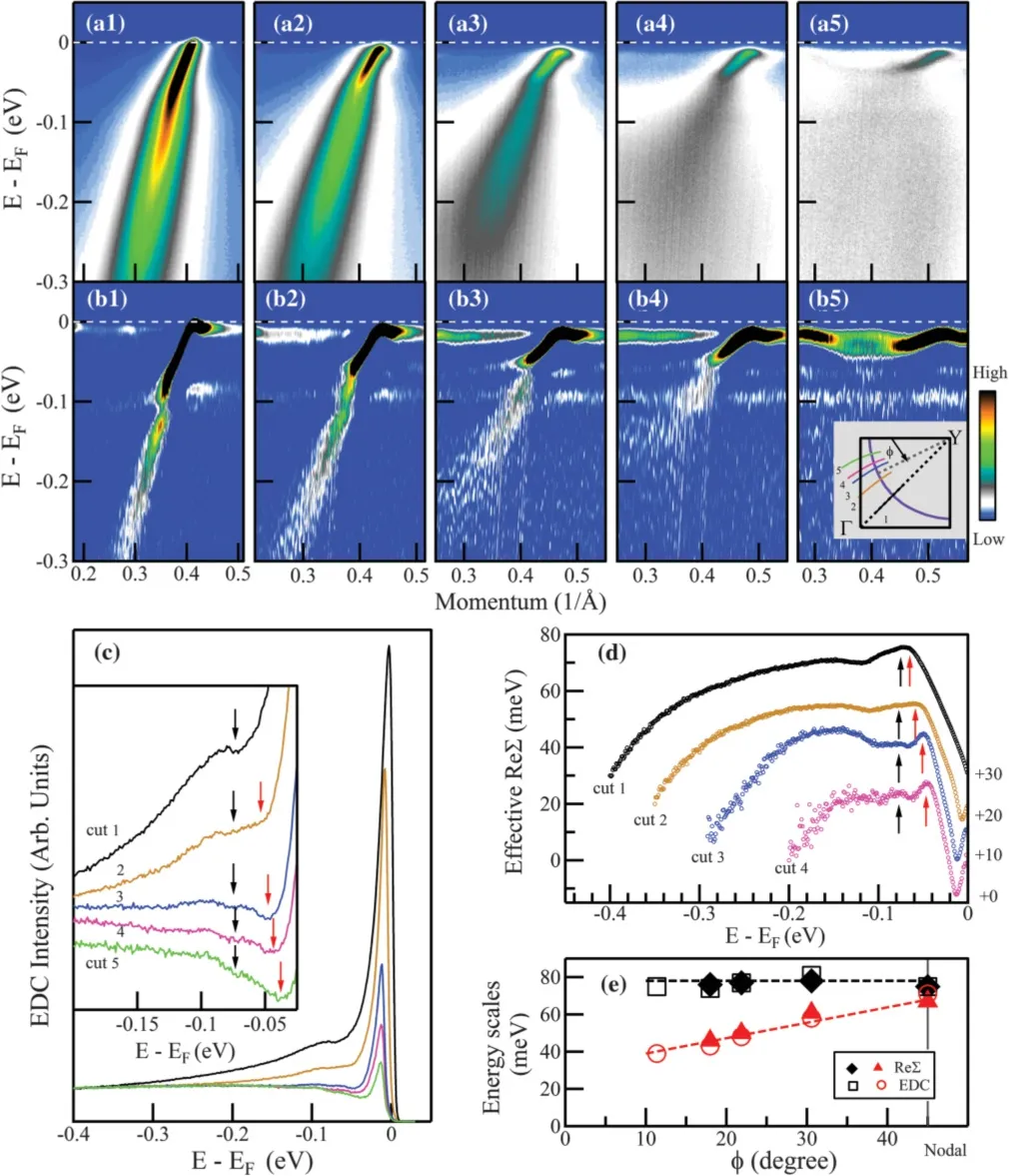
图8.扭折的动量依赖关系。(a1)–(a5)过掺杂 82 K样品在 17 K 下的 ARPES原始图谱;(b1)–(b5)为对应 (a)图中的EDC二次微分曲线,内部插图为对应的第一布里渊区中的动量测量线;(c)五个动量下的费米动量处的 EDC曲线;(d)提取的电子自能有效实部;(e)两处扭折能量尺寸的动量依赖关系[53]
由此可以看出,前文叙述的节点区域∼70 meV处的扭折其实为两处能量结构共同造成的。但无论是高能处的扭折结构还是低能处的扭折结构均不能用传统图像中的电子–玻色子耦合模式来解释。因为在传统的耦合模型下,如果电子–玻色子在正常态下的耦合能量为Ω,则在进入超导态后由于超导能隙的打开耦合能量会移到Ω+∆0(对于各向异性的超导能隙∆0为最大超导能隙[36])。但是观测到的高能扭折在正常态时为∼78 meV,按照先前传统的理论在进入超导态后耦合能量应该移至105 meV[36](对于过掺杂 81 K样品最大超导能隙为25 meV),但实际观测到在进入超导态后耦合能量仍是在∼78 meV处保持不变。即使考虑电子散射只局域在一个很小范围内的向前散射理论[55],从节点到反节点区域耦合模式的能量平移为局域的超导能隙(从0增加到最大超导能隙)[56],这样虽然解释了在节点处扭折能量在进入超导态不发生移动,但仍不能解释进入超导态后高能扭折能量在一个大动量范围内保持不变。对于低能模式的耦合则更加难以进行解释,低能耦合的能量尺度从节点到反节点从∼70 meV减小到∼40 meV与向前散射理论模型背道而驰。可见铜氧化物高温超导体的电子–玻色子耦合不能由传统超导体的理论进行简单的应用来解释,其内部的物理机理还需要进一步的研究。
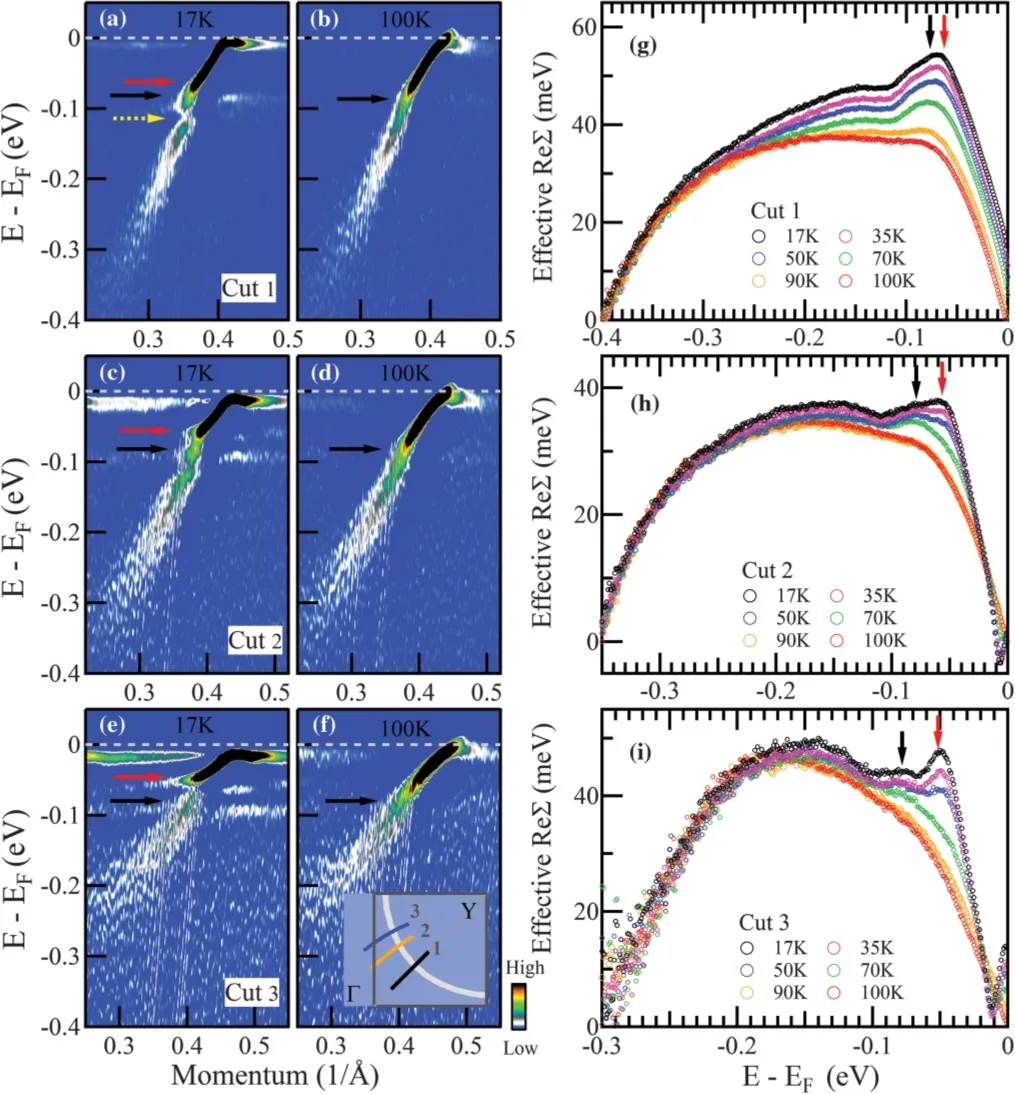
图9.温度依赖关系。(a)、(c)、(e)为三处动量测量线下超导态 (17 K)的二次微分图谱;(b)、(d)、(f)为对三处测量线下正常态 (100 K)的二次微分图谱;(g)、(h)、(i)为三处测量线下提取的电子自能有效实部[53]
D.配对电子自能的提取
和传统超导体类似,在铜氧化物超导体中已经被证实相反自旋和动量的电子互相配对形成自旋单态[57],其内部的超导能隙也已经被证明与传统超导体的s波对称性不同,而是具有 d波对称性[58]。但是铜氧化物超导体中电子配对的起源目前还处于争论之中。在传统超导体中,用BCS理论得到了很好的解释,即电子以交换声子的方式来形成库珀对[59]。但是在铜氧化物超导体中,电子之间是否能够自发的形成配对还是如传统超导体一般需要一个集体激发的纽带来促成配对还不得而知[60]。在传统超导体中提取出的电子正常态自能 Σ(ω)和电子对的自能ϕ(ω)为证明声子就是电子配对的纽带提供了强有力的证据[61,62]。因此在铜氧化物高温超导体中,进行电子配对自能的提取对理解其形成机理具有重要意义。传统的提取电子配对自能是从隧道谱和光学测量数据中提取的,但这两种实验手段是对整个动量范围进行积分不具备动量分辨功能,而铜氧化物超导体由于强烈的各向异性具有明显的动量依赖关系,因此从传统的隧道谱和光学实验提取铜氧化物电子自能非常困难[63−68]。而ARPES因为具有独特的动量分辨功能,成为了研究铜氧化物自能最有效的研究手段。

图10.欠掺杂89 K Bi2212样品中超导态下的Bogoliubov准粒子色散。(a)考虑超导能隙∆=10 meV、线宽Γ=5 meV下模拟的单粒子谱函数A(k,ω);(b)20 K下模拟的单粒子谱函数乘上费米分布函数f(ω);(c)70 K下模拟的单粒子谱函数乘上费米分布函数 f(ω);(d)模拟对应的布里渊区中动量范围;(e1)–(e5)欠掺杂 89 K Bi2212样品中不同温度下靠近反节点区ARPES采集到的原始图谱;(f1)–(f5)原始ARPES图谱除去费米分布函数后得到的图谱[54]
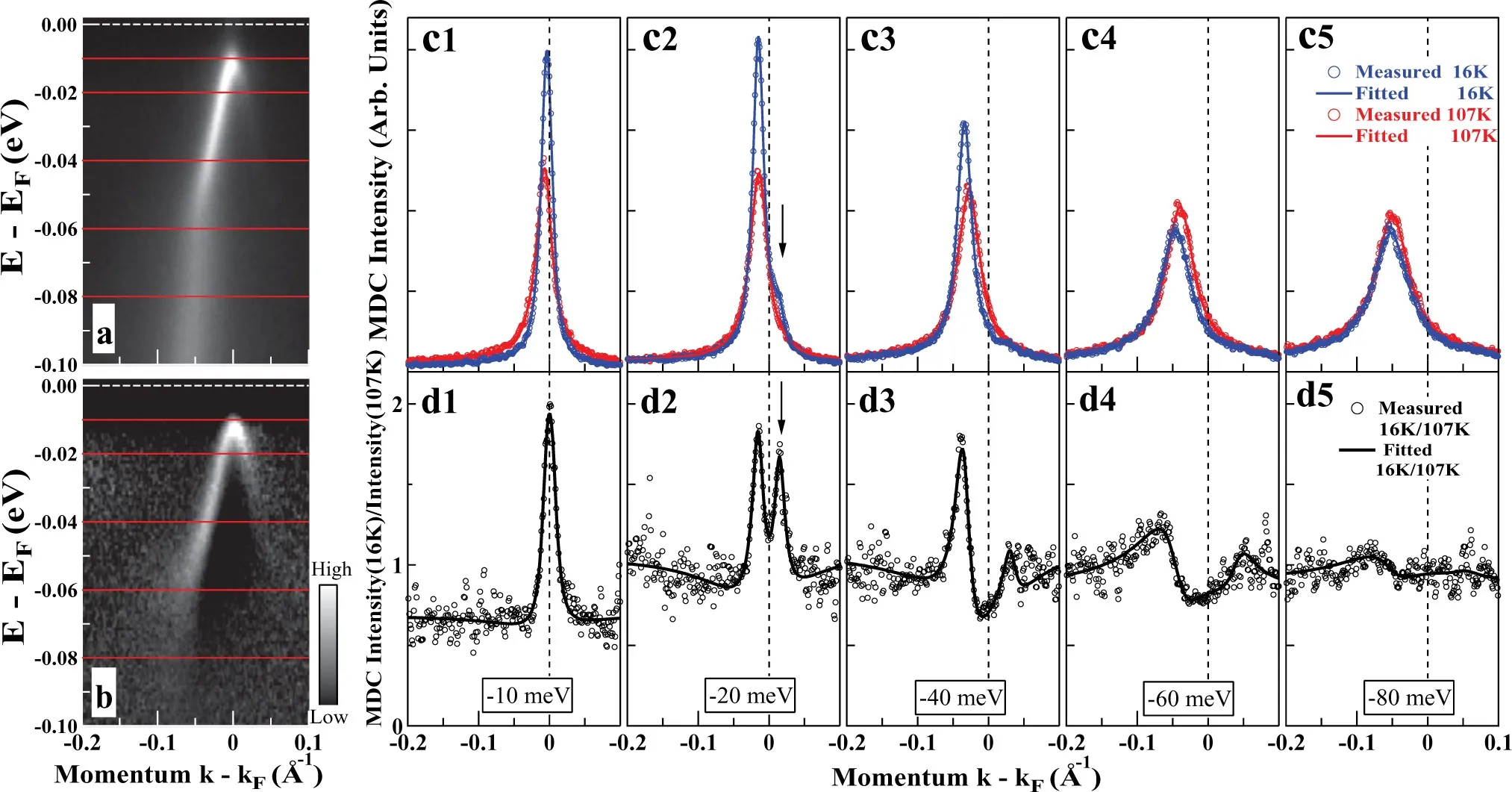
图11.在超导态Bi2212样品中Bogoliubov准粒子色散靠近费米能级处出现能带向下弯折。(a)16 K下沿着图10(d)中方向测得的ARPES谱图,与图10(e1)仅色调不同;(b)同个测量方向上超导态16 K的原始图谱除以正常态107 K的原始图谱;(c1)–(c5)对(a)中红线对应的能量处正常态和超导态的MDC曲线 (d1)–(d5)16 K图谱除以107 K图谱后不同结合能下拟合得到的MDC曲线[54]
根据BCS理论,在超导体中低能激发为Bogoliubov准粒子表象中相干的电子、空穴混合。在靠近费米动量时,BCS谱函数可以近似写为:
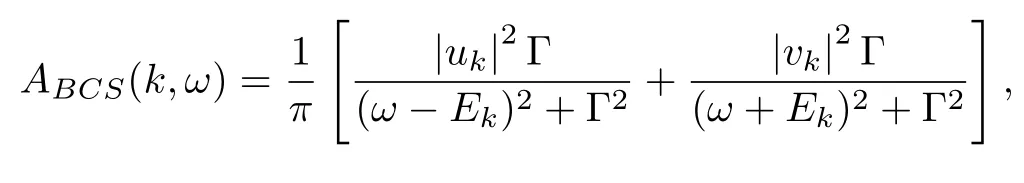
其中uk和vk是相干因子,Γ为线宽常数,且Ek=(其中ϵk为正常态的能带即裸带),∆(k)为能隙函数。图10(a)模拟了在∆=10 meV时在70 K下靠近反节点区的谱函数A(k,ω),可以很明显观察到有两支Bogoliubov准粒子色散分布在费米能级 (Ef)两侧,两者之间存在着超导能隙2|∆|且满足关系式A(k,ω)=A(−k,−ω);此外每个分支在靠近费米动量处都有一个反向的弯折,对应的MDC曲线上显现出两个峰值(图11(c))。ARPES测量得到的谱图强度还会受到到费米分布和矩阵元效应的影响(式(1))并且费米能级以上几乎没有信号只有一定的热力学展宽(图10(b))。图10(e1)–(e5)为不同温度下对欠掺杂89 K Bi2212样品ARPES采集的原始图谱。在16 K下,由于费米分布函数的影响,费米能级以上几乎无电子占据(图10(e1));而在相对高温但仍在超导态的 70 K(图10(e2)) 和 80 K(图10(e3))中仍能看到费米能级以上的一些特点。通过除去费米分布函数的影响,可以看到费米能级以上的Bogoliubov准粒子色散(图10(f2)、图10(f3)),并且两支能带关于费米能级处的费米动量成中心对称关系。而在温度高于超导转变温度以上,能带恢复成为正常态能带,没有能隙的打开(图10(e4)、图10(e5))。最重要的是在低温下靠近费米能级处能带出现了弯折[69](图10(e1))。如果能带确实出现弯折,则在能隙以下的MDC曲线中会出现两个峰:一个为由主带产生的峰值,另一个为由弯折的能带产生的较弱的峰值。对16 K和107 K下的ARPES图谱在−10 meV、−20 meV、−40 meV、−60 meV 和−80 meV处分别进行 MDC拟合(图11(c1)–(c5)),在−20 meV的MDC曲线中能看到第二个峰值的存在(图11(c2)中的黑色箭头)。为了更明显地观察到弯折的现象,图11(b)将超导态16 K下的ARPES原始谱图除以正常态下 107 K的 ARPES原始谱图,并对其作 MDC拟合得到图11(d1)–(d5),从 (d2)中可以更明显地观察到双峰结构。
能带弯折的出现与对称的Bogoliubov色散说明了在 Bi2212中,Bogoliubov准粒子色散表现出与BCS公式一致的形式。在大动量范围内的MDC中出现了双峰结构更是提供了用Eliashberg形式代替BCS近似来直接提取正常电子和配对电子的自能。在ARPES中,测得的单粒子谱函数正比于单粒子格林函数的虚部:
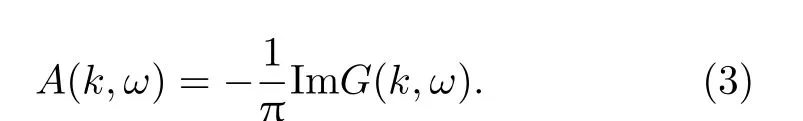
考虑超导态下圆柱型费米面,格林函数可以写为:

其中Z(ω) 为重整化参数,ϕ(θ,ω)=ϕ(ω)cos(2θ) 为配对电子自能,其能隙函数 ∆(ω)的关系为 ∆(ω)=ϕ(ω)/Z(ω)。需要注意的是只有当动量测量线指向 (π,π)点、并且费米面近似为圆形时此公式才成立。图10(d)所示的动量测量线均基本符合这个要求。在正常态时只需令式(4)中ϕ(ω)=0即可。

图12.超导态下的Bi2212样品在ARPES测量中提取的正常态和配对电子自能的实部和虚部。(a)三个典型动量下的正常电子自能实部;(b)三个典型动量下的正常电子自能虚部;(c)三个典型动量下的配对电子自能实部;(d)三个典型动量下的配对电子自能虚部[54]
图12显示了在三个典型动量下提取出的正常态电子自能的实部和虚部 Σ′(ω) 和 Σ′′(ω),以及配对电子自能的实部和虚部ϕ1(ω)和ϕ2(ω)。配对电子自能可以直接通过式 (3)和式 (4)拟合得到,而正常电子自能则需通过 Σ(ω)=[1−Z(ω)]ω得到。从图12中可以看到提取出的自能有轻微的动量依赖关系,且四个形式的自能为互相独立的变量,互相之间没什么明显的联系。在图12的自能中,低于∼20 meV的结构可以认为是超导能隙打开引起的(对于布里渊区中 cut3、cut4、cut5超导能隙分别为 10、12.5、15 meV)。而对于更高能量,有两处明显的特点,一处为电子正常态自能实部∼54 meV处的峰包,这对应着前面所说的扭折结构;另一处为正常电子自能虚部和配对电子自能虚部在∼40 meV处出现的低谷。同时也注意到配对电子自能在高结合能(∼50 meV)以上表现为和正常态一样的无结构背底。
总而言之,在铜氧化物超导体中,电子配对是否需要纽带还无法下定论。如果配对的纽带真的存在,它应该会和传统超导体中一样在正常电子自能和配对电子自能中同时显现出来。目前声子、磁振子以及自旋涨落是三种被认为最可能的配对纽带,但是目前所获得的玻色谱函数和正常电子自能与配对电子自能之间没有明显对应关系。并且在传统图像中,正常态下与能量为Ω的模式耦合在进入超导态后会移动到Ω+∆(2∆为最大超导能隙[36])的现象也没有被观察到。此外,各向异性的超导能隙和电子结构以及反常的正常态(比如赝能隙的出现)也可能导致玻色谱函数与正常电子自能和配对电子自能之间的关系变得更为复杂。其中的关系与机理还需要着更多的理论和实验研究。
III.时间分辨角分辨光电子能谱对多体相互作用的研究
利用超短脉冲激光来研究电子–声子相互作用的动力学是一个新兴的领域[70,71]。但是仅用纯光学的时间分辨技术无法直接探测产生的准粒子或得到材料内部关于动量的信息,从而只能间接的获得电子自能、非平衡态的多体相互作用等有可能揭示固体微观性质的参数。而近年兴起的时间分辨角分辨光电子能谱技术将两者特点很好地结合起来,能够直接探测材料内部电子结构的动力学过程。这一独特的优势也让trARPES成为了研究多体相互作用的重要技术手段。目前trARPES在高温超导体光诱导的准粒子重组动力学[72−76]和能隙动力学等方向上有了初步的研究[77−90]。
A.节点区的研究
节点区电子态是否与高温超导存在关联一直存在争议。TrARPES可以同时探测节点区电子态与远离节点区超导能隙在激光泵浦作用下的超快演变。这为研究超导能隙与节点区的多体相互作用是否存在关联提供了一种新的思路。
图13(a)中可以看出在泵浦通量为 24µJcm−2下,平衡态的谱图存在之前提到的在70 meV处明显的重整化扭折。通过泵浦,调节泵浦激光和探测激光的时间间隔为1 ps时,从扭折能量处到费米能级出现了一个明显的谱重损失[73],直到时间间隔为 10 ps时才从瞬时图谱重新恢复到平衡态。图13(b)为对图13(a)进行MDC拟合得到的色散关系曲线,从图13(b)中可以观察到泵浦造成的变化主要在扭折能量附近,在靠近费米能级处以及高结合能处几乎没有任何变化。

图13.接近最佳掺杂Bi2212样品的时间分辨谱图。(a).平衡态 (t=−1 ps)和泵浦后的瞬时态(t=1和10 ps)的谱图;(b).从(a)中MDC拟合得到的色散关系曲线四幅插图分别为不同结合能处 (−0.15,−0.07,−0.02 eV)的局部放大以及在布里渊区中的动量测量线[81]
通过提取瞬时态和平衡态的电子自能(图14),可以清楚地观察到前文提到的在平衡态电子自能中的两处电子自能精细结构(图中以黑色箭头标记处),其中以∼70 meV扭折处最为明显。对比泵浦前后的电子自能可以很明显的发现电子自能的实部在扭折能量附近(40至 90 meV)受到极大的抑制,并且这个抑制的效果随着泵浦通量的增加而增强直至将其精细结构完全抑制时达到饱和。这种泵浦效应不应是由于泵浦导致温度升高而产生的,相比于温度对电子自能在整个能量范围内均会产生影响,泵浦导致的电子自能改变只局限在扭折附近很小的能量范围内。这意味着光学泵浦产生了除升温以外的其他未知效应。
此外,泵浦诱导的电子自能虚部变化(图14(b))局限在扭折能量和费米能级之间,并随着泵浦通量的增加而增加,这和电子自能实部的变化基本保持一致。图14(b)中的插图为热效应对电子自能虚部的影响,相比于泵浦导致的变化只局限在很小的能量范围内,热效应会在整个能量范围内造成电子虚部的变化。图14(c)为正常态下泵浦对电子自能实部和虚部的影响,即使在24µJcm−2的泵浦通量下,泵浦对电子自能实部和虚部的改变几乎可以忽略不计。

图14.节点处平衡态和瞬时态的电子自能。(a)在超导态(17 K)时不同时间延迟以及不同泵浦通量下的电子自能实部;(b)不同泵浦通量下拟合MDC曲线的半高宽(电子自能虚部)随结合能变化曲线,插图为正常态以及超导态时黑色箭头附近能量范围内电子自能虚部;(c)正常态下(100 K)电子自能实部和虚部在临界通量(13µJcm−2)下随结合能变化关系[81]
另一个重要的现象是泵浦会抑制超导能隙,这个抑制作用随着泵浦通量的增加而增强,直至超导能隙完全闭合(图15(b)),这与之前电子自能的泵浦通量依赖关系相似。将相同时间下超导能隙的减小(图15(b))与电子自能实部的改变量(图15(a))进行比较(图15(c)),发现它们几乎成线性关系。图15(d)则显示了电子自能的恢复速率与节点处的耦合强度在低通量下与泵浦通量呈良好的线性关系,这与非平衡态准粒子 bimolecular recombination model类似[76,82],但随着泵浦通量的增加达到临界值后恢复速率不再增大而出现“瓶颈效应”。图15(e)为泵浦引起的非平衡态最小能隙和最大电子自能实部改变量以及电子–玻色子耦合强度λ随泵浦通量的变化,其中耦合强度和变化前后的费米速度的关系为λ′≡λ+1=vF/v0[83]。可以看出电子–玻色子相互作用随着泵浦通量的增加而不断变弱,当超导能隙被完全抑制时达到最小。这种现象无法通过泵浦激光致使样品升温解释,因为热力学展宽导致扭折处的拖尾效应会随着温度的升高一直增加而不会达到饱和[27]。此外,在和Bi2212具有相似晶体结构和电子结构的金属态Bi2201中(Tc<5 K),观察到泵浦对Bi2201电子自能的影响几乎可以忽略不计。以上的这些现象均不能用泵浦导致样品瞬间加热升温来解释,此外这些现象在正常态和金属中均不适用,意味着这些现象很可能源于泵浦超导体所展现出的本征特性。
上述现象意味着电子自能的重整化对高温超导配对能隙很可能有促进作用。对于这些现象是否由电子耦合常数的变化或是光诱导电荷的退局域化导致的Jahn-Teller效应的减弱与电声相互作用的软化引起的[84,85]还需进一步的研究。
B.动量依赖关系
和高分辨ARPES一样,考虑节点与反节点区物理机理的不同,研究trAPRES对多体相互作用动力学的动量依赖关系将有助于理解其内部机理的演变。之前的高分辨ARPES的介绍展现了铜氧化物超导体中出现的peak-dip-hump(PDH)结构,此处将对PDH结构在trARPES下的演变以及动量依赖关系进行细致的介绍。
PDH结构可以视为电子色散扭折的一部分,是玻色子辐射衰变路径引起的准粒子寿命的突然下降。一个具有长寿命的准粒子在强度谱中应该是一个尖锐的峰,而一个短寿命的准粒子则是一个宽广的波包。PDH结构的出现表明在ARPES能量分布中同时观察到峰和波包。
在前面已经介绍过泵浦脉冲会在皮秒尺度上短暂地抑制超导性质并留下一个瞬时的赝能隙态;这里具体讨论泵浦对PDH结构的影响及其动量依赖关系。图16(a)和(b)分别为过掺杂 70 K Bi2212样品在超导态20 K下泵浦前(t<0 ps)和泵浦后(t>0.9 ps)的 ARPES原始谱图,泵浦通量为 24µJcm−2。对比泵浦前后的谱图可以发现扭折被明显地抑制。测量的动量在第一布里渊区内的范围显示在图16(a)的插图中,在此动量下超导能隙与赝能隙均存在。对于泵浦后的图谱,通过上一节的介绍已经知道在此通量下超导电性已被完全抑制,但仍可以发现能隙的存在,这是因为瞬时的赝能隙态[80,87]。

图15.泵浦诱导改变动力学。(a)不同泵浦通量下泵浦对节点处电子自能实部改变量随不同延迟时间变化的关系(为了区分在竖轴方向做了平移);(b)在离节点附近(测量线在布里渊区位置见图中插图)不同泵浦通量对超导能隙的抑制量随不同延迟时间的变化关系(改变量以最大能隙处为依据归一化);(c)不同泵浦通量下每个时间延迟泵浦诱导的自能实部改变量与能隙改变量的关系;(d)节点处自能改变恢复速度与费米速度恢复速度;(e)泵浦诱导的非平衡态最小能隙和最大电子自能实部改变量随泵浦通量的变化[81]
图16(c)为对泵浦前后整个动量测量范围内的强度积分归一化后的曲线,图中可以很明显的看出平衡态的强度曲线中有着明显的PDH结构,但是在泵浦后 0.9 ps,PDH结构中的峰值和谷值都被明显地抑制。图16(c)内部的插图具体地显示了这个抑制的现象。图16(d)和(e)更明显地对比了泵浦前后谱图强度的变化,图16(d)为泵浦前后谱图强度的差,图16(e)为对图16(d)在整个动量范围内的积分曲线。可以看出在费米能级附近的区域(蓝色区域)由于超导能隙的填充和部分非占据准粒子态被占据而造成强度的增加。而在30 meV附近(红色区域)强度的减少则是由于PDH结构中峰值受泵浦的抑制以及部分准粒子占据态的减少造成。但是在靠近70 meV区域的强度增加却无法用电子占据态的改变来解释,这很可能是由于态密度自身的改变引起的。图16(f)则显示了随延迟时间变化的动量积分强度变化,可以看见强度的改变在泵浦后很快出现,并在数皮秒后仍然存在。
为了更好地理解泵浦对PDH结构的影响,不同动量与掺杂下的测量结果如图17所示。(a)和(b)分别为欠掺杂78 K Bi2212样品和过掺杂70 K Bi2212样品在20 K时不同动量测量线下的−∆I曲线。为了更方便地比较,所有曲线均以100 meV为单位1作处理。对70 meV处谷值改变的最大处记为∆Idip,将每条曲线的∆Idip标记在图17(c)中。
在欠掺杂样品中,节点区的低谷并不能明显地观察到,但除了节点区以外 ∆Idip在过掺杂和欠掺杂样品中极为相似。这证明此处低谷和赝能隙可能没有联系,因为赝能隙在过掺杂样品中远小于欠掺杂样品[88],同时也说明不是由于 Bi层劈裂引起的[89−92],因为 Bi层劈裂只会在反节点区产生 PDH结构。此外,还能观察到 ∆Idip随着ϕ的增大而增大,这和之前观测到的PDH结构在靠近反节点区更强吻合,PDH结构的动量依赖关系取决于电子–玻色子耦合强度的大小。另外,在140 meV处也出现了一个和70 meV处相似的极小值,这说明在140 meV处也存在着一个额外的低谷结构,这可能对应着前文高分辨ARPES中观察到的∼140 meV处谷结构。

图16.(a)过掺杂 70 K Bi2212样品在 20 K下平衡态的ARPES图谱;(b)同样样品在24µJcm−2泵浦通量下0.9 ps后的APRES图谱;(c)、(a)和(b)在整个动量范围内的强度积分曲线,内部插图为黑色箭头处的放大;(d)、(a)和(b)的强度改变量;(e)改变量在整个动量范围内的积分曲线;(f)动量积分的改变量和时间延迟的关系[86]。
定义pi为∫∆Idk在费米能级以下第i个最大或最小值处的能量。图18显示了每个pi的能量尺寸随动量变化的关系。p1表示PDH结构中由于在超导能隙边界一系列准粒子态堆积形成的峰。在节点区由于没有超导能隙,p1代表着电子温度的增加。当逐渐远离节点时,p1对应的能量不断变高,最后截止在超导能隙尺度∆eq。p2表示PDH结构中的低谷位置接近能带的扭折能量,p2在图18(c)中节点处为∼60 meV远离节点处为∼80 meV,但通过模拟发现p2并不能准确表示扭折处的能量。p3和p4的能量尺寸与∼140 meV处的结构相关。对于这处神秘的∼140 meV结构目前有两种较为认可的推测:一是电子和其他高能玻色子耦合形成即p4的位置为∆+Ω′,二是第一处电子–玻色子耦合的二阶影响即p4出现在∆+2Ω。
对于单动量测量和动量积分测量的PDH结构有着不同的解释。此处使用Nambu-Gorkov公式,将格林函数G和自能Σ看作2×2的矩阵,反对角元素表示电子对。通过Dyson公式,格林函数可以写为:
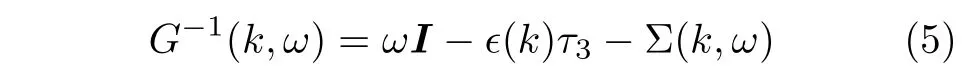
其中τ3为泡利矩阵,自能的正则形式为:

其中Z,ϕ,和χ为复数,通过相位的选择可以忽略,当ϵ(k)的斜率为常数的时候χ可以忽略。这时ARPES强度为:

其中G11为G中左上角的元素。采用两个近似,首先假设积分范围足够大能够覆盖色散曲线中绝大部分的强度,其次假设Σ,I0以及电子速度在积分范围内不依赖于动量,这样就可以得到动量积分强度为:
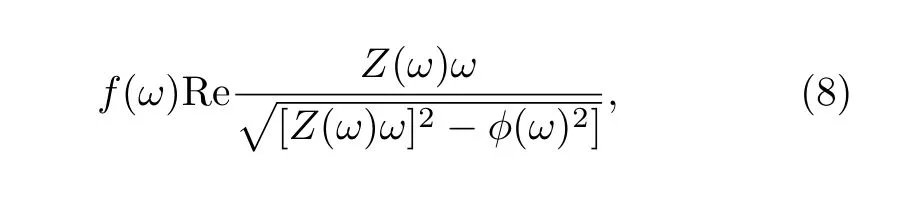
式(8)表明了只有当ϕ不为0且Z和ϕ有一定的能量依赖关系时才能产生PDH结构,也就是说必须要有超导能隙的存在和扭折的出现。在平衡态中这两个条件均得到了满足,而在泵浦后超导能隙被部分或完全地抑制,所以PDH结构也被部分或完全地抑制。
模拟的结果如图19,在模拟中通过Eliashberg公式用Z(ω)和ϕ(ω)来自洽计算。平衡态的模拟均假设T=20 K、能隙为30 meV,而在瞬时态的模拟中使用T=80 K和ϕ=0,耦合的玻色子能量为 35 meV。此外考虑超导能隙的大小不随动量变化,也就是说电子–玻色子散射只局限在反节点区。用电子–玻色子耦合常数来计算Z和ϕ,并将电子–玻色子耦合常数分为各向同性的分量λZ=1和具有d波对称性的分量λϕ[36]。 在λϕ取 0.2,0.1和 0.05时,平衡态下ϕ的实部和虚部分别如图19(a)和(b)所示。图19(c)为模拟的在λϕ=0.1时平衡态ARPES强度谱图,图19(d)则为模拟的从平衡态到瞬时态的强度改变量,可以看出这与实验观测的图16十分相近。图19(e)显示的为平衡态和瞬时态下动量积分的强度曲线,在平衡态的曲线中,PDH结构与实验观测十分相似,而在瞬时态时,由于超导能隙的抑制PDH结构消失不见。两者的差别具体显现在图19(f)中,这与实验观测到的图17也十分相似。此外可以看出p2的位置在80 meV处大于扭折能量∆+Ω=65 meV,可见p2并不能完全代表扭折处的能量。
最重要的一个发现是当λϕ增大的时候,低谷的强度变小。通过实验观测的结果对比模拟结果可以估算出λϕ的大小,这也许能够成为电子–玻色子扭折对d波高温超导体贡献的一个重要参数。实际上已经证明ARPES实验能够得到玻色子对超导电性的贡献程度[93],但是通过谷值强度的方法进行判断显得更加的简便。由于在模拟的过程中将能隙的尺寸视为定值、在式(8)中假设了积分范围足够大且忽略了电子–电子相互作用自能的影响,因此还需要更多的计算测试来改进此方法。或许这将确定电子–玻色子耦合与高温超导之间是否存在联系。

图17.(a)不同动量测量线下的欠掺杂78 K Bi2212样品动量积分的改变量;(b)在不同动量测量线下的过掺杂70 K Bi2212样品动量积分的改变量;(c)∆Idip随动量变化关系[86]。

图18.(a)pi所代表的具体含义;(b)欠掺杂Bi2212样品中各个pi能量尺度的动量依赖关系;(c)过掺杂Bi2212样品中各个p4能量尺度的动量依赖关系[86]
C.玻色子的受激辐射
玻色子的受激辐射在近代科技中有着重要的应用,它是激光的基本工作原理。在激光的产生中,入射的光子增加了激发态原子跃迁到更低能态的概率并产生一个相同能量的光子。有理论认为,类似激光中的受激辐射原理,超导体中被散射的库珀对在受激辐射的作用下会增大恢复到凝聚基态的概率,从而形成超导电流,但是这从实验上还未被证实过。超导体中可能存在的受激辐射过程必然涉及到复杂的多体相互作用,研究超导体中的受激辐射过程,将有助于人们理解其中的复杂多体相互作用。
前面介绍了在皮秒尺度上非平衡态准粒子的重组动力学,但是对于受激辐射往往是存在于更快的飞秒尺度上的动力学现象,因而在皮秒尺度的研究中往往被忽略。这里介绍利用trARPES在飞秒尺度上对铜氧化物超导体非平衡电子态的研究。
图20显示了超导态和正常态下欠掺杂 78 K Bi2212样品在节点处非平衡态准粒子的积聚。图20(a)为在泵浦通量为 2.4µJcm−2下的ARPES原始图谱以及不同时间延迟下泵浦导致的强度变化量。和前文所述一致,费米能级以下的强度减少,费米能级以上的强度增加,这意味着非平衡态准粒子的激发。此外,在0.9 ps时谱图变化的强度要大于0 ps时,这意味着需要一定的时间来积聚以达到非平衡态准粒子的最大数目。图20(b)中对整个动量范围内的强度积分曲线更明显地显示了这一特点。
定义费米能级以上非平衡准粒子的改变量为:
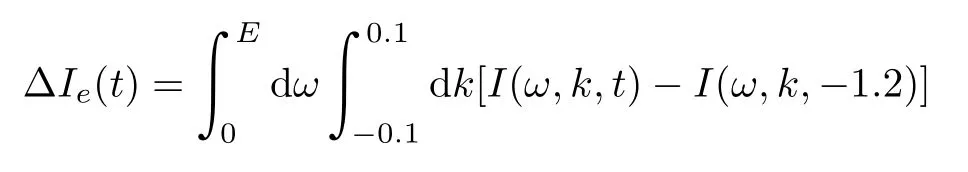
图20(c)显示在超导态 (20 K)和正常态 (90 K)下的 ∆Ie(t)。 可以看出最大强度改变量在 0 ps之后,这与图20(a)一致,将达到最大改变量所需的时间记为tbuildup。可以看出正常态下对于t>tbuildup时非平衡态准粒子数的衰减速率比超导态时更快,这和前面所述的保持一致。考虑更小的时间尺度,可以看出超导态达到最大强度改变量(tbuildup)需要1 ps左右的时间,而正常态下几乎瞬间就达到了最大改变量。同时注意到在最大超导能隙以上,非平衡态准粒子数也几乎立刻达到了最大值。
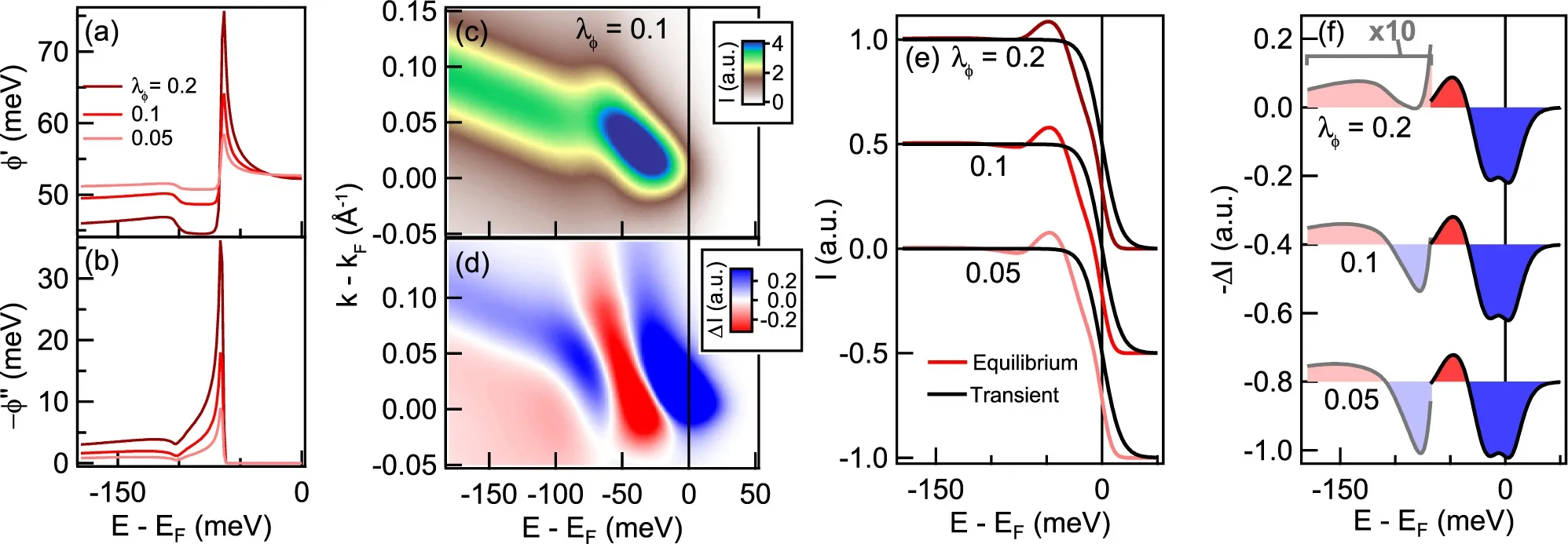
图19.用Eliashberg公式模拟的ARPES强度,考虑玻色子能量为35 meV,耦合强度为λZ=1,以及各向异性的λϕ。(a)和(b)分别为ϕ在20 K下的实部和虚部,为了固定超导能隙保持30 meV增加了一个常数ϕ′;(c)λϕ=0.1时的ARPES强度谱图;(d)泵浦前后ARPES图谱强度的改变量,瞬时态图谱的模拟条件为ϕ=0和T=80 K;(1)通过式(3)计算得到的平衡态和瞬时态的动量积分强度[86]

图20.在节点方向非平衡态激发电子的重组时间。(a)时间延迟为 −1.2 ps下的 ARPES原始图谱和时间延迟为 0 ps与 0.9 ps下的强度改变量;(b)不同时间延迟下对ARPES原始图谱做整个动量范围内的强度积分曲线,图中插图为箭头处的放大图;(c)超导态和正常态下∆Ie随时间延迟的变化关系和超导态下最大能隙以上的∆Ie随时间延迟的变化关系
为了更好的理解这种积聚现象,考虑非平衡态积聚的动量依赖关系。在动量空间中,相似的积聚延迟也同样在费米弧区域中被观察到。图21(a)显示了最佳掺杂样品在弱泵浦通量下(2.4µJcm−2)积聚时间的动量依赖关系。可以看到皮秒尺度下的非平衡态准粒子数衰减速率(γ)随着远离节点而不断增大;同时在费米弧区域内存在着积聚的时间延迟,并且这个延迟随着远离节点而不断减小。而在费米弧区域以外并没有观察到时间延迟,tbuildup衰减与正常态一般大小。在过掺杂78 K样品中同样进行了动量依赖关系的测量,也发现了相似的动量依赖关系。但是对于过掺杂样品来说所有的动量测量线均穿过费米弧区域,因此均能明显地观测到积聚的时间延迟。此外,过掺杂样品相比于最佳掺杂和欠掺杂样品积聚所需的时间更少(图21)。
对于欠掺杂Bi2212样品,发现在超导态下不同泵浦通量下非平衡态的积聚在临界通量 (13µJcm−2)前后会有着很大的不同(图22(a))。特别是在通量为24µJcm−2时几乎和正常态时一样∆Ie(t)瞬间就达到了最大值,而在能达到的最低泵浦通量下需要0.9 ps才能达到最大值。对于正常态(T=90 K),在任何通量下非平衡态准粒子数几乎不需要任何积聚便达到了最大值 (图22(b))。为了更精确的提取tbuildup,可以通过卷积一个分辨率函数来进行拟合:

其中γ为非平衡态准粒子在皮秒尺度下的衰减率,高斯函数则由仪器分辨率所决定,其半高宽(FWHM)为300 fs。提取出来的tbuildup如图22(c)所示。可以看到在超导态下最低通量时tbuildup为∼400 fs,随着泵浦通量的增加,tbuildup不断减少最终趋于稳定(<100 fs)。而饱和状态发生在泵浦通量大于临界通量时,也就是泵浦完全抑制超导凝聚的时候。值得注意的是,超导能隙在0.6 ps前并没有关闭[80]。在高于临界温度和泵浦通量时几乎不需要积聚时间说明了这种缓慢积聚的现象和超导凝聚之间有着某种联系。

图21.重组时间的动量依赖关系。(a)在不同动量测量线下,最佳掺杂Bi2212样品的∆Ie随时间延迟变化关系;(b)在不同动量测量线下,过掺杂78 K Bi2212样品的∆Ie随时间延迟变化关系;(c)节点处重组时间的掺杂依赖关系。
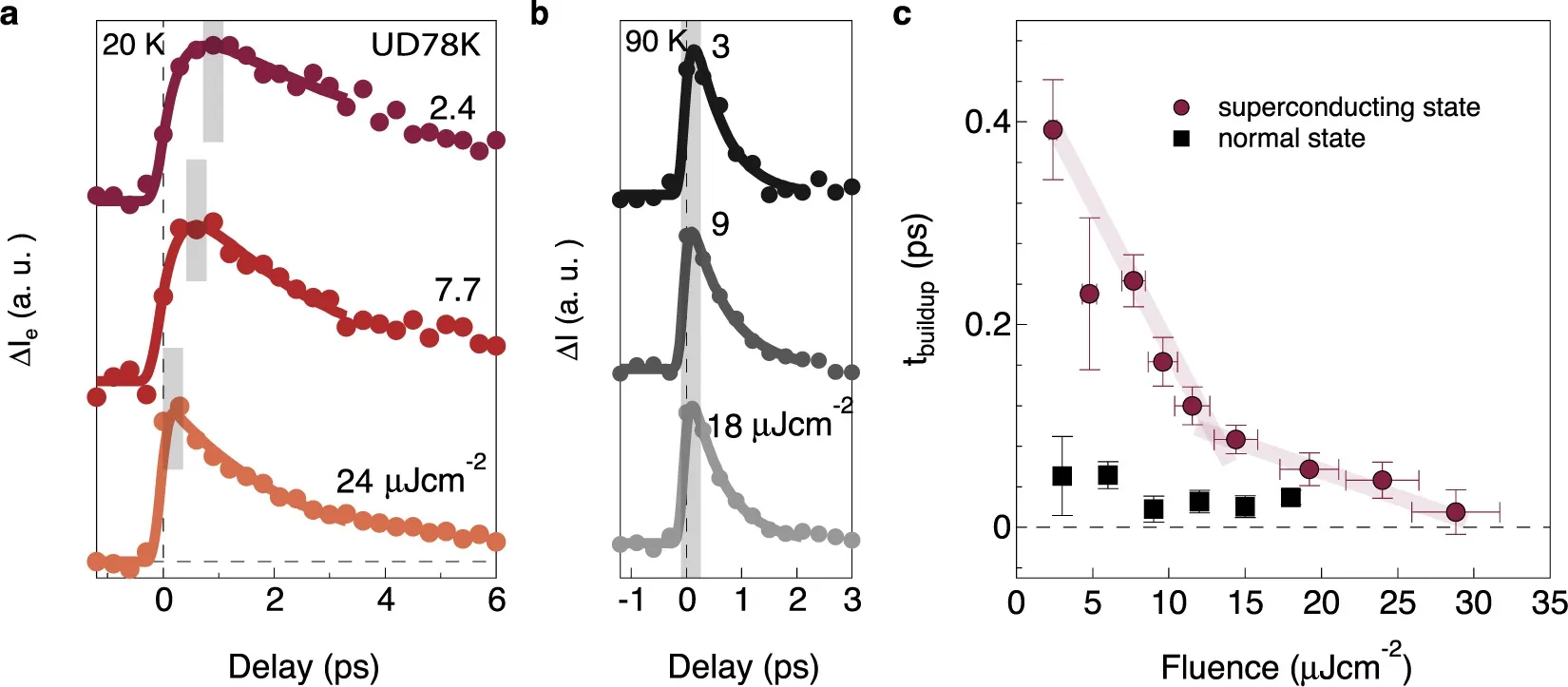
图22.节点方向重组时间的泵浦通量依赖关系。(a)不同泵浦通量下超导态欠掺杂78 K样品的∆Ie随时间延迟的变化关系;(b)不同泵浦通量下正常态欠掺杂78 K样品的∆Ie随时间延迟的变化关系;(c)从(a)中提取的重组时间tbuildup与泵浦通量的关系。

图23.超导体对低于和高于临界通量的泵浦激光的响应
可以用量子相干的库珀对凝聚来解释这一现象,当泵浦脉冲激发了材料,入射的能量部分存在电子中,部分存在晶格中[94,95,96]。当发生超导凝聚时,如果互为时间反演对称的非平衡态准粒子均被激发,这些粒子就能够通过与现有的库珀对发生相干受激重组而快速地重组为新的库珀对。这个过程会减少最初存储在电子自由度中输入能量的比例,从而会观测到非平衡态准粒子数需要积聚一段时间才能达到最大值。这个受激重组过程会由于温度和过高的泵浦通量抑制超导凝聚而消失。在tbuildup后,剩下的均是未配对的激发态准粒子,也就是说与其成时间反演对称性的粒子没有被激发。在更长的时间尺度上由于杂质引起的动量变化,这些无法配对的激发准粒子会重新演变为互成时间反演对称从而快速重组。这一重组过程因为受到从不能配对的非平衡态准粒子演变为可以互相配对的非平衡态准粒子速率的影响往往有着前面所说的“瓶颈效应”,这个过程可以用实空间bimolecular recombination model来进行描述。图23很好的描述了这一具体过程。但是由于Bi2212样品的中电子的不均匀性,动量守恒应该放宽,即当“配对”的非平衡态准粒子重新组合时,它们可以发射出一定动量范围内的声子(玻色子)。在这种情况下,tbuildup动量依赖性可以很容易地由重组速率 (γ)的动量依赖性来解释,其值随着离开节点而增加。
值得注意的是,在库珀对受激辐射的过程中,由于准粒子能量的降低,必然释放相应能量的玻色子。这些玻色子直接参与了配对过程,但是这是否是与超导配对的机制存在关联还需要进一步的研究。
IV.讨论总结
经过多年的研究,在铜氧化超导体中发现了许多奇异的多体相互作用,但机制至今还不清楚,比如多体相互作用导致能带扭折的起源是声子、磁振子亦或是其他玻色子至今仍无法得到有效的证实。另外,在传统超导体图像中如果在正常态下电子–玻色子耦合能量为Ω则在进入超导态后会移至 ∆+Ω[36],而在铜氧化物超导体中却没有观察到这种现象。最重要的是,目前所发现的铜氧化物中多体相互作及其复杂的动量依赖关系是否与超导配对存在关联或者是否在超导配对机制中起重要作用仍是目前多体效应研究中的重点。
随着trARPES技术的不断发展,其在谱函数上新增了时间的维度、能够同时探测占据态和非占据态的信息等优点使其在研究铜氧化物超导体电子结构上提供了一个全新的视角。TrARPES实验的一个重要因素是泵浦光子能量,如果将来技术上能实现THz泵浦共振激发铜氧化物超导中的玻色集合模式,将对非平衡态准粒子的动力学、超导能隙动力学、多体相互作用动力学研究带来重要进展,也将从非平衡单粒子谱函数去直接验证是否存在激光诱导的非平衡态高温超导现象。对于多体相互作用的研究,利用trARPES结合其他对晶格超快动力学研究实验手段(超快X射线衍射,超快电子衍射),结合可能存在的非平衡态高温超导现象,将为理解高温超导配对机制提供重要线索,为探索转变温度更高的超导现象提供指引。
