永磁同步电机磁链观测改进积分方法的研究

张 乐，杨 强

(无锡太湖学院，无锡 214064)

0 引 言

近年来，在以新能源汽车和高铁为代表的新型电力牵引技术中，永磁同步电机具有大功率密度、高效率、高可靠性以及结构简单等优点，引起了国内外学术界的广泛关注[1-2]。同时在线观测系统作为电机控制中的重要部分也已经成为了研究热点，实时性好、准确率高的状态监测系统对于电机驱动控制的效果以及系统故障的排查都具有至关重要的作用[3-4]。

直接转矩控制(以下简称DTC)是直接以转矩为控制对象，通过转矩和磁链滞环控制器结合定子磁链的扇区选择空间电压矢量完成对电机的驱动控制，其中磁链滞环控制以及定子磁链的扇区判断都需要对电机系统的定子磁链进行观测。传统的磁链观测包括电压模型和电流模型两种观测方法，而电流观测模型与电机的永磁体磁链，交直轴电感以及位置信号都直接相关，随着电机运行过程中参数发生变化很难准确地观测定子磁链；而电压观测模型则采用的是反电动势积分方法，对电机参数依赖较小，鲁棒性高，因而得到了广泛的关注[10]。但是传统DTC定子磁链的电压观测模型涉及到积分方法的问题，虽然纯积分器计算方法简单，但是存在积分初值的问题，导致结果发生偏差。除此之外，对于传统的纯积分方法，如果输入反电动势信号中有一个直流偏置，那么在积分得到的磁链观测结果中将会叠加一个随时间线性增加的偏置信号，随时间的累加必会导致积分器的饱和[5]。

为了解决传统磁链观测器存在的问题，肖曦等学者研究通过卡尔曼滤波器对永磁磁链进行较高精确度的在线辨识，但是并没有在理论上给出在运行过程中电机参数发生变化时对观测器的影响以及对应的解决办法，而且这种观测方法实际实现起来也有一定的难度[6]。同样的，周扬忠等提出的利用基于“有效磁链”的滑模磁链观测器进行磁链观测的方法，也没有进一步分析电机参数变化时，磁链观测的精度会发生什么样的变化[7]。此外，还有学者通过波波夫(Popov)超稳定性定理以及李雅普诺夫(Lyapunov)定理对观测系统的稳定性进行证明，但是在此基础上并没有对观测器的收敛性在定量上进行更加细致的分析[8-9]。

本文是对传统的纯积分器积分方法进行改进，对一阶惯性滤波积分方法以及幅值限定补偿的改进积分方法进行对比分析，从而找到能够在更大转速范围内对定子磁链进行较为准确跟踪的方法，对观测系统进行了定量的分析。通过仿真和实验验证了幅值限定补偿的改进积分方法能够有效提高永磁同步电机DTC下的磁链估计的精度。

1 DTC磁链观测方法分析

1.1 DTC基本原理

DTC是直接以转矩为控制对象，首先通过转速外环得到转矩给定，然后通过转矩和磁链的滞环控制器结合扇区判断从开关表中选择空间电压矢量作用，进而实现直接控制电机转矩的控制方法，图1为对应的DTC简化控制框图。

图1 DTC系统简化控制框图

对应的传统DTC的扇区划分如图2所示，虚线表示扇区边界。

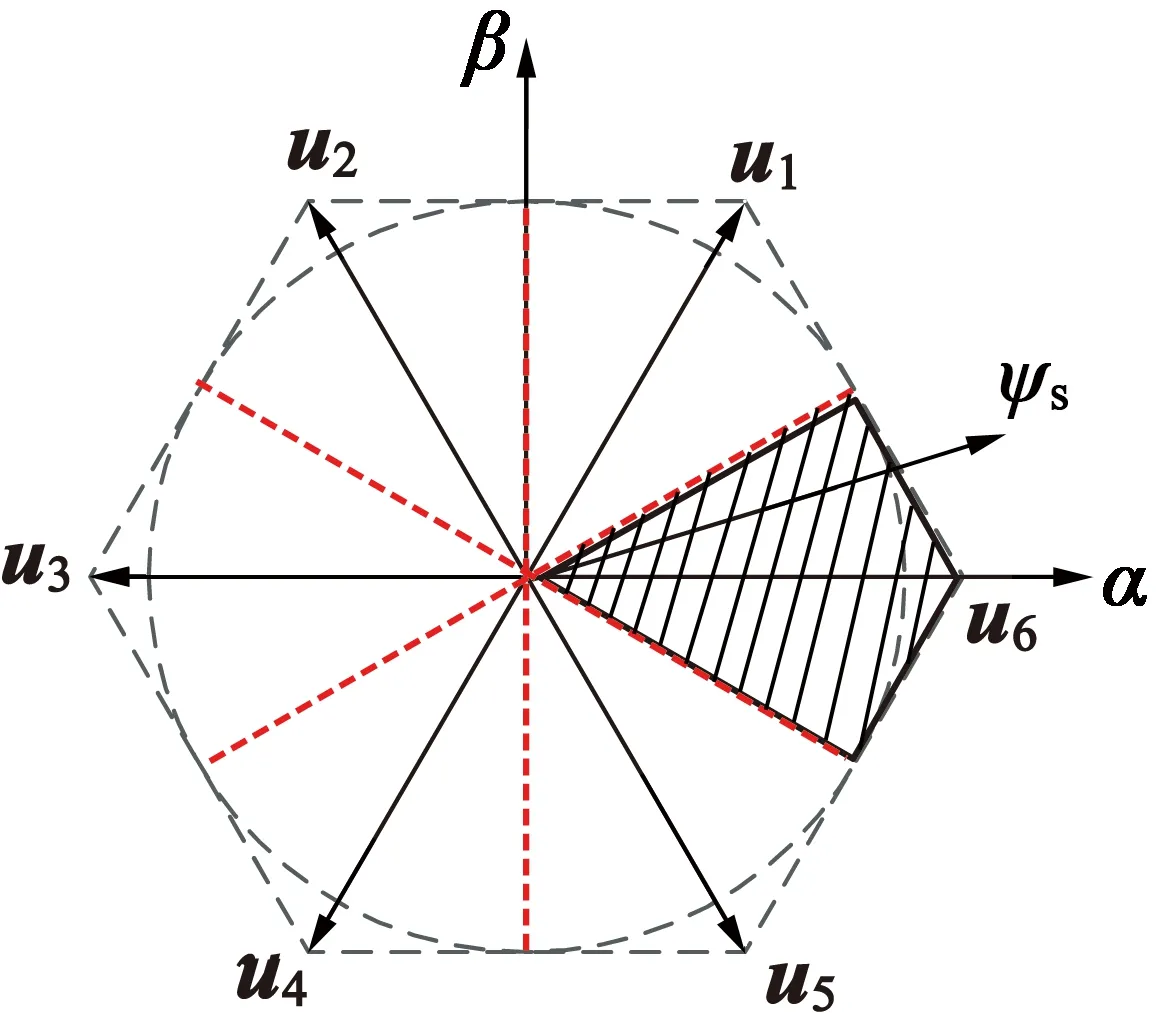
图2 传统DTC扇区划分

该系统中扇区的判断是首先在两相静止αβ坐标系中对定子磁链进行计算，定义：

(1)

然后根据式(2)判断扇区:

N=4f(a)+2f(b)+f(c)

(2)

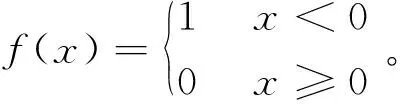
可见，扇区判断的准确性直接由磁链观测的准确性决定，所以有必要对定子磁链的观测问题进行研究。

1.2 永磁同步电机的传统磁链观测方法

根据永磁同步电机的基本数学模型，结合通过测量得到的电机绕组电流及其永磁磁链值，其定子磁链的电流观测模型可以推导:

(3)

式中：ψsd，ψsq分别为直轴和交轴磁链；Ld，Lq分别为直轴和交轴电感；id，iq分别为直轴和交轴电流；ψf为永磁磁链。可见，定子磁链的电流观测模型需要电机系统的交直轴电感，永磁体磁链以及准确的转子位置信号，对参数的依赖较大，在温升等电机参数发生变化的情况下，观测结果往往不够精确。

而根据定子电压检测的磁链的电压观测模型如下：

(4)

式中：ψsα，ψsβ，Usα，Usβ，isα，isβ分别为定子静止两相坐标系下的定子αβ轴磁链、电压和电流；R为定子绕组内阻。电压观测模型中的相电压参数是通过开关表状态结合母线电压计算得到的：

(5)

式中：UA，UB，UC分别为三相绕组的相电压；SA，SB，SC为驱动变换器的三相桥臂的开关状态；Udc为驱动直流电源电压。可见，定子磁链的电压观测模型只需要电机的电阻参数，对电机参数的依赖较小，鲁棒性高。但是在低速运行时，这种观测方法由于受电阻参数的影响，观测精度较差。除此之外，电压观测模型的最关键问题就是积分方法，传统DTC定子磁链的电压观测模型采用的是纯积分器。由于磁链观测是对电机定子绕组的反电动势进行积分，反电动势是一个正弦量，由于该正弦量初始角度的问题，当纯积分器对其进行积分时往往会存在一个幅值随初始位置变化而变化的直流偏移量，而且当反电动势信号中存在一个直流分量时，纯积分器得到的磁链观测结果会存在一个随时间线性增加的偏置，这必然会造成积分器的饱和。

1.3 磁链观测器的改进方法

针对传统DTC中定子磁链电压观测模型中纯积分器存在的这些问题，本文提出可以通过对电压观测模型中的积分方法进行优化。

首先针对由于纯积分器对初始位置的敏感性而带来的积分结果的直流偏置，可以在传统纯积分器的基础上增加一个高通滤波器滤除直流分量，对应的传递函数:

(6)

将其进行简化之后得到一阶惯性滤波器:

(7)

高通滤波器阻断低频信号，由高频信号的特性可知，通过这种积分方法能够滤除结果中直流偏置。但是同时当反电动势信号频率比较低，也就是电机转速比较低时，由于高通滤波器的幅频和相频特性:

(8)

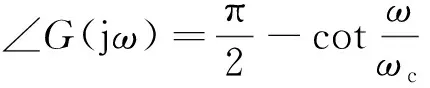
(9)

观测得到的定子磁链同样会存在幅值衰减和相位前移的问题。

针对这种简单增加高通滤波器带来的问题，本文通过增加一个反馈通路来补偿由于高通滤波器的幅频和相频特性带来的观测结果的幅值衰减和相位前移。对应的控制系统框图如图3所示。

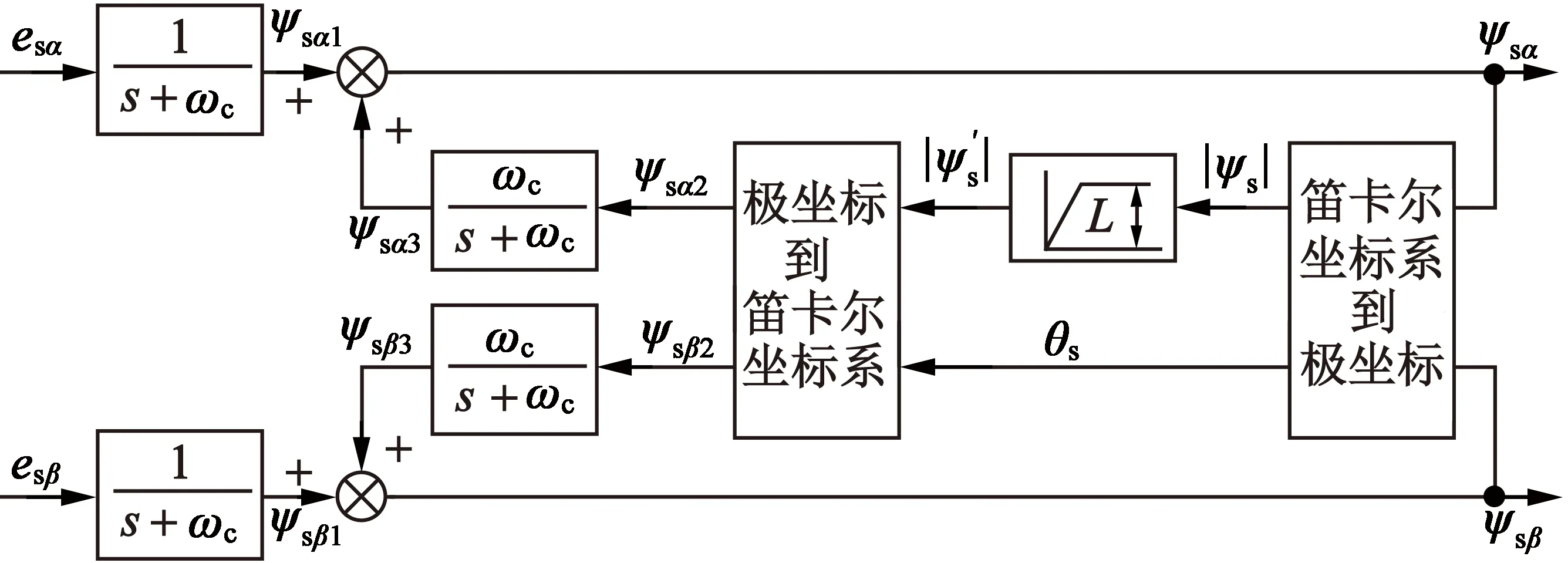
图3 幅值限定补偿改进积分器控制框图

由图3可见，前向通道仍然是一个一阶惯性滤波器，而添加的反馈通道首先通过笛卡尔坐标系和极坐标系的来回转换起到保持输出磁链相位角的作用；同时通过限幅环节抑制一阶惯性滤波器在输入低频信号时存在的幅值衰减问题，对应的限幅环节的限幅值一般设置为电机定子磁链给定值，由此得到系统的传递函数：

(10)

再由反馈通道的传递函数可以看出，当输入高频反电动势信号时，其增益为零，反馈通道不起作用。当输入低频反电动势信号时，如果观测到的定子磁链幅值小于限幅值时，反馈通道的磁链幅值等于前一时刻观测到的磁链幅值，此时：

(11)

这种情况下，改进的积分器类似于一个纯积分器，但是又由于前向通路中包含了一个高通滤波器，所以同样能够抑制观测的磁链结果中的直流偏置。

如果观测到的定子磁链幅值大于限幅值，那么反馈的磁链幅值等于限幅值：

(12)

同样能够观测到定子磁链的准确值。

综上所述，幅值限定补偿改进积分器不仅能够抑制传统纯积分器中由于初始位置角引起的定子磁链观测结果的直流偏移量，而且相比于一阶惯性环节还能够在低转速情况下，解决幅值衰减和相位前移的问题，所以基于幅值限定补偿的改进积分器是一种在宽转速范围下能够精确观测永磁同步电机定子磁链的积分方法。

2 仿真分析

在MATLAB下对传统纯积分器以及改进之后的两种积分方法进行对比仿真，并在此基础上，对定子磁链电压观测模型的两种改进积分方法在DTC系统中的实际控制效果进行对比仿真，以此对两种改进积分方法的实用性进一步分析。

2.1 积分方法对比仿真

以α轴为例，通过给定高频和低频两种不同情况的反电动势信号，分别经过纯积分器、一阶惯性积分器以及幅值限定补偿改进积分器，对比它们的输出结果。假设给定的反电动势信号：

esα=ωψsαsin (ωt)

(13)

式中：ω为输入反电动势信号的电角频率；ψsα为定子磁链的α轴分量。可见经过纯积分器可得：

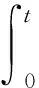
(14)

纯积分器观测到的定子磁链中包含了一个幅值为1的直流偏置，在此理论分析的基础上，设置改进积分器的截止角频率均为ωc=10 rad/s。当输入高频反电动势信号ω=1 000 rad/s时，得到α轴定子磁链波形如图4所示。

可见，在高频反电动势输入信号之下，只有纯积分器的观测结果中包含了幅值为1的直流偏置，与理论值一致，而一阶惯性滤波器和幅值限定补偿改进积分器都抑制了直流偏移量，且一阶惯性滤波器的积分结果没有出现幅值衰减和相位前移的问题。

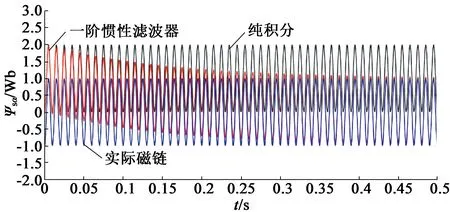
(a) 一阶惯性滤波器磁链观测效果对比

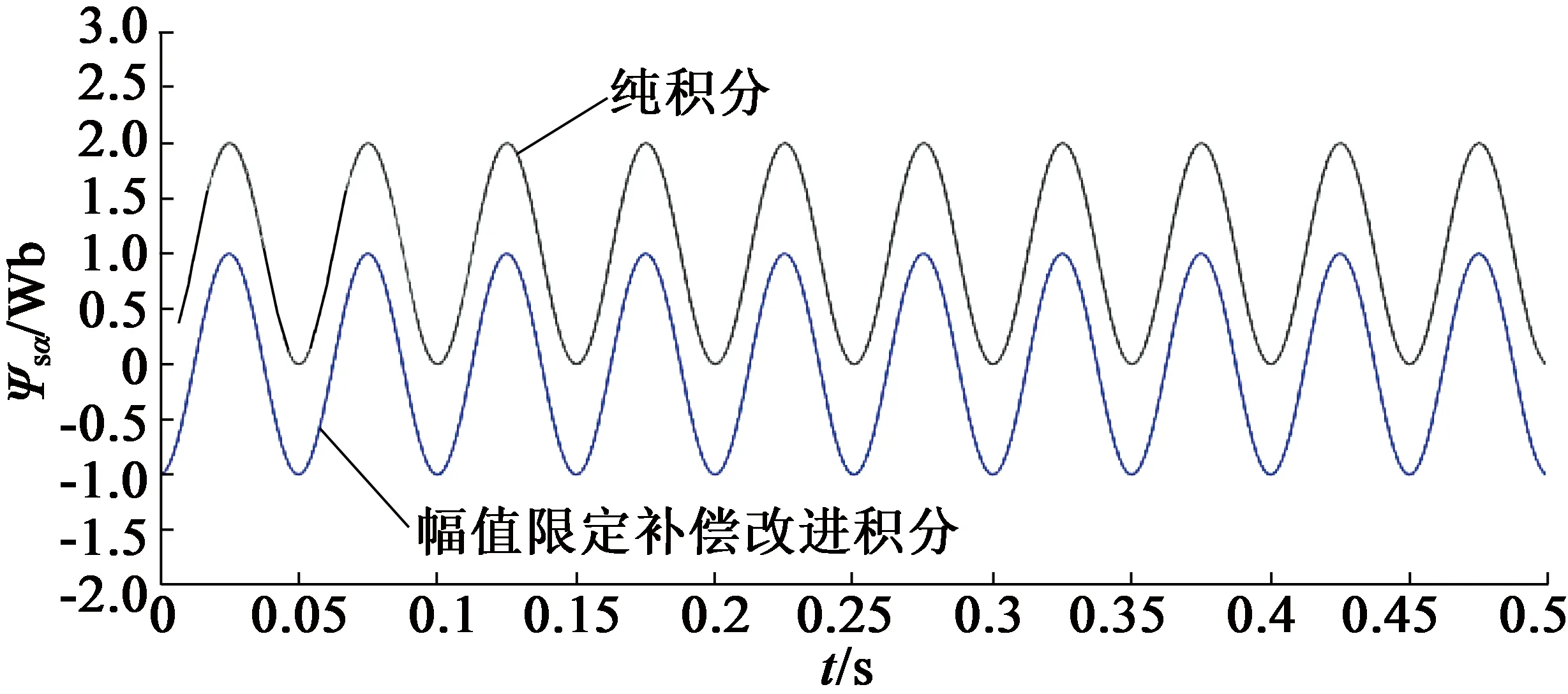
(b) 幅值限定补偿改进积分器的磁链观测效果对比

根据ω=1 000 rad/s时的传统积分方法和两种改进积分方法的仿真波形，得到ω=1 000 rad/s时的观测性能对比，如表1所示。

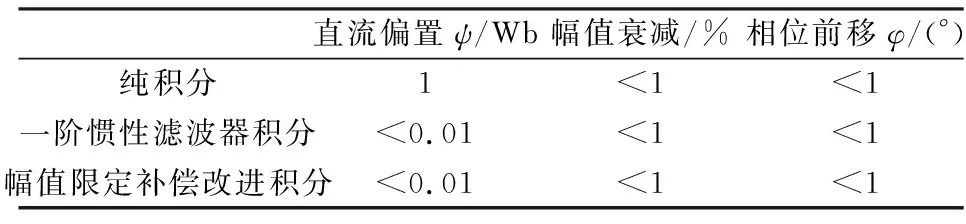
表1 ω=1 000 rad/s时不同积分方法的性能对比

当输入低频反电动势信号ω=20 rad/s时，得到三种不同积分方法下的定子磁链观测的仿真结果，如图5所示。

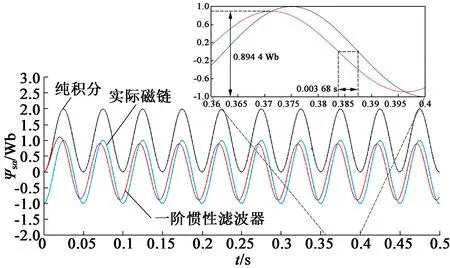
(a) 一阶惯性滤波器磁链观测效果对比

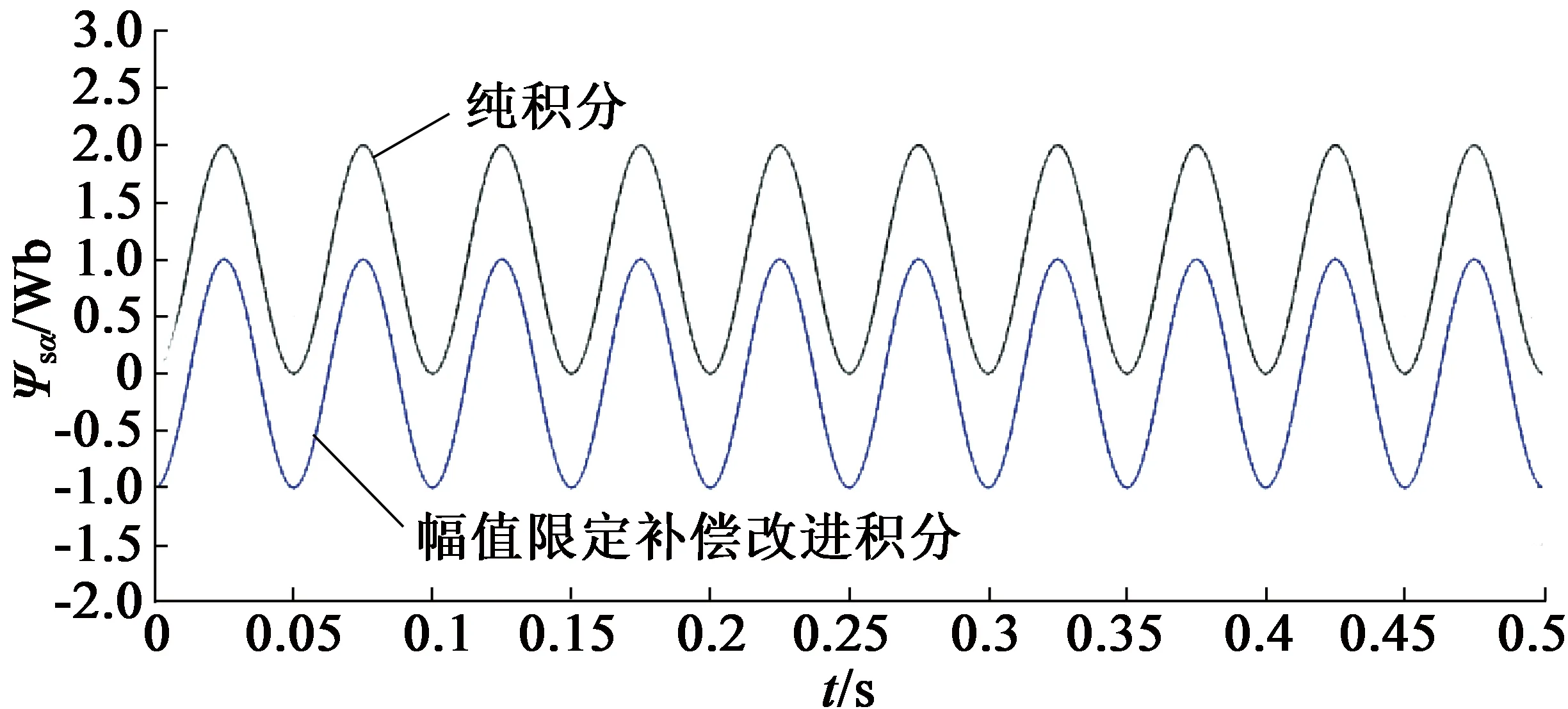
(b) 幅值限定补偿改进积分器的磁链观测效果对比

由输入低频反电动势信号时的仿真波形可以看出，纯积分器会产生的直流偏置，两种改进积分器都能够起到抑制作用，但是一阶惯性滤波器的积分结果明显发生了幅值衰减和相位前移，结合高通滤波器的幅频和相频特性得到理论值：

(15)

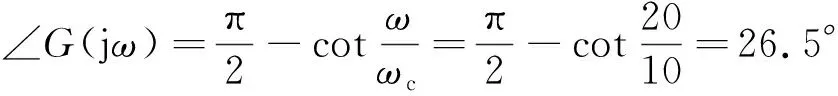
(16)

对比仿真结果可以发现，仿真波形中的磁链幅值衰减到了0.894 4Wb，与理论值基本一致，而相位前移值的时间刻度为0.003 68s，结合此时的周期0.05s，得到相位前移的角度为26.52°，与理论值也基本一致。而幅值限定补偿改进积分器无论对于高频或者低频信号都能够准确跟踪实际磁链，有比较好的观测性能。由此得到传统纯积分器，一阶惯性滤波器积分以及幅值限定补偿改进积分器在ω=20 rad/s时的观测结果对比，如表2所示。

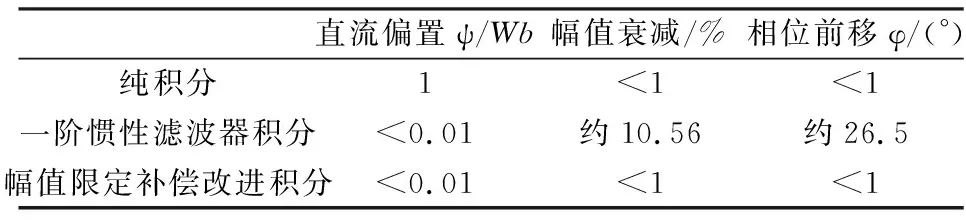
表2 ω=20 rad/s时不同积分方法的性能对比

2.2 改进积分方法在DTC系统中的仿真分析

考虑到两种改进积分方法对高频反电动势信号的积分都有较好的效果，仅在低频时存在差异，所以两者在DTC系统中的仿真也在低频，也就是在电机转速较低的情况下进行对比仿真。由于仿真情况下，电机参数的准确性得到保障，且不考虑电机参数的变化，所以电流模型观测到的定子磁链可以认为是实际值，从而可以将基于两种改进积分器的电压观测模型的磁链观测结果与电流观测模型的观测结果进行对比，比较两者的观测性能。

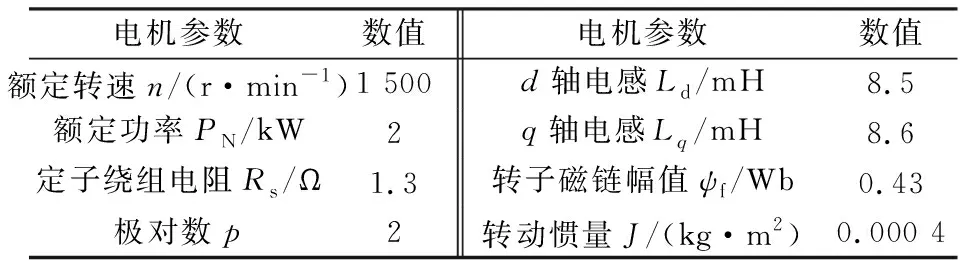
表3 实验用永磁同步电机参数

由此得到在DTC系统下，电流观测模型和基于两种改善积分器的电压观测模型的磁链观测仿真结果如图6所示。

在电机转速600 r/min下，输入反电动势信号电角频率为ω=20 rad/s。由仿真结果可以看出，基于幅值限定补偿改进积分器的电压观测模型的观测结果与电流观测模型得到近乎实际值的结果基本一致，有较好的观测性能。而基于一阶惯性滤波器的电压观测模型所观测到的定子磁链存在明显的相位前移和幅值衰减问题。根据仿真结果的细节波形发现，定子磁链的幅值衰减为0.388 Wb，相比于给定定子磁链0.43 Wb衰减了9.77%，而相位前移的时间刻度为0.003 68 s，结合此时的电压电流周期0.05 s可知，相位前移角度约为26.5°，可见仿真结果的误差值与理论分析值基本一致。

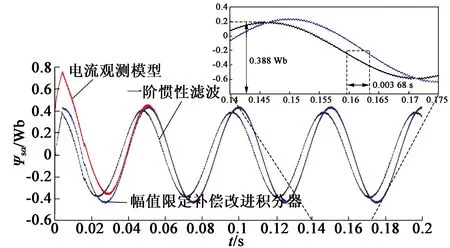
图6 不同积分方法在DTC系统中的对比仿真波形

将两种改进积分方法的磁链观测结果分别应用到DTC系统中，分别得到两者的扇区计算对比波形和转矩的对比波形，如图7，图8所示。

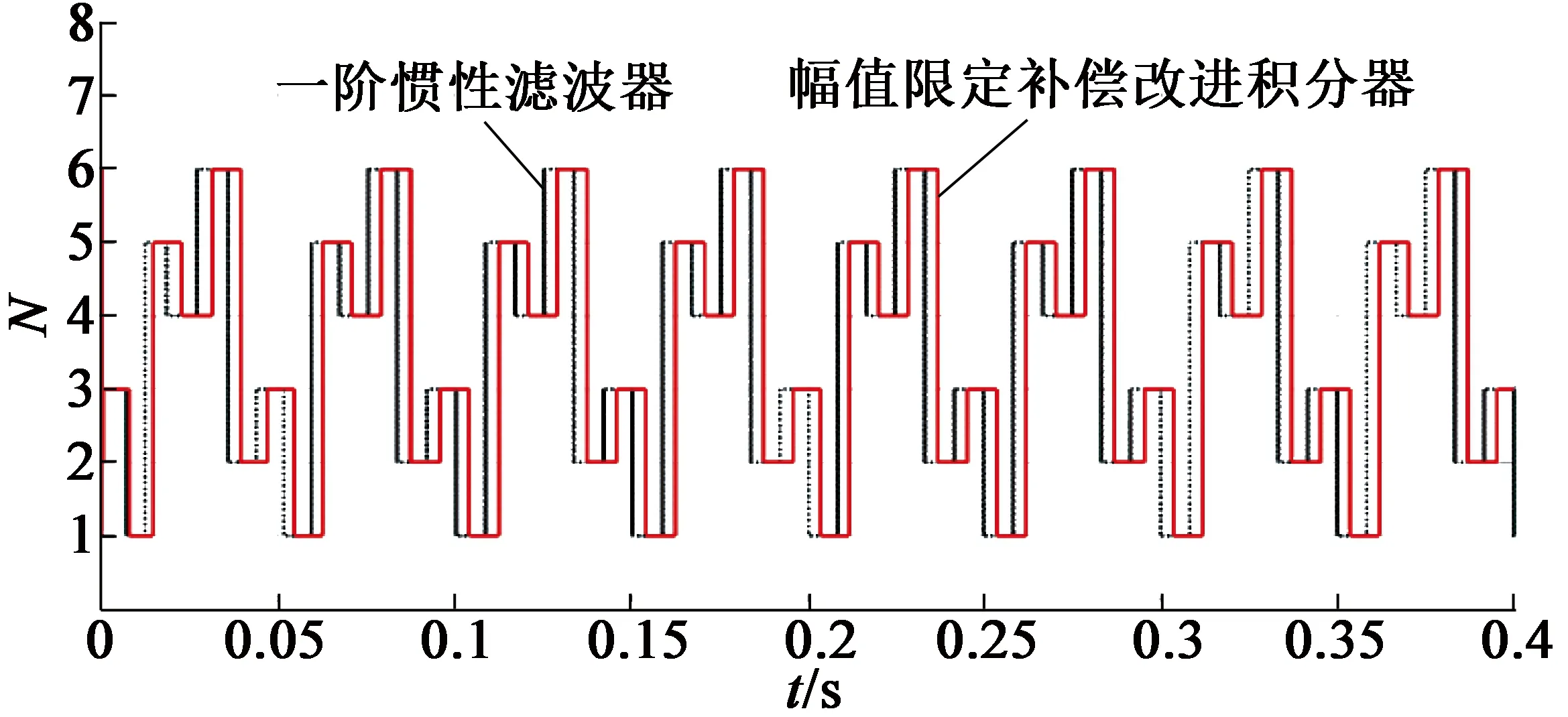
图7 两种改进积分方法在DTC系统中的扇区划分对比波形

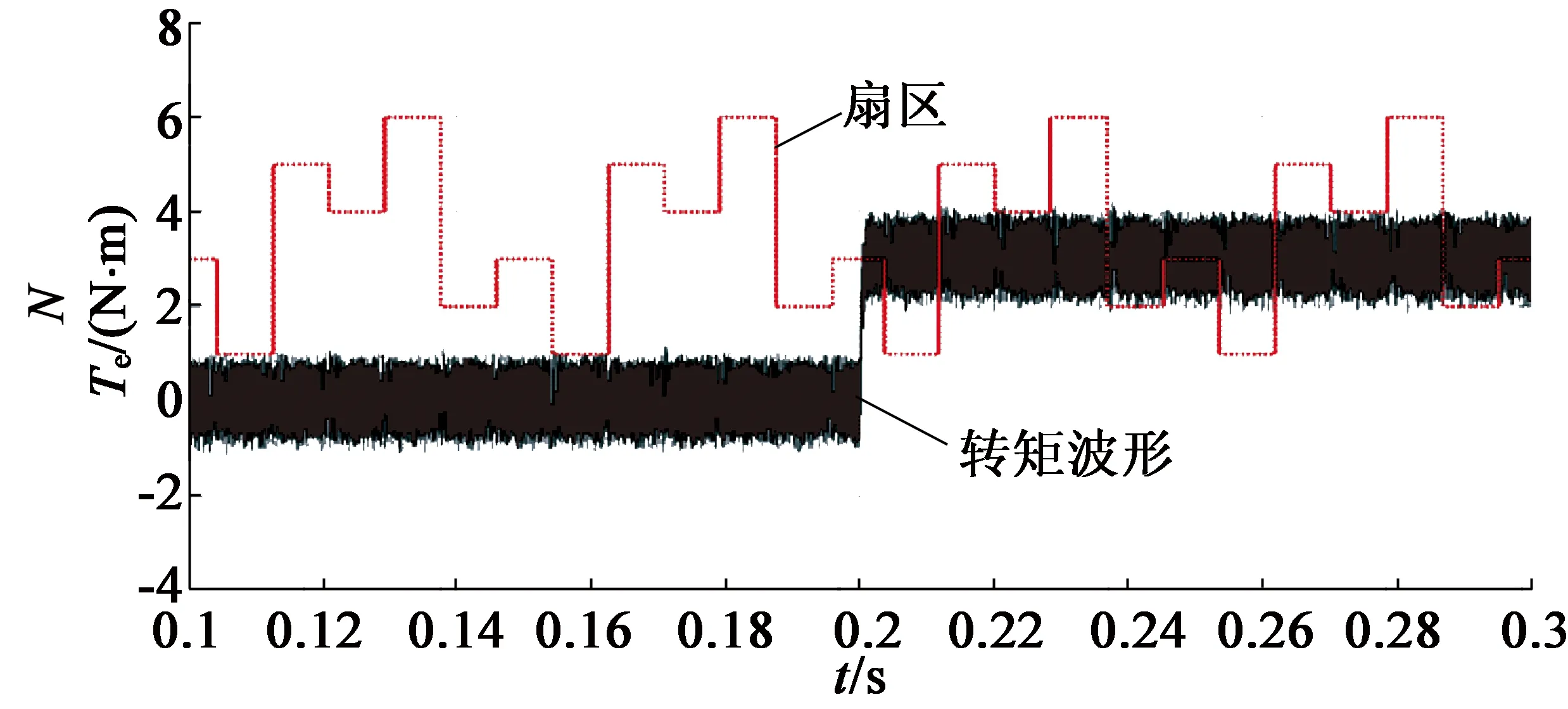
(a) 基于幅值限定补偿改进积分器DTC系统的扇区与转矩波形图

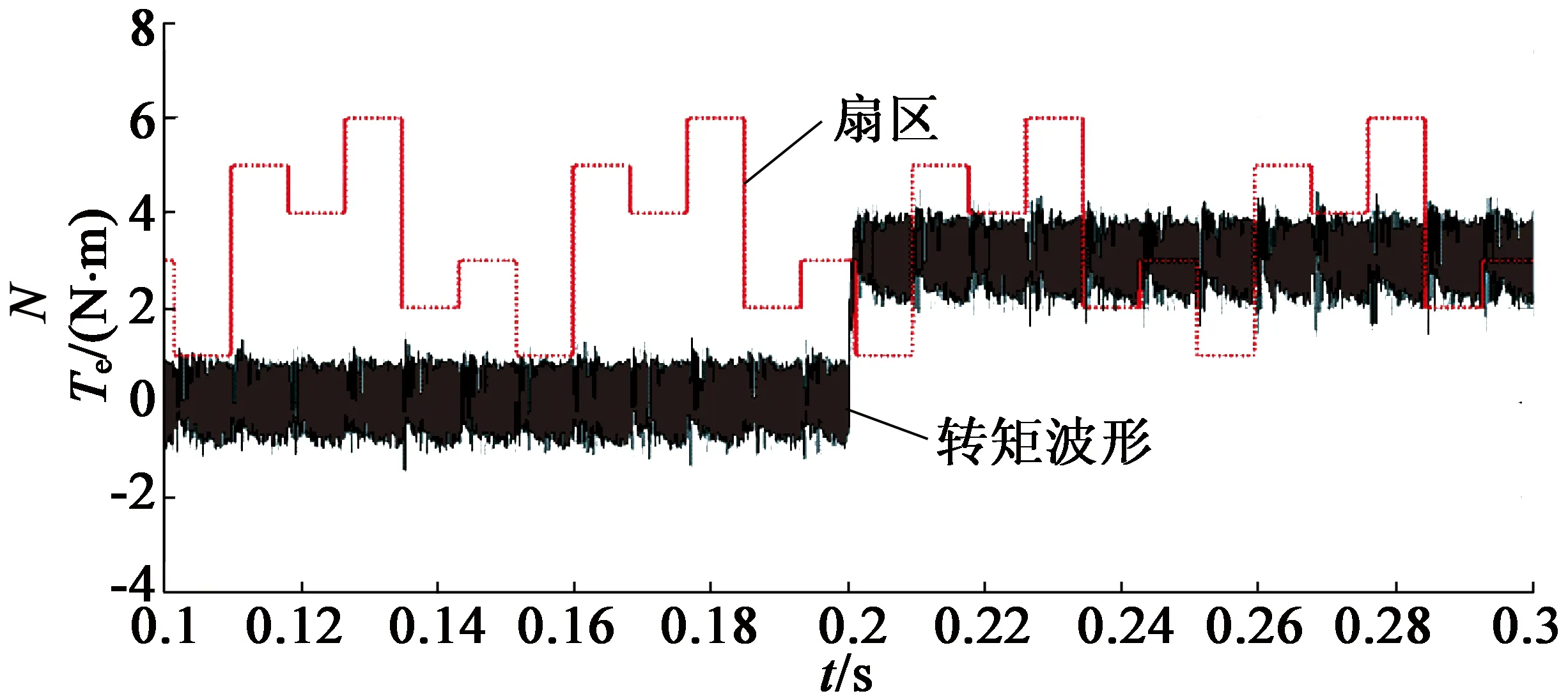
(b) 基于一阶惯性滤波的DTC系统的扇区与转矩波形图

根据图7两种改进积分方法下的扇区划分对比波形可见，由于在电机低速运行时，一阶惯性滤波器积分结果存在一定程度的幅值衰减和相位前移造成定子磁链观测结果存在误差，进而引起了扇区划分也相比于实际的扇区存在对应的误差，由仿真结果来看，应用一节惯性滤波器的DTC系统的扇区划分超前于实际扇区一定的时间。

根据图8两种改进积分方法下的扇区与转矩的对照波形的对比发现，由于一阶惯性滤波器的扇区划分与实际扇区存在误差，导致了电机的电磁转矩在扇区切换附近的脉动明显增大，达到了约±1.4N·m；而应用幅值限定补偿改进积分的DTC系统由于能够较为准确地观测到定子磁链，在各个扇区切换点上的转矩脉动并没有明显变化，转矩脉动基本一直维持在±1 N·m左右。

综上所述，相比于传统纯积分器，一阶惯性滤波器通过引入高通滤波器能够对直流偏移量起到比较好的抑制效果，电机高速运行时的观测精度有一定的保证。但是在电机低速运行时，同样由于高通滤波器的幅频和相频特性，会造成磁链观测结果的幅值衰减和相位前移问题。针对一阶惯性滤波器存在的问题，幅值限定补偿改进积分器能够通过增加一个反馈通路，在电机低速运行状态下将高通滤波器所产生的不利影响进行有效抑制，从而实现更宽转速范围下的定子磁链的高精度观测。

3 实验验证

为了验证优化策略的有效性，在基于C28335芯片的驱动控制实验平台上对传统纯积分器、一阶惯性滤波器以及幅值限定补偿改进积分器三种磁链观测方法进行实验比较研究，电机参数与仿真所用电机参数一致。

给定磁链幅值为0.43 Wb，反馈磁链饱和限幅值0.43 Wb，两种积分方法的截止频率设置为ωc=3 rad/s，给定转速150 r/min，控制周期100 μs。在低转速150 r/min的条件下，分别对比了一阶惯性滤波和幅值限定补偿的改进积分器两种定子磁链的电压观测模型与电流模型的观测结果，图9为一阶惯性滤波积分方法下的磁链观测对比实验波形。图9中波形的标识分别为基于一阶惯性滤波积分的电压观测模型的结果，以及电流观测模型的结果。在低速运行时，通过较为准确的电机参数在电流观测模型下得到的定子磁链也较为准确，这里认为是实际磁链。

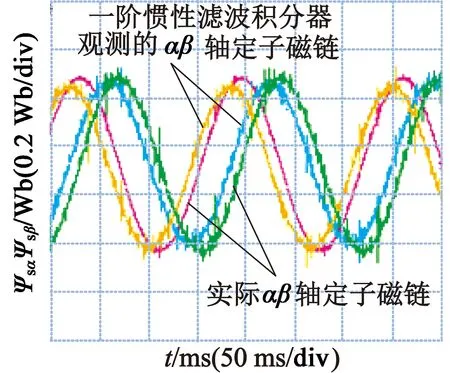
(a) 整体实验波形

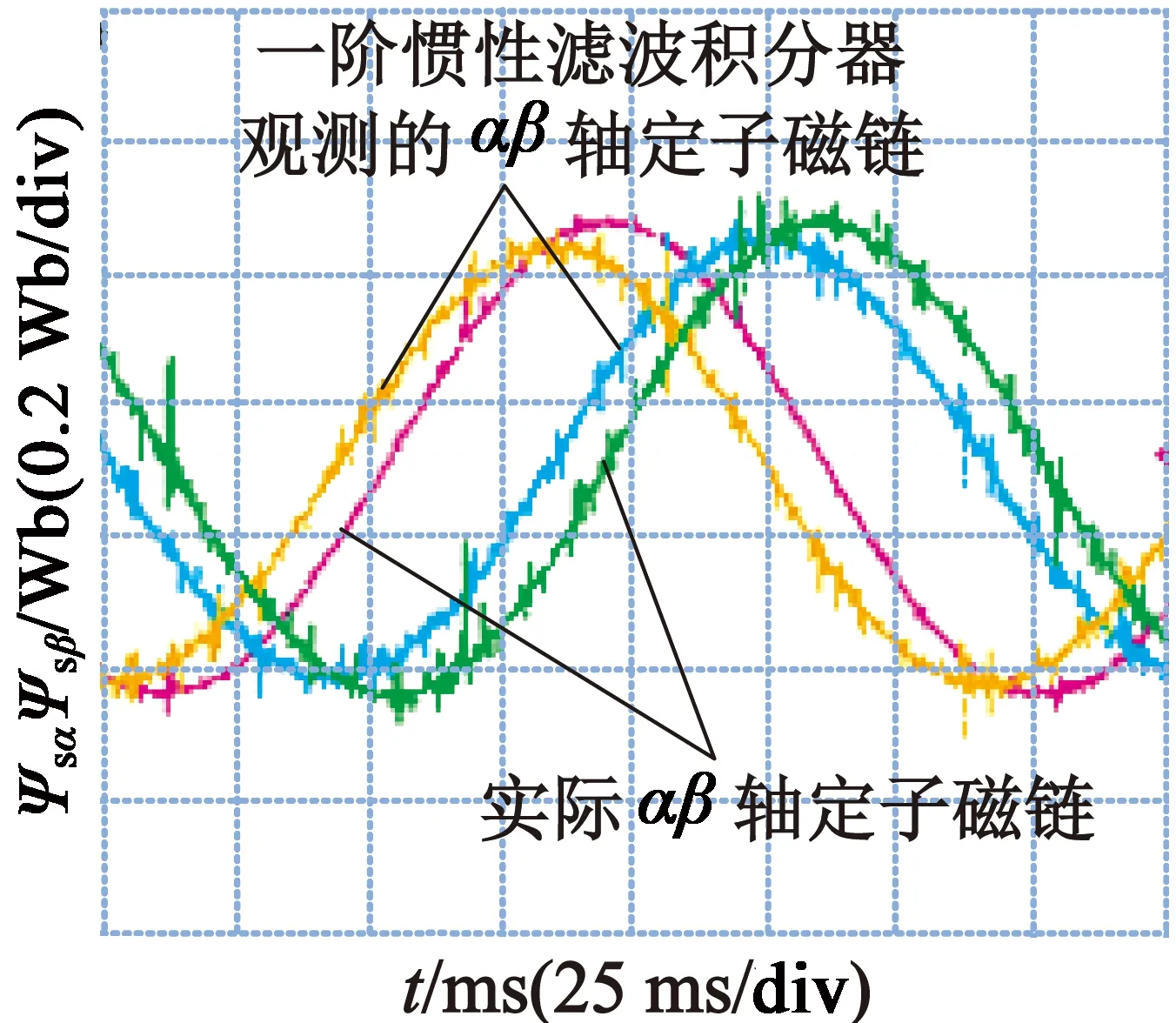
(b) 细节波形

由图9可以看出，在低速运行时基于一阶惯性滤波积分的电压观测模型的结果明显存在幅值衰减和相位超前的问题，与理论分析和仿真结果相对应。实际磁链幅值即为给定定子磁链幅值为0.43 Wb，而基于一阶惯性滤波积分器的电压观测模型所观测到的αβ轴磁链的幅值约为0.38 Wb，衰减11.62%，而相位前移了约12.5 ms，结合此时的电压电流周期200 ms可知，相位前移了约22.5°。

基于幅值限定补偿的改进积分器的电压观测模型的磁链观测结果对比波形如图10所示。

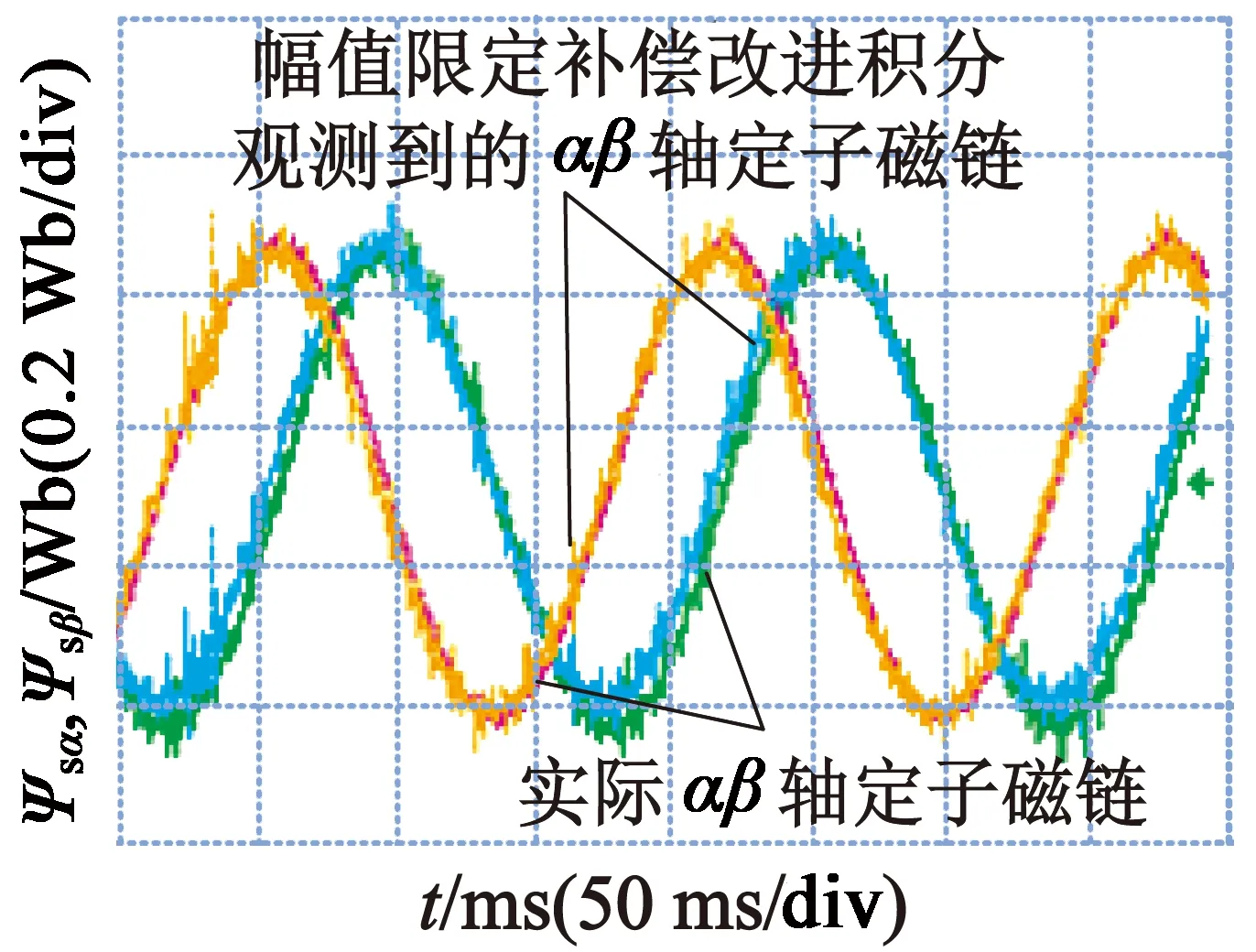
(a) 整体实验波形

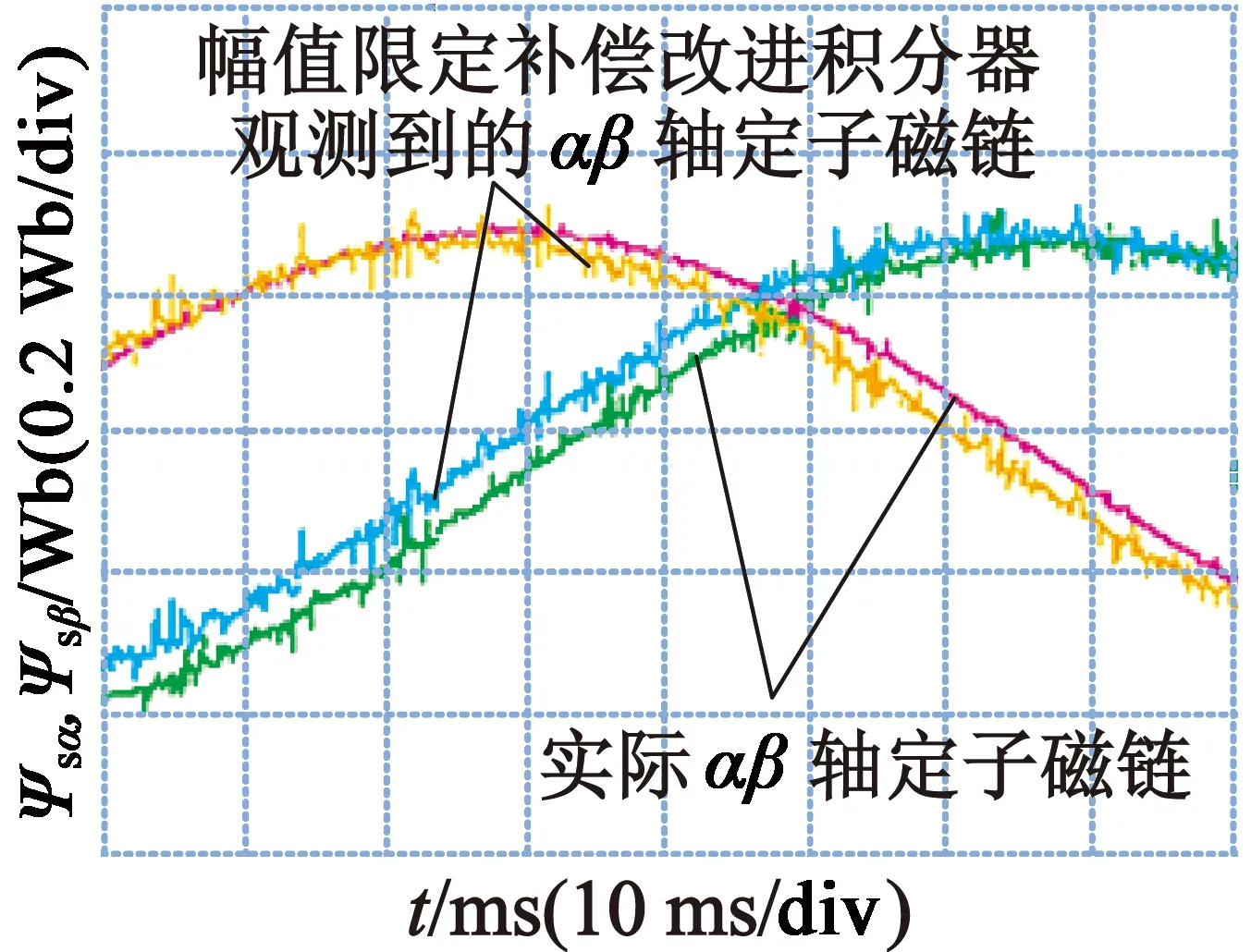
(b) 细节波形

如图10中标识所示得到的定子磁链分别为基于幅值限定补偿改进积分器的电压观测模型的结果以及电流观测模型观测到的近似实际结果。从实验波形可以看出，基于幅值限定补偿的改进积分器所观测到的定子磁链的幅值约为0.41 Wb，相比于给定定子磁链幅值0.43 Wb衰减了4.65 %左右，相比于一阶惯性滤波的积分方法幅值的衰减量减小了6.97 %，而该种积分方法观测到的定子磁链的相位前移了5 ms左右，结合此时的电压电流周期200 ms可知相位前移了9°，相比于一阶惯性滤波的积分方法相位前移量减小了13.5°。

表4 150 r/min转速下两种改进积分方法的性能对比

显然，低转速下一阶惯性滤波存在的幅值衰减和相位前移问题，利用幅值限定补偿的改进积分方法后，得到了较为有效的解决，体现出这种积分方法对定子磁链进行跟踪观测的有效性。

4 结 语

仿真分析和实验结果证明了相比于传统的纯积分器，一阶惯性滤波积分能够在永磁同步电机高速运行时有效抑制直流偏移量，而基于幅值限定补偿的改进积分方法则能够在更宽的转速范围中对传统纯积分器存在的直流偏移和易于饱和的问题进行有效的解决，所以通过对电压观测模型的积分方法进行改进之后能够显著改善定子磁链观测结果的精度。