基于LSTM网络的居民区供热负荷短时预测
2018-10-25许裕栗甘中学
许裕栗,姜 娜,陈 卓,李 柠,甘中学
(1.新奥科技发展有限公司,河北 廊坊 065001;2.煤基低碳能源国家重点实验室,河北 廊坊 065001;3.上海交通大学自动化系,上海 200240)
0 引言
近年来,随着监控、信息通信管理、新能源和互联网等技术的迅猛发展和广泛应用,以智能电网为核心的综合能源系统[1]得到了快速发展。以实现多能源开放互联、能量自由传输、能源绿色化、市场化及用能高效化为目标的“能源互联网”[2]概念应运而生,成为当前国际学术界和产业界关注的新焦点。用户侧供能负荷预测[3-4]作为能源互联网的关键技术之一,能够提高能源利用率,有助于实现错峰资源的分层优化与自动分配,从而实现能源生产与用能的协同调度[3],在能源互联网的运行管理中起着重要的作用。
目前,很多专家针对用户侧供能负荷预测问题进行了研究,常用方法分为基于统计的方法和基于人工智能的方法[1]。基于统计的负荷预测方法主要包括基于统计时序分析方法和回归模型方法[4-8],其通过分析历史负荷时序数据,定量地构建数学模型,对供能负荷进行预测。这类方法虽然原理简单,但不能处理负荷预测中的非线性问题,因而在相关变量较大变化时会产生较高的负荷预测误差。基于人工智能的方法是基于用户侧环境变量、占用设备以及历史负荷数据等信息,采用例如人工神经网络算法[9-10]、支持向量回归算法[11]等机器学习方法,建立供能负荷预测模型。该方法能够挖掘各变量之间的非线性关系,性能优于传统负荷预测方法,已成为近年来负荷预测领域的研究热点。但现有的基于人工智能的方法很少考虑数据内部的时序相关性。
针对上述问题,本文基于居民区的供热负荷历史数据,对居民区供热负荷短时预测进行了研究。通过引用深度学习算法中的一种能够学习时序数据长短期依赖信息的模型结构,即长短时记忆(long short-term memory,LSTM)网络模型[12],建立了基于 LSTM 网络的居民区供热负荷短时预测模型。
1 居民区供热负荷短时预测问题
居民区的供热负荷既与历史供热情况相关,又与当时外界气象环境的变化相关[9]。如果已知居民区历史供热数据和相关外界气象环境数据,就能够较为准确地预测未来的供热需求。居民区历史供热数据易于获取。但是受成本等因素的制约,外界气象环境数据较难获取,对准确预测供热需求造成了阻碍。通常情况下,居民区的供热情况是以时序数据的形式记录的。这些时序数据既反映了居民供热需求的变化趋势,又反映了一些与之相关的潜在特征变化情况,如随时间变化的外界环境情况。如果能够建立一个可挖掘数据潜在的特征及其内部随时间变化关系的模型,那就可以在只有历史供热数据的情况下,更准确地预测未来供热负荷。所以本文将居民区供热负荷短时预测的问题,转化为基于时序数据的回归问题:根据居民区供热负荷的历史数据,预测未来某一时刻或者某一时间段的供热负荷。LSTM网络作为深度学习循环神经网络模型的一个分支,能够记忆长期时间序列数据所包含的信息,捕捉时间序列之间的内在联系。因此,本文基于历史供热数据,挖掘居民区供热负荷的行为规律,根据LSTM网络模型学习居民供热负荷在时间维度上的内在联系,通过增加数据特征的维度提取原始数据中潜在的特征信息,对未来居民区供热负荷进行短时预测。
2 居民区供热负荷短时预测模型建立
2.1 LSTM 单元
LSTM是由 Sepp Hochreiter和 Jürgen Schmidhuber在1997年[12]提出的一种特殊循环神经网络。与传统循环神经网络模型相同,它也是基于时序数据,通过神经元之间的循环连接,挖掘时序数据间的内在联系,对时序数据进行建模。但与传统循环神经网络模型不同的是,它有一种被称为“记忆单元”的特殊神经元结构。通过该结构所构建的LSTM网络的隐层,能够存储任意时间长度的信息,获得更为精确的时间序列模型。
LSTM网络的记忆单元结构如图1所示。图1中:实线为网络单元件必须连接的结构;虚线为可选择连接的结构。

图1 记忆单元结构图Fig.1 Memory cell structure diagram
记忆单元模块由输入门、遗忘门和输出门这3个“门”结构和1个循环连接单元组成。其核心思想是通过非线性函数来控制各个“门”的开关,以保护和控制记忆单元的状态,从而控制信息的增减。因此,LSTM网络的关键就是通过记忆单元的状态长期存储数据的信息。一般情况下,3个“门”通过sigmoid函数来输出0~1的数值,从而决定有多少信息能够输入给记忆单元。
假设在t时刻,某记忆单元模块的输入为xt、输出为ht、单元状态为Ct,那么该记忆单元模块的输入门、遗忘门、输出门、输入转换、单元状态更新、隐层输出公式分别如式(1)~式(6)所示。
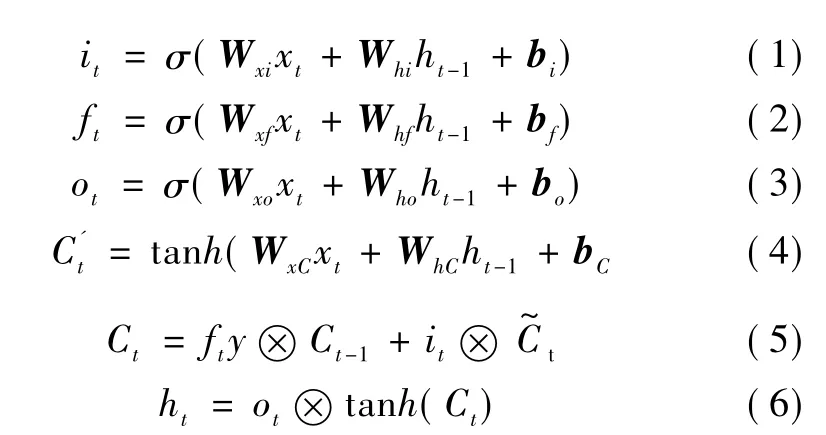
式中:σ为sigmoid函数;tanh为双曲正切函数;it、ft、ot和C't分别为输入门、遗忘门、输出门和输入转换对单元的输入;Wxi、Wxf、Wxo、WxC和 Whi、Whf、Who、WhC分别为与xt和ht-1对应的输入门、遗忘门、输出门和输入转换的权重矩阵;bi、bf、bo和bC分别输入门、遗忘门、输出门和输入转换的偏移向量。
输入转换根据xt和ht-1,通过tanh函数产生新的信息量;输入门读取 xt和 ht-1,并通过 sigmoid函数输出0到1的值(0代表不许任何信息通过,1代表允许所有信息通过);将其与信息量相乘,决定有多少新的数据信息能输入给记忆单元。同时,遗忘门读取xt和ht-1的数值,通过 sigmoid函数输出0~1的值(0代表完全舍弃,1代表全部保留),并将其与记忆单元上一时刻状态Ct-1相乘,以决定记忆单元中原始信息的保留与舍弃。然后,将新的信息与保留的原始信息相加,以更新当前记忆单元的状态为Ct。最后,输出门读取xt和ht-1的数值,通过sigmoid函数运算,并与通过tanh函数处理的记忆单元状态Ct相乘,从而决定记忆单元状态的输出信息。
2.2 LSTM 网络
LSTM网络是一种特殊的循环神经网络。由2.1节可知,其神经元通过比传统循环神经网络神经元增加1个单元状态,用来保存长期信息,解决了传统循环网络在训练中梯度消失或爆炸的问题。因此,LSTM网络的结构与传统循环神经网络的结构相同,均由输入层、隐层和输出层组成。隐层结构中增加了从上一时刻隐层到下一时刻隐层的连接,按时间展开的单层LSTM网络展开结构如图2所示。LSTM网络通过2.1节中所述的长短时记忆单元的计算过程,基于输入序列[x1,x2,…,xt],得到1 个隐层输出序列[h1,h2,…,ht]。通过对该序列进行某特定运算得到h,并对h进行预测或分类。

图2 单层LSTM网络展开结构图Fig.2 Single layer LSTM network unfolded structure diagram
2.3 短时预测模型整体架构
本文基于居民区历史供热热量数据,采用LSTM网络模型,构建了供热负荷短时预测模型。基于LSTM网络的居民区供热负荷短时预测模型如图3所示。
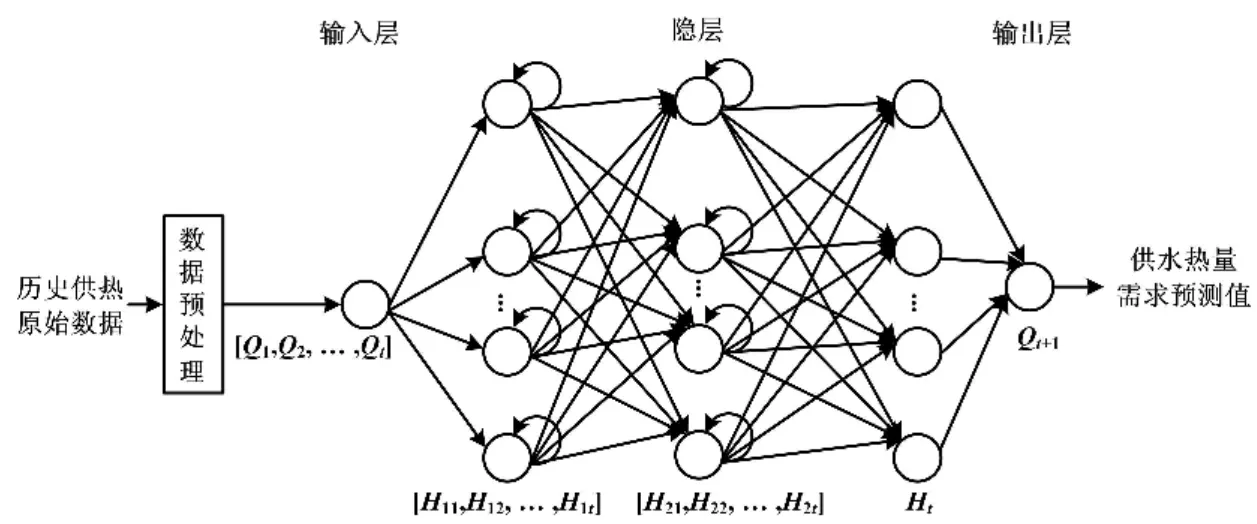
图3 供热负荷短时预测模型Fig.3 Short-term prediction model of heating load
①数据预处理。将噪声、采样间隔不一致的原始供水热量瞬时数据,转化为采样间隔时间在k min内的累积供水热量标准化数据,其大小为n×m。其中:n为数据集含有的天数;m为日累积供水热量序列长度。
由于数据的每一行代表以k min为采样间隔的每天的累积供水热量序列,故
②数据集输入/输出的构建。本文以天为周期,选前t个时刻的时间序列数据作为样本输入,第(t+1)个时刻的数据为该样本的输出。依次顺延,则1天内的样本个数为(m-t),输入样本大小为(m-t)×t×1,输出样本大小为(m-t)×1。由此可知,本文输入数据为[n(m-t)]×t×1的3维数组,输出数据为n(m-t)维的向量。
③基于LSTM网络的预测模型构建。由图3可知,该网络包含1个输入层、l个隐层和1个输出层。输入层神经元个数为输入数据所含的特征数。本文只选用前t个时刻的历史数据序列作为输入,因此所构建的预测模型输入层为单输入层。隐层为LSTM层,前(l-1)个LSTM层的神经元均输出长度为t的序列[Hi1,Hi2,…,Hit],作为下一层的输入;最后 1 个 LSTM层选取第t个时刻的输出Hlt,作为输出层的输入。输出层为预测回归层。其神经元个数为所需预测的未来时间段累积供水热量个数。本文只预测第(t+1)个时刻的累积供水热量。因此,本文构建的预测模型输出层为单输出层。
④未来时刻供热负荷预测。本文将前t个时刻的累积供水热量序列数据作为输入,采用LSTM网络,预测第(t+1)个时刻内居民区累积供水热量。假设Q(t+1)为第(t+1)个时刻内居民区累积供水热量,则 Q(t+1)=G[Q(t),Q(t-1),Q(t-2),…,Q(1)]。其中:G为已经训练好的预测模型。
3 试验及结果分析
3.1 试验数据描述与预处理
对山东某工业园居民区2016年11月~2017年2月冬季供暖时间段所记录、存储的供水热量表瞬时数据进行研究。该工业园居民区UIQ_201住宅供水热量如表1所示。

表1 住宅供水热量表Tab.1 Heat meter of residential water supply
由表1可知,原始供水热量数据采样时间间隔并不统一,不能直接用于预测模型训练。因此,首先要对原始数据进行预处理,将其转化为采样时间间隔一致、能直接用于模型训练的标准化数据,具体过程如下。
①分钟级数据滤波降噪。采用中值平均滤波算法,对1 min以内的数据进行降噪平滑处理。即对于1 min以内的序列数据,去除其中的最大值与最小值后取平均值,作为该时间内的平均供水热量数据。例如2016年11月26日17∶00~17∶01内的数据序列,对其进行中值平均滤波,去除其中的最大值8 935.13和最小值8 502.83后,其均值为8 654.39。设定该值为该时间段内的平均供水热量数据。通过该步骤,把原始数据转换为采样间隔为1 min的平均供水热量数据。
②累积供水热量数据转换。为了更好地适应实际场景的需求,将滤波后采样间隔为1 min的平均供水热量数据转换为采样时间间隔为k min的累积供水热量数据。例如:t时刻的累积供水热量为Q(t),则其中:q(i)为第i min的平均供水热量。
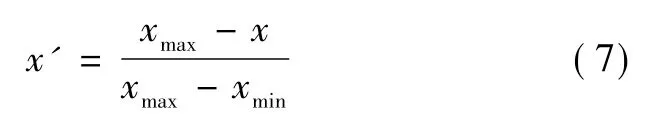
3.2 试验过程与结果分析
本文选用均方误差(mean square error,MSE)作为模型训练时使用的损失函数,选用平均绝对百分比误差(mean absolute percent error,MAPE)作为预测模型的评估准则。其定义如式(8)~式(9)所示。
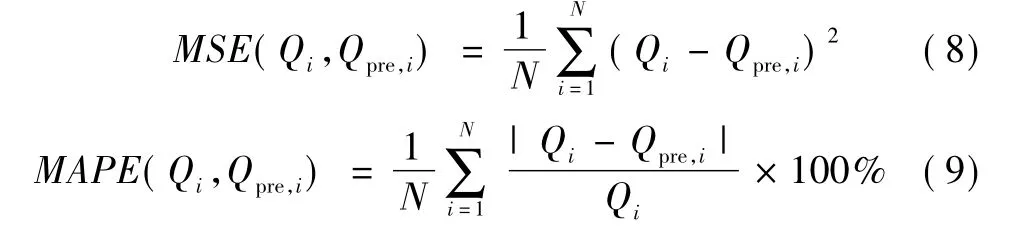
③数据集分割。本文采用的数据集共有107 d供水热量表瞬时热量数据。随机选取82 d数据作为训练集,14 d数据作为验证集,11 d数据作为测试集。
④数据归一化。为了更好地进行模型训练,需要对数据集进行归一化。本文基于式(7)对数据进行最大最小值归一化,将其转换为[0,1]的值。
式中:N为测试样本个数;Qi为第i个样本的实际输出值;Qpre,i为第i个样本的预测输出值。
本文基于keras深度学习架构搭建LSTM网络,构建基于LSTM网络的供能需求预测模型。选用随机梯度扩展式优化算法训练LSTM网络,用于得到较优的预测模型参数。
试验中,设定时间间隔k为1 h。首先,对输入数据样本的序列长度t进行选择。选取网络隐层层数为2 层,每层神经元数为50,t从{2,3,4,5}中分别选取,时序长度t-MAPE选择试验结果如表2所示。
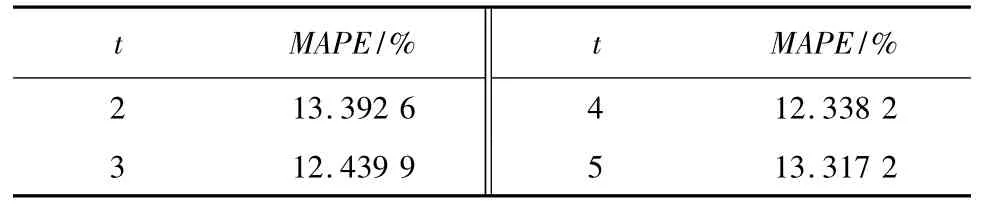
表2 t-MAPE选择试验结果Tab.2 Results of t-MAPE selection test
由表2可以看出,随着t的增加,预测模型在测试集上的MAPE先减小后增大,在t=4时模型的预测精度最高、性能最好。试验表明,当时序长度t=4时,前4 h的数据与后1 h的供热负荷联系紧密。因此,后续试验选取时序长度t=4。
LSTM网络的隐层层数和神经元数对于网络的训练起着关键性作用。网络的隐层层数和神经元数越多,网络越复杂,预测模型的训练精度越高;但随之会出现过拟合的现象。为了获得精度更高、泛化能力更好的预测模型,同时避免预测模型过拟合的问题,需要对网络的隐层层数和神经元数进行选择,从而得到较优的LSTM网络,用于预测模型的训练。本文采用网格搜索法,对隐层层数和神经元数进行选择。其中,隐层层数在{1,2,3}中变化,每层神经元数在{20,30,40,50,60}中变化。随着训练迭代次数的增加,模型的MSE均逐渐减小至趋于收敛,在隐层层数为1、神经元数为30时,MSE取得最小值,同时训练集和验证集的拟合程度均达到最优。隐层层数 Nk/神经元数Nn-MAPE选择试验结果如表3所示。

表3 Nk/Nn-MAPE选择试验结果Tab.3 Results of Nk/Nn-MAPE selection test %
由表3可知,随着神经元数的增加,测试集的MAPE先减小后增大。分别在隐层层数为1、神经元数为30,隐层层数为2、神经元数为50,隐层层数为3、神经元数为40时,取不同隐层层数在测试集上的最小MAPE。此外,随着隐层层数的增加,测试集的MAPE逐渐增大,这说明解决本文中的问题只需一层LSTM网络就足够了。层数的增加会导致模型的复杂化,从而出现过拟合的现象。综合试验结果可知,模型在取隐层层数为3、神经元数为4时MAPE最小,预测性能最优。
最终确定本文中基于LSTM网络的居民区供热负荷预测模型的隐层结构为单层LSTM网络,其中神经元数为30。经过测试,本文提出的基于LSTM网络的居民供热负荷短时预测模型对未来供热负荷预测MAPE 为12.781 6%。
将该模型与自回归积分滑动平均模型(autoregressive integrated moving average,ARIMA)预测模型、反向传播(back propayration,BP)神经网络预测模型和支持向量回归(support vector regression,SVR)预测模型这3种传统数据驱动模型进行对比。其中,传统数据驱动模型输入数据为由相同历史数据集生成的二维数组,则各预测模型对比试验结果如表4所示。
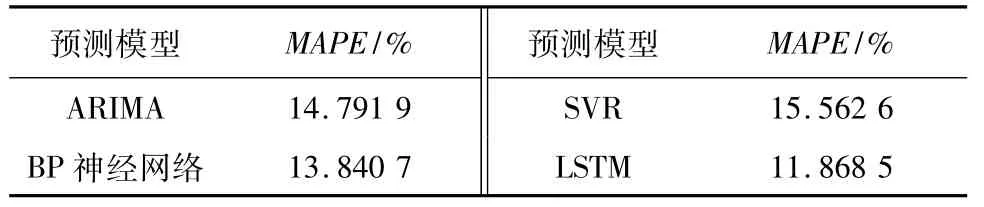
表4 各预测模型对比试验结果Tab.4 Experimental results of comparison among different prediction models
由表4可知,相较于传统的供热负荷预测模型,基于LSTM网络的供热需求预测模型有更高的精度。其精度比ARIMA预测模型高19.76%,比BP神经网络预测模型高14.25%,比SVR预测模型高23.74%。试验结果表明,相较于传统预测模型,基于LSTM网络的模型能更全面地学习时序数据间内在的联系,更好地提取隐藏在数据中潜在的特征知识,从而基于历史供热负荷数据,更准确地对未来的供热负荷进行短时预测。
4 结束语
由于LSTM网络具有学习时序数据长短期依赖信息的特点,本文将其引入居民区供热需求短时预测问题中,建立了一种基于LSTM网络的居民区供热需求短时预测模型。通过学习前t个时间段历史供热时序数据的潜在特征与规律,训练合适的LSTM网络回归模型,以预测下一时间段内的供水热量需求。试验结果表明,与传统供热需求短预测模型相比,基于LSTM网络的预测模型显著提高了供热需求预测的精度。
在未来研究中,将扩大数据集规模,引入与供热负荷相关的气象数据,构建基于LSTM网络的多步预测模型与供热需求长时预测模型。
