RFID系统射频电路优化设计研究

王 烁

（天津科畅慧通信息技术有限公司，天津 300000）

RFID系统由于操作的便捷性已经在多种行业中得到应用，常见的如零售业、交通运输业、生产流水线和防伪技术等都可应用RFID技术。为了提升RFID系统的性能，本文根据先局部后整体的优化思路进行电路优化，并在电路优化完成后对电路进行测试，将优化结果与设计值进行比较，从而实现对RFID系统射频电路的优化设计。

1 RFID系统原理

RFID系统主要由读写器、控制装置和标签构成。读写器包括天线、射频电路和数字电路。控制装置通常为计算机。标签包括存储器、天线和收发机。

RFID系统中的标签为数据载体，标签中包括多种电子器件和线路，最终使标签具有唯一的数字编码。当标签附着在物体上时，通过读写器能够得到标签中的唯一编码，经过解调可以将编码进行显示或处理。标签按照有无独立电源供电可分为有源标签和无源标签，当前无源标签使用范围更加宽泛，而要让标签中的电子器件运行，读写器中的天线能够为标签提供能量，从而激活标签中的电子芯片[1]。

RFID系统中读写器是通过天线进行信号的发送和接收，从而获取标签内的编码，对于一些拥有写入功能的读写器，还可以对标签中的编码进行修改。通常情况下，读写器都有数据连接插口，以将得到的数据传输到相应的控制装置中。另外，对于RFID系统来说，高频信号和低频信号在电路设计中存在较大差异。以高频系统为例，电路设计中涉及防碰撞技术、零中频技术、天线技术等方面。

2 RFID系统射频电路设计

2.1 发射电路设计

发射电路设计中包括调制器、耦合器、电源电路、频率源和功率放大器电路设计，各电路设计方案如下：（1）频率源。频率源设计需要通过频率合成实现，频率合成有直接合成和间接合成两种方式。从成本、信号质量方面考虑，最终决定使用间接合成方式。使用锁相环可以实现频率的间接合成。锁相环的工作原理为一个反馈电路，通过误差控制电压实现对频率的有效调整，并且在该系统中还设置了环路滤波器，进一步提升输出信号的品质。（2）调制器。根据相关协议，需要保证前向链路的调制系数高于90%，同时波形动作时间不能高于35 μs，最终确定采用具有开关功能的功率放大器替代调制器，在放大信号的同时还能够进行ASK调制[2]。（3）功率放大器。功率放大器设计中需要按照信号发射最远距离进行设计，同时需要对放大器的体积进行合理选择。（4）耦合器。耦合器的作用是当发射器中只有一个发射天线时，对发射信号和接收信号进行隔离，对于高频信号来说，耦合器可使用微带线实现功能。（5）电源电路。在电源电路设计中，为了保证发射信号质量，需要在线路中增加滤波电路，同时还需要增设稳压管保证电源电压的稳定性。

2.2 接收电路设计

接收电路为RFID系统线路设计的重点和难点，在接收电路设计中，需要对电路的解调原理、模糊点处理进行研究。另外接收电路设计时，在同一条微带线上需要连接4个混频二极管。本振信号和标签回波信号经过其中两个二极管形成的混频电路，进行信号处理后，将信号输入差分放大器，最终流经电压比较器[3]。

2.2.1 解调原理

在本振信号和回收信号流经一个混频电路时，两个二极管上得到的信号分别为：

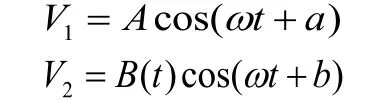
在这两个方程中，A为信号强度，B(t)为调制信号，在信号解调过程中，需要保证，当这两个信号在流经其中一个点处发生混频后，最终输出的信号会包括直流成分、零中频成分、基波成分和高频谐波成分。其中，零中频成分由两个信号的差频产生，信号方程为：

该方程中c为一个常数，需要根据二极管确定，在进行信号处理时，需要将直流成分、基波成分和高频谐波成分去除，得到的信号即为基带信号。构建两个二极管间距为微带线长度的1/4，则可将本振信号和回波信号写成：

在该方程中，e为常数，与二极管自身性质有关。对得到的两个信号方程比较可知，两个信号方程互为倒相，且这两个信号都为解调信号。对这两个信号进行放大后，让信号通过电压比较器即可得到解调信号。

2.2.2 模糊点

通过得到的解调信号方程可以发现，当a－b=0.5 π时解调信号输出值为0，而a－b的值由读写器与标签间的距离决

与之前的分析过程相似，最终得到另一点的输出信号为：定，在RFID系统中将距离为0.5 π的位置称为模糊点。在电路设计中，可以将本振信号与回波信号的相位设置为任意值，并按照上文的解调方法对信号方程进行处理，对于同一组二极管，将两个解调信号相减，得到方程：

其中δ在确定的电路中为一个固定常数，另外通过上述方程可以找到方程的模糊点，要消除电路中模糊点对RFID系统的影响，需要在电路中增加解调电路，以消除电路中产生的模糊点，并且在该过程中需要确定增加的解调电路的位置，以解调电路中两个二极管距离为微带线长度的1/4为例，最终结果为：新增的解调电路与原有解调电路间距要满足：，其中λ为微带线长度。

3 RFID系统射频电路优化

3.1 混频器优化

在RFID系统中，混频器发挥重要作用，所以需要对混频器进行优化，在实际电路构建时，通常在混频二极管与微带线间设置电容。这种结构能够防止微带线中的直流电流通过二极管，对信号产生一定影响。同时通过设置电容，也能保证读写器中发射信号的强度。对于混频器中二极管的选择原则为截止频率不低于本振频率的10倍，并且与之串联的电阻需要保证低阻。其中电容的确定公式为：

该方程中，f为截止频率，R为与二极管串联的电阻阻值，在根据该公式选取相应的电子元件后，通过建模仿真的方式对电路进行测试。结果表明，本振频率不会对混频器的变频增益产生重大影响，而电容的加入会对变频增益产生较大影响，并且通过建模仿真过程还可以找到变频增益最大时对应的电容值。另外，增加电容后，微带线的本振信号和回波信号衰减值会大幅下降，表明本振信号能够被很好地利用。

3.2 混频管间距优化

通过前文可以发现，混频器中二极管的间距会对信号的接收造成较大影响。为了能够充分提升信号的强度，需要对二极管的间距进行优化设计。要达到这一目的，需要保证差模信号幅度获得充分提升，即求的最大值。由于该方程中a，b，δ为已知常数，故而只需要求取方程右端前半段的最大值即可，其中c，h为绝对值相同的已知常数。通过对方程最大值的求解，可以发现，当方程中时，方程将取得最大值。体现在RFID系统的电路中，即混频二极管间距为微带线长度的1/4时，取得最大的差模信号幅度。

3.3 带通滤波器优化

带通滤波器的最终目的是得到较为纯净的零中频信号，在带通滤波器优化过程中，首先需要计算零中频码的频谱，其次设计相应的电路实现所需功能。在带通滤波器优化过程中，使用时域仿真器进行时域信号的傅里叶变换，得到的结果表明，频谱虽然无限长，但功率集中在1 MHz范围内，在32 kHz左右功率达到最大，所以在带通滤波器优化中，应保证滤波器通带处于20 kHz～1 MHz范围之内。在进行滤波电路设计时，需要尽量降低滤波电路的体积，同时还要考虑不同电路的制造成本。在进行电路设计和构建后对最终结果进行测试，结果表明优化后的带通滤波器能够充分发挥应有作用。

3.4 工作频率优化

在读写器使用过程中，手机与读写器的工作频段存在重叠部分，这会产生同频干扰，所以需要对工作频率进行优化，降低干扰现象的发生概率。工作频率优化中最主要的方式为跳频优化方式。这种优化方式的原理是将读写器的工作频率进行定期随机改变，而且由于标签的能量来源为读写器，所以在采用跳频优化方式时，不需要对标签部分进行重新设计。另外对于同一区域内有多个读写器运行的情况，需要通过控制系统将读写器的工作频率进行合理划分，并使读写器在相应的频段范围内跳频，避免同频干扰现象的发生。

3.5 模糊点消除

通过电路设计过程可以发现，当RFID系统中只存在一个解调器时，系统运行中会生成模糊点，影响设备使用，所以需要在电路中设置另一个解调器，以消除模糊点，设计的最终目的为确定微带线上两个解调器间距。本文设计的电路中，解调器的两个二极管间距为微带线长度的1/4，在此基础上计算得到，要对模糊点进行消除，两个解调器间距应满足条件：

通过对构建电路的建模仿真可以发现，当电路中的两个解调器符合计算该间距要求时，读写器使用过程中将不会出现模糊点。

4 结语

综上所述，RFID系统电路设计中，需要对读写器和标签系统进行重点设计，其中读写器电路设计较为复杂，需要在了解相关原理的情况下设计。电路优化过程中，将主要对混频器电路、混频管间距、带通滤波器和工作频率进行优化。同时，在接收电路设计中，通过解调电路间距的合理设计会消除模糊点，保证RFID系统的正常稳定运行。