含平衡机约束条件的区间直流潮流模型与方法
2018-10-24鲁广明严剑峰李方兴毛学魁
鲁广明, 严剑峰, 丁 涛, 谢 昶, 李方兴, 吕 颖, 毛学魁
(1. 中国电力科学研究院有限公司, 北京市 100192; 2. 西安交通大学电气工程学院, 陕西省西安市 710049;3. 电力系统及发电设备控制和仿真国家重点实验室, 清华大学, 北京市 100084;4. 田纳西大学电气工程与计算机科学系, Knoxville, TN 37996-2100, 美国; 5. 国网北京海淀供电公司, 北京市 100195)
0 引言
潮流计算是电力系统能量管理系统重要组成部分,为调度运行人员提供了重要的指导。根据潮流方程的形式,潮流计算的模型主要分为交流潮流和直流潮流。其中,直流潮流是交流潮流的近似,在电力市场分析中广泛应用,能够快速评估输电系统的潮流状态。然而,电力系统通常处在不确定的运行环境中,特别是当大规模可再生能源接入电网时,其随机性给传统电力系统分析和计算带来新的挑战。如何快速准确获取电力系统随机状态,分析不确定功率注入下的输电系统波动范围,并发现潜在的传输不安全是当下研究的热点和难点[1-3]。为解决随机功率注入下的不确定潮流问题,首先必须对不确定量进行合理有效建模。根据不同建模方式,可将不确定潮流计算分为模糊潮流[4]、概率潮流[5-9]和区间潮流[10-15]。
模糊潮流采用模糊数建模方式,并按照模糊数定义的运算法则进行计算[4]。概率潮流则是通过历史数据得到不确定能源出力的概率分布,通常采用半不变量法来代替卷积运算得到系统潮流的概率分布[8],区间潮流则以区间方式建模,并且只关心不确定量的边界信息,能够得到直观的信息,因此得到了广泛的研究。
文献[10]采用仿射与区间相互转换并迭代运算,在一定程度上克服了区间运算的保守性。文献[11]利用切比雪夫误差估计,建立仿射优化模型来求解区间潮流;文献[12]建立了非线性优化模型来求解交流区间潮流。相比区间交流潮流,区间直流潮流方程具有较好的线性特性,由此产生了基于高斯消去法[13]、Krawczyk迭代算法[14]以及区间Hull算法[15]的求解方法,并被证明具有很好收敛效果。
然而,区间运算存在一定的保守性[11-13],这使得区间计算结果越来越保守,区间运算的保守性是影响其应用的重要原因。基于已有文献来看,大多数采用仿射或者优化方法来克服,但对于高维复杂问题,仿射运算需要通过迭代的方法对仿射展开式和区间数进行等价转换,并且仿射方法需要得到准确的仿射展开式,否则相关性不能完全被消除。文献[16]进而提出一种仿射非迭代的区间潮流求解方法,将仿射展开采用优化方法进行求解,得到了较好的结果。
另一方面,电力系统实际运行中需要考虑特定的物理约束,如发电机出力限值、潮流准稳态调整等,从而形成了含约束的区间潮流问题。以往文献中尚未考虑这些物理限值,因此得到的区间结果较为保守,甚至部分区间取值没有实际物理意义。为此,文中提出了含约束的区间直流潮流模型,分别以平衡机出力约束和发电准稳态调整约束为例进行建模分析,可以看出,含约束区间直流潮流得到的结果更符合实际的物理含义,并在一定程度上克服了保守性。
需要说明的是,本文的研究主要涉及不确定注入对传输系统的影响,因此采用直流潮流进行分析。事实上,本文基于优化的含约束区间潮流建模和求解方法可以扩展应用到交流潮流方程上,只需将模型中的直流潮流方程替换成交流潮流方程。
1 区间算术运算保守性分析
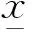
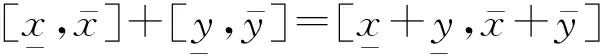
(1)
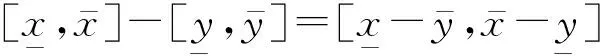
(2)
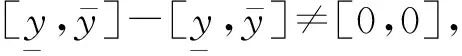
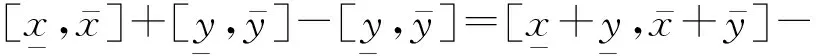
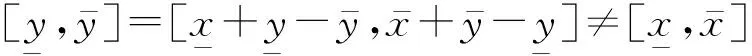
(3)
为此,文献[10]提出了一种仿射求解的方法,由于仿射数学满足线性映射的基本性质,因此能够较好处理的基本思路是将相关的变量用相互独立的噪声元展开,进而克服区间运算的保守型。针对上述例子,由式(4)和式(5)可知,仿射计算能够得到正确的计算结果[0,0]。
(4)
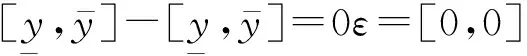
(5)
但仿射方法需要得到精确的仿射展开式,并且计算相对区间要复杂得多,在非线性情况下,处理的难度更大。特别的,区间潮流如果考虑一些物理约束后,将不再是传统的区间线性方程组或者区间非线性方程组,而是包含了等式和不等式的约束方程组。此时,含约束的区间潮流问题在数学上将对应为一个约束满足问题(constraint satisfaction problem,CSP)。传统求解区间线性方程组和区间非线性方程组的方法,如仿射运算,将无法试用。
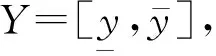
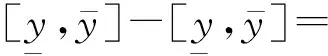
(6)
2 含平衡机约束的区间直流潮流建模
2.1 区间直流潮流模型
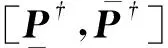
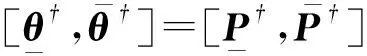
(7)
(8)
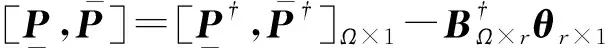

(9)
(10)
(11)
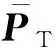
由于电力系统需满足实时的电力平衡,则节点注入功率和为0,因此平衡节点功率可由式(11)得到。
2.2 含平衡机约束的区间直流潮流
在给定的节点注入的区间表达后,根据矩阵运算,可直接由式(10)得到支路功率的区间范围。事实上,在式(9)和式(10)描述的区间直流潮流中,负荷(或者可再生能源)的功率都是在给定的区间内任意取值的。但实际传统电网中,负荷可以作为不可控随机变量,在不确定区间内任意取值,而发电出力为可控变量,往往受到某些物理限值,不会任意波动。这些额外的等式或不等式约束结合式(9)和式(10)定义的区间直流潮流方程构成含约束的区间直流潮流方程。
系统不确定性必然导致发电机的出力也相应地在一定区间范围内波动。但由于考虑发电机的实际约束存在,使得相应的区间潮流结果与传统不考虑约束的区间潮流结果发生改变,而这个结果要比传统不考虑约束的区间潮流结果更符合实际的物理特性。进一步,将区间直流潮流方程分为负荷和发电两部分,得到式(12),其中负荷作为自由变量,可在区间内任意变化,而发电机出力为可控变量,但需满足一些约束条件。相应的,平衡节点的出力可描述为式(13)。
(12)
(13)
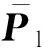
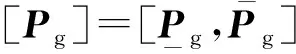
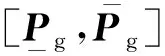
(14)
根据不同的约束限制,下文中将给出两种含约束的区间直流潮流表示形式。
1)含平衡机出力约束
与传统潮流计算类似,对于式(9)和式(10)定义的区间直流潮流方程,平衡节点并不参与计算,而在最后通过平衡系统功率而得到。从另一个角度分析,网络中的不确定量相当于全部由平衡节点承担,但平衡节点出力具有发电出力上下界的约束,并不是无约束的,因此需要将平衡节点的出力显示表达出来,并满足式(15)。即将式(13)代入式(15),可得到式(16)。
(15)
(16)

针对支路的传输功率,由式(10)和式(16)构成带约束的区间直流潮流方程如下:
(17)
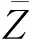
(18)
(19)
2)含平衡机约束的准稳态区间潮流
不难看出,模型1中考虑系统的不平衡量由平衡节点承担。而在电力系统实时运行时,不平衡功率实际上是由所有发电机共同承担的,从而形成了准稳态潮流[17]。一般而言,发电机出力是可控的,其出力的动态变化是为了满足实时功率平衡,因此在考虑负荷变化为区间的情况下,发电的出力也为区间表达,便构成了准稳态区间潮流。此时,若考虑第i台发电机分担网络不平衡功率的权重为αi,那么,在此种情况下,区间潮流则在式(12)的定义下,增加了一系列的等式约束,进而表示为:
(20)
(21)
当然,含平衡机约束的区间潮流并不仅限以上两种情况,根据实际电力系统运行条件和物理约束,均可在原始区间直流潮流的基础上增加一系列有意义的约束,构成含约束的区间直流潮流,进而转化为优化模型进行求解。
最后,针对所提出的两种含约束的区间潮流模型,模型1和模型2均为线性优化模型,可采用基于CPLEX软件中的单纯形法快速求解。
3 算例仿真分析
3.1 传统区间潮流与平衡节点约束的区间潮流对比
本文采用9节点系统[18]对所提方法进行测试,其中该系统共有3个负荷、3台发电机以及9条线路。其中,节点1的发电机为平衡机,节点2和3的发电机为PV节点。考虑各个负荷节点的注入功率在±30%内随机变化,而平衡机出力限制在其出力的上下界,即[50,150]MW。传统区间潮流可采用文献[15]的方法求解。
比较传统区间潮流和模型1中定义的含约束区间潮流,结果如表1所示。可以看出,含约束区间直流潮流结果为传统区间潮流的一个子集,这是因为在受到平衡节点功率约束后,发电机出力并不那么自由,受物理约束,使得实际传输功率区间减小。
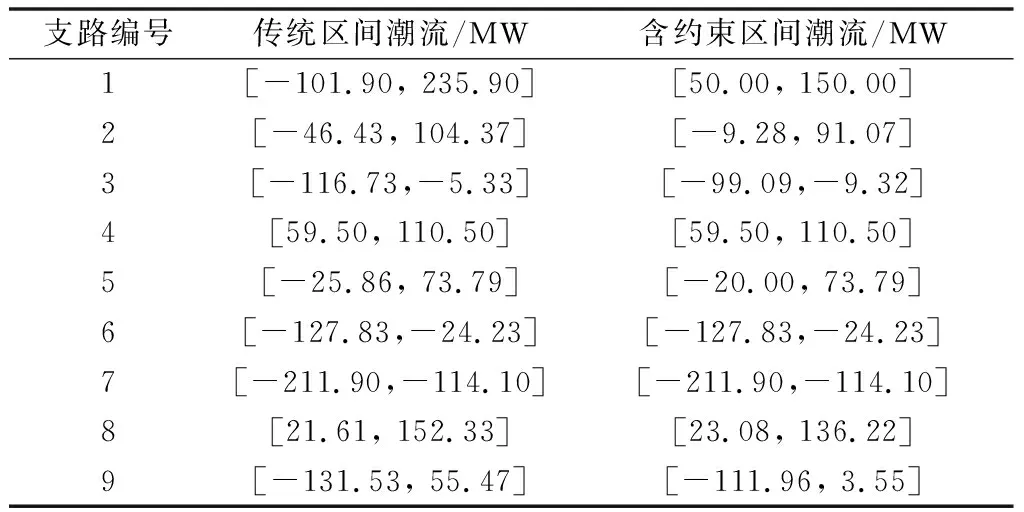
表1 传统区间潮流和含约束区间潮流的比较Table 1 Comparison of traditional interval power flow and constraints-included interval power flow
进一步考虑不确定对传统区间潮流和含约束区间潮流的影响,分别设置不确定量为±10%,±30%和±50%,其仿真结果如图1和图2所示。随着不确定量的增加,传统区间潮流和含约束区间潮流的区间功率宽度均呈现单调增加的趋势。但含约束的区间潮流的功率变化量并没有传统区间潮流那么大,这是由于考虑平衡机的功率约束,使得变量的自由度受到一定约束。另外,可以看出,1号线路(与平衡机直接相连)的区间功率明显受到了约束。此外,9号线路的功率变化也有所降低。
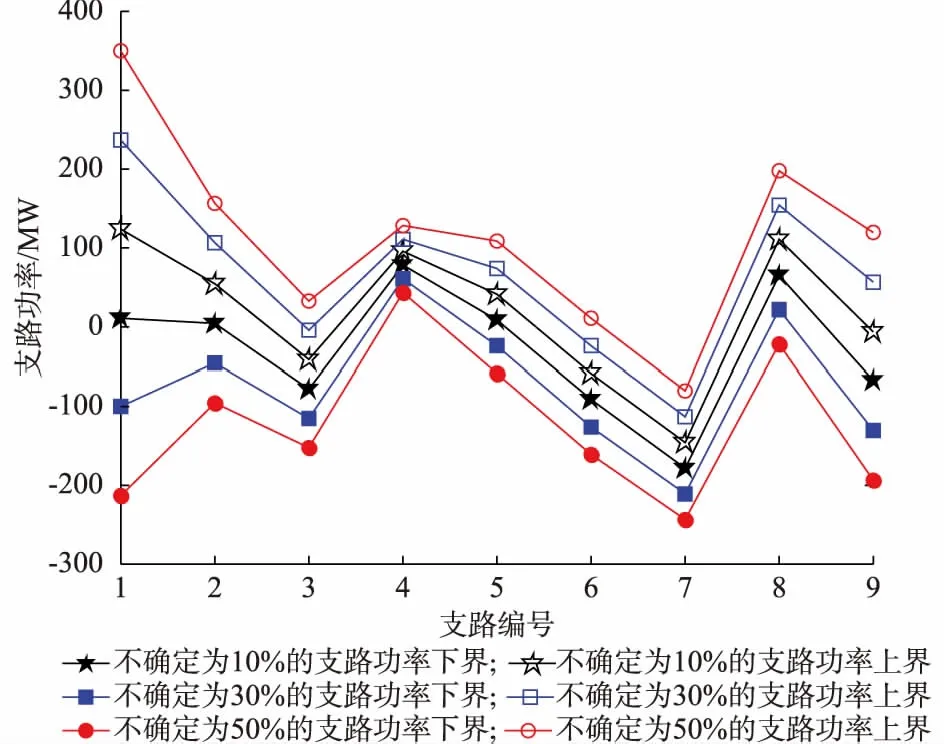
图1 不确定量对传统区间潮流的影响Fig.1 Impact of uncertainties on traditional interval power flow
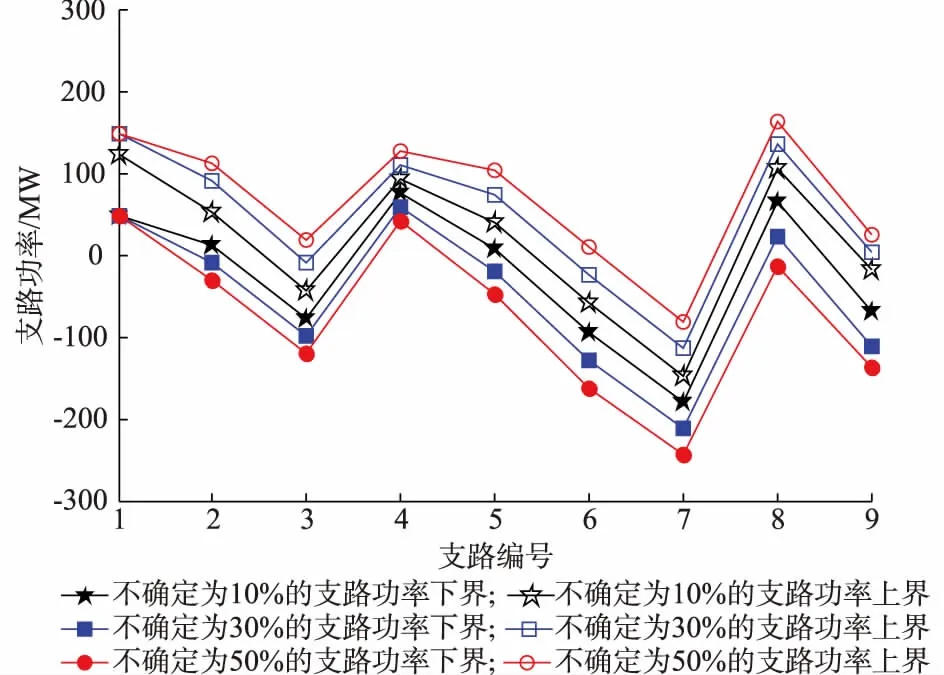
图2 不确定量对含约束区间潮流的影响Fig.2 Impact of uncertainties on constraints-included interval power flow
3.2 传统区间潮流与区间准稳态潮流对比
同理采用3.1节的仿真系统,考虑发电机等比例动态分配不平衡功率,利用式(21)的线性优化模型,得到在30%不确定下的区间准稳态潮流结果如表2所示。可以看出,所得到的区间准稳态潮流的区间范围相对更窄,由于所有发电机的出力需要动态分配,变化不会像前面几种情况那么自由,相当于受到的物理约束更强。如图3所示,随着不确定量的增加,区间准稳态潮流的区间宽度变化程度相对较小。
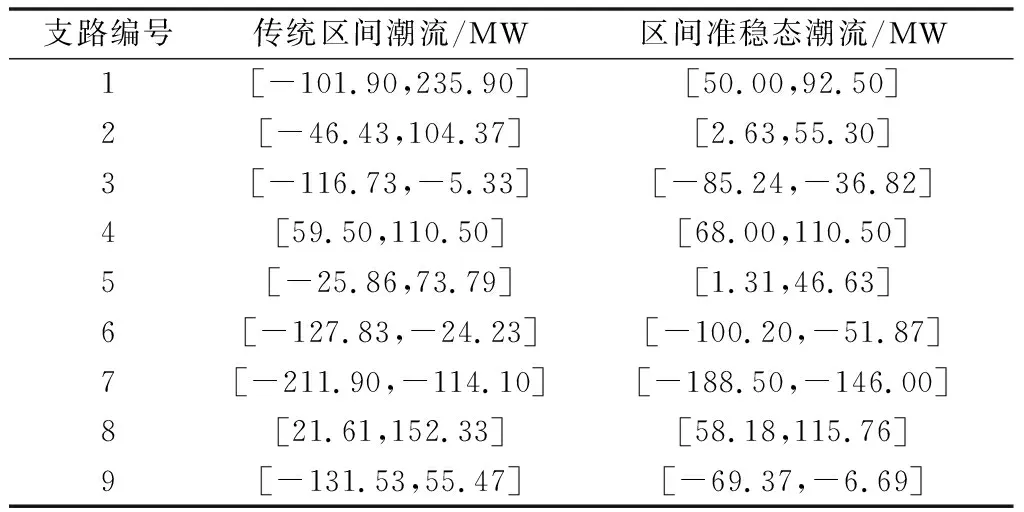
表2 传统区间潮流和区间准稳态潮流的比较Table 2 Comparison of traditional interval power flow and interval steady-state power flow
此外,9节点系统中发电机动态分配系数对区间准稳态潮流的影响,以及118节点的含约束区间潮流的仿真算例结果可见附录A。
4 结论
文中提出了一类含约束的区间直流潮流模型,在传统区间直流潮流基础上,分别对考虑平衡机出力上下界物理约束和发电机不平衡功率准稳态调整的两种情况进行详细建模,并化为相应的优化模型进行求解。采用9节点系统和IEEE 118标准节点系统算例对文中两种模型进行仿真测试,并与传统区间直流潮流进行对比,结果表明两种含约束区间潮流均能得到更优的区间结果,并且区间准稳态潮流结果最为紧致,含平衡机约束的区间潮流次之。最后需要说明的是,所提出的含约束的区间直流潮流模型并不局限文中所提出的两种模型,根据实际需要进行合理地建模,形成相应的约束条件,增加至区间直流潮流模型的约束条件中。
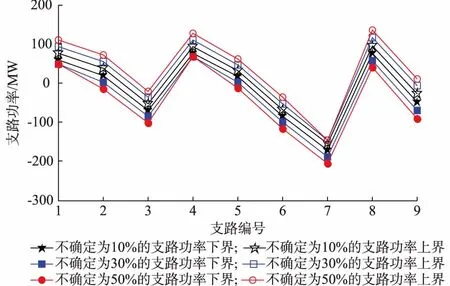
图3 不确定量对区间准稳态潮流的影响Fig.3 Impact of uncertainty on interval steady-state power flow
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。
