非负矩阵分解耦合视觉多样性的图像检索算法

仲宝才，张福泉，徐 琳

(1.成都东软学院 计算机科学与技术系，四川 成都 611844；2.北京理工大学 软件学院，北京 100081；3.福建师范大学 创新信息产业研究所，福建 仓山 350007)

0 引 言

基于内容的图像检索技术(CBIR)主要是通过计算查询图像和数据库特征之间的相似性来搜索目标图像[1,2]。尽管CBIR可基于视觉内容完成图像检索，但是由于视觉特征与语义属性间易出现语义鸿沟，使得CBIR系统不能通用化、高效化，且CBIR对于用户的习惯是不自然的[3]。

近年来，随着图像共享网站的发展，如Flickr、Picasa用户提供的标签，成为一种新的方式来描述图像的内容。与其它文本描述相比，标签能更准确、更有效地表示社交图像的视觉内容。因此，基于标签的图像检索(TBIR)能有效解决CBIR的不足[4]。如陈飞等[5]提出一种目标提取和哈希机制的标签图像检索方法。该方法提高了TBIR性能，但是其不能同时有效含有多个目标的复杂图像。因为对于含有多个目标的复杂图像时，只用一个哈希码不能准确描述每个目标，从而降低了检索精度。周燕等[6]设计了2D压缩感知与分层特征的图像检索技术。该方法对于简单点的图像能够有效检索，但对于较复杂的图像时，其检索精度不高，易出现语义鸿沟，且对参数较敏感。李军等[7]设计了一种视觉注意机制与CNN的图像检索方案。通过可变长度特征序列表示图像，通过CNN(convolutional neural network)提取底层特征作为序列模型；再利用中间层LSTM(long short-term memory)形成局部特征的相关性描述；其次，通过视觉注意LSTM得到向量表示图像；利用匈牙利算子测量图像相似度得到图像检索结果。该方法对多标签图像能较好提高检索性能。但对于图像标签不完整、模糊、含噪声时，易导致图像检索精度不高。

图像和标签之间的关系可以用标签图像矩阵表示，标签图像矩阵中的值为1或0，其对应的矩阵元素可以反映标签与图像间的相关性。因此，本文利用图像标签，提出了非负矩阵分解耦合视觉多样性的图像检索算法。通过NMF对低秩空间中发现标签的相关性，最后根据分解因子的乘积来完成缺失标签的重构，得到标签图像矩阵。并在NMF过程中嵌入了整体视觉多样性，利用最小化图像之间的总平方差和标签来减少标签的整体视觉多样性。然后，为保证标签图像矩阵的正确校正和稀疏性，引入两个正则化因子对其进一步优化，将两个正则化因子与NMF、整体多样性相结合，并控制优化框架的复杂性。最后，通过计算图像矩阵的标签语义距离进行相似度量，完成图像检索。提出方法的主要贡献如下：

(1)NMF用于发现标签之间的语义相关性，并完成标签之间的缺失关系，其中NMF可以将标签投射到潜在的低秩空间，并推断标签之间的缺失关系。

(2)提出了标签的整体视觉多样性，并通过图像与标签特定手段的差异来衡量。

(3)为了防止过度计算，采用微分和稀疏项来控制提出的方法的复杂性。

1 本文算法设计

图1显示了提出的标签完备的结构，主要包含了标签的语义相关性、整体视觉多样性和优化计算。对于标签的语义相关性测量，引入NMF发现标签间的缺失关系。然后，利用图像之间的总平方差来衡量标签的整体视觉多样性。最后，引入两个正则项来降低计算复杂度。图1(a)部分为用户提供的图像矩阵，图1(b)为非负矩阵分解过程，图1(c)为计算整体视觉多样性，图1(d)为通过正则项优化并进行重构，生成了最后的标签图像矩阵。根据图1得出，经过一系列的运算，得到的标签图像能更细分图像内容，对相似内容具有更好的描述。

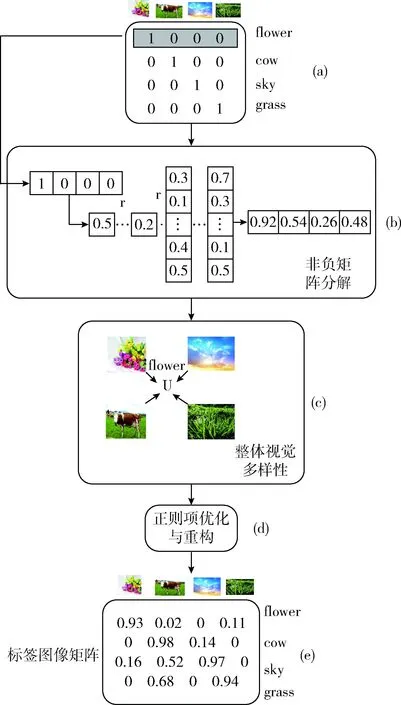
图1 图像标签完备结构

标签的目的是估计已完成的标签图像矩阵T,T(i,j)表示将标签t(i)分配给图像x(j)的概率。在本文中，将通过优化框架来估计完备的矩阵T。

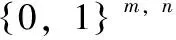
minTDs(T)+λcDc(T)+λrDr(T)

(1)

本文算法流程如图2所示。

图2 本文图像检索算法过程

1.1 非负矩阵分解

矩阵分解技术可以看作是将原始矩阵映射到子空间，并求出原始矩阵的低秩近似值[8]。因此，矩阵分解技术可以用来发现对象之间的关系，已有的方法是在矩阵分解中引入不同的约束条件，例如主成分分析(PCA)和部分潜在语义分析(LSA)。在矩阵分解技术中，NMF比其它技术有更优越的性能[9]。针对不同的应用，本文中提出了基于传统NMF的改进方法，在标签图像矩阵中，负数项不能很好理解，因此，其约束条件为矩阵中元素为非负项，也就是所有元素必须等于或大于零。因此，利用非负矩阵分解可以发现标签之间的相关性，并利用分解因子的乘积来完成缺失标签的重构。

正如我们已经讨论过的，重建矩阵T的成本最小化可以通过以下方法来解决

(2)

其中，T≈WH,i,j,a,b为矩阵中的指标。对于已知T，寻找非负矩阵W,H，使T≈WH。通过分析可理解为：T的列向量为多W中列向量的加权和；而权重系数为H相对的列向量。因此，W可称为基矩阵，H可称为系数阵。对此，通过利用系数矩阵代替原矩阵，可完成对原矩阵降维，获得数据特征的降维处理，从而减少运行空间，提高效率。

为简化书写，T(i,j)可表示为Tij。W,H为矩阵T的分解因子。此外，W,H可理解为系数矩阵W和基矩阵H的乘积。从这个角度看，基矩阵H描述了潜在的低秩子空间，通过H可以发现标记的相关性。因此，目标函数Ds(T)可定义如下

(3)

1.2 整体视觉多样性

通过NMF探索了标签的语义关系，同样，也考虑图像的视觉内容之间的关系[9]。具有相同标签的图像在内容上更相似，在视觉特征空间中彼此接近。因此，视觉特征空间中的图像差异可以称为视觉多样性。在本文中，利用图像之间的差异和标签特性方式来描绘视觉多样性，对于标签完备问题，具有相同标签的图像在标签完备后可能更接近，视觉多样性应该更低[10]。

为了减少所有图像的整体视觉多样性，需将图像的整体平方差与减少。对于Ti,j来说，其表示第i标签相对于第j个图像的概率，概率Ti,j可以作为计算图像的加权平均的权重，图像的均值越高，其概率越高。基于这一观察，可以对整体视觉多样性Dc(T)进行计算

(4)

其中，vjz为第j图像视觉特征向量vj的第z个成分。d为视觉特征vj的维度。ui为第i个标签视觉特征的第2个成分所对应的加权平均向量，表示如下

(5)

结合vj的行与列，构建视觉特征矩阵V，表示如下

(6)

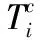
(7)

因此，整体视觉多样性Dc(T)通过矩阵形式表示为

(8)

其中，“·”为点积运算。

1.3 正则项优化

本文引入两个条件作为正则项来控制优化框架的复杂性。①已完备的标记图像矩阵不应与原始用户提供的标记图像T矩阵发生显著变化，因此，利用已完备的标签图像矩阵与原始标记图像矩阵T0的差异来惩罚它们的变化。②标签图像矩阵可能是稀疏的，因为每个图像通常标记的标签比整个标签集少，因此，通过标签图像矩阵的Frobenius范数来表示T的稀疏性[11]。

结合上述提到的两个条件，正则化项Dr(T)的函数表示为

(9)

通过对非负矩阵分解、整体视觉多样性、正则化项的描述，将这3个过程线性结合起来，形成了一种优化框架，定义如下

(10)

初始化：0<β<1,0<σ<1

执行：Xk+1=P[Xk-αk▽f(Xk)]；

iff(Xk+1)-f(Xk)≤σ▽f(Xk)(Xk+1-Xk)

doαk+1=αkβ；

elseαk+1=αk；

end

在将投影梯度法应用于最优化问题之前，先介绍下基本投影梯度法。在算法1中给出了边界约束优化的基本投影梯度法。投影梯度法是一种迭代方法，计算变量的梯度，并在每次迭代中沿着梯度的负方向更新变量[13]。参数α决定步长大小和变化，可变步长保证了每次迭代目标函数值逐渐减少。在算法1中的分段函数P[.]定义如下

(11)

其中，u,l分别为变量x的上下边界。

在本文中，通过交替迭代将基本投影梯度法推广到标记完备问题上。定义式(10)中的目标函数为f(T,W,H)，其在W,H,T处的梯度计算分别表示如下

▽Hf(T,W,H)=(WH-T)WT

(12)

▽wf(T,W,H)=(WH-T)HT

(13)

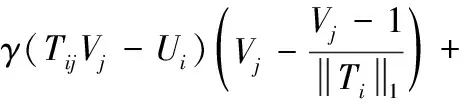
(14)

根据式(12)～式(14)的梯度函数，W,H,T的更新规则定义如下

Hk+1=P[H-αh▽Hkf(T,W,H)],lh=0

(15)

Wk+1=P[Wk-αw▽wkf(T,W,H)],lw=0

(16)

Tk+1=P[Tk-αt▽Tkf(T,W,H)],lw=0,ut=1

(17)

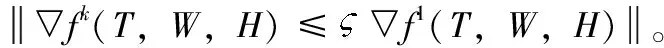
算法2: 标签完备问题的交替投影梯度法

执行：

a.确定T，计算W,H的最优解；

重复 根据式(15)～式(16)计算Hk+1,Wk+1，根据更新规则更新aw,ah；

k=k+1；

Until 收敛

b.确定W,H，计算T的最优解；

重复 根据式(17)计算Tk+1，根据更新规则更新at；

k=k+1；

Until 收敛；

END

1.4 相似度量

图像由多个标签语义构成，其视觉特征可以用标签语义集表示[14]。标签作为图像描述的元数据，可表征其语义内容。图像语义内容越相似，视觉特征也越接近；相反，图像语义内容相似度越低，视觉特征差异越大[14]。

在一组图像集中{d1,d2,…,dn}，设第i个图像di；t(di)为图像全部标签集；t(di)={t1di,t2di,…,tndi};m为di中标签数。对于图像di与dj的标签差异Score(di,dj)为

(18)

其中，dis(t(di),t(dj))为di与dj的标签语义距离，sim(t(di),t(dj))为di与dj的标签语义相似性。

2 实验与分析

为对提出的算法性能测试，在3个常用的数据集中测试：Flickr25K，VOC2012。测试条件为：Intel i5 4核CPU，3.50 GHz，8 GB RAM，64位WIN8系统。测试平台为Matlab2010。为突显本文算法的优异性，选取当前流行的检索算法：文献[5-7]对比，为便于记录，依次记为A算法、B算法、C算法。

2.1 数据集

Flickr25K是来自Flickr中的25 000图像构成[15]。该数据库含有38种语义标签，每幅图像拥有若干个标签，平均每幅图像的标签2.8个。随机选取其中的2000幅为测试集，剩下的图像作为训练集。

VOC2012数据库共有11 530个图像[16]，20 种标签，平均每个图像拥有的标签数为2.8个。随机选取其中的2000幅图像作为测试集，剩下的图像作为训练集。

2.2 评价指标

为衡量算法的性能，利用平均累计收益(ACG)与平均相似度(MAP)作为算法的评价指标，定义如下[17]：

平均累计收益(average cumulative gain，ACG)是返回的前m个图像的平均相似度，表示如下

(19)

其中，r(i)为第i个返回和查询图像相同的标签数。

MAP 是查询集中所有图像的平均检索准确度

(20)

其中，M为查询图像库的大小；APw为每幅图像的平均相似度，定义为

(21)

其中，δ为指数函数。当在相似度级别p所返回图像数量(rp)大于0时为1，反之为0。

2.3 实验结果

为了评价TBIR性能，通过精度对算法统计，给定指定的标签后，该算法根据标签的概率返回搜索的图像。图3为在Flickr25K数据集中进行两组实验，分别返回图像数N=10与N=20。对指定标签的图像都会返回，可以看出，对不同的标签得到的返回精度相差较大。对比返回图像数N=10与N=20，当对每个图像的更多标签进行评估时，标签完备的影响更为有效。

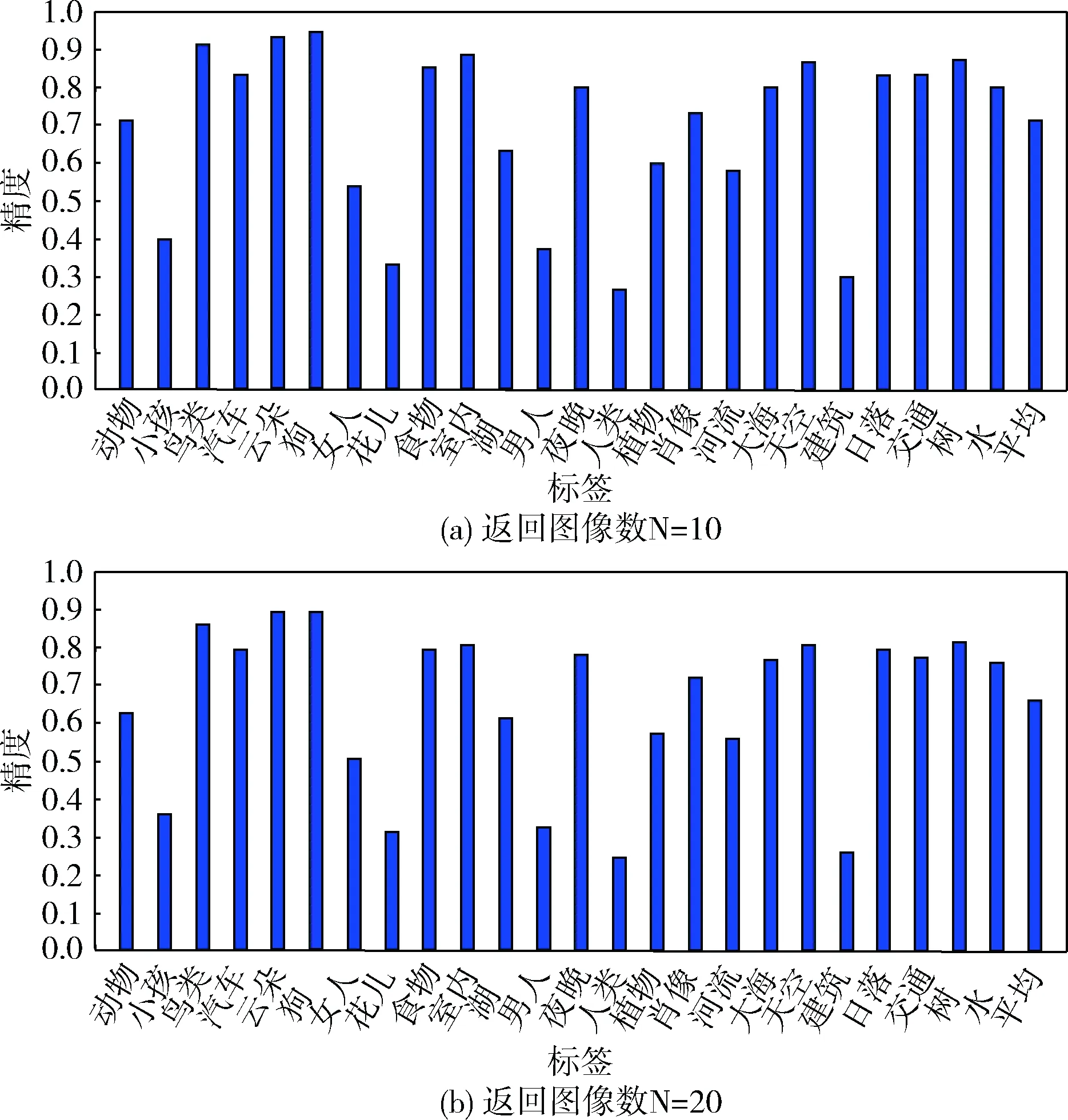
图3 Flickr25K图像集中不同返回图像统计

图4为查询图像，图5～图8为分别通过不同方法得到的最相似的9幅返回图像。从返回图像中看出，图5中本文算法得到的返回图像与查询图像相似度最高，基本上都包含了查询图像中的重要目标(苍鹭与树枝)。图6中返回的结果中误返回了一只白鹭图像。图7中误返回了2幅麻雀图像。图8中误返回了绿鹭、含有较多树林的建筑图像。实验结果表明：相对其它3种算法，本文算法具有较高检索精度，返回的图像与查询图像相似度高。主要是因为本文对图像进行NMF，利用NMF可以发现标签之间的相关性，得到了图像的基矩阵与系数矩阵。为了考虑图像的视觉内容，更好辨别内容相似的图像，在NMF过程中嵌入了整体视觉多样性，利用图像之间的差异和标签特性方式来描述绘视觉多样性。同时为保证标签图像矩阵的正确校正和稀疏性，引入两个正则化因子对其进一步优化，并根据分解因子的乘积来完成缺失标签的重构，得到标签图像矩阵。为了更好完成检索，提高精度，通过计算图像矩阵的标签语义距离进行相似性度量，完成图像检索。而A算法中不能同时有效含有多个目标的复杂图像，对含有多个目标的复杂图像时，其只用一个哈希码不能准确描述每个目标，检索性能不佳。B算法对于简单点的图像能够有效检索，但对于较复杂的图像时，其检索精度不高，易出现语义鸿沟，且对参数较敏感。C算法中在多标签数据集上能较好提高检索性能。但对于图像标签不完整、模糊、含噪声时，易导致图像检索精度不理想。

图4 查询图像

图5 Flickr25K数据集中本文算法检索

图6 Flickr25K数据集中A算法检索

图7 Flickr25K数据集中B算法检索

为了准确评估算法的性能，分别在Flickr25K，VOC2012中测试ACG与MAP，结果如图9、图10所示。根据图9中，在Flickr25K中，本文算法得到的ACG与MAP曲线均优于对照组算法，随着返回图像数量的增加，曲线逐渐降低，变化平稳，图10为在VOC2012数据库中得到的ACG与MAP曲线图。依据图10得知，随着返回图像数量的增加，曲线逐渐降低，变化平稳。图9与图10得到ACG与MAP曲线结果表明本文算法的检索性能最优。

图8 Flickr25K数据集中C算法检索

3 结束语

针对于图像标签不完整与模糊，标签丢失等易导致图像检索不准确等不足，提出了一种TBIR算法。通过联合标签的语义相关性和图像的视觉相似性来完成并优化标签图像矩阵。图像和标签之间的关系可以用标签图像矩阵表示，标签图像矩阵的元素反映了标签与图像间的相关性。因此，利用NMF对潜在的低秩空间中发现标签之间的相关性。为更好辨别内容相似的图像，在NMF过程中嵌入了整体视觉多样性，通过最小化图像之间的总平方差和标签特定的方法来减少标签的整体视觉多样性。引入两个正则化因子对其进一步优化，降低复杂性，并根据分解因子的乘积来完成缺失标签的重构，得到标签图像矩阵。为了完成图像检索，通过计算图像矩阵的标签语义距离进行相似性度量。实验验证了提出算法具有优异的检索性能，获得良好的ACG与MAP评价指标。

图9 Flickr25K 数据集测量结果

图10 VOC2012数据集测量结果