基于非线性尺度空间的增强现实场景识别算法

寇 兰，秦鸣谦，赵新雨，黄宏程

(重庆邮电大学 通信与信息工程学院，重庆 400065)

0 引 言

增强现实(augmented reality，AR)[1-3]是当前计算机视觉领域的研究热点，它是由虚拟现实技术发展而来，通过在真实场景中添加虚拟信息增强人们对于真实场景的认知。场景识别则是一套增强现实系统中非常关键的一个环节[4]，特征点匹配则是其中的关键技术。SIFT(scale invariant feature transform)算法的应用[5]是特征检测和图像匹配中的一个里程碑，信息量大，独特性好，它被广泛应用在很多不同的领域，如目标识别，但此算法的运算量过大、匹配速度慢；受到SIFT算法的启发，SURF(speeded up robust feature)算法[6]运算速度明显增快，并且同样具有缩放旋转不变性，对照度和视点变换也具有一定的鲁棒性；而BRIEF(binary robust independent elementary feature)算法[7]在图像匹配中，计算速度和识别率等方面都超过了SIFT和SURF。

SIFT、SURF的特征描述对视点变换、照度变换、模糊、旋转缩放变换等都有一定的鲁棒性，但由于其描述符维数比较大，分别为128维和64维，导致每个描述符所占的空间比较大，因此造成后续的搜索和匹配时间消耗增大，识别速度下降，这对于对实时性要求很高的增强现实应用而言是相当不利的。而BRIEF算法与SIFT、SURF相比，在生成描述符和描述符匹配的时间消耗上低于前两种算法，速度明显增快，但是由于在BRIEF算法中是用二进制串对特征点进行描述，所以它对噪声比较敏感，而且不具备旋转不变性和尺度不变性。ORB(oriented fast and rotated brief)算法[8-10]对特征点描述的细致程度要低于SIFT和SURF，但在计算速度上要明显快于SIFT和SURF。作为一种局部不变特征描述符，ORB具有旋转不变性，但不足的是该算法并不具备尺度不变性，对于图像的缩放变换鲁棒性较差。其根本原因在于ORB算法采用FAST(features from accelerated segment test)[11]算法进行特征点提取，但是FAST算法没有赋予特征点尺度不变信息，因此使得ORB描述符不具备尺度不变性。文献[12-14]分别利用SIFT和SURF算法的思想使描述符具备了尺度不变性。但这种基于高斯金字塔的改进方法造成边界模糊和细节丢失，使特征点检测错误率增高，而采用建立非线性尺度空间提取特征点的方法可有效弥补此方面的不足[15,16]。

1 基于非线性尺度空间的特征点提取

1.1 非线性尺度空间的建立

由于欧拉法在收敛时步长非常小，迭代次数多，计算成本高，所以在求解非线性扩散方程时若用传统的正向欧拉法效率会很低。由此，本文在进行非线性扩散滤波时使用加性算子分裂算法(additive operator splitting，AOS)[17]，这样对于任意步长都可以获得稳定的非线性尺度空间。

通常利用非线性偏微分方程对非线性扩散滤波方法进行描述，如式(1)

(1)

为了降低边缘位置的扩散，增加区域内部的平滑程度，函数c(x,y,t)可以根据梯度幅值的大小来进行设定。函数g的形式有如下几种

(2)

(3)

(4)

c函数选择g3够平滑区域内部并且避免边界信息的丢失[18]。参数k是控制扩散级别的对比度因子，k的值越大，边缘信息丢失得越多。在本文中，参数k的值设为图像平滑后的梯度直方图75%百分位上的值[18]。

因为非线性偏微分方程没有解析解，所以，本文先将方程式(1)离散化，转化为如式(5)的隐式差分格式

(5)

式中：Al是表示图像在各维度(l)上传导矩阵。该方程的解如下

(6)

式中：I表示单位矩阵；m表示显性扩散步数；τ表示时间步长。

为了能够针对不同图像的检测都能保持较高的正确率，本文采用一种自适应选取尺度空间组数的方法[18]：

构造尺度空间，尺度级别按对数递增，尺度参数σi为

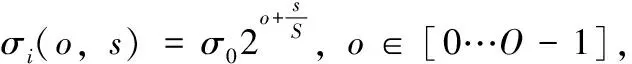
(7)

式中：o表示组；s表示层；σ0表示尺度参数的初始值；O为总组数；S为总层数；N=O×S为整个尺度空间包含的图像总数。O和S太大会花费过多时间构造尺度空间，而O和S太少会造成匹配率降低。在本文中，将S设为经验值4，再按照式(8)来获取O的值

(8)

式中：c为输入图像的行数，r为输入图像的列数；[]表示取整。

非线性滤波扩散模型是以时间为单位，因此需要将离散空间内以像素为单位的参数σi转换为时间单位，按照式(9)求出进化时间ti，最后将ti根据式(6)求得相应尺度图像

(9)

具体非线性尺度空间的建立流程可参见文献[17]，最终可求得到非线性尺度空间的所有图像，结果为式(10)

(10)

1.2 特征点提取

本文采用FAST算子来对特征点进行提取，FAST算法的原理是若在某个待测点周围有满足一定数量的像素点的特征与该点不同，则认为该点为角点。FAST算法具体定义请参见文献[11]。在非线性尺度空间每一层都采用FAST算法检测特征点，并将检测得到的特征点所在非线性尺度空间的组数o与层数s记录下来。求出候选点及其FAST分数V，V是候选点和以它为圆心的Bresenham圆上16个像素点绝对偏差的和。若候选点的分数V大于其同一尺度层中的8个相邻点以及与其相邻的上下尺度层中的9×2个点，则保留此候选点。

FAST算法检测出的特征点不具有旋转不变性。所以使用强度中心[11]的方法让特征点具备方向信息：将特征点作为原点在取点区域U内创建坐标系，计算出特征点在U内的质心位置，以原点到质心坐标的向量方向作为特征点的方向，计算步骤如下所示：

区域U的矩定义为式(11)

(11)

式中：I(x,y)是图像的灰度表达式，该矩的质心为C=(Cx,Cy)。其中Cx=M1,0/M0,0，Cy=M0,1/M0,0，那么FAST特征点的方向为

θ=arctan(M0,1/M1,0)

(12)

2 特征点描述

在特征点描述上本文采用BRIEF算法[19]，BRIEF算法利用二进制串对图像区域进行描述，不仅节约了存储空间，而且大大减少了匹配时间。

以特征点为中心定义S×S大小的邻域窗口P，在窗口内随机取一个点对(x,y)，以式(13)为准则进行二进制赋值

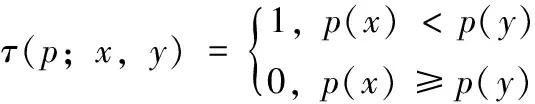
(13)

式中：p(x)、p(y)分别是像素点x、y处的灰度值。选择n个点对时，根据式(13)得到n维二进制码串的描述符，如式(14)所示

(14)

在本文中将n的值设置为256。由于采用二进制码串对图像区域进行描述，会产生噪声敏感的问题。为此，采用积分图像来解决此问题：在31×31的窗口中，随机产生一对点对后，分别以随机点为中心，两个5×5的子窗口，然后比较两个子窗口内的灰度值之和的大小进行二进制赋值[8]。

根据以上方法的特征描述符并没有包含方向信息，因此需要把1.2节中获得的特征点方向θ作为描述符的主方向，使其具有旋转不变性。对于(xi,yi)处的领域内选取任意n个点对集

(15)

通过旋转角度θ形成相应的旋转矩阵Rθ，构建Sθ=RθS，这样的BRIEF描述符便具有旋转不变性。如式(16)所示

gn(p,θ)=fn(p)|(xi,yi)∈Sθ

(16)

通过贪婪搜索，将计算得到的所有像素点对中关联性最低的n个作为具有旋转不变性的BRIEF特征。

3 目标匹配

本文中的目标匹配分两步进行，分别为特征点匹配和目标查找。

(1)特征点匹配。因为采用二进制码串对特征点进行描述，所以采用计算汉明距离来判断特征点是否匹配。采用层次聚类算法检索匹配的特征点，寻找与查询图像特征描述符距离最近的样本特征描述符，设定一个阈值Rth，当两者之间的距离低于Rth的时候，则认为这两点为一对匹配点，特征匹配。

(2)目标查找。将查询图像的全部特征描述符都在训练样本中进行最近邻查找，本文通过设定特征点的正确匹配率来对查询图像是否和样本图像属于同一场景进行判断。设e为当前查询图像特征点的总个数，nmax为样本图像最大匹配点数,r为样本图像的匹配率，如式(17)，thd为特征点匹配率阈值

(17)

当r>thd成立时，说明查询图像与样本图像的匹配程度比较高，便可认为查询图像与此样本图像为同一场景。

4 实验结果与分析

4.1 实验条件

计算机配置：处理器为Intel Xeon E3-1231 V3，主频为3.4 GHz。操作系统为Windows 10 64位系统，编程环境为Visual Studio 2010与opencv 2.4.10。

实验数据分为两组：一组为Mikolajczyk 05标准测试图集，如图1所示，该数据集分为8个子集，共有5种变换：视点、模糊、照度、JPEG压缩，以及尺度和旋转。另一组为国际图像标准库UKBench，如图2所示，一共有2550个不同物体，每个物体包含了从4个不同视角拍摄的图像，共10 200幅。

图1 Mikolajczyk 05标准测试图集

图2 UKBench数据集

4.2 实验过程

算法流程如图3所示，分为训练阶段和识别阶段。训练阶段计算数据集中的图像的特征点描述符存入容器中，识别阶段计算查询图像的特征点描述符，然后进行图像匹配。

图3 本文算法流程

4.3 算法评估

4.3.1 性能对比

将本文算法和SIFT、SURF算法进行对比实验，利用图1中的5组测试图像，对识别算法的正确匹配率(样本图像最大匹配点数与查询图像特征点的总个数的比值)进行对比分析。算法正确匹配率如图4所示。对于这5种变换条件下的图像识别结果，从匹配率看，由于本文算法的非线性尺度构建以及自适应选取尺度空间组数，在视点变换、缩放旋转变换和JPEG压缩下，正确匹配率均高于SIFT、SURF算法，而在模糊和照度变换下，本文算法略低于SIFT、SURF。本文算法相对于SIFT、SURF能得到较高的匹配率，并且在视点、缩放旋转和JPEG压缩变换下具有较高的鲁棒性。

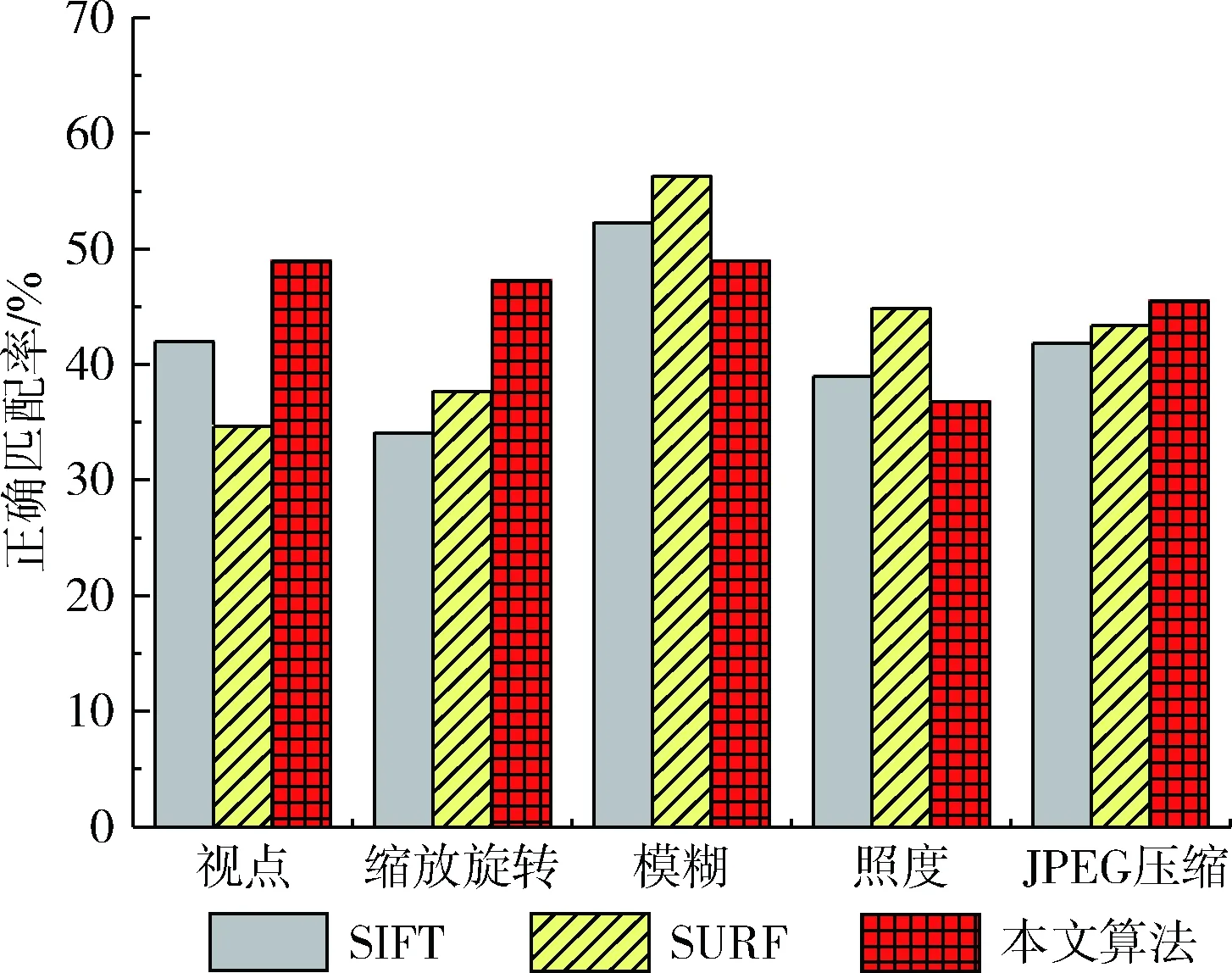
图4 算法正确匹配率对比

4.3.2 算法训练时间、识别时间和识别精度对比

本文从训练时间、识别时间和识别精度3个方面与SIFT算法和SURF算法进行对比。训练时间：训练开始到训练结束所花费时间；识别时间：从获取图片到识别结果出现所花费的时间；识别精度：识别成功的次数与识别总次数的比值。

每次实验随机选取不同的场景，每个场景里任意选取3个不同视角的图片作为训练样本，将剩下一张作为测试样本。实验结果取100次测试的平均值。

图5是算法训练时间对比。从图5中可以看出，本文算法在训练中用时最少，相较于SIFT和SURF算法具有显著优势，SIFT算法用时约为本文算法的15倍，SURF算法用时约为本文算法的3倍多。

图5 算法训练时间对比

图6是算法识别时间对比。从图6中可以看出，本文算法和SURF算法的完成识别所花费的时间都明显少于SIFT算法，而SURF算法平均识别时间在样本数少时与本文算法相差不多，但是当样本数量增多时便高于本文算法，约为本文算法的1.25倍。实验结果表明，本文算法在识别时间优于另外两种算法，且平均识别时间在0.5 s以内，具有良好的实时性。

图6 算法识别时间对比

图7是算法识别精度对比。由图7可以看出，在样本库的数量比较小的时候，本文算法和另外两种算法的识别精度都比较高，识别率都保持在90%以上；但随着样本库的不断增多，3种算法的识别精度都在不断降低，其中SURF算法下降的趋势较其它两种算法最为明显，本文算法识别精度稍微低于SIFT算法。实验结果表明，本文算法在不同大小的图像样本库中都达到了较高的识别精度。

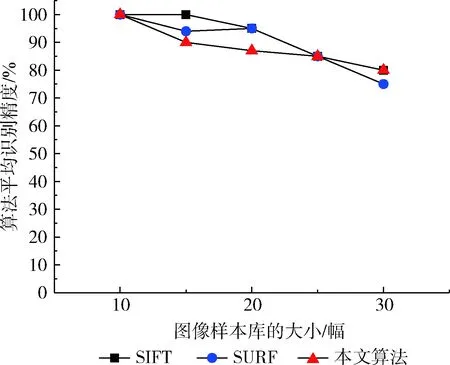
图7 算法识别精度对比

5 结束语

本文提出的场景识别算法在特征提取方面通过构建非线性尺度空间，用FAST算法对非线性空间每一层进行特征点检测；然后采用具有旋转不变性的BRIEF特征描述算法进行特征描述；在进行目标匹配时首先采用层次聚类算法进行特征点匹配，然后通过最近邻算法进行目标查找。实验结果表明，本文算法在场景识别上展现了良好的效果，在视点变换、尺度旋转变换和JPEG压缩的变换下具有较强的鲁棒性，而且在可以实现快速场景识别的同时，还能够达到较高的识别精度。本算法也有不足之处，当训练样本数量太多时，识别时精度会下降，所以无法支持大规模场景识别，下一步的计划是研究如何改善这一问题。