基于格的属性签密方案

汤海婷，汪学明

(贵州大学 计算机科学与技术学院， 贵州 贵阳 550025)

0 引 言

属性密码[1-3]是对身份密码体制[4,5]的延伸和扩展。S和W两人提出属性密码[6]的原型。之后，随着访问控制结构的加入，使得属性密码体制更为灵活性。Zheng提出了签密这种密码学原语[7]，它改变了以往先签名后加密的模式，使得签名和加密能同时完成，极大提高了计算效率。在身份签密这一领域，有不少国内外学者已经陆续做出研究。随着量子时代的到来，越来越多的学者利用格理论来提高身份签密的安全性。Lu等提出了格上模糊的身份签密方案[8]；项等提出具有前向安全的格上的身份签密方案[9]；Lu等又提出了无陷门的格基签密方案[10]。格上的属性加密和签名方案[11-16]陆陆续续得到关注，史妍等很早就设计了基于双线性对的属性签密方案[17]。然而，格上的属性签密方案一直以来都鲜有问津。Xiang等研究了隐藏访问控制结构的格属性签密方案[18]。闫建华利用变色龙hash函数，变种算法等在标准模型下，设计了格上的属性签密方案[19]。本文以Lu等设计的模糊的身份签密方案[8]和文献[16]格上的属性签名方案为基础，构建了基于格的属性签密方案。格密码被认为是可以抵抗量子攻击的密码体制，同时，格上的加解密等运算量相比双线对运算量是大大减少的。因此，利用格来构造的属性签密方案其安全性和效率都会相对得到提高。本文最后利用随机预言模型，对方案的安全性进行了简单的分析，验证了方案在格的两个平均困难问题下能够达到选择明文攻击的不可区分性和选择访问结构选择消息攻击下的存在性不可伪造性。

1 格理论和属性签密

1.1 格理论相关定义

定义1 格的定义:格的定义是基于向量空间。假设有线性无关的向量v1,v2…,vn∈Rm。由向量v1,…,vn的线性组合生成格L，即L={a1v1+a2v2+…anvn:a1,a2,…,an∈Z}。

定义2 如果向量的坐标均为整数，比如：Zm={(x1,x2,…,xm):x1,x2,…,xm∈Z}，那么它就是整数格。如果m大于等于1时，那么整数格是Zm的加法子群。

定义3 如果H是一个概率多项式级算法。算法会输入安全参数k，得到{0,1}*→{0,1}k。如果算法满足高效性和抗碰撞性，那么H称为抗碰撞HASH函数。

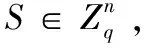
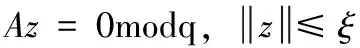
其它的相关原像抽样算法和格理论知识见文献[8,12-16,18]。

1.2 安全性攻击模型

定义6 IND-sCPA：选择明文攻击的不可区分性。EUF-SCMA：选择消息攻击下的存在性不可伪造性。具体定义见文献[20]。

1.3 格上的属性签密

本文的方案结合文献[8]的思路，具体形式化描述如下：

(1)初始化：输入安全参数，得到系统公共参数和主密钥。

(2)解签密密钥生成：输入主私钥，用户属性集θ，输出解签密密钥。

(3)签名密钥：签名密钥和本文用到的签名算法有关。

(4)签密过程：输入消息MSG，用户的属性集W。访问控制策略为Lpolicy，如果W|=Lpolicy，输出相对应的密文。

(5)解签密过程：输入签密的密文，如果接收者的属性集和发送方的属性集的交集满足门限值，且W|=Lpolicy。得到明文MSG，并验证明文和签名的有效性。如果验证成功，返回明文MSG。

2 格上属性签密方案的具体构造

文献[8]构造了第一个格上的模糊的身份签密方案，本文的方案构造结合文献[8]的构造方法，签名部分则利用文献[16]提出的签名方法。

2.1 方案描述

假设属性全集记为K，本文的加密部分采用shamir的门限访问控制结构，本文的门限值设置为d。设签名过程要满足的访问控制策略记为Lpolicy。同时，假设发送方的属性集为W，接受方的属性集为θ，要签密消息的消息空间记为t。初始化阶段：

(1)输入安全参数n，q，m，其中m>5nlogq，q=poly(n)，q的值是素数，且非常大。

(3)设有下列hash函数

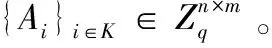
(5)系统参数PK={{Ai}i∈K,{Bi}i∈[t],A0,H1,H2,H3,H4,μ}，主私钥MSK={TA0，{TAi}i∈K}。

密钥生成：本阶段包括2.2节和2.3节两个部分。

2.2 解签密密钥生成

(2)假设用户的属性集为θ，对于i∈θ，Ri=H1(i)。

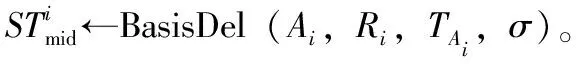
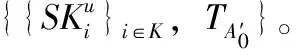
2.3 签名密钥生成

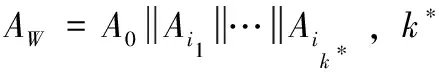
2.4 签密过程

(1)要签密的消息为MSG，输入W和Lpolicy。

(4)最终的签密密文为C={W,y1,y2,S3,Z,Cf,{Ci}i∈W}。

2.5 解签密过程

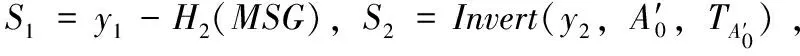
3 正确性证明

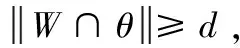
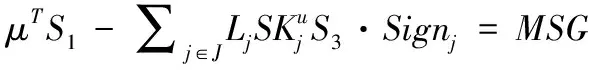
4 安全性分析

为了验证签密方案的可行性，不仅要在LWE问题下证明方案的IND-sCPA，还要证明方案在SIS问题下，满足EUF-SACMA。本文方案中涉及的签名方案是按照文献[16]来构建。因此这部分的安全性也是基于文献[16]。

4.1 IND-sCPA安全性分析

第一阶段：

(1)假设hash询问包含4个表L1，L2，L3，L4。

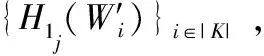
H2询问：发送方发送消息MSG*，挑战者收到消息后，如果表L2中存在，则返回。如果不存在，挑战者C产生消息MSG*对应的hash值，并存储在L2中。

H3询问：对于H3j(MSG,Lpolicy)，如果L3中没有找到对应的值。挑战者C随机选择一个H3j∈{0,1}t存于L3中，并做出应答。

H4询问：挑战者C先检查H4j是否在表L4中，若不在，则随机选择一个新的H4j∈{0,1}*，并且存在L4中，并将H4j发送给敌手。

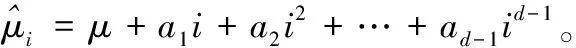
第二阶段：重复第一阶段。

猜想阶段：敌手A给出猜想b′，如果b′=b，预言机输出1。否则，挑战者C认为本实例来源于完全随机的取样器。

4.2 EUF-SACMA安全性分析

本阶段的Hash询问和上一阶段的游戏类似。选择要挑战的访问控制策略Lpolicy。

假如敌手A伪造了一个密文，如果密文有效。那么就能找到SIS困难问题的解。最后，给出本文方案和相关其它方案的安全方面对比，见表1。

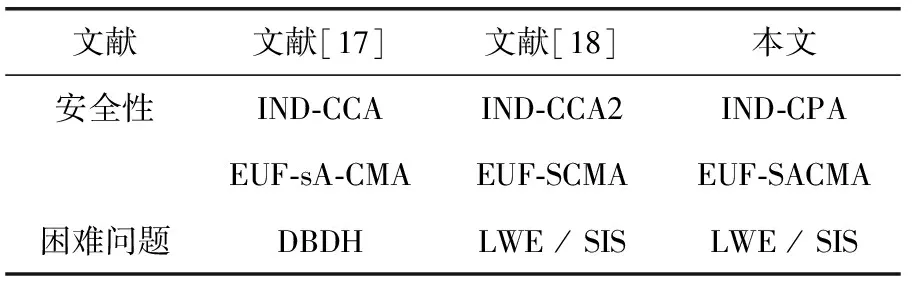
表1 ABSC方案比较

本文方案和文献[17]相比，本文的方案是利用格理论设计，因此安全性远高于基于双线性对的属性签密。和文献[18]相比，本文方案可以实现选择访问结构和选择消息攻击的存在性不可伪造性，但是不能满足文献[18]的选择密文攻击下的不可区分性。这也是下一步要解决的问题。

5 结束语

本文以文献[8]的思想为基础，提出一种基于格的属性签密方案，实现了选择访问结构和选择消息攻击的存在性不可伪造性。与传统的双线性对构建的属性签密方案相比，本文的方案更加安全，且减少了构建过程的运算量，具有更高的效率。下一步，将尝试构建格上安全性更高支持细粒度访问控制的属性签密方案，同时解决签密方案在选择密文攻击下的不可区分性。