基于CEEMDAN能量相对熵的小电流接地系统故障区段定位方法
2018-10-22张怡真
张怡真 金 涛
(福州大学电气工程与自动化学院,福州 350108)
随着我国配电网供电容量的不断增加,为限制短路点电流的大小,中性点经消弧线圈接地的运行方式被广泛采用[1]。在谐振接地系统中,单相接地故障的发生几率占总故障的 80%左右[2],对故障区段及时定位,影响着电力系统运行的安全性以及稳定性。
在故障区段定位问题中,被动式方法应用最为广泛,其又可分为基于稳态量[3]与基于暂态量[4-6]两大类。基于稳态量的定位方法在谐振接地系统中存在故障特征微弱、易受干扰等缺点,定位效果差,因此基于暂态量的区段定位方法是目前的研究热点。文献[4-5]利用小波及小波包变换来提取故障信号,但是其需要对母小波进行选取,不具有自适应性。文献[6]利用S变换来提取故障信息,根据上、下游的能量差异来识别故障区段,但是S变换在较高频带范围内对频域分辨的精确度不高,且很难对故障区段边界的时域特征进行确定。
CEEMDAN是一种新的自适应信号时频处理方法,能够解决传统EMD中存在的模态混叠等问题,本文将其应用于对故障信号的分析之中。本文首先对各区段装置上传的暂态零序电流信号进行CEEMDAN分解;再通过计算各区段能量相对熵来判断故障区段;最后在搭建的小电流接地系统模型中进行仿真测试。结果证明了所提算法的有效性。
1 暂态零序电流区段特征
建立如图1所示的小电流接地系统零序等效网络模型,以对单相接地故障发生过程中暂态零序电流区段特征进行分析。图中,M、N、P、Q分别为线路上的4个检测点;C01和C0n分别代表第1条和第n条健全线路上的等效零序电容;L0为消弧线圈的等效零序电感;假设第k条线路的NP区段上发生故障,在接地点加入一个虚拟电源来模拟故障,u0f和i0f分别为故障点等效零序电压和电流,如若将整个网络以故障处为分界,分为上、下游线路,那么该网络则可等效成两个彼此相独立的谐振系统。

图1 小电流接地系统零序等效网络模型
流经区段MN和区段PQ的电流分别为两个检测点的电流差,即

式中,iCmn和 iCpq分别为MN区段和PQ区段的对地电容电流。由于配电网中单个区段的长度通常不长,该对地电容电流相较于其他电流分量要小得多,可忽略不计,即 iM≈ iN(iP≈iQ),即故障点同侧的两处相邻检测点的暂态零序电流波形没有明显差异,且频谱分布相似。
但对于故障点两侧的两相邻检测点所检测到的暂态零序电流来说,两个等效的谐振系统之间相差很大,上游线路的对地电容远大于下游的值,使得故障点两边的零序暂态电流在谐振频率、幅值、衰减特性等方面存在巨大差异,在不同频率下的能量分布不同。图2展示了M、N、P、Q 4个检测点的暂态零序电流波形图,可以看到仿真结果与前文理论分析一致。

图2 各检测点暂态零序电流波形图
2 基于CEEMDAN能量相对熵的故障区段定位方法
2.1 CEEMDAN原理
CEEMDAN[7]是一种对 EMD[8]的改进算法,解决了传统 EMD中存在的模态混叠等问题,能够将复杂信号分解成有限个固有模态函数(IMF),分解得到的IMF能够突显原信号的局部特征信息。本文提出采用CEEMDAN方法来对各区段上传的暂态零序电流信号进行分解,可以完整清晰地将电流分解到各个尺度的频带内,其分解结果如图3所示。从图3中可以看到,分解结果中几乎没有残留的白噪声,能够有效地分解出故障电流信号中的各个分量,非常适用于对故障特征的提取。

图3 CEEMDAN分解结果
2.2 CEEMDAN能量相对熵
1)相对熵
相对熵(KLD)是统计学中的一个分析指标,假设有两个概率分布量 P = { p1, p2,… ,pn}和 Q ={q1, q2,… ,qn},利用相对熵就可以考量P和Q的分布相似度,其表达公式如下[10]:
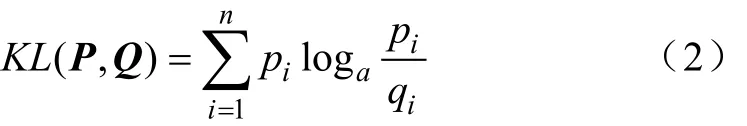
式中,n为频段个数;对数底数a通常取e为底数。相对熵是非负的,熵值越小,则代表P和Q两个分布越类似,反之差异越大;当且仅当P和Q两个分布完全相同,即 pi= qi时,熵值为0。
2)CEEMDAN能量相对熵
利用CEEMDAN方法对信息序列x(t)进行分解得到一系列IMF分量后,通过HHT带通滤波[11],将其分解至m个频带内,可以得到第 i(i = 1 ,2,… ,m )个频段的能量,即

式中, ai(n)为第i个频段内的第n个数据点。计算得到频段 i的能量之后,就可以得到其在所有能量中占有的比例:

根 据 相 对 熵理 论 , 定 义 信 号x(t)和x′(t)的CEEMDAN能量相对熵为

2.3 算法流程
在配电线路中通常存在多级分支,对于分支的处理,本文采用文献[4]中所提方法处理分支,即在区段定位之前,先算出分支节点前后区段检测点的能量相对熵值,将值小的区段所在支路选出用于后续的计算对比。
图4展示的是基于CEEMDAN能量相对熵区段定位方法的具体流程图。

图4 基于CEEMDAN能量相对熵区段定位算法流程图
3 仿真分析
为验证本文所提方法的有效性,利用Matlab建立含分支的小电流接地系统仿真模型,以出线5为例进行仿真分析,各区段线路类型及长度如图5所示,线路参数见表1。

图5 区段定位仿真模型

表1 线路参数
在仿真过程中,消弧线圈补偿度 p =8%,通过下式计算消弧线圈等效电感L和等效电阻RL,即
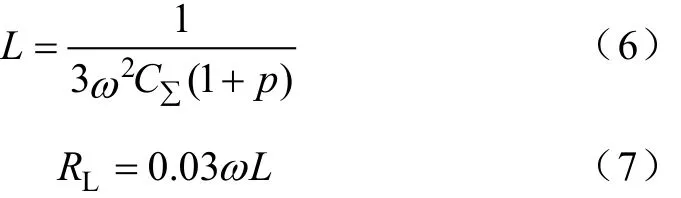
式中,C∑为系统对地电容之和。经计算得到 R=4.3034Ω,L=0.4566H。
在线路 5的不同区段设置在不同故障合闸角ϕ、经不同接地电阻Rf的情况下发生单相接地故障,采样频率为10kHz,利用CEEMDAN对故障后1个周期内的零序电流进行分解,CEEMDAN算法所加白噪声的幅值比值系数为0.2,循环次数N=25,分解后经带通滤波,将信号分为 20个频带(0~5000Hz),频带宽度为250Hz。先对分支处的测量点进行能量相对熵的计算,选择熵值较小的区段所在的支路用于计算比较(L51或L52),再对该支路其余区段的熵值进行计算,最后找到故障区段。在下表结果中,以D表示能量相对熵值,加粗值代表选中值。
1)在电缆区段(2-3/6区段)设置故障
缆-线混合线路的故障特征相比于单一类型线路复杂得多,因此本文对与架空区段相连的电缆区段(2-3/6区段)设置故障进行仿真,结果见表2至表5。

表2 ϕ =0°时支路选择结果
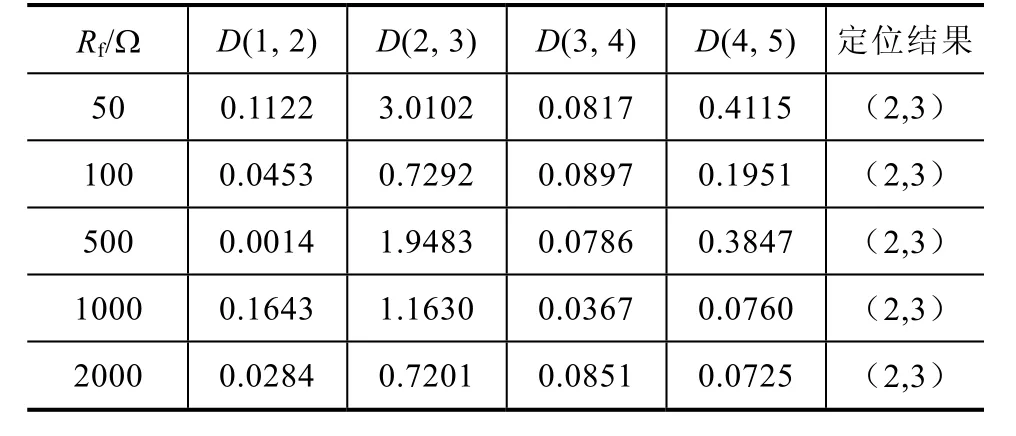
表3 ϕ =0°时区段定位结果

表4 ϕ =60°时支路选择结果

表5 ϕ =60°时区段定位结果
2)抗噪性检验
对方法的抗噪性能进行检验,在所提取的零序电流信号中加入 10dB的白噪声进行仿真,在区段(7-8)设置单相接地故障,不同故障情况下的仿真结果见表 6至表 7。从表中可以看到,故障区段的熵值明显高于非故障区段,可知本文所提方法在存在噪声的情况下仍有很高的定位准确率。

表6 含10dB噪声时支路选择结果
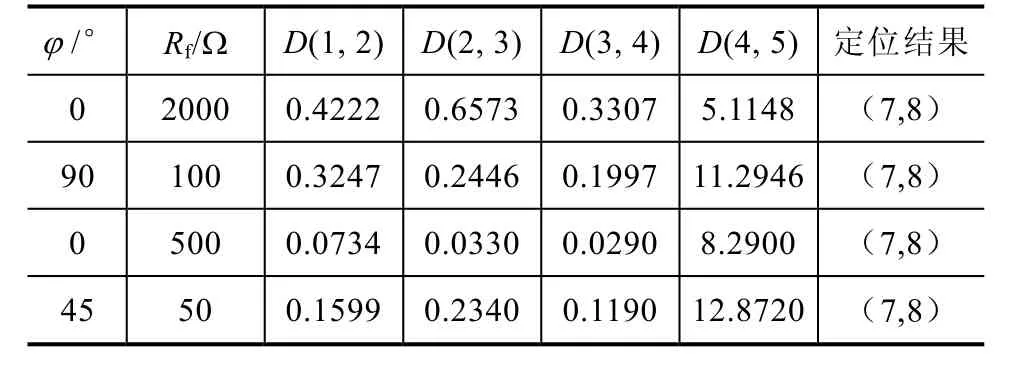
表7 含10dB噪声时区段定位结果
4 结论
针对配电线路区段的暂态零序电流特征,本文提出了基于 CEEMDAN能量相对熵的区段定位方法。经仿真验证,所提方法能够精确地定位出故障所在区段,不受故障合闸角、过渡电阻以及噪声的影响,具有可靠性强、实现简单、传输数据量小、允许对时误差、自适应性强以及抗噪性强的优点。
