动力定位船舶推力优化分配研究

刘 凯，文 武，夏 义



动力定位船舶推力优化分配研究

刘 凯，文 武，夏 义

（武汉船用电力推进装置研究所，武汉 430064）

针对动力定位船舶处于环境力较小而方向频繁变化的特殊海洋环境中定位作业的推力分配问题，采用组合偏置策略进行推力优化分配，研究了偏置量大小对组合偏置效果的影响规律，并针对组合偏置后存在能量消耗过大的问题，提出了基于能耗最优的二次推力分配方法。仿真结果揭示了偏置量不同对组合偏置效果的影响规律，验证了二次推力分配方法对降低推进系统组合偏置后能量消耗的有效性。

动力定位 组合偏置 能耗最优 二次推力分配

0 引言

在复杂多变的海洋环境中定位作业的船舶可能会由于单个或多个推进器的故障而失去预定位置，这种位置的丧失将导致严重的后果。因此，DP船舶的推进系统通常设计为过驱动系统，以满足DP船舶在任何情况下水平面上不同方向推力和力矩的需求[1]。关于推力分配优化问 题的建模与求解，有关学者已经做了大量的研究工作，取得了丰硕的研究成果[2,3]。

当船舶处于环境力较小而方向频繁变化的特殊海洋环境中定位作业时，采用常规的推力分配方法将会导致推进器的方位角也频繁地变化，但由于推进器本身的物理特性，方位角转动速度有限，很可能出现方位角的滞后现象而影响船舶的定位精度，同时也会加速推进器的磨损。针对这类问题，Kongsberg[4]提出了偏置的思想，即对DP船舶的推进器进行分组，允许推进器之间推力相互抵消。这种方法虽然额外消耗了部分功率，但避免了因推进器频繁转向而降低定位精度及加速推进器磨损等问题，在实际工程中有重要应用价值。Veksler[5]采用组合偏置算法以减少DP船舶在复杂工况下船舶电站的功率大幅度波动。国内学者施小成、魏玉石等人针对组合偏置算法提出了自适应组合偏置策略[6]，仿真结果表明自适应组合偏置策略能有效地提高船舶的动态性能，但是没有系统研究偏置量的大小对偏置效果的影响，而且在组合偏置后存在推进系统能量消耗过大的问题。

为揭示偏置量的大小对偏置效果的影响规律，解决组合偏置后存在推进系统能量消耗过大的问题，本文以一艘DP船舶为研究对象，将系统研究偏置量对偏置效果的影响，并提出二次推力分配算法以降低组合偏置后推进系统的能量消耗。

1 推力分配数学模型

1.1 目标函数

为了满足DP船舶的作业精度和燃油消耗率最小的要求，本文以船舶电站的能耗最小和推力偏差最小为目标函数：

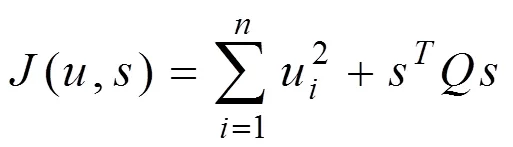
1.2 约束条件

1.2.1等式约束

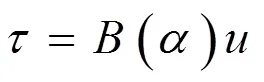
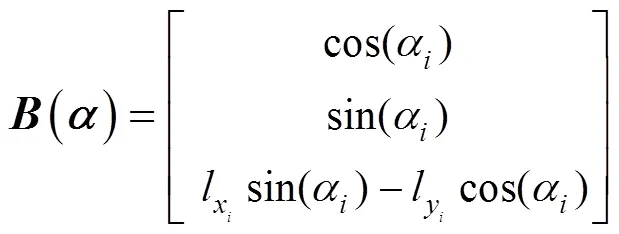
1.2.2不等式约束

在推力分配过程中，需要考虑各推进器的最大推力限制、推力变化率限制、全回转推进器最大角度限制及其转动变化率限制，则不等式约束可表示为：

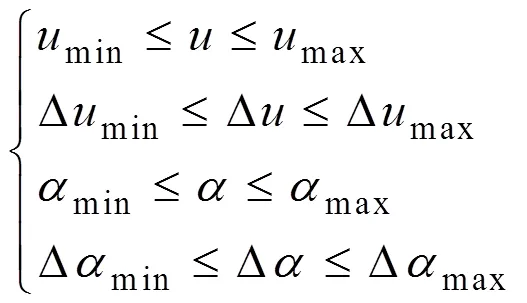
2 推进系统组合偏置算法

在船舶定位过程中，当外界环境力较小而方向频繁大角度变化时，采用推进器组合偏置的策略可以有效地解决全回转推进器方位角频繁大角度变化而导致方位角滞后的问题，从而提高船舶的定位精度，降低推进器的磨损。

2.1 组合偏置原理

组合偏置是指对DP船舶上的推进器进行分组，允许推进器之间的推力相互抵消，其中推力相互抵消量称为偏置量[8]。可以将偏置分为组内偏置和组间偏置，组内偏置是指允许组内全回转推进器之间的推力相互抵消；组间偏置是指将各个组内的全回转推进器等效成一个推进器，允许等效后推进器组之间的推力相互抵消。向外偏置是指两全回转推进器抵消力的方向背离两推进器连线的中点；向内偏置是指两全回转推进器抵消力的方向指向两推进器连线的中点。

2.2 组合偏置推力分配算法

图1 推进器布置示意图

将推进器1和2等效为一个推进器，则它们在X轴和Y轴方向的分力以及其产生的力矩可以表示为公式（5）。

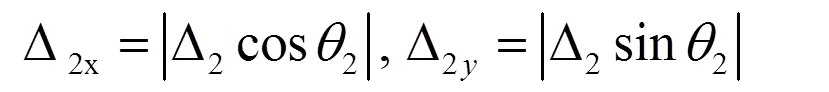
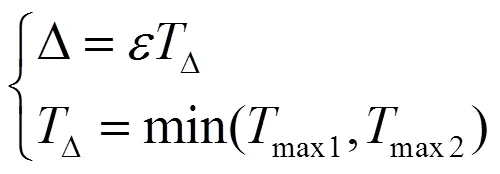
式中，为偏置量系数。

则自适应偏置量可以表示为：

2.3 二次推力分配方法

应用组合偏置推力分配算法得到的推进器角度变化是比较平稳的，但推进器推力大小相对于偏置前会大幅度增加，从而导致动力系统燃油消耗增加。针对推进系统能量消耗过大问题，本文提出二次推力分配方法，它的主要思路是在应用组合偏置法得到各推进器角度的基础上，以能量最优为目标，重新计算当前角度下的最优推力，避免推进器的方位角的突变，减小推进器的磨损，及燃油消耗。

二次推力分配方法的计算流程为：

1）通过优化算法求解推力分配问题，得到各推进器的最优推力和角度；

2）应用组合偏置将推进器分成不同等级的组，计算偏置量，得到偏置后的推力和角度；

3）通过二次推力分配方法计算当前角度的最优推力，得到推进器所需发出的推力以及偏转的角度。

3 仿真结果与分析

为了验证上述方法的有效性，本文以一艘DP船舶为对象进行计算机仿真研究。仿真中模仿DP船舶的定位过程，待分配力和力矩如图2所示。推进器的布置如图3所示，技术参数如表1所示，其中1号、2号、3号、4号全回转推进器的推力最大变化率为10 N ∙s-1，最大角度变化率为10 deg ∙s-1；5号和6号推进器的推力最大变化率为5 N ∙s-1。

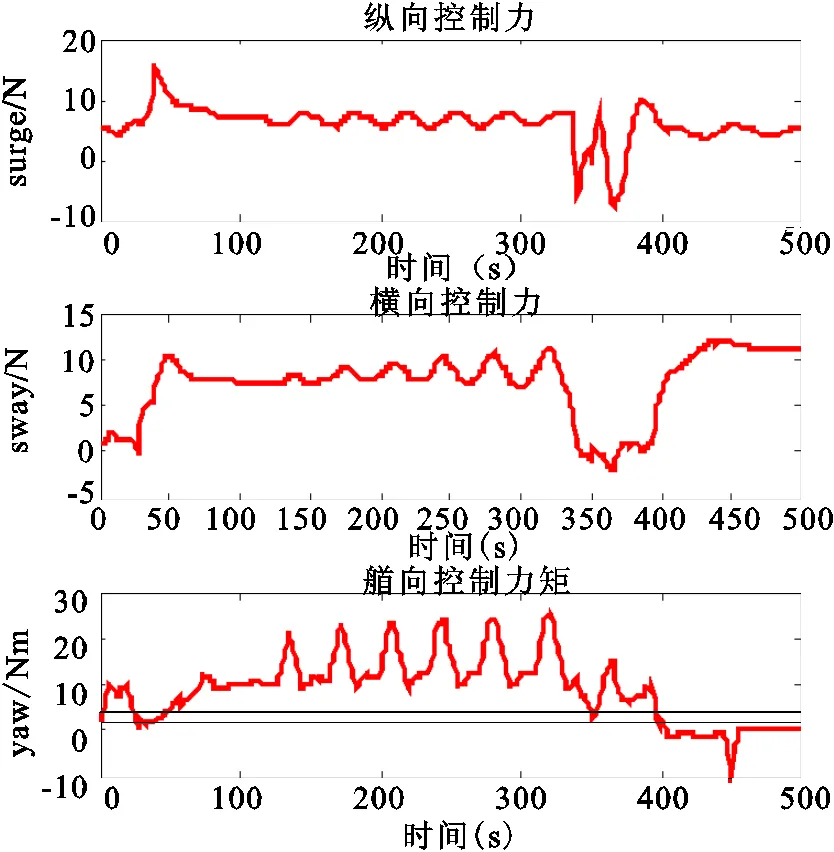
图2 待分配的控制力和力矩

图3 推进器布置图

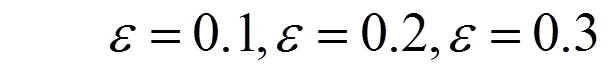
表1 推进器有关参数

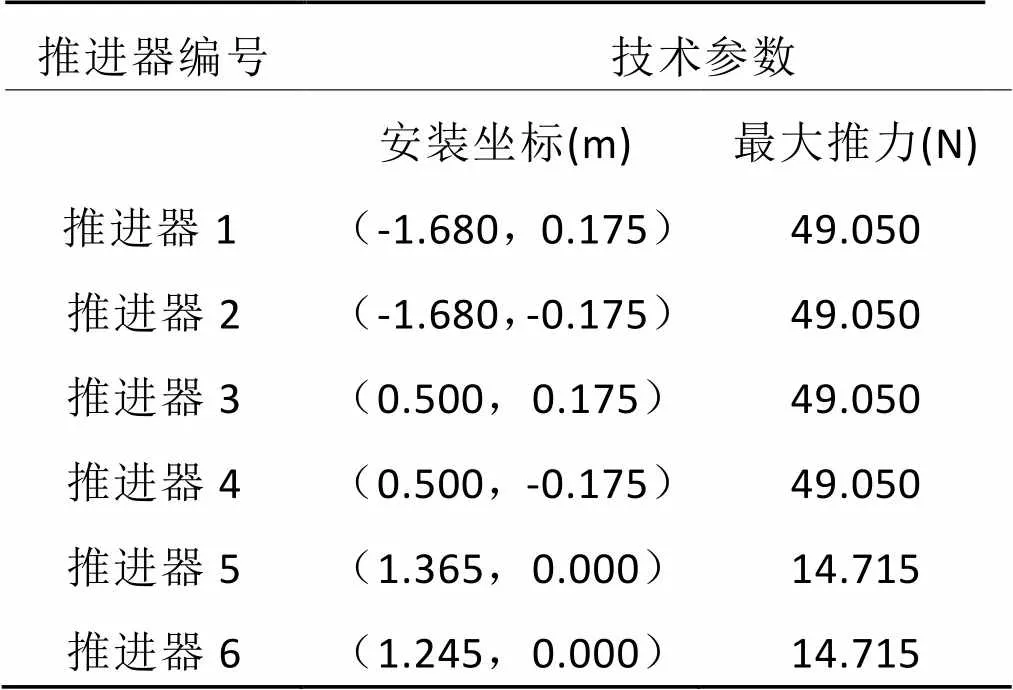
推进器编号技术参数 安装坐标(m)最大推力(N) 推进器1（-1.680，0.175）49.050 推进器2（-1.680，-0.175）49.050 推进器3（0.500，0.175）49.050 推进器4（0.500，-0.175）49.050 推进器5（1.365，0.000）14.715 推进器6（1.245，0.000）14.715

图4 推进器1推力变化

图5 推进器1方位角变化

图4和图5分别表示推进器1进行组合偏置后取不同偏置量时推力和方位角的变化曲线，图9表示推进系统进行组合偏置后取不同偏置量时能量消耗的变化曲线。从图5和图6表明随着偏置量的增大，推进器发出的推力也增大，而推进器方位角的变化越平稳，推进器的磨损也越小；比较当ε=0.2和ε=0.3时，推进器的角度变化相近，其中推进器1和推进器2的角度分别保持在40°和-40°附近，这样可以有效地减小两个推进器之间的水动力干扰，降低推进器的推力损失，但ε=0.3时推进器发出的推力比ε=0.2时发出的推力有较大幅度的增加，表明当偏值量处于某一临界值时继续增加偏值量对推力分配效果的改善很小，而船舶动力系统的能量消耗因推进器抵消的推力增大而大幅度增加，从而造成不必要的能量浪费，如图6所示。故偏值量的设定并非越大越好，应结合实际工况合理选取。

图6 推进系统能量消耗对比

图7 推进器1推力变化

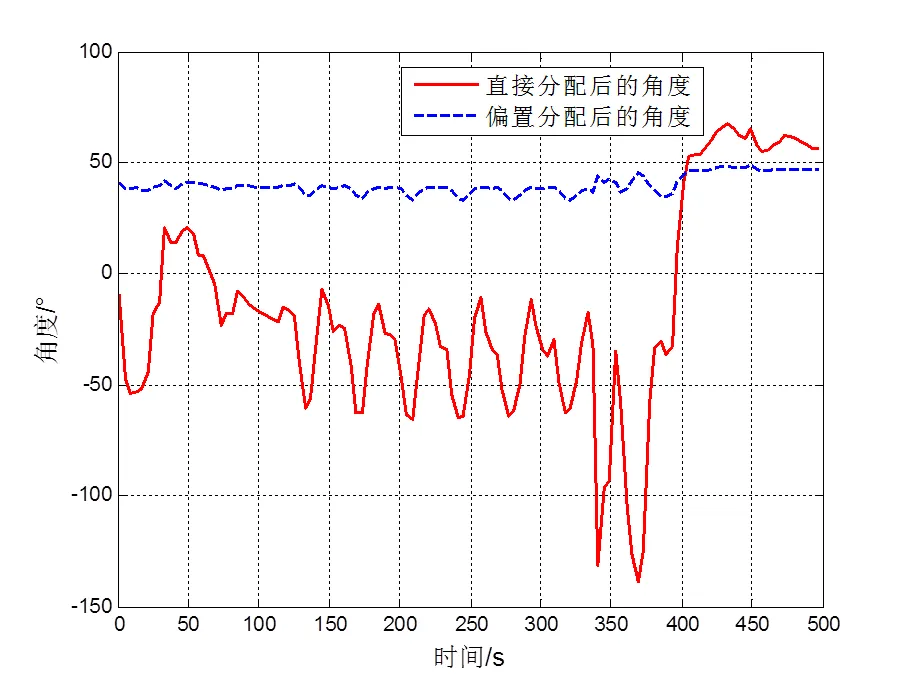
图8 推进器1方位角变化

为了检验组合偏置后进行二次推力分配方法的有效性，取偏置量系数ε=0.2时计算得到的组合偏置后各推进器的方位角，并采用二次推力分配方法计算当前方位角下各推进器的最优推力。图7和图8表示推进器1在不同分配策略下推力和方位角的变化曲线，图9表示推进系统在不同分配策略下能量消耗的变化曲线。从图7可以看出，二次推力分配后的推力比二次推力分配前的推力有较大幅度的减小。从图9可以看出，二次推力分配后推进系统的能量消耗比二次推力分配前有大幅度的降低。因此，在组合偏置后采用二次推力分配方法不仅可以保留组合偏置的优点，使推进器方位角的变化趋于平稳，减小推进器之间的水动力干扰，而且有效地降低了组合偏置后推进器的能量消耗，避免了不必要的能量浪费。

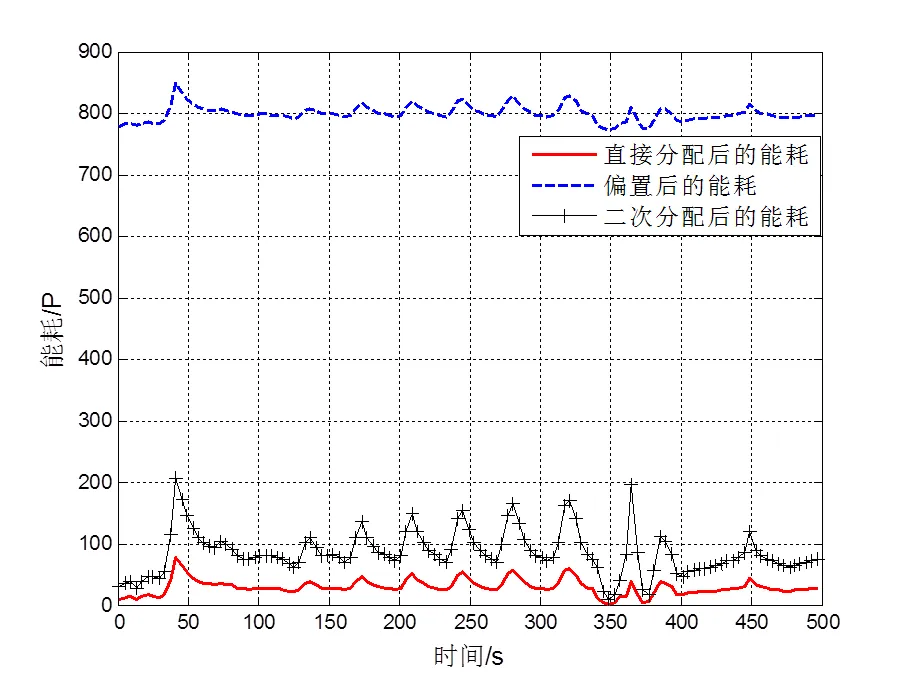
图9 推进系统能量消耗对比

4 结论

组合偏置策略在DP船舶作业中有重要的工程应用价值。本文以一艘DP船舶为仿真实验对象，系统研究了组合偏置中偏置量大小对偏置效果的影响规律，并以减小组合偏置后动力系统能耗为目的，提出了二次推力分配方法。仿真结果表明，随着偏置量的增大，推进器发出的推力也增大，而推进器方位角的变化越平稳，但当偏值量增加到某一临界值时继续增加偏值量对推力分配效果影响很小，却会因推进器抵消的推力增大而大幅度增加推进系统的能量消耗，从而造成大量的能量浪费；组合偏置后采用二次推力分配方法不仅可以使推进器方位角的变化趋于平稳，减小推进器之间的水动力干扰，而且能有效地降低组合偏置后动力系统的燃油消耗，减少大气排放。

[1] 边信黔, 付明玉, 王元慧. 船舶动力定位系统[M]. 科学出版社, 2011.

[2] Christlaan. Optimal thrust allocation methods for dynamic positioning of ships[D], Delft University of Technology, 2009.

[3] Fossen, Johansen. A survey of control allocation methods for ships and underwater vehicles[C]. 14th IEEE Mediterranean Conference on Control and Automation, Ancona, 2006: 1-6.

[4] Kongsberg Maritime AS. Product description kong-sberg k-pos DP dynamic positioning system[M].2006: 96-104.

[5] Veksler, Johansen. Thrust allocation with power management functionality on dynamically positioned vessels[C]. 2012 American Control Conference, 2012: 1469-1475.

[6] 施小成, 魏玉石, 宁继鹏等. 基于能量最优的组合偏置推力分配算法研究[J]. 中国造船, 2012, 53(2): 96-103.

[7] 王芳, 潘再生, 万磊等. 深水钻井平台动力定位的推力分配研究[J]. 船舶力学, 2013, 17(1-2): 19-28.

[8] 徐海祥, 文武, 冯辉. 自适应组合偏置推力分配算法[J]. 武汉理工大学学报(交通科学与工程版), 2016, 40(4): 569-570.

Research on Optimal Thrust Distribution of Dynamic Positioning Ship

Liu Kai, Wen Wu, Xia Yi

(Wuhan Institute of Marine Electric Propulsion, Wuhan 430064, China)

TP273

A

1003-4862（2018）09-0039-05

2018-4-19

文武（1993-），男，硕士。研究方向：船舶动力定位系统。Email: ww199305058@163.com