基于改良C-W节约算法的甩挂运输车辆调度模型

张 笛 钟 明 陈 龙 梁 军 葛慧敏 谈建祥

1.江苏大学汽车工程研究院，镇江，212000

2.江苏省镇江市公安局交通警察支队交通指挥控制中心，镇江，212000

3.镇江兴港国际物流有限公司，镇江，212000

0 引言

甩挂运输集汽车列车运输与装卸甩挂作业技术于一体，是一种集约、高效的运输组织模式，是道路货运业组织化、规模化、网络化、信息化和标准化发展水平的集中体现，在提高运输效率、降低运输成本、促进节能减排等方面具有非常显著的优势［1］。甩挂运输车辆调度问题一直是领域内的研究热点。

为了解决车辆调度中装货和卸货时挂车运输交换问题，王莹［2］提出了一种基于半挂车运输节点之间装卸调度算法模型；CHENG等［3］建立了甩挂分离模式下的集装箱车辆调度数学模型；朱晓兰等［4］提出了针对装配企业采购物流的C-W（Clarke-Wright）节约算法，并在线路规划中插入车辆载重量和容积的双重约束条件；马建华等［5］采用C-W节约算法求解了线路规划可能存在的交叉路径、增加运输里程等情况，并对连接点选择问题进行了优化；潘立军等［6］提出了三类带时间窗约束的车辆调度模型。

本文结合甩挂运输物流的特性，增加了车辆载重和时间窗的约束条件，建立了基于不同载重油耗模型的甩挂运输物流配送模型以及改良的CW节约算法，并以镇江兴港国际物流有限公司为例，验证了改良C-W节约算法的实用性。

1 问题描述

某车辆调度中心拥有装载量为Qk（k=1，2，…，m）的汽车列车，在不同的客户点有若干辆半挂车的运输任务，已知客户点i的货运量为qi（i=1，2，…，n），且qi≥ 0，Qk≥ 0，k∈ K,i∈ C,K为所有牵引车的集合，C为所有客户的集合。求满足货运要求的费用最少的车辆行驶路线。

相关参数假设如下：Eij为运输车从客户i到客户j的运输成本；tij为牵引车从客户i到客户j的行车时间；tsi为牵引车在客户i处的停留时间；T0K为牵引车K的出发时间；TBK为牵引车K的要求返回时间；TEi为客户i允许的最早开始时间；TLi为客户i允许的最迟结束时间；Pk(t0i)为惩罚函数，用来表示车辆到达客户i的时间迟于客户i的最迟结束时间对应的惩罚成本；t0i为车辆从调度中心或车场到达客户点i的时间。

另外，变量xijk和yik的值为0或1。若牵引车K为客户i服务，则yik为1，否则为0，即yik={0,1}，yik表示牵引车分配方案可用布尔矩阵表示；若牵引车 k经由客户 i到客户 j，则 xijk为 1，否则为 0，即xijk={0,1}，xijk表示牵引车路线安排。

为使成本最小以及考虑配送的实际情况，模型同时满足以下约束条件［7］：①甩挂运输中牵引车甩挂的是半挂车，而不是零担货物；②装卸时间只与挂车的数量有关，且在运输网络中的甩挂是没有时间延迟的；③甩挂运输的效率只与汽车列车总的行驶时间和半挂车的装卸停歇时间有关，与半挂车的数量及货物的体积、质量无关；④所有牵引车路线均起始并终止于调度中心，一辆车可以服务多个客户点；⑤每个客户点都有一个非负的货物需求量；⑥满载时，需要运输的挂车数量等于一辆汽车列车允许装载的最大半挂车数量的整数倍，完成所有任务要多辆运输车辆；非满载时，需要运输的挂车数量少于一辆汽车列车允许装载的半挂车数量，完成任务只需要一辆运输车辆。

2 成本模型建立

运输过程中的汽车油耗成本是运输成本的一个重要组成部分，燃油的消耗量受到车辆状况、行车速度、行驶里程、车辆载重、驾驶习惯、道路状况，油品质量以及天气状况等多种因素的影响，本文探讨的油耗成本模型只考虑行驶里程和车辆载重（挂车的数量），在计算满载和非满载等情况下认为风阻力不变（行车速度不变），汽车的机械传动损失不变，路面情况不变，路面的摩擦损失与压力成正比，油耗和牵引车加挂车的质量之和成正比。这里给出不同载重和不同行驶距离下的车辆油耗模型：

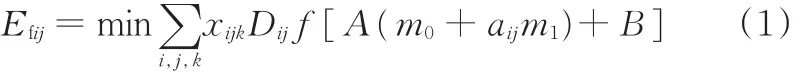
式中，Efij为运输车从客户i到客户j的油耗成本；Dij为客户点i和客户点j之间的地理距离，百公里；f为每升燃油的价格，元；A为油耗和载重的正相关系数；B为常数；m0为牵引车的质量，t；m1为挂车的质量，t；aij为需要从客户点i运输到客户点j的挂车数量，辆。

过路费成本是指车辆通过高速公路需要的过路费，主要和车辆行驶的距离有关，此成本模型为

式中，Erij为运输车从客户i到客户j的过路费成本；H为车辆每行驶百公里的过路费用。

装卸停歇时间成本是指牵引车在客户处装卸挂车所产生的时间成本，这一成本只和装卸挂车的数量相关，此成本模型为

式中，Esij为运输车从客户i到客户j的装卸停歇时间成本；D为一辆挂车装载或者卸载所需要的时间成本。

配送延迟成本Epi指车辆没在规定的时间内到达客户处所需要支付的罚金。此成本模型为

综上所述，带有时间窗的甩挂运输车辆配送优化模型及约束条件如下：

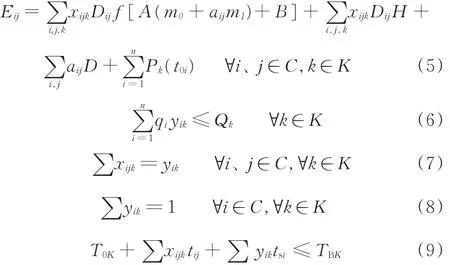
其中，式（5）为目标函数；式（6）表示一条线路上客户需求总量不超过车辆的最大载重量；式（7）、式（8）表示每个客户点只能由一辆车服务，且这些客户点是在一条服务路线上；式（9）表示每辆牵引车的行车路线总耗时不超过预先确定的数值，即每辆牵引车需要在规定时间内返回配送中心；式（10）表示对某个客户点，牵引车到达时间限制在某一时间段内。

3 算法求解

C-W节约算法是由Clarke和Wright于1964年首次提出的，起初是为解决旅行商问题，因此它不考虑各种约束条件，故无法直接用来求解车辆路径问题（vehicle road problem，VRP），但可以通过加入检验车辆载重约束和时间窗约束来完善CW节约算法，使之能够求解单类型车辆路径问题［8］。

在初始路径0-i-0中，Ef0i是汽车从调度中心或者车场去往客户点i过程中产生的油耗成本，Efi0是车辆由客户点i返回调度中心过程中所产生的油耗成本，虽然来回过程的运输距离是一样的，但由于载重量不同，所以Ef0i和Efi0不相等。过路费成本只和运输距离成正相关关系。装卸停歇时间成本由于每次装卸的时间是固定的，因此只和每个客户点需要装卸的半挂车数量相关。配送延迟成本需要结合具体情况分析。

用改良节约算法解决该问题的步骤如下：

（1）首先计算客户i和客户j之间线路的费用节约值s(i,j)，形成集合N，并按照从大到小对s(i,j)进行排序，s(i,j)分为油耗费用节约值sf(i,j)和过路费用节约值sr(i,j)，即s(i,j)=sf(i,j)+sr(i,j),而

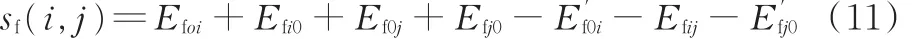
其中，Ef0j为在初始路径0-j-0中汽车从调度中心或者车场去往客户点j过程中产生的油耗成本；Efj0是车辆由客户点j回调度中心过程中所产生的油耗成本。在调度后的路径0-i-j-0中，为汽车从调度中心到客户点i过程中所产生的油耗成本；Efij为从客户点i到客户点j的油耗成本为客户点j回到调度中心的过程中产生的油耗成本。但由于车辆从j点返回配送中心时，车辆都处于空载状态，所以Efj0=，因此：

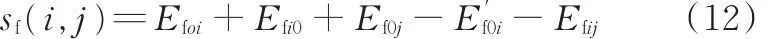
再将油耗成本模型公式代入式（12），得

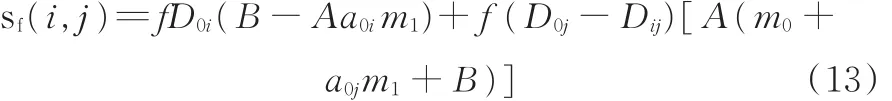
式中，D0i、D0j分别为调度中心和客户点i、j的地理距离；a0i和a0j分别为调度中心运输到客户点i和j的挂车数量。

过路费用节约值

式中，Eroi、Erj0分别为车辆路径0-i和j-0的过路费成本。

将过路费成本模型公式代入式（14），得式

中，Dj0为车辆从客户点j到调度中心的距离。

综上可得

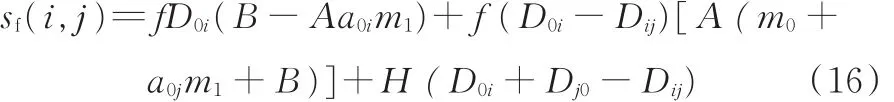
（2）若N为空，则终止叠代，否则考察N中的第一项s(i,j)是否满足下列条件之一：①点i和j均不在已构成的线路上；②点i和j在已构成的线路上，但不与车辆调度中心相连；③点i和j位于已构成的不同线路上，且均不与车辆调度中心相连，一个是起点，一个是终点。如满足此条件则转步骤（3），否则转步骤（6）。

（4）计算连接点i和j所在的线路后，车辆到达j点的时间比原路线上车辆到达j点的时间的变化量为：Δtj=t0i+tsi+tij-t0j。t0i为车辆从调度中心或者车场到达客户点i的时间，t0j为车辆从调度中心或者车场到达客户点j的时间。①若Δtj=0，则转步骤（5）；②若Δtj＜0，则计算∆j-，当Δtj≤ ∆j-时，转步骤（5），否则转步骤（6）；③若Δtj＞0，则计算∆j+，当Δtj≤∆j+时，转步骤（5），否则转步骤（6）。其中，∆j-为线路上j点后面的各个客户处均不需要等待的到达j点时间的最大允许提前量；∆j+为线路上j点后面的各个客户不违反时间约束的到达j点时间的最大允许推迟量。

（5）连接点i和点j，计算牵引车到达各个客户点时的新时间。

（6）令N=N-s(i,j)，转步骤（2）。

以上是针对单个车辆调度中心的车辆优化调度问题的求解，多调度中心的车辆调度问题可以转化为单个调度中心问题来处理，首先确定每个调度中心需完成的任务，然后再求解多个调度中心的车辆调度问题。

4 应用研究

如图1所示，地点A是镇江兴港国际物流有限公司的配送中心，地点1～9是主要装卸点。根据调查，得到各装卸点之间的距离以及各个装卸点与配送中心之间的距离，见图1。

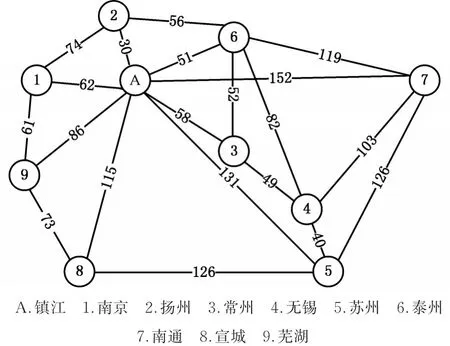
图1 配送中心与装卸点之间的分布示意图（km）Fig.1 Distribution center and the distance between the loading and unloading point diagram（km）

据英国交通部对车辆油耗与载重间关系的研究数据可知［9］，车辆的油耗与载重间存在较强的线性正相关特性，可以简化为线性关系：

式中，F为每百公里油耗成本；M为整车质量。

一般情况下，牵引车会使用0号柴油，价格为6.36元/L，定义牵引车的质量为10 t，每辆挂车的质量为15 t，车辆的过路费为160元/百公里，每辆半挂车平均装卸停歇时间为0.6 h，时间成本40元/h，牵引车的时间惩罚系数为0.6，每辆牵引车最多可拖带4辆挂车，牵引车的平均速度为80 km/h，所允许最长的运输总时间为6 h。

车辆调度开始前，各个装卸点需运输的挂车数量如表1所示。

表1 各个装卸点需运输的挂车数量Tab.1 The number of trailers to be transported at each loading and unloading point

运用上文的甩挂运输调度算法对这次车辆调度进行优化。进行初步调度需要牵引车的数量如表2所示，调度后各个装卸点剩余挂车数量如表3所示，费用节约值如表4所示。

根据改良的节约算法对所需牵引车进行调度的行驶路线如图2所示。

表2 初步调度需要的牵引车数Tab.2 The number of truckers required after initial dispatch

表3 调度后各个装卸点剩余的挂车数量Tab.3 Number of trailers remaining at each loading point after dispatch

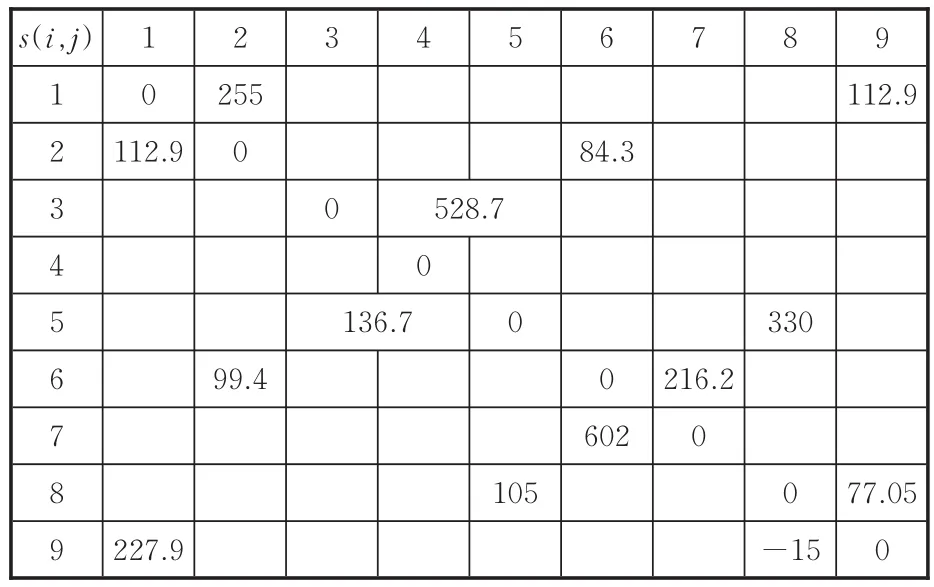
表4 费用节约值（元）Tab.4 The cost savings（￥）

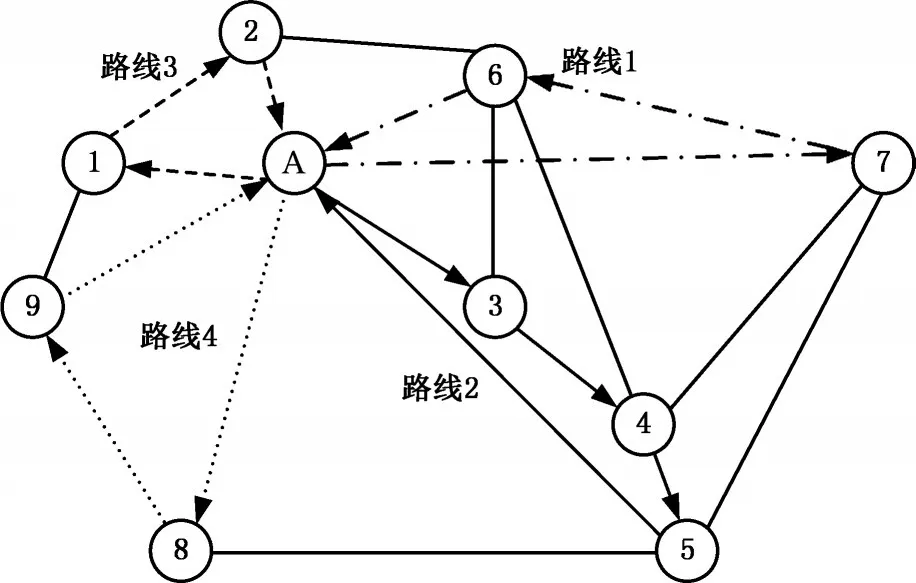
图2 调度路线示意图（km）Fig.2 Scheduling route diagram（km）

初步调度后不使用调度算法运送货物至各个装卸点的成本表如表5所示。各个装卸点的运输总成本为5 850.34元。通过改良的节约算法再次调度各个线路的费用节约值如下。

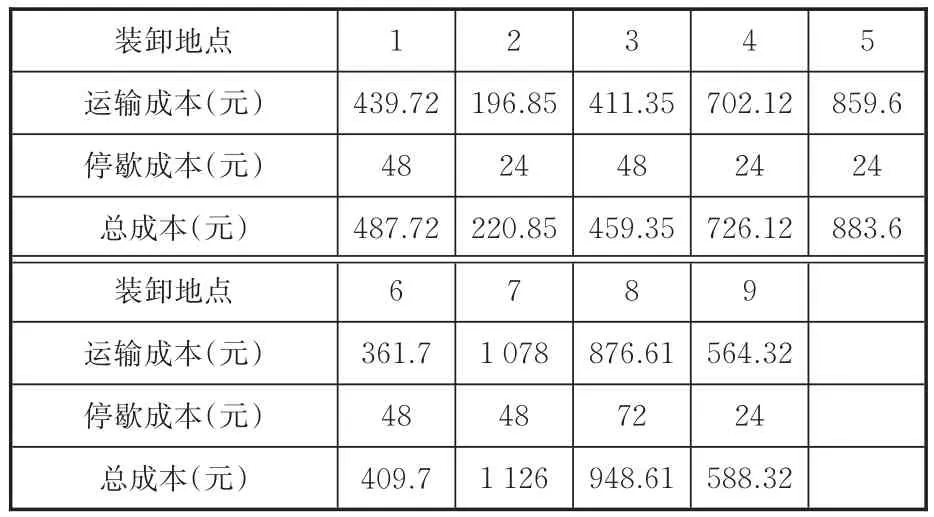
表5 原装卸成本Tab.5 Original shipping and delivery cost

线路1（A-7-6-A）的费用节约值为602.3元，时间为4.025 h；线路2（A-3-4-5-A）的费用节约值为528.7元，时间为3.475 h；线路3（A-1-2-A）的费用节约值为255.3元，时间为2.075 h；线路4（A-8-9-A）的费用节约值为77元，时间为3.425 h；各条路线的费用节约总值为1 463.3元。使用改良节约算法进行车辆调度运输总成本减少了1 463.3元，降低了25.01%。

算例证明本文所创建的节约算法可以降低甩挂运输的运输成本，并且有效地解决了运输过程中的车辆调度问题。

5 结论

本文基于不同载重下的油耗模型以甩挂运输车辆最优运输路径为研究对象建立了一种改良型C-W节约算法，构建了基于油耗模型的甩挂运输物流配送优化路径模型，模型以包括油耗成本、过路费成本、装卸停歇时间成本以及延时惩罚成本在内的总成本最小为目标函数，以车辆载重和时间窗作为约束。在算法上，构建了改良型的C-W节约算法，并用该算法找出了一个9客户算例的最优路径。最后通过在算例中比较调度前后的运输成本，证明了节约算法可以降低甩挂运输的运输成本，从而得出建立基于不同载重油耗模型的甩挂运输物流配送路径优化模型的必要性。