一种考虑参数相关性的可靠性优化设计方法

王倩蓉 姜 潮 方 腾

湖南大学汽车车身先进设计制造国家重点实验室，长沙，410082

0 引言

在工程问题中，加工尺寸、外载荷、材料参数等往往存在不确定性，在设计时若不考虑这些不确定性，可能得到不可靠的设计结果［1］。基于可靠性的优化设计（reliability-based design optimization，RBDO）充分考虑了各种不确定性，将不确定性变量作为随机变量来处理，从而可以得到满足可靠性要求的设计结果。目前，RBDO已经成为一种十分重要的设计方法，且该领域已发展出一系列求解方法。ZHUANG等［2］在求解RBDO问题中不断更新响应面，保证了收敛性和精度；LIANG等［3］提出了单循环方法，采用K-K-T条件取代内层的可靠性分析问题，将两层的优化问题转换成单循环问题；YI等［4］将序列近似规划策略应用到RBDO中，通过构建并求解一系列近似规划子问题来获得RBDO问题的解；DU等［5］提出了SORA（sequential optimization and reliability assessment）方法，通过运用上一循环的可靠性分析信息构造漂移向量，将RBDO问题转换成一系列确定性的优化问题，有效地提高了计算效率，同时具有较高的计算精度并能保证收敛性。

现有的RBDO方法大多假设各随机变量相互独立，然而，在实际工程问题中，很多变量之间具有显著的相关性。现有研究表明，变量之间的相关性对结构的可靠性和优化结果可能产生十分显著的影响［6］。在RBDO问题中充分考虑变量间的相关性，可进一步提高优化模型的准确性，并避免产生不可靠的优化结果。目前，Nataf变换是处理随机变量相关性的主要方法，已被应用于RBDO领域。CHENG 等［7］利用Nataf变换求解RBDO问题。DU等［8］提出了一种考虑相关区间变量的RBDO方法。Nataf变换仅能描述变量之间的线性相关性，对于一些实际问题中广泛存在的非线性相关性，应用Nataf变换可能会出现比较大的误差，这使得Nataf变换的应用范围受到了限制。

近年来，在不确定性分析领域发展出了一种处理相关性的重要数学工具——Copula函数。通过Copula函数，只需确定变量的边缘分布和相关类型，即可方便地构建出联合概率分布函数。此外，Copula函数可描述变量之间不同类型的非线性相关性，并能捕捉到一些重要的信息，如尾部相关性等，这使得Copula函数近年来被广泛用于解决结构可靠性分析问题［9-10］。虽然Copula函数在可靠性分析方面引起了重视，但将其应用到RBDO领域的相关工作仍很少。CHOI等［11-12］利用Copula函数构建联合概率分布函数，并首次将Copula函数用于求解RBDO问题。然而，上述工作只使用了Copula函数的一种类型，即Gaussian Copula函数来描述变量间的相关性。在本质上，Gaussian Copula函数与Nataf变换是等效的，仅能描述变量间的线性相关性［13］。若能根据样本的实际分布情况选择出描述变量之间相关类型的最优Copula函数，则可更加准确地建立数学模型，进一步提高不确定性分析精度。

本文提出了一种基于Copula函数的RBDO方法，为存在复杂参数相关性的结构可靠性优化问题提供了一种有效工具。

1 Copula函数基本原理

SKLAR［14］指出，任一联合概率分布函数都可被分解为若干个边缘分布和一个Copula函数，该Copula函数可描述变量之间的相关性。由此看出，Copula函数实际上是一种将多个变量x1,x2,…,xn的联合概率分布函数F(x1,x2,…,xn)与它们各自的边缘分布函数F1(x1),F2(x2),…,Fn(xn)连接在一起的函数。根据Sklar定理可知，联合概率分布函数与各边缘分布函数之间满足：

C即为描述F1(x1),F2(x2),…,Fn(xn)之间相关性的Copula函数。令uk=Fk(xk),k=1,2,…,n，显然，C(u1,u2,…,un)是一个边缘分布均服从[0,1]均匀分布的多元分布函数。

若已知各变量的边缘分布和连接它们的Copula函数，则可根据Sklar定理求解出联合概率分布函数。联合概率分布函数的概率密度

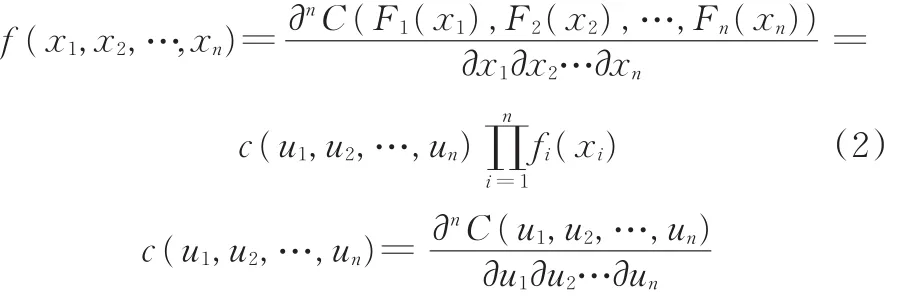
1.1 Copula函数的相关性测度

两个变量之间，若它们的变化趋势一致，则称这两个变量正相关，反之则称负相关。由此可定义一致性的概念：(x1,y1)和(x2,y2)为(X,Y)的两组观测值，若 (x1-x2)(y1-y2)＞ 0，称(x1,y1)和(x2,y2)是一致的；若(x1-x2)(y1-y2)＜ 0，则称(x1,y1)和(x2,y2)是不一致的。HOLLANDER等［15］基于一致性的概念提出了Kendall秩相关系数的定义。假设对连续的随机向量(X,Y)进行观测，得到一个由N组观测值组成的样本集{(x1,y1),(x2,y2),…,(xN,yN)}；将这些观测值两两匹配，得到C2N项组合，并将其分为两部分，即C2N=c+d，c表示一致组合的数量，d表示不一致组合的数量，由此可定义样本{(x1,y1),(x2,y2),…,(xN,yN)}的 Kendall秩相关系数：

若给定一个Copula函数，则变量之间的相关性也随之确定。Kendall秩相关系数τ可由相应的Copula函数C( )u1,u2根据下式计算［16-17］：

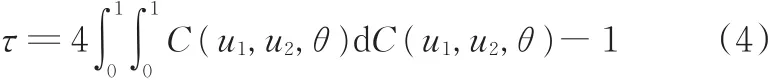
式中，θ为该Copula函数的相关性参数。

式（4）中不含随机变量边缘分布的表达式，这也表明了对于某个Copula函数，其Kendall秩相关系数不依赖于边缘分布。

在实际工程问题中，变量之间广泛地存在着尾部相关性。由于Kendall秩相关系数τ和Pearson相关系数（即线性相关系数ρ）都无法描述尾部相关性，因此引入尾部相关系数。若X1、X2为两个连续型随机变量，其边缘分布分别为F1(X1)、F2(X2)，用Copula函数表示其联合概率分布函数为C(F1(X1),F2(X2))，其尾部相关系数［18］可由下式定义：

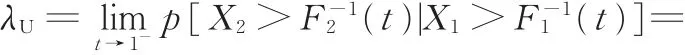
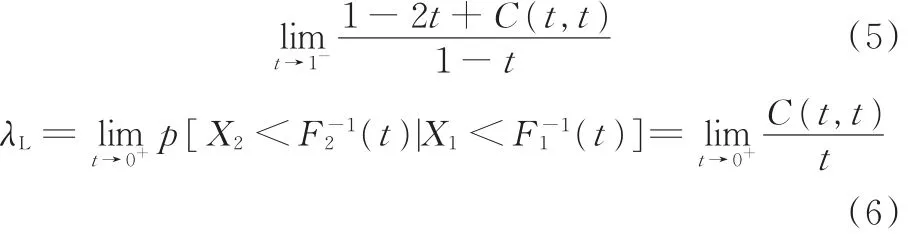
式中，λU为上尾相关系数；λL为下尾相关系数；p为事件发生的概率；F-12为边缘分布F2的逆函数；t→1-表示t无限趋近于1的左侧。

尾部相关系数可用来表示当一个变量为极值时，另一个变量也出现极值的可能性。尾部相关性可能对结构的可靠性造成显著的影响［9-10］，因此，在RBDO问题中考虑尾部相关性可提高优化的精度。

1.2 常用的二维Copula函数分类

为方便起见，在本文中，仅考虑二维相关的情形，即多维随机变量中仅有两个变量之间具有相关性。当有两个以上的变量之间两两相关时，可利用Vine-Copula函数将多维Copula函数分解成若干个二维Copula函数。

目前常用的二维Copula函数见表1，分别为Gaussian Copula（可等效为Nataf变换）、t Copula、Clayton Copula、Gumbel Copula和Frank Copula。表1公式中，u1、u2为变量名称，tν和Φ分别表示t分布和高斯分布函数。为了更直观地理解各Copula函数的性质，图1给出了在秩相关系数相同（τ=0.5）、边缘分布均为标准正态分布、仿真次数均为2 000的情况下，由5种不同的Copula函数仿真得到的随机变量的散点图。从图1中可以看出，即使具有相同的秩相关系数和相同的边缘分布（标准正态分布），两个随机变量也可呈现不同的相关模式。例如，Gaussian Copula、t Copula和 Frank Copula的分布具有对称性，且t Copula具有明显的尾部相关性。Gumbel Copula和Clayton Copula能描述非对称的相关模式，其中前者具有明显的上尾相关性，而后者则有明显的下尾相关性。可以看到，Copula函数能够描述变量之间不同的非线性相关类型。通过Copula函数，可更准确地建立随机变量联合概率分布函数。

表1 常用的二维Copula函数信息［10］Tab.1 General information of two-dimension Copula function

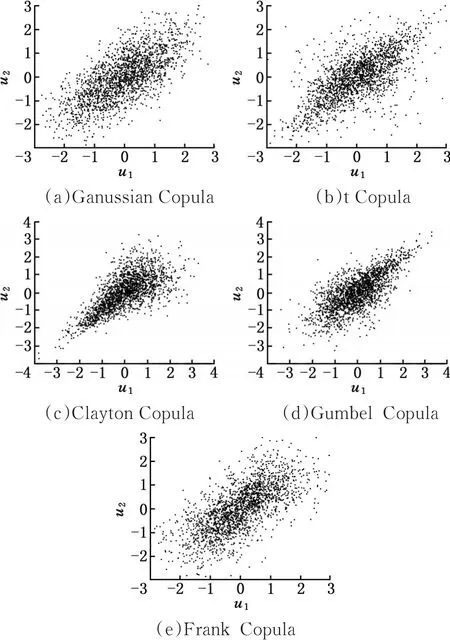
图1 各Copula函数仿真散点图Fig.1 Simulation scatter diagram of Copula functions

2 基于Copula函数的RBDO求解算法

RBDO问题通常可表述如下［3］：

式中，f为目标函数；gi为第i个可靠性约束；m为约束总个数；d为nd维确定性设计向量；X为nX维随机向量；μX为X的均值向量；P为nP维随机参数向量；、分别为设计变量dj的下界和上界、分别为μXp的下界和上界；Φ为标准正态分布累积分布函数；βti为第i个约束的目标可靠度。

2.1 联合概率分布函数的构建

在求解RBDO的过程中，当变量具有相关性时，需要利用联合概率分布函数进行求解。在实际工程问题中，通常只能获得各变量的边缘分布函数。Sklar定理指出，联合概率分布函数可被分解成边缘分布函数和一个描述变量之间相关性的Copula函数，这提供了一种构建联合概率分布函数的思路：分别获得随机变量的边缘分布及连接两边缘分布的Copula函数，从而得到联合概率分布函数F(x1,x2,…,xn)。

本文将 Gaussian Copula、t Copula、Clayton Copula、Gumbel Copula和Frank Copula作为备选Copula函数，基于已知样本，通过极大似然法对这5种Copula函数进行参数估计，再由AIC（akaike information criterion）信息准则［19］选择出拟合效果最好的Copula函数，确定出变量之间的相关类型。若随机变量X1、X2的边缘累积分布函数分别为F1(X1),F2(X2)，已知样本集合为{(x11,x21),(x12,x22),…,(x1l,x2l)}，共l组样本。对备选Copula函数建立似然对数函数：

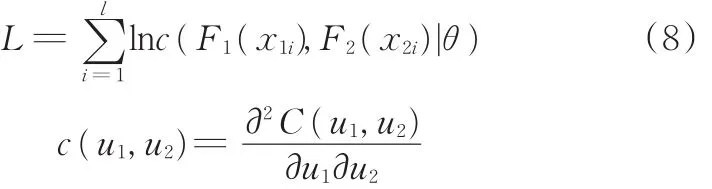
式中，θ为备选Copula函数的相关性参数（t Copula有两个参数：θ和ν）。

由极大似然原理，参数估计值

对5种备选函数均使用极大似然法求得其参数的估计值后，可用AIC准则或BIC准则择取最优Copula函数：

式中，r为相应Copula函数中参数的数目。

CAIC值越小，说明该Copula函数对样本拟合越准确。由Sklar定理可知，当变量之间的Copula函数确定后，其联合概率分布函数也随之确定。

2.2 约束可靠性分析

约束可靠性分析是求解RBDO问题中的重要环节，用于分析当前设计变量d和μX是否满足概率约束。第i个约束gi的失效概率

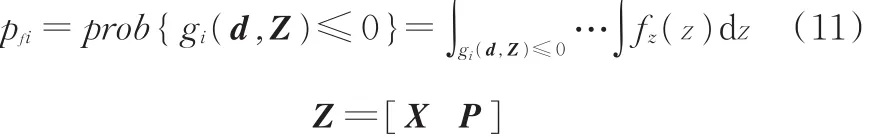
式中，fz(Z)为联合概率密度函数;prob表示事件发生的可能性。

一次二阶矩法（first-order reliability method，FORM）［20］是进行可靠性分析常用的一种高效方法。该方法需将原功能函数gi从Z空间映射至标准正态空间（即U空间），得到功能函数Gi，并求解如下优化问题：

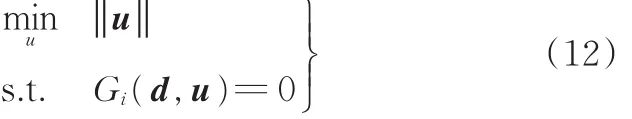
其中，u表示待优化的随机变量和随机参数。

该优化问题的解为u∗即最可能失效点（most probable point，MPP），进而可得到第i个约束的可靠度指标 βi=‖u∗‖ 。若 βi≥ βti，则说明概率约束满足要求，反之则不满足。由于该方法用可靠度指标β来度量可靠性，故也称为可靠度指标法（reliability index analysis，RIA）。

此外，在FORM方法中还有另一种可靠性分析方法——功能度量法（performance measure approach，PMA），该方法同样可以表述为一个优化问题：

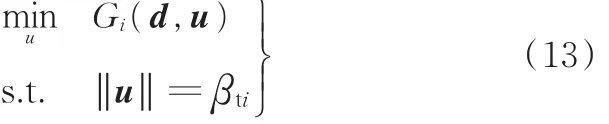
该优化问题的解u∗即为MPP点。若Gi(d,u∗)≥0，则说明满足概率约束，反之则说明不满足。将u∗从U空间映射回Z空间后，记为ZMPPi。对于RBDO问题，在大多数情况下，PMA法相对于RIA法效率更高、稳定性更好，且较少依赖于随机变量的分布类型。

在使用RIA法或PMA法进行可靠性分析时，需要将约束从Z空间映射至U空间，当变量之间存在相关性时，需要用Rosenblatt变换进行全概率变换。对于二维问题，Rosenblatt变换和逆变换如下：

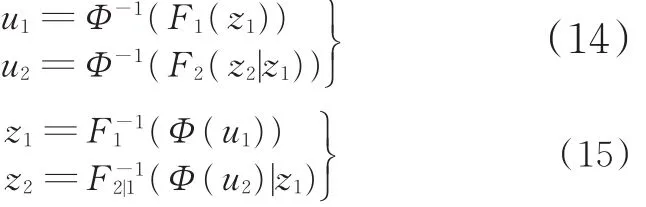
式中，F1(z1)为z1的边缘累积分布函数；F2|1(z2|z1)为Z1=z1时Z2的条件分布函数。

求解条件分布函数需要先得到联合概率分布函数，而在实际工程问题中，通常不能准确地得到联合概率分布函数，这使得Rosenblatt变换的应用受到了限制。通过2.1节中提出的方法可利用Copula函数方便地得到条件分布函数：

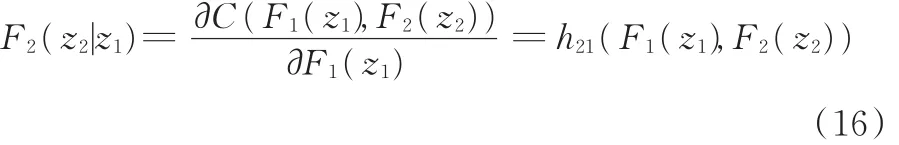
将Z空间的点(z1,z2)转换至U空间的点(u1,u2)的变换步骤为：令r1=F1(z1)，r2=F2(z2)；令y1=r1，可得u1=(y1)；由y2=F2(z2|z1)=，可 得 y2=(y1,r2)；从而有u2= Φ-1(y2)。

需要指出的是，对于Gumbel Copula，h-121没有显式的表达式，此时可求解非线性方程h21(r1,r2)=y2得到数值解。

2.3 设计变量的优化

RBDO本质上是个两层嵌套优化问题，其外层是设计变量的优化，内层为约束可靠性的分析。嵌套优化使得RBDO求解效率较低，尤其是当随机变量的个数增加时，所需的计算量显著增大。为减小运算量，本文在文献［5］的基础上，构建了一种解耦算法，对含有非线性相关性的结构可靠性优化设计问题进行高效求解。该方法由若干个迭代步组成，在每个迭代步中，首先对各约束进行可靠性分析，利用MPP点构造一漂移向量，将原问题转换为等效的确定性优化问题，通过求解该问题更新设计变量。由此，将嵌套优化解耦成序列进行的可靠性分析和确定性优化问题。在第k次迭代中，原问题被转化成如下形式：

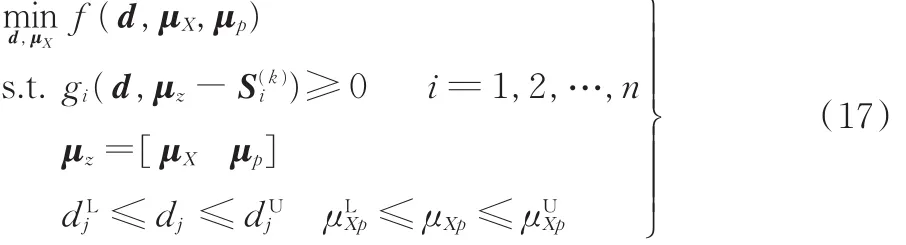
其中，μp表示随机参数向量的均值，漂移向量可通过下式求得：

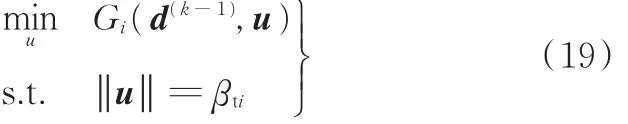
综上所述，本文RBDO方法的计算流程如下。

（1）根据实际情况构造如式（4）形式的RBDO问题。

（2）根据已知样本对随机变量进行相关性分析，对存在相关性的变量利用极大似然法求得估计参数值。

（3）利用AIC准则求出拟合度最佳的Copula函数，从而求得联合概率分布函数。

（4）令k=1，给定设计变量的初值d(0)、（可用确定性优化结果作为迭代的初值，从而加快收敛，减小计算量）。

（5）在第k次迭代中，利用Rosenblatt变换将每一个约束映射至U空间进行可靠性分析，求解式（19），得到MPP点。

（7）求解确定性优化问题式（17），得到更新后的设计变量d(k)、。

（8）计算

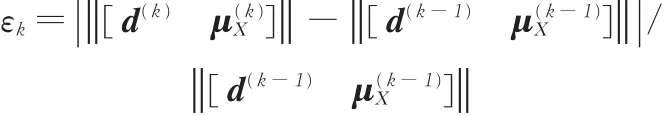
若εk＞ 10-3，判定为不收敛，则k+1→k，转到步骤（5）；若εk≤ 10-3，判定为收敛，则程序终止，得到优化结果[d(k)]。

3 数值算例

3.1 算例一

考虑如下RBDO问题：

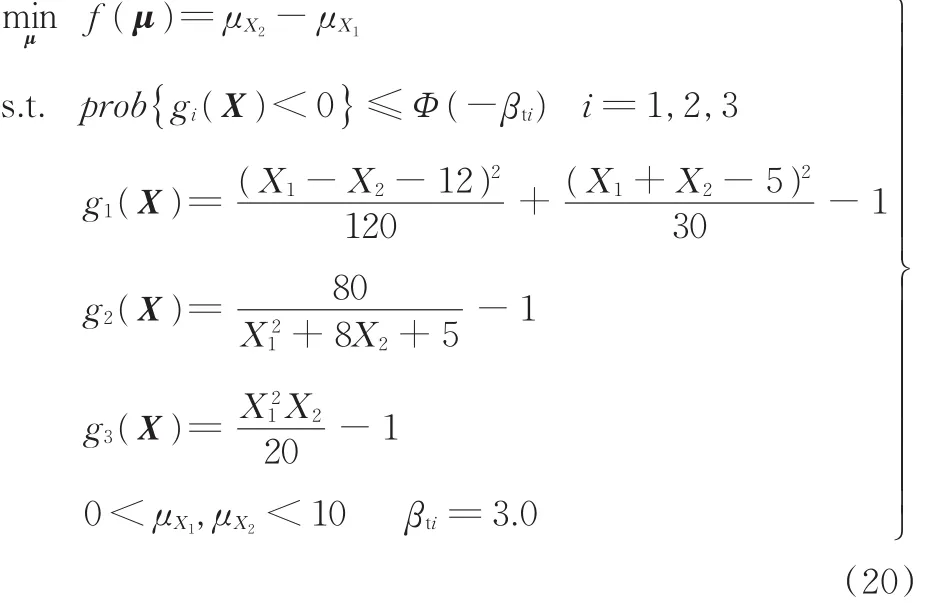
其中，X1～N(μX1,0.52),X2～N(μX2,0.52)，优化的初始点(μX1,μX2)=(0,0)。X1和 X2的 500 组样本见图2，从图中可知X1和X2之间具有明显的相关性。按照2.1节的方法对样本进行参数估计和相关性分析，可以得到各备选Copula函数的参数估计值和AIC值，见表2。从表中可知，用Gumbel Copula拟合样本得到的AIC值是各备选Copula函数中最小的，为最优Copula函数。实际上，从样本的散点图亦可知，该组样本具有明显的上尾相关性，而下尾相关性相对不明显。5种备选Copula函数中，只有Gumbel Copula具有这样的性质，因而其拟合效果也最好。根据参数估计和相关性分析所得到的最优Copula函数及其参数值，即可求解该RBDO问题。

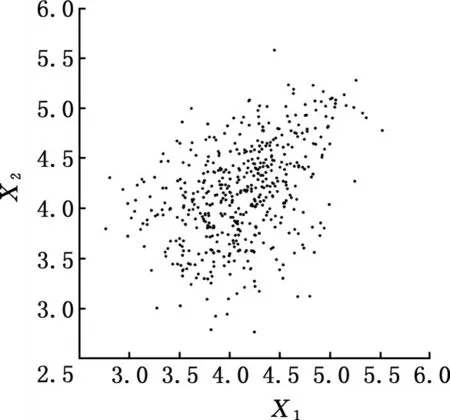
图2 X1和X2的500组样本Fig.2 500 samples of X1，X2

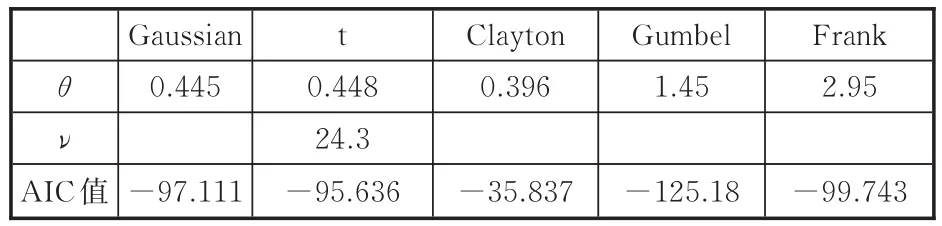
表2 X1、X2之间备选Copula参数估计值及其AIC值Tab.2 Estimate of Copula parameter and AIC value betweenX1、X2

虽然已经得到最优Copula函数，但是为了分析不同类型的Copula函数对于优化结果的影响，本文仍使用3种Copula函数进行RBDO分析：①Gumbel Copula，θ=1.45（最优Copula函数）；②Gaussian Copula，θ=0.445；③Clayton Copula，θ=0.396。如表3所示，优化均经过4个迭代步即达到收敛，说明本文方法具有较好的收敛性和计算效率，但3种相关情形下得到的优化解具有明显的差异。为了解释优化结果产生差异的原因，将3种相关情形下的优化结果和各自的β-circle画在平面直角坐标系中，见图3。β-circle是指在U空间中所有到原点距离为β的点映射至X空间所得点集。在本算例中，X1和X2都为正态分布且标准差σ=0.5。若X1和X2相互独立，则β-circle应该是一个半径R=σβt=1.5的圆；若X1和X2之间存在线性相关性，则β-circle演化成长轴与X轴成45°角的椭圆。当用Copula函数描述变量间的相关性时，β-circle则为其他类型的形状，该形状与Copula函数的种类及其参数有关。在优化过程中，βcircle不与各个约束相交，以保证设计点与约束之间存在安全距离，从而满足可靠性要求。

表3 算例一优化结果Tab.3 Optimization results of example 1

由图3可知，3种相关情形下最优解的β-circle与g1、g2均相切，但由于其形状不同，得到的最优解具有较大差异。这说明对于同一组样本，用不同的Copula函数拟合得到的优化结果具有较大的差异，从而说明选择最优Copula的必要性。此外，由于Gaussian Copula函数可等效为Nataf变换，对比Gaussian Copula函数和Gumbel Copula函数的优化结果，可知在存在复杂相关性的RBDO问题中，若不考虑非线性相关，传统的Nataf变换得到的优化结果可能有较大误差。

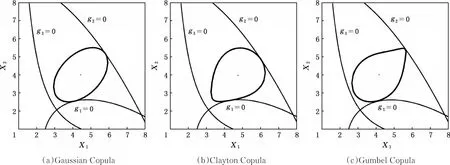
图3 约束与β-circle示意图Fig.3 Illustration of constraint and β-circle

3.2 算例二

考虑一受轴向定载荷的弹簧优化问题［12］，其目标是减小弹簧的总质量。在该算例中，有5个随机变量，分别为弹簧内径D、线径d、有效圈数N、材料密度ρ和材料剪切模量G，均服从正态分布，其中D、d、N是随机设计变量，ρ、G是随机参数，具体参数见表4。该问题有3个可靠性约束：在轴向载荷P=10 lbf（1 lbf=4.448 22 N）作用下（见图4），变形量 δ不小于一给定值 Δ=0.5in（l in≈25.4 mm）；剪切应力不大于许可值τa=80 000lb/in2；弹簧固有频率不小于一给定值ω0=100 Hz。由变形量约束可得

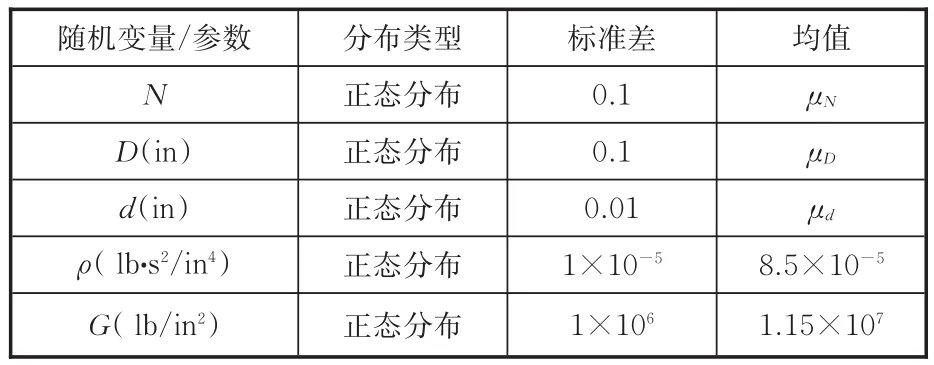
表4 算例二各随机变量/参数信息［12］Tab.4 Random variables/parameters of example 2

图4 弹簧及其受力示意图［18］Fig.4 Illustration of the spring and force diagram

式中，K为劲度系数。

由剪切应力约束可得

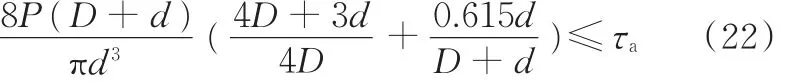
由固有频率约束可得

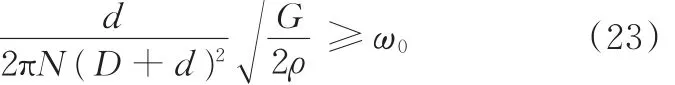
因此，该优化问题可写为如下形式：

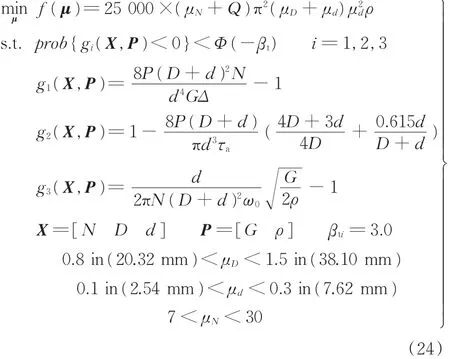
其中，Q为弹簧闭合端圈数，Q=2。已知在实际生产中，平均中径D和丝径d具有相关性，故在求解RBDO问题时需将其考虑进来。D、d的300组样本见图5，对其进行相关性分析，结果见表5。从结果中可知，Clayton Copula的AIC值最小，故D和d之间的最优Copula为Clayton Copula，其参数θ=2.92。若用Gaussian Copula对样本进行拟合，则对应参数θ=0.76。

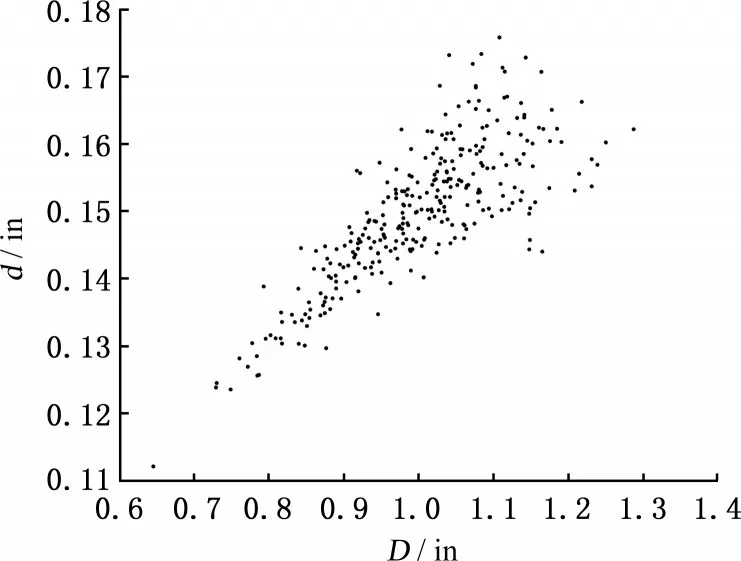
图5D、d的300组样本Fig.5 300 samples of D、d

表5 D、d之间备选Copula参数估计值及其AIC值Tab.5 Estimate of Copula parameter and AIC value betweenD、d

与算例一类似，虽然已经得到最优Copula函数，本文仍在以下3种相关情形下进行RBDO求解：①Clayton Copula，θ=2.92；②Gaussian Copula，θ=0.76；③相互独立。得到的优化结果见表6。从表6中可以看出，变量之间的相关情形对优化的结果影响较大。对于同样的一组样本，用不同的Copula函数拟合将得到不同的优化结果。此外，在3种相关情形下，优化均经过3个迭代步达到收敛，进一步说明了本文方法具有较好的收敛性和计算效率，迭代过程见图6。

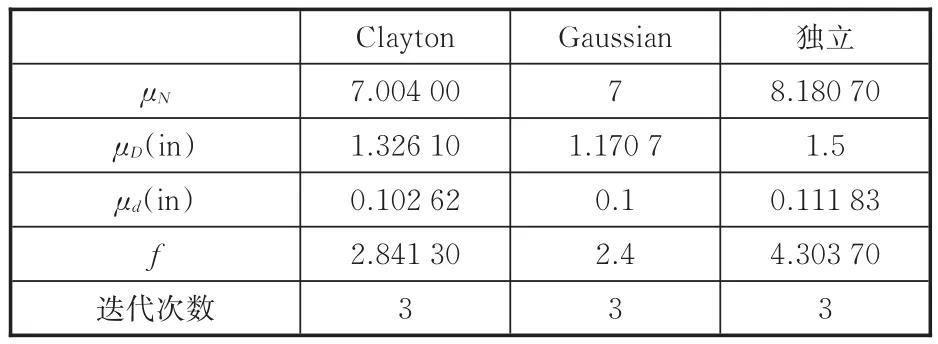
表6 算例二优化结果Tab.6 Optimization results of example 2

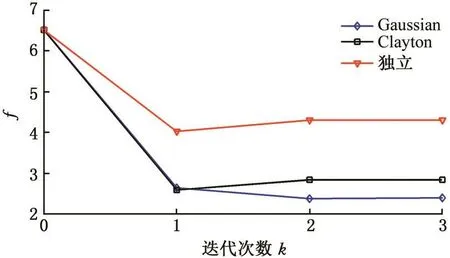
图6 算例2迭代历史Fig.6 Iteration history of example 2

现假设X2和X3之间实际的Copula函数为Clayton Copula，参数θ=2.92，用Monte-Carlo模拟法对3种优化结果进行可靠性验证（即用Monte-Carlo法验证时产生的样本之间的相关类型为Clayton Copula），其可靠度和失效概率见表7。由表7可知：若将X2和X3的样本用Gaussian Copula拟合，得到的优化结果中g1的可靠度β仅为2.330 9，失效概率Pf达到了0.009 9，是目标值（0.001 3）的近8倍，未能满足可靠性；将X2和X3错误地视为独立的随机变量，其优化结果的可靠度远大于目标可靠度，过于保守。前文提到，Gaussian Copula实际上等效为传统的Nataf变换，即只考虑了变量间的线性相关。从该算例中可以看出，仅用线性相关系数对随机变量的相关性进行描述是不足够的，若不考虑随机变量间存在的复杂非线性相关性，可能会得到不可靠的优化结果。将Copula函数引入到RBDO中，通过AIC准则选择出正确的Copula函数能充分考虑到变量间的非线性相关性，提高优化结果的精度。

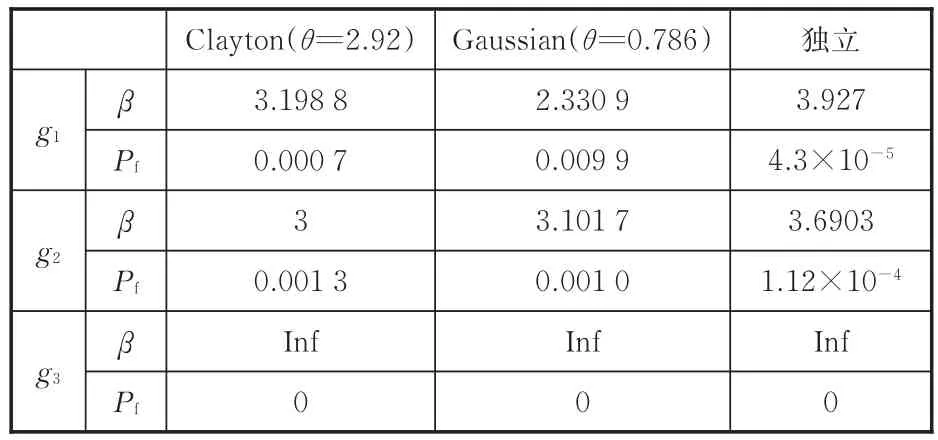
表7 实际相关情形为Clayton Copula时，各优化结果可靠度Tab.7 Reliability of optimization results when the actual correlation is Clayton Copula

4 结论

本文基于Copula函数提出了一种RBDO算法，为求解存在复杂非线性相关性的结构可靠性优化设计问题提供了有效工具。首先根据数据样本通过极大似然法和AIC准则选择出最优Copula；其次，由最优Copula函数和各变量的边缘分布构建出联合概率分布函数；最后，将联合概率分布函数用于可靠性分析，从而求解RBDO问题。两个数值算例验证了本文方法的有效性，结果表明：Copula函数的类型对优化结果有较大影响；在某些存在复杂相关性的情况下，使用传统的Nataf变换可能得到不可靠的优化结果；通过Copula函数，能够描述变量间的非线性相关和尾部相关性，从而提高优化结果的精度。此外，本文方法主要针对二维相关情形，未来可引入Vine-Copula等模型对本文方法进行拓展，从而求解变量间存在复杂多维相关性的RBDO问题。