关于蛇形摆运动原理与模式的探究
2018-10-20陈星辰
陈星辰
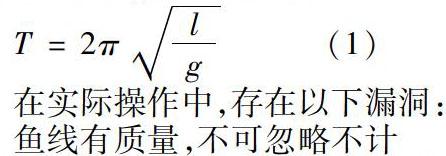

摘要:本次实验的内容为制作一个蛇形摆,通过制作过程可探究出蛇形摆的运动原理与运动模式,从而达到实验目的。
关键词:蛇形摆运动规律;简谐运动;摆长分析
中图分类号:G633
文献标识码:A
文章编号:1672 - 9129( 2018) 12 - 0204 - 01
1 实验设计与过程
单摆的摆动周期与摆长关系如下
T=2π√l/g (1)
又Ti+l= (i+l/i)*Ti (2)
易推出li+1=li(i+1/i)2 (3) 及 Ti+ l/i+1= Ti/i=a(a为正实数) (4)
则可得
li= ga/4π2*Ti2 (5)
由该表达式可知摆球下端落点在一抛物线上,且摆长长度为该抛物线上小球下端落点所在坐标的纵坐标的绝对值。但由于所给支架高度有限,故无法取理论分析表达式中的第一至连续i个点坐标作为摆球坐标。于是改变思路,取抛物线中间某段连续i个点,并以这些点作为摆球的坐标点设置摆长。
因每球摆长不同,故周期不同。为减少误差并便于实际操作,取每球周期的最小公倍数,并以此为根据计算出摆长。(因无法保证计算出的摆长为整数,故当计算结果为小数时取小数点后三位记录)实际操作时,考虑到支架高度,定周期为40s,取i=21,22,23…..32共12个值,计算摆长,计算结果均精确至小数点后三位。考虑到固定小球的鱼线问题,舍弃以单线系住小球的方案,而代以双线绕过小球上的环的方案。
当制作蛇形擺支架时,以晾衣架式结构为模型制作,即两边分别以两个木条交叉成A型,在木条上端交口处中间放置横梁,下可悬挂摆球。制作支撑用木条时将长方体木条两端削成梯形,并使底边与地面呈65°倾斜。待两边完成后将横梁放置于交口之上,以钉子钉牢。完成后整个装置重心不稳,易向左右两侧滑动。故另拿俩木条钉在支架中央,使三木条组成A型,以形成三角形稳定结构,如此可确保摆球摆动时支架不随之晃动。
按照所设计的实验方案,决定先制作支架和可悬挂摆球的横梁。支架完成后,曾考虑以胶水粘结横梁与支架,但因担心实验效果不理想,遂改变思路,改用钉子钉住横梁与支架。两者固定好后,再用短木连接两侧支架的站脚处,并同样以钉子固定,使短木与支架呈现A型。支架完成。
于横梁上每隔12厘米打两个空,用于悬挂小球的鱼线穿过。以卷尺量出横梁到摆球重心的距离来确定摆球悬挂高度和位置。鱼线缠绕住小球后,将鱼线从横梁上打孔传出,将小球拉至正确位置后绷紧鱼线,系紧打结固定鱼线,由此一个摆球便摆好。仿照第一个球的绑法,继续绑定另外11个摆球。当绑好前两个球时,我们进行了测试,发现两球摆动确实成周期性变化,但与预定周期相差较多。在确认计算结果,操作准确无误及摆长正确的情况下,推测是由于摆球摆动时自身旋转加快了摆动速度,从而加快了周期。于是在原有基础上,在每个摆球与鱼线交界处,另拿鱼线缠住,使摆球自旋频率下降。改进后继续进行测试,实验数据基本与计算结果吻合。因存在摩擦,气温,湿度等种种不可抗力因素,测定结果无法做到百分百吻合,但已尽可能减小误差,使结果尽量精确。后又用同样方法绑定其余10个摆球。
2 实验误差
制作出了蛇形摆,最初可见蛇形运动,后又改变为如两列不同摆动,又改变为如两列交错摆动。经约38s后,发现一个周期完成,摆球整体又重新回到初始状态,重新呈现为蛇形运动,周而复始。
遗憾的是,该周期与测定结果相差2s,且整体经38s后回到初始状态时,部分摆球并未继续如初始状态运动,导致蛇形运动不够明显。
3 对实验误差可能原因的分析
3.1 最有可能的误差便是简谐运动的局限性造成的。单摆是一种理想的物理模型,它由理想化的摆球和摆线组成.摆线由质量不计、不可伸缩的细线提供;摆球密度较大,而且球的半径比摆线的长度小得多,这样才可以将摆球看做质点,由摆线和摆球构成单摆.在满足偏角小于10°的条件下,单摆的周期方为
T=2√l/g (1)
在实际操作中,存在以下漏洞:
鱼线有质量,不可忽略不计
摆球的材质为铁,但其半径不满足比远小于摆线长度,因此不可看成质点,且其在运动中自身仍有运动,不存在可忽略不计的情况
3.2 在将球摆下时,由于人具有反应时间,因此在将贴紧摆球的挡板抽开时,计时无法做到与挡板抽开完全一致。
挡板自身有摩擦,在抽出时摆球自身便具有了一定加速度。(仅为猜测)
3.3 在摆球与鱼线交界处缠绕的鱼线使得其与摆球组成的整体的重心不再为摆球重心,摆长需重新测量,但我们并未重新调整便直接开始测量,导致实验出现了误差。
3.4 在计算过程中,重力加速度以10m/s2计算。但实验地的重力加速度并非10m/s2,需重新测量该地的重力加速度。
4 总结
蛇形摆是基于简谐运动的一种物理模型。在设计实验时,要考虑公式适用的条件,在可控范围内尽量满足公式条件,以确保实验之结果尽量精准。
