基于人工智能算法在医疗科技中的应用

孙嘉晨

摘要：在信息化時代随着大数据渗透到人类生产生活中的各个环节，医疗产业在人工智能技术中具有广泛应用和发展前景，研究人工智能技术在医疗科技中的应用具有重大现实意义。文章通过使用基本SQL结构化语句访问和处理数据库，配合数据库软件共同工作，使得处理医疗数据更加快捷。检索出数据后，建立不同分类模型，运用朴素贝叶斯、支持向量机和决策树三种算法完成分类任务，观察调整参数后对算法性能的影响，并通过分类器输出的结果比较三种算法预测的准确率、召回率和速度。最后总结分析出不同疾病最适合的算法。该算法兼顾数据处理的精确率与速度，结果可靠，可为医疗数据处理提供参考。

关键词：人工智能;SQL结构化语言;朴素贝叶斯算法;决策树;支持向量机;医疗科技

中图分类号：R - 05;TP18

文献标识码：A

文章编号：1672 - 9129（ 2018） 12 - 0107 - 03

1 引言

全球人工智能行业发展迅速的今天，人工智能技术的应用在各个行业逐渐兴起，带来了许多实际的商业价值，而在数据基础方面较为突出的医疗领域与人工智能的结合已然变为市场关注的焦点。由于医疗数据的海量性、多样性、诊断性、时间性、不规范性和隐私性等，处理医疗大数据的任务繁琐、难操作、不够精准，将人工智能技术引入医疗领域，可以将其应用在智能药物研发、智能诊疗和智能健康管理系统等方面，从而大大提升医生的诊疗效率和准确度、医药研发的速度等。本文主要在医疗数据的检索和分类上进行实验探究，首先根据医生的不同要求编写基本的SQL结构化语句，取回和更新数据库中的数据，检索出患者的电子病历和基本信息，针对数据结果形成图表，方便医生参考与统计。接着分别运用朴素贝叶斯算法、支持向量机和决策树三种常见的机器学习算法。其中朴素贝叶斯算法是基于贝叶斯定理和条件独立假设的分类方法，使后验概率最大化，期望风险最小化;支持向量机是从先行可分情况下的最有分类面发展而来，把低维线性不可分的数据通过核函数映射到了高维空间;决策树是运用分类的一种树结构，其中每个内部节点代表某个类或类的分布。三种算法各有特点，我们需要应用算法实验来证明不同数据集最适合的运算方法。

2 SQL实验

SQL指结构化查询语言，即访问和处理数据库的计算机语言，使我们有能力访问关系数据库。SQL语句主要用于取回和更新数据库中的数据，配合数据库软件共同工作。

SQL语句的四种基本类型有增（INSERT）、删（DELET）、改（UP-DATE）和查（SELECT）。本次试验中，我们运用到了以下几种基本语句：“Select * from”用来检索所有行和列，“Order hy”语句的作用是排序检索数据，而“Where”语句用于过滤数据。主要运用到三种函数：“COUNT函数”返回匹配指定条件的行数，“SUM函数”返回数值列的总数，“AVC函数”返回数值列的平均值。

2.1 医疗统计分析基础

（1）统计卒中筛查数据表中总共包含多少档案：

SELECT acid，COUNT （acid）| FROM archivescases

筛查结果为：acid=3887781，COUNT（acid）=10000。

（2）统计卒中筛查数据表中男性数量

SELECCT asex， COUNT （acid） FROM archivescases

aSex='男'

筛查结果为：aSex=男，COUNT（ acid） =4996。

（3）统计卒中筛查数据表中女性数量

aSex， CcUNT（acid）

archivescases

aSex='女'

筛查结果为：aSex=女，COUNT（ acid） =5004。

（4）分别统计卒中筛查数据表中年龄在“20 - 60”，“60以上和20以下”的人数

SELECT COUNT （acid）

archiverceses

acAge=20 AND acAge<=60|

SELECT COUNT（acid）

archivescases

acAge<20 OR| acAge>60

统计结果分别为：COUNT（acid） =5790;COUNT（ acid） =4210。

2.2 医疗统计分析提高

（1）使用一条语句统计卒中筛查数据表中各有多少男性和女性，并画出图形比较，如图1所示。

SELECT aSex，COUNT （acid） FROM archivescases

aSex|

（2）使用一条语句统计卒中筛查数据表中受教育程度的人数分布，并画出图形比较

SELECT acEdu， COUNT （acid）

archivescases GROUP BY acEdu|

统计结果为：acEdu=“小学，初中，高中，本科，硕士，未填”，相对应COUNT（acid）分别为“4837，2485，923，347，3，1405”，饼形统计图如图2所示。

（3）统计男性中吸烟人数

1 SELECT

2 dangerfactors.dfSmoking，

3 COUNT （dangerfactors，acid）

4 FROM

5 archivescases，

6 dangerfactors

7WHERE

8 archivescases. acid = dangerfactors. acid

9 AND archivescases.aSex ='男'

10 AND dangerfactors.dfSmoking='1'| 统计结果为：男性中吸烟人数为：1024。

（4）统计女性中高血压人数

1 SELECT

2 dangerfactors.dfHypertension，

3 COUNT （dangerfactors.acid）

4 FROM

5 archivescases，

6 dangerfactors

7 WHERE

8 archivescases.acid = dangerfactors. acid

9 AND archivescases.aSex ='女'

10 AND dangerfactors.dfHypertension='1'|

统计结果为：女性中高血压人数为：1153。

2.3 医疗统计分析实际应用

统计既往脑卒中在各个年龄段的分布（按照10岁作为一个年龄段）

1 SELECT B.dfStroke，sum（CASE WHEN CAST（A，acAge AS DECIMAL） BETWEEN 0 AND 39 THEN 1 ELSE 0 END） AS '[0-39l'，

2 sum（CASE WHEN CAST（A，acAge AS DECIMAL） BETWEEN 40 AND 49 THEN 1 ELSE 0 END）AS '[40.49l'，

3 sum（CASE WHEN CAST（A，acAge AS DECIMAL） BETWEEN 50 AND 59 THEN 1 ELSE 0 END ） AS '[50-59]'，

4 sum（CASE WHEN CAST（A，acAge AS DECIMAL） BETWEEN 60 AND 69 THEN 1 ELSE 0 END ） AS '[60-69]'，

5 sum（CASE WHEN CAST（A，acAge AS DECIMAL） BETWEEN 70 AND 79 THEN 1 ELSE 0 END ） AS '[70-79]'，

6 sum（CASE WHEN CAST（A，acAge AS DECIMAL） >80 THEN 1 ELSE 0 END ） AS '[>80]' FROM dangerfactors B join archivescases A on B，acid=A，acid where B，dfStroke='l' ; 统计结果为：[0 -39] =0;[40 -49] =18;[50 -59]=56;[60 -69]=135;[70-79] =64;[>80] =14.

3 人工智能算法

3.1 朴素贝叶斯算法。贝叶斯算法是基于贝叶斯定理和条件独立假设的分类方法，通过联合概率建模，运用贝叶斯定理求解后验概率，将后验概率最大者对应的类别作为预测类别，因为后验概率最大化，使期望风险最小化。

朴素贝叶斯算法相关公式为：

P（Y∣X）=PP（X，Y）/P（X）=P（X∣Y）P（Y）/∑YP（X∣Y）P（Y） P（X=x∣Y=ck）=n∏j=1 P（Xj=xj∣Y=Ck）j=1，2，…K

式中，j表示數据特征向量的维数，Ck表示第k个类别。朴素贝叶斯算法由训练集样本数据计算得到先验概率分布P（Y= Ck）和条件概率分布P（X= XI Y=Ck），从而计算可得联合概率分布P（X，Y）[1]。

3.2 决策树。决策树是运用分类的一种树结构，其中每个内部节点代表某个类或类的分布，贪心算法是决策树的基本算法，算法计算的基本步骤为[2-3]：

（1）创建代表数据集的单个节点N。

（2）如果所有样本都属于同一个分类C，则该节点为叶节点，并以分类C进行标记。

（3）否则，选择属性列表中最有分类能力的属性作为测试属性。

（4）对所选属性的每个已知值，创建一个分支，并按此将样本集合划分为若干个数据集。

（5）算法采用相同的过程，递归生成各数据集上的样本决策树。

（6）递归划分过程当下列条件之一成立时停止：①给定节点的所有样本属于同一分类;②属性列表中所有属性处理完，没有剩余属性可用来进一步划分样本;③节点上的数据集为空。

3.3 支持向量机。支持向量机是从现行可分情况下的最有分类面发展而来，把低维线性不可分的数据通过核函数映射到了高维空间，研究的问题主要是求解凸二次规划[4]，其基本原理是建立在vc维理论与结构风险最小原理基础之上，根据有限样本在模型复杂性和学习能力间寻求最优折中值，从而获得最佳推广能力[5 -6]。

支持向量机是根据已有训练集

T={（x1，yl），（x2，y2），…（xl，yl），∈（X，Y）l}

寻找实数空间上的一个实值函数g（z），以此用函数f（ xsgn（g（x））推断任一模式x对应y值的问题。

4 基于人工智能算法的医疗科技应用

4.1 实验步骤。

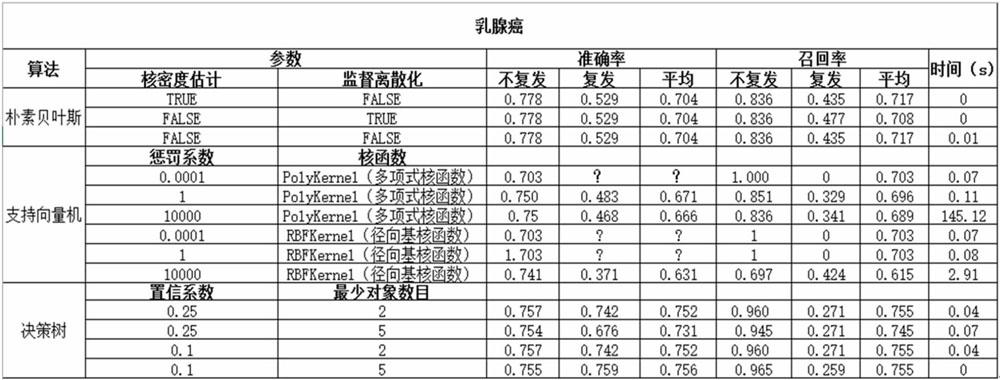
（1）在乳腺癌数据集上完成分类任务，建立不同分类模型，通过调整三种算法的参数对数据对象进行分析，并对分类器的输出结果进行比较和分析。

（2）记录调整的参数与输出结果，制成表格。

（3）预测的准确率与召回率比较。

准确率=检索列的相关文件/所有检索到的文件总数

召回率=检索到的文件总数/所有相关的文件总数

（4）分类速度比较。

（5）分析与讨论，得出最适合此疾病的算法。

4.2 人工智能算法在乳腺癌中的应用。实验发现，朴素贝叶斯算法中，监督离散化调为“false”时，准确率和召回率较高，时间较短，为朴素贝叶斯算法中最适合的调参方法;而在支持向量机算法中，惩罚系数为1时准确率和召回率较高，时间较短，我们还发现将惩罚系数改为10000时，计算运用时间较长，而惩罚系数调为0.0001时，会出现无法运算出结果的现象;在决策树算法中，小幅度调整参数对结果并无过大影响，时间都较短，准确率、召回率较高。乳腺癌在朴素贝叶斯、支持向量机和决策树三种算法中的结果对比如表1所示。

4.3 人工智能算法在心脏病中的应用。在朴素贝叶斯算法中，只将监督化离散调整为false时间较短，其余参数调整对实验结果影响不大，时间也都较短;在支持向量机算法中，将惩罚参数调大实验时间会过长，不适用于某些有时间需求的医疗方面;在决策树算法中，置信系数为0.1，最少对象数目5时最为合适。心脏病在朴素贝叶斯、支持向量机和决策树三种算法中的结果对比如表2所示。

4.4 结果分析。根据前面详细分析与论述，由表1和表2可知：对于乳腺癌，最适计算方法为决策树，调整参数为“置信系数0.1，最少对象数目5”。對于心脏病数据集，最适运算方法为支持向量机，调参为“惩罚系数1，多项式函数”。

参考文献：

[1]邹晓辉.朴素贝叶斯算法在文本分类中的应用[J].数字技术与应用，2017（ 12）：132 - 133.

[2]王知津，周鹏，韩正彪.基于决策树算法的竞争对手识别模型研究[J].情报理论与实践，2016，36（3）：1-5.

[3]王保义.客户关系管理中客户细分的数据挖掘[D].西安：西安电子科技大学，2009.

[4]汪海燕，黎建辉，杨风雷.支持向量机理论及算法研究综述[J].计算机应用研究，2014，31（5）：1281 -1286.

[5]张松兰.支持向量机的算法及应用综述[J].江苏理工学院学报，2016，22 （2）：14 - 21.

[6]黄文，王正林.数据挖掘：R语言实战[M].北京：电子工业出版社.2014.