面向多任务的工业机器人运动轨迹优化研究

江西制造职业技术学院 机电工程系 郝 勇

随着工业化生产规模的扩大，工业机器人逐渐代替人力开始投入生产，不仅增加了产品生产量，产品质量也有了很大的提高。但是在实际应用过程中，工业机器人有时会出现抖动以及机器人末端执行器不能完全按照规定运动到准确位置等问题，在一定程度上影响了工业生产。针对这一情况，提出了一种面向多任务的工业机器人运动轨迹优化方法，以期改善工业机器人操作质量。

0 引言

改革开放后，工业生产规模逐渐扩大，为我国经济的发展的提供了有力的支持。工业机器人的投入使用有利于提高工业生产质量、改善劳动条件、提高生产效率、节省劳动成本等。然而在实际生产过程中，工业机器人在启动、运行或者停止运行的时候出现手部抖动、以及机器人末端执行器不能完全按照规定运动到准确位置等以及其它问题[1]。这些问题的出现严重影响了生产质量，加快了机械部件的磨损，提高的维修成本。为解决这一问题，使机器人能够在高速、平稳的状态下抵达所预定的位置，就需要在操作机器人工作之前对其进行运动轨迹规划并优化，从而避免上述不良现象的出现。本次研究针对多个轨迹跟踪任务，提出一种面向多任务的工业机器人运动轨迹优化方法，为解决上述问题进行深入探讨。

1 工业机器人运动轨迹规划

机器人是自动执行工作的机器装置，主要由机械身体、记忆或程序功能和核心零件等组成[2]。而应用在工业生产中的机器人不是传统意义上的模拟人型外表的机器人，而是一种拥有机器人功能性质的机器臂或机械手。工业机器人能够模拟人力进行自动化操作，以便完成各种生产作业。下图1为一个工业机器人操作流程。

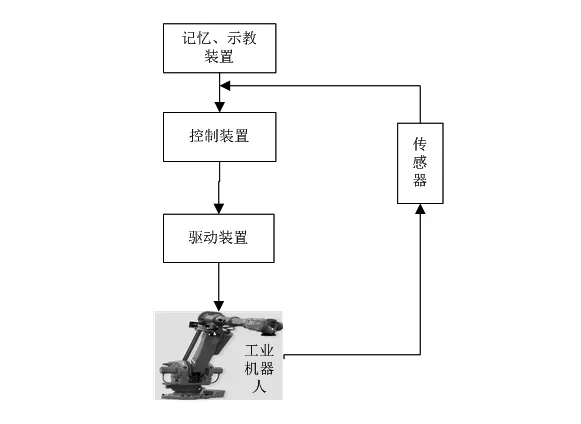
图1 工业机器人操作流程

首先需要将工业机器臂或机械手固定在一个具体位置或安置在重复运动的机械小车上，然后按照人为设置好的程序规则进行重复活动，如刨、捏、拽、牵、撕、打、剪、磨、握、抓等。工业机器人最大的优点是能够不厌其烦的一直进行重复性操作；适应性强，无论是在多么恶劣的环境中，都可以毫无阻碍的完成工作。

轨迹问题可以通过以下三个方面描述出来：机器臂或机械手的位移、速度和加速度。工业机器人运动轨迹问题就是在具体作业任务的要求下，通过计算来预测出其工业机器人的运动位移、速度和加速度的变化规律。而运动轨迹优化就是利用一种优化算法找出一条能够满足各种性能指标和边界约束条件的运动轨迹。

1.1 坐标系空间构建

本次运动轨迹优化研究选用ABB公司生产的型号为IU*099的工业机器人，它是一种最常用的六自由度工业机器人。

现通过拉格朗日方程求得其动力学公式：

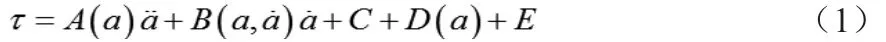
公式中，A为运动惯性矩阵；a为关节变量； B为离心力与科式力相关系数矩阵；C为关节摩擦；D为重力矩；E为干扰因素矩阵。

由上面的公式（1）可以得到关节空间速度与工作空间各个坐标变量之间的速度映射关系：

公式中，X为坐标变量向量。

1.2 空间转换

要实现直角坐标系空间到关节空间的转换，就要解决逆运动学的求解问题。现通过上述公式（2）来反求出IU*099机械手臂的各个关节角度。若机器人位姿A是若干关节变量a的函数，则机器人手部位姿的变化dAn是由各个关节的微小运动dai决定的。

公式中，J为机器人末端坐标系的雅克比矩矩阵。

具体求解算法步骤需要在Matlab软件中计算完成。

url: ‘/xpage/form/getform?id=tob_home_left’;

success: function (data) {读取初始的迭代角度

if (data.status.code === 0) {

var model = data.data.form_data && data.data.form_data.model; 用正

运动学得到迭代过程中末端位姿矩阵

if (model && model.length ＞ 0) {

render(model);

计算位姿与位姿气的差

＜%var docList = data[i][‘related_doc_infos’];%

＜div class=”＜%=status%＞”＞

＜div alog-group="view.strurecom.doc"＞到相对机器人相对于基

坐标系雅克比矩阵

＜div class=”guess-u-like”＞

%for (var j = 0, n = docList.length; j ＜ n; j++) 各个关节变量的微小变化

＜%// mark_pay_doc：＜div class="image-wrap"＞

＜a href=”/view/＜%=docList[j][‘doc_id’]%＞.html”

更新当前值

data-mark-pay-doc=”＜%=markPayDoc%＞”

target="_blank" class="logSend log-xsend fcClick" 是否满足更迭条件

data-logsend="{'send':['view','doc_link',{'from':'srs','tag_no'

＜% _.each( commentList, function( item ) { %＞＞

＜li class="ct-item" data-reply-id="＞＜%= 返回步骤三item.reply_id %＞"

id="item-＜%= item.reply_id %＞"＞

＜div class=”ct-item-wrap”＞

＜div class=”clear fi x

ct-con-wrap"＞结束更迭

＜div class=”ct-extra-into”＞

＜p＞＜%= item.create_time %＞＜/p＞

＜p＞

2 运动轨迹优化算法

在工业生产中，人们总是想要在最短的时间内尽可能完成更多的工作。所以本次优化研究就以关节速度、加速度作为约束条件，来完成对工业机器人运动轨迹的优化。

2.1 确立约束条件

首先设立目标函数：

然后确定变量：

最后确定约束条件：

（1）速度约束条件

式中，θt为t时刻内最大关节速度；为工业机器人某个关节允许的最大关节速度。

（2）加速度约束条件

式中，αt为t时刻内最大关节加速度；βmax为工业机器人某个关节允许的最大关节加速度。

综上所述，得到基于时间最优的机器人轨迹优化问题，表示为：

2.2 遗传算法求取最优解

遗传算法是以达尔文的进化理论作为基础，通过多次遗传更迭来逐渐得到最优解。

将上述确立的约束条件作为遗传算法的惩罚函数：

2.2.1 染色体编码

运动轨迹优化目的是为寻找在约束条件内，最短的时间间隔，要对工业机器人每完成一次的运动的时间间隔进行编码，采取的编码方式为:和其中的5段时间间隔相对应，编码设定为长度为5的定长方式，采用实数编码。编码每一位为-1到1之间的随机数。

2.2.2 遗传算子

将选择算子和交叉算子选为遗传算法工具箱的默认设置，而变异算子则采用非一致变异方式。

于是，通过遗传算法可以求解出适应度函数在最小时机器人各段轨迹的最优时间间隔，完成运动轨迹优化。

3 结束语

工业机器人应运而生，在工业生产中发挥了巨大作用，但是在实际生产过程中，工业机器会出现抖动、运动轨迹偏差问题，使得机械化生产质量受到严重影响。针对这一情况，本次研究提出一种面向多任务的工业机器人运动轨迹优化方法。通过对轨迹的优化实现工业机器人的平稳运作，精确生产。这对于工业生产向着机械化、自动的方向发展具有重要的指导意义。