转子导程及偏心率对面团混合器混合流场及效率影响分析

朱向哲，高 鹤，刘 俭



转子导程及偏心率对面团混合器混合流场及效率影响分析

朱向哲，高 鹤，刘 俭

（辽宁石油化工大学机械工程学院，抚顺 113001）

为了探究偏心螺旋转子扰动下面团混合器的混沌混合机制，明确偏心转子系统的关键几何参数对混沌混合机制的影响，从三维Lagrangian的新视角，利用有限时间Lyapunov指数（finite-time lyapunov exponent, FTLE）和拉格朗日拟序结构（lagrangian coherent structure, LCS），结合经典Poincaré截面，对面团混合器的流体输运和混合机理进行了深入研究。利用LCS的准边界特性，分析了混合器的混沌和非混沌区域分布规律；研究了转子偏心率对混沌尺度和非混沌区粒子运动特性的影响规律。利用剪切速率、对数拉伸、瞬时混合效率和平均时间混合效率等，分析了转子导程和偏心率对混合器混合效率的影响。结果表明，双曲LCS将混合器流域划分为两个不同动力学特性的区域：内回转区和外螺旋区。随着转子偏心率逐渐增大，外螺旋区流体的混沌混合强度增大，内回转区混合强度逐渐较低，当偏心率较小时，流体混合以内回转区运动为主；由于转子扰动减小，减小了混合器的轴向物质输运。从拉伸流动混合效率角度可知，当导程=120 mm、偏心率=0.67时，混合器的具有相对较高的拉伸混合效率；当导程=60 mm、偏心率=0.33时，混合器的拉伸混合效率相对最低，但其剪切混合效率相对最高。该文为食品及其它混合设备的设计和优化提供了新的研究思路和理论依据。

混合器；食品加工；流场；偏心螺旋转子；有限时间Lyapunov指数；拉格朗日拟序结构；Poincaré截面

0 引 言

混合是食品连续加工过程中的重要环节，其均匀性是影响产品品质的主要因素之一。近年来，随着对高品质食品需求的日益增加，提高了对食品混合、特别是面团混合质量的要求[1-2]。面团等食品具有复杂的流变性和高黏度特性，面团中的脂质、蛋白质、面筋等含量对于其流变性以及对产品品质的具有一定的影响[3-4]；同时，面团中气泡的数量和气泡尺寸影响面团的氧化过程[5]，最终影响到产品的品质，并且面团混合过程的时间也不宜太长。因此，要想获得预期的混合质量，对食品的混合加工设备也提出了更高的设计要求。

高效食品混合器设计和优化的核心是对混合设备中的面团等食品流体混合机制的深入理解。Connelly等[6-7]采用数值模拟，利用速度场剪切应力、混合指数和分离指数等参数表征了单螺杆和双螺杆挤出机二维流场面团流体的混合机制，研究表明，二维螺杆流场内物料主要的混合方式为线性剪切、流动拉伸，分布混合以及分散混合。林江娇等[8]建立了双螺杆挤压膨化机中玉米物料的非等温、非牛顿流体的模型，分析了双螺杆挤压膨化机内流体的温度变化过程及规律，并进行了试验验证。孙智慧等[9]采用ANSYS软件对食品双螺杆挤出机中流体的速度场、压力场进行了仿真研究。通过后处理，得到了多种工况下的比能耗，并对仿真结果进行了试验修正。朱向哲等[10]采用三维流-热耦合模型对三螺杆挤压机流场、温度场、压力场和粘性生热分布进行了研究；分析了螺杆转速、螺纹头数、压力差和挤出量等参数对三螺杆挤压机挤出功耗和比能产量的影响。Chella等[11]分析了面团流体在偏心转子周期性运动规律，研究发现面团流体在偏心转子的周期性扰动下，虽然不能依赖湍流扰动使流体混合的均匀，但产生混沌混合机制。Chien等[12]又对有周期性边界变化的空腔流动进行了试验和数值模拟，发现了混沌特性依赖于边界的周期变化规律，并伴有分岔现象。混沌对流显著提高了流体层流的混合效率，成为强化高粘度流体混合的重要的手段。

最近，Hosseinalipour等[13-14]利用混沌混合理论，研发了具有螺旋式偏心转子的面团混沌混合器；利用粒子追踪、Lyapunov指数、混合指数等对混沌混合器的混合机理进行了理论和实验研究。研究表明，该混合器利用混沌对流显著提高了设备的混合效率；同时，也克服了螺杆挤压机等传统混合设备的高剪切应力对长分子链流体的剪切破坏。然而，上述采用传统的欧拉方法研究混沌流场不能有效识别流场的物质输运边界，难以刻画出混合系统的潜在几何学和动力学特性[15-17]；对于深刻理解混合设备的流动和混合机理具有一定的局限性。

近年来，在传统欧拉体系流动分析的基础上，提出了拉格朗日拟序结构（Lagrangian coherent structure, LCS）分析方法。基于有限时间李雅普诺夫指数（Finite-time Lyapunov exponent, FTLE），得到了系统的LCS，为研究不稳定流体的运输行为提供了有利工具[18-20]。目前，FTLE和LCS作为分析流体动力学行为的主要方法，广泛应用于大气、海洋流动、湍流和微流体混合等不同领域[21-26]，但该方法应用于食品加工设备的研究还十分有限，未见相关研究报道。本文从三维拉格朗日全新思路出发，利用FTLE和LCS，结合经典Poincaré截面，对螺旋式偏心转子食品混沌混合器的流体输运和混合机理进行了深入研究。利用LCS的准边界特性，分析了面团混合器的混沌和非混沌区域分布规律；研究了转子的偏心率对混沌尺度以及非混沌区流体动力学特性的影响，给出了混沌尺度对于混沌混合器的对数拉伸、混合效率和混合时间的影响规律；为食品加工设备的设计、优化和研发提供了新的理论依据，也为其它混合设备的设计提供了新思路。

1 数学模型

本文对混沌混合器内加工小麦面团流体的流动过程进行数值模拟，采用如下基本假设：1）混合为等温过程，流场各点温度一致；2）流体充满整个流域且流体不可压缩；3）小麦面团流体为高粘度流体，流动为层流，忽略惯性力的影响；4）边界无滑移；5）体积力忽略不计。

混沌混合器内小麦面团流体运动的连续性方程、动量方程和本构方程分别为[6]

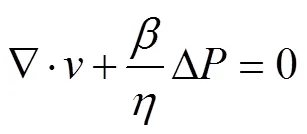
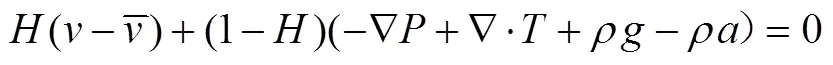
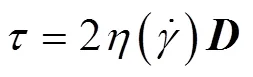
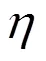
小麦面团流体具有非线性和粘弹性等，可以采用Bird-Carreau模型描述小麦面团的复杂流变行为[27-28]，其本构模型为

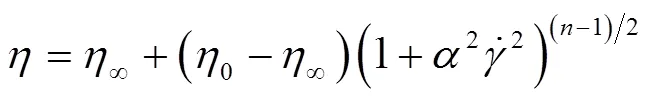
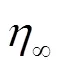
2 计算方法

2.1 FTLE和LCS

Poincaré截面和Lyapunov指数分析流场动力学特性的重要工具，它们可描述动力系统的长期行为。然而，在实际工程或实验室研究中，长时间追踪粒子轨迹难以实现，尤其是在运动范围有限的情况下，需要一种对动力系统短时间状态的刻画参数。FTLE是一种能够有效刻画动力系统短时间状态的参数[19]。基于流场内流体单元产生的最大拉伸率来代表各个位置的变形状态，从而得到流场的FTLE数值，其计算公式为[20]

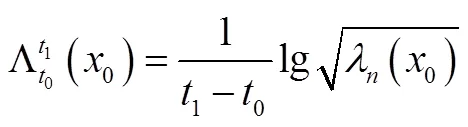
将FTLE与流场坐标结合，获得空间中的一个代表拉伸强弱的曲面。若存在某一范围内的突出点，则为流场内局部最大拉伸位置，若这些点连成峰，构成FTLE中的脊，即LCS。由正向时间积分所得的LCS表明流体的分离特征，称为排斥的LCS；相反，由负向时间积分所得的LCS表明流体的聚集特征，称为吸引的LCS。由于LCS稳定性较强，在较大的速度场误差下仍可保持其稳定性，可获得相对准确的LCS[20]，这为流场中混沌结构的识别提供了一种较为可靠的研究方法。

2.2 LCS计算方法

由于混合器的几何结构具有周期性，因此采用分步式计算混合器流场的LCS分布，即通过对速度场的向前时间积分获得排斥的LCS，对速度场的向后时间积分获得吸引的LCS，积分时间选取转子旋转周期的整数倍（本文所提及的1个周期为转子旋转一周的时间），以保证排斥和吸引的LCS处于同一动力系统中。

对于LCS的计算一般基于有限时间内最大拉伸率FTLE的结果。假设混合器内流体的三维速度场可描述为

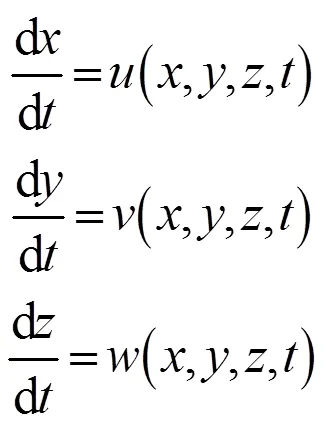
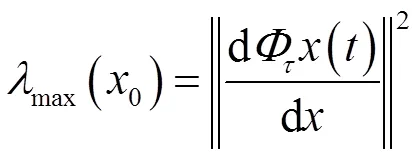
3 物理模型

面团混沌混合器几何模型如图1所示。其中，螺旋式偏心转子是混沌混合器的核心部件，转子绕中轴线匀速转动。在混合器的不同轴截面，由于偏心量的存在引起流体脱离流线，引发了流场的混沌特征。转子及机筒的主要几何参数如下：螺旋转子截面圆半径r= 25 mm，流域半径r=40 mm，导程=120 mm，为偏心距。为了定性描述转子几何结构，引入无量纲参数：间隙率和偏心率分别为

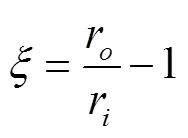
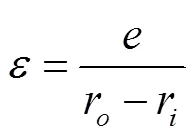
根据混合器试验样机具体设计工况，选取间隙率=0.6，偏心率分别选取为0.97、0.67、0.33。对比研究不同转子偏心率对混合器流体输运和混合动力学特征的影响。

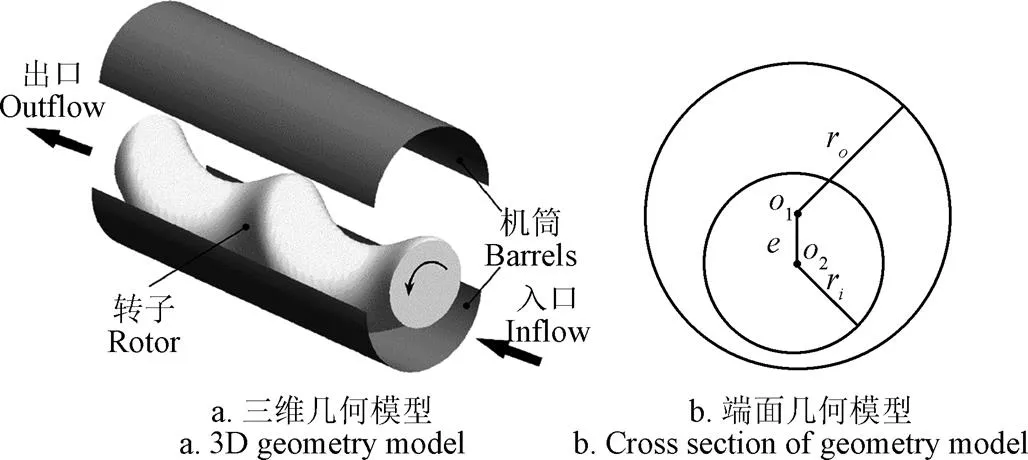
注：ri螺旋转子截面圆半径，mm，ro为流域半径，mm，ε为偏心距，mm，O1，O2为圆心。

采用Gambit软件进行几何建模，利用Polyflow软件的网格叠加技术（MST）进行网格划分[29]，混合器转子和流域均采用六面体单元进行网格划分。为捕捉流场中转子与筒壁间隙中流体的运动，转子和筒壁采用4 层边界层网格。为了缩短计算时间，转子采用空心结构，以便减少网格和节点的数量。混合器流域与转子的网格划分方法如图2所示。其中，转子的网格数为1 115 856个，流域（流道）的网格数为561 392个。采用Polyflow软件求解控制方程，收敛精度为1×10-4。

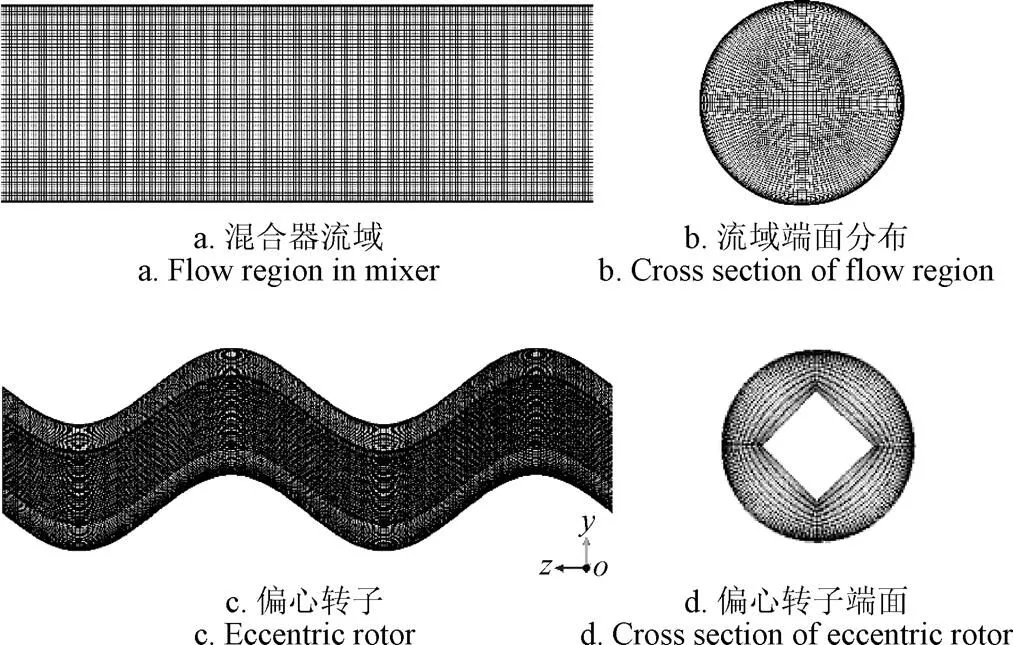
图2 混合器流域与转子的网格划分

4 结果与讨论

4.1 试验验证

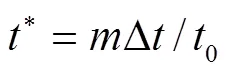
注：每幅图左侧为试验结果，右侧为数值模拟结果

注：每幅图从左到右依次为t=T，t=2T，t=3T。

需要说明的是，数值模拟粒子轨迹的长度大于试验样本面团的扩散长度，这主要是因为实验面团示踪剂可视化截面的截取方法略有不同：文献[14]采用在混合器出口安装了一段30 cm长的实验圆管，通过截取不同时刻圆管端面的挤出样本，获取实验流体随时间变化的混合形态。而本文数值模拟粒子可视化追踪，直接把不同时刻流体粒子映射到流道出口截面，获得粒子可视化结果。

4.2 积分时间的选取

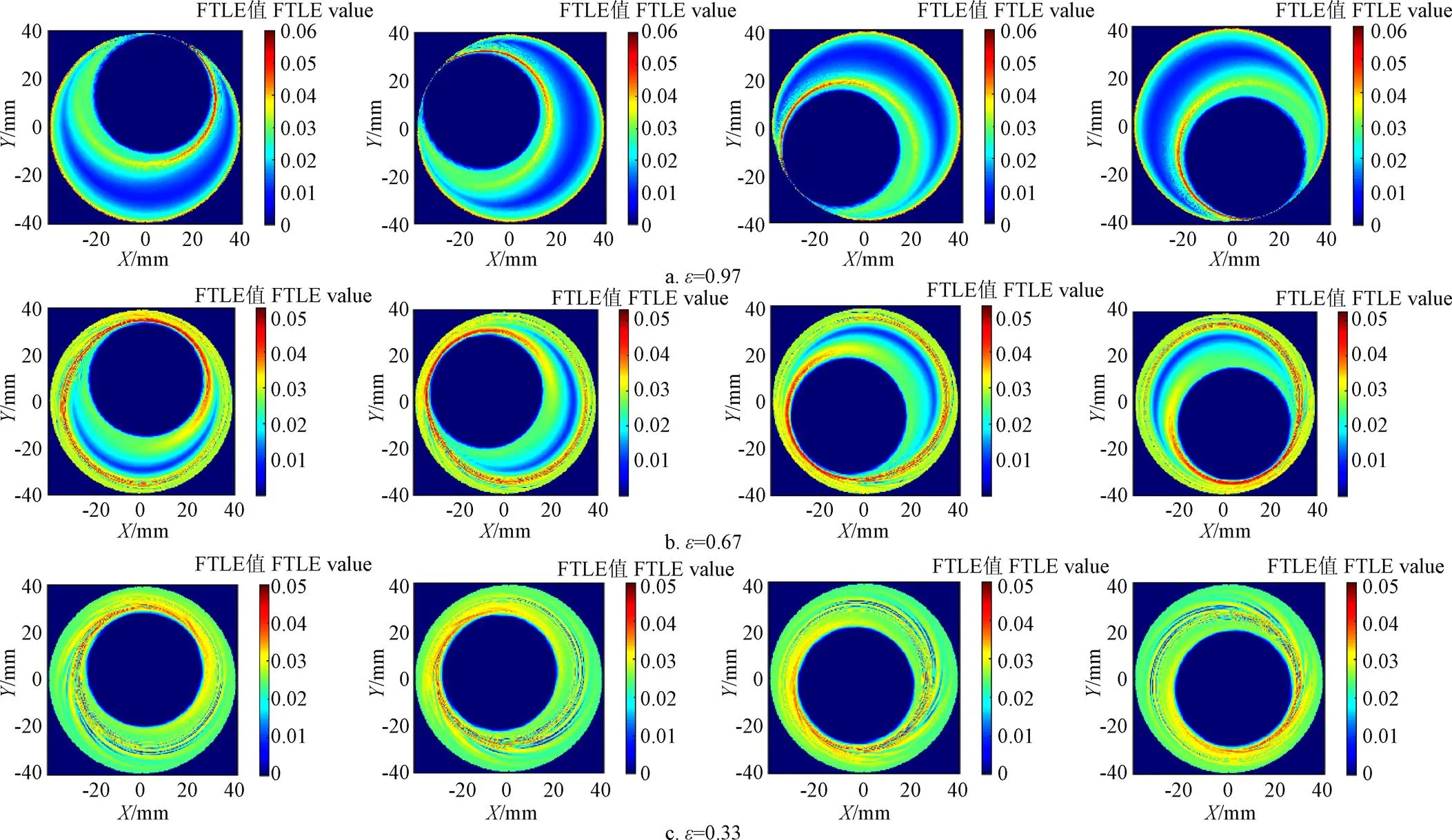
FTLE表示积分时间内流体的分离程度，积分时间影响LCS结构的清晰程度。积分时间过短，LCS结构不清晰；积分时间过长，LCS结构混乱难以识别。本文分别计算了3组不同偏心率转子混合器在积分时间分别为、2和3时间向前的FTLE分布，如图4所示。从图4中可以看到，随着积分时间的增加，具有较大FTLE值的红色“脊线”逐渐增加。当积分时间为2时，“脊线”结构趋于完整。当积分时间为3时，已难以分辨出3组模型“脊线”的主次。通过对三组模型不同积分时间向前的FTLE对比，本文选取2作为混合系统的积分时间。

4.3 LCS分布规律

LCS作为FTLE中的“脊”，代表了沿积分时间流场中分离程度较强的区域。在实际流动中，排斥的LCS代表拉伸效率较高的区域，而吸引的LCS则刻画了粒子的流动趋势。由于LCS具有物质的连续性，两侧的粒子在LCS上的交换微小，使得LCS成为流场中潜在的边界，即准边界[15]。选取转子螺旋导程长度的20%、40%、60%、80%所在轴截面，即分别为24、48、72和96 mm，其中转子沿方向每移动20%导程长度，转子端面逆时针转动72°。通过分析混合器不同轴截面的FTLE和LCS分布，研究混沌流场的几何学和动力学特性。

图5所示为积分时间为2时，混合器不同轴截面的时间向前FTLE分布。从图5可以看到，随着转子偏心率的减小，流域中流体受到拉伸的区域逐渐增大。在=0.97时，排斥的LCS紧贴在转子壁面以及混合筒内壁面，流域中心由于缺少LCS而整体呈弱拉伸状态。随着的减小，筒壁面排斥的LCS逐渐脱离壁面，向流域中心靠近，在=0.67时，排斥的LCS与筒壁产生一定的距离，一定程度上增加了中心区域流体的拉伸程度，弱化了对筒壁附近流体的影响，但在转子前进方向一端，排斥的LCS依然贴近转子壁面。当=0.33时，排斥的LCS占据流域中心，整体呈强拉伸状态；流域的弱拉伸区夹在排斥的LCS之间，此时靠近转子壁面排斥的LCS被弱化。

注：每幅图从左到右依次为Z=24 mm、Z=48 mm、Z=72 mm、Z=96 mm。

图6所示为积分时间为2时，混合器轴向2D剖面的时间向后FTLE分布。时间向后FTLE场中的“脊”为吸引的LCS，暗示粒子潜在的运动趋势。由图6可以看到，吸引的LCS将混合器内流域划分为两个具有不同粒子运动特性的区域，即：在吸引的LCS与筒壁之间的区域，粒子绕整个流域旋转，称为外螺旋区；在吸引的LCS与转子壁面所夹区域，粒子沿转子壁面旋转，形成内回旋区。由于LCS的准边界作用，外螺旋区和内回旋区之间很难进行物质交换。

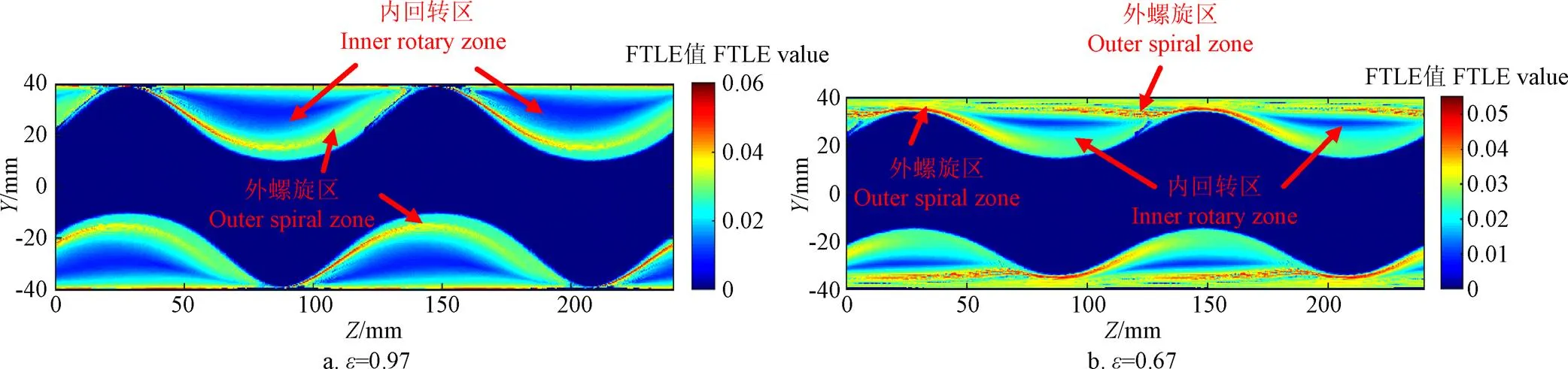
图6 混合器轴向2D剖面的时间向后FTLE分布

在一定条件下，排斥的LCS对应稳定流形，吸引的LCS对应不稳定流形；稳定流形和不稳定流形的交点，即双曲不动点与同宿或异宿点。为清晰地揭示流域的流形结构，将排斥与吸引的LCS合并于同一图中，并标识出LCS方向，以便确定流域中的流形结构。图7所示为排斥与吸引的LCS的合并图。从图7a可以看出，在偏心率为0.97时，筒壁处排斥与吸引的LCS重合，且具有相同的流动方向，均为顺时针。而靠近转子壁面的LCS则具有逆时针流向，LCS在转子与壁面的狭缝中方向发生改变，说明在狭缝中的LCS交点是双曲平衡点，此时，经过平衡点的排斥和吸引的LCS称为双曲LCS，而其余交点为同宿点；双曲点与同宿点为流场系统带来了混沌效应。但LCS分布较为集中，产生的混沌区域仅为转子壁面附近与筒壁附近的区域，中心流域则在LCS的影响下做月牙形运动。

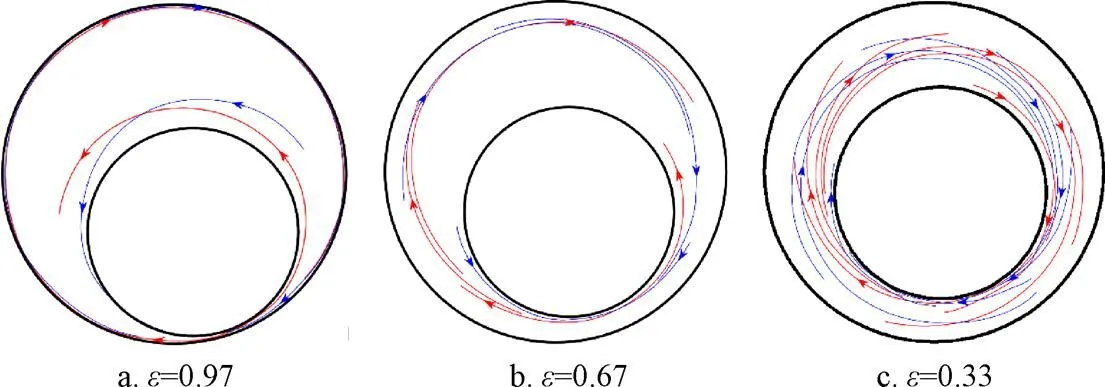
注：红色为吸引的LCS，蓝色为排斥的LCS；箭头代表流向。

当偏心率减小到0.67时，如图7b所示，LCS向流域中心缩小，同时排斥与吸引的LCS之间的交点增加，LCS流向与偏心率为0.97时相同，即环绕整个流域的LCS为顺时针流向，贴近转子壁面的LCS为逆时针流向，说明在转子与筒壁较小间隙处依然存在双曲平衡点。在LCS分布的区域，受到双曲点的影响，形成了混沌区。而流域中心缺少LCS的区域则在LCS的影响下做有规律的运动。随着偏心率的继续减小，当=0.33时，如图7c所示，排斥与吸引的LCS整体位于流域中心，但此时LCS的流动方向均为顺时针，无方向改变，因此整个流域在LCS的影响下绕中心轴进行螺旋运动，流场系统中虽有LCS，但不存在双曲LCS，导致流域内的月牙运动区域消失，同时由双曲平衡点引发的流体折叠作用也随之消失，降低了混沌混合效率。为进一步研究流域内没有LCS区域的运动形式和混合机制，将采用Poincaré截面对此部分进行分析。

4.4 Poincaré 截面分析

为了计算混合器内的Poincaré截面，取Z=96mm处的轴截面作为释放初始追踪粒子的平面，均匀覆盖整个截面。通过4阶Rung-Kutta积分法，选取适合的时间步长计算粒子的运动轨迹。记录粒子长期运动过程[12]。图8所示为追踪496个流体质点时，记录200个周期时不同转子偏心率的混合器Poincaré截面。从图8中可以看到，当偏心率=0.97时，筒壁与转子壁面粒子分布较为杂乱，形成混沌特征。而流域其他位置的粒子具有清晰的月牙状结构，与LCS所包围的区域相同。当偏心率减小到0.67时，月牙状结构缩小，并且在流域中出现明显的边界；此时混沌区的分布发生了显著改变，主要分布在靠近筒壁的环形区域内，在紧贴筒壁的流域内则为环形运动，且不与混沌区内的流体发生混合，在混沌区与转子壁面之间的区域内，流体粒子呈环形运动，被混沌区隔离。当偏心率进一步减小为0.33时，月牙形区域消失，流域整体呈弥散状，流体粒子整体沿筒壁的呈环形结构运动，虽然不同区域内的粒子做无规则运动，但不同区域之间的粒子交换甚少。

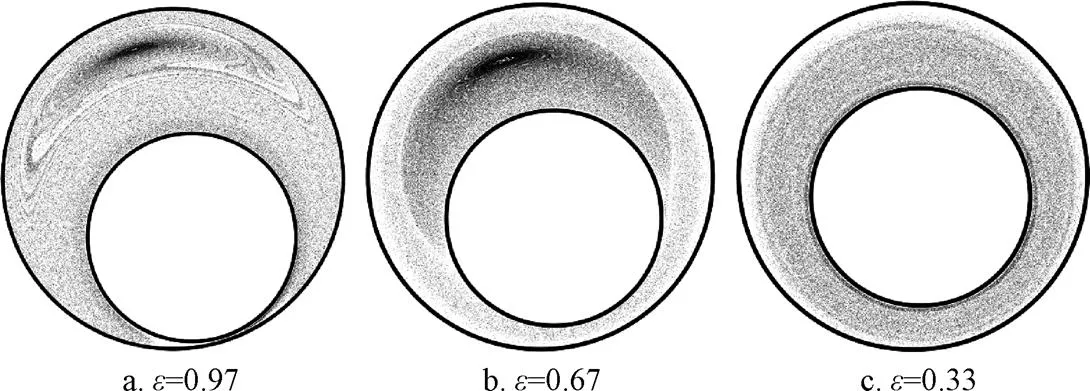
图8 混合器不同区域Poincaré截面

通过对不同周期月牙形区域的观察可以发现，月牙形区域内的粒子所形成的结构并非闭合的环状结构，也并非是准周期结构，而是螺旋源结构，并且具有一定的周期性：在偏心率为0.97时，为周期3，而在偏心率为0.67时，为周期6。周期越多则表明运动回归到初始位置附近区域相隔的周期越多，即粒子运动速度越慢，混合效率越低。此外，相比于二维偏心转子模型的研究结果[12]可知，在三维模型中，混合系统的流域内不存在被隔离的封闭环形结构，取而代之的是螺旋源结构，主要是由于三维流场的轴向扰动破坏了规则区内的结构，一定程度上使得非混沌区内物质交换更加频繁。

4.5 粒子可视化追踪

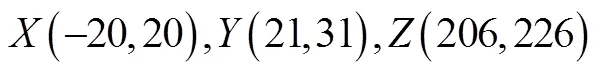
注：每幅图从上到下依次为t=0、t=T、t=2T、t=3T、t=4T、t=5T、t=10T和t=15T。

4.6 转子导程和偏心率对混合效率的影响

偏心螺旋转子的导程和偏心率是影响流场混合效率的重要参数。上述分析表明，转子的导程和偏心率对混合器的轴向和径向混合具有复杂的影响规律。为了分析转子导程和偏心率对混合效率的影响，分别选取转子导程=60、120和240 mm，偏心率分别为=0.97、=0.67和=0.33；采用剪切速率、对数拉伸、瞬时混合效率和平均时间混合效率等参数评价分散和分布混合特性[30]。初始时刻，在流域入口均匀释放20 000个虚拟流体质点，统计计算上述混合评价参数。

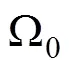
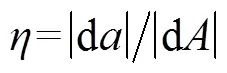
导程为60、120、240 mm不同偏心率混合器流体平均对数拉伸对比如图11所示，此时拉伸分布规律较为复杂。当导程为60 mm时，偏心率=0.97混合器流体的对数拉伸值最大，而偏心率为0.33混合器流体的对数拉伸值最小；这说明小导程偏心转子轴向拉伸较弱，主要依靠轴截面的径向拉伸作用，因此，增加偏心率可以增强材料的拉伸混合，提高混沌混合强度。当导程为120和240 mm时，偏心率为0.67混合器流体的对数拉伸值最大，此时流域中心的大部分流体处于拉伸状态，整体拉伸效果较好；而偏心率为0.33混合器流体的对数拉伸值最小，非混沌混合则占主导地位，主要依靠非混沌内回转区进行流体混合。

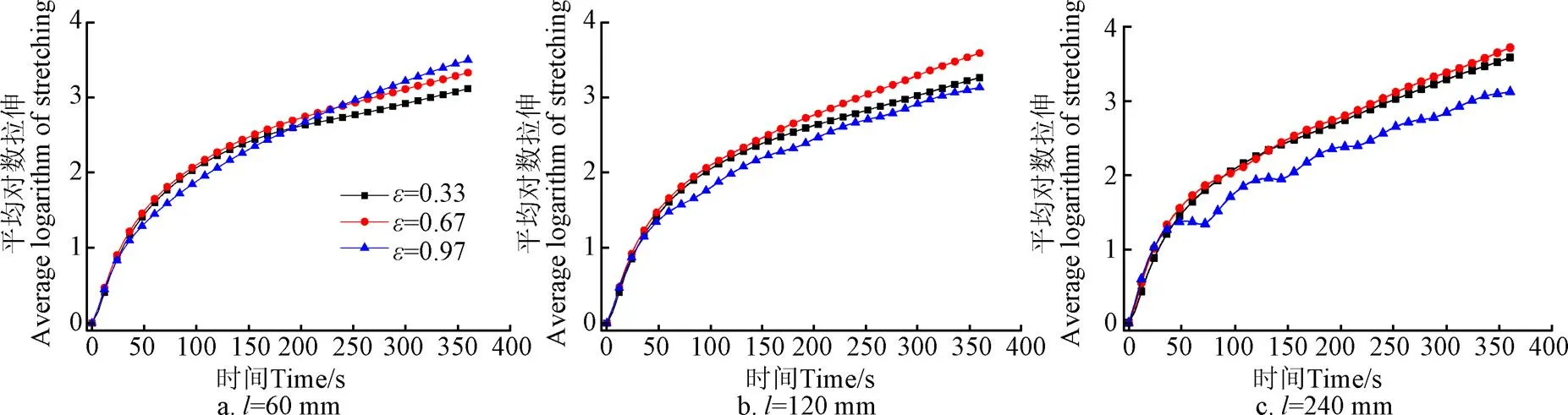
图11 不同导程和偏心率对平均对数拉伸的影响

瞬时混合效率即为局部某时刻的混合效率，可表述为[7]

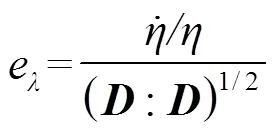
式中为瞬时混合效率。瞬时混合效率与局部能量耗散相关，其值范围[−1, 1]。

平均时间混合效率用来描述分布混合，平均时间混合效率随着混合时间的增加而下降，其表达式为[6]

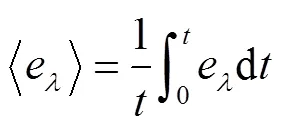
图12和图13分别为导程为60、120、240 mm时，螺旋转子偏心率对混合器内瞬时混合效率和时间平均混合效率的影响。从图12中可以看到，当导程为60 mm时，=0.97混合器流体的瞬时混合效率略大于=0.67和=0.33种情况。当导程为60和120 mm时，=0.97混合器流体的瞬时混合效率略小于=0.33情况，而=0.67的瞬时混合效率相对最大。且随着导程的增加，=0.97混合器瞬时混合效率的波动性增强，不稳定性增大。从图13中可以看到，当导程为60 mm时，=0.97混合器的时间平均混合效率略大于=0.67和=0.332种情况；当导程为60和120 mm时，=0.33混合器的时间平均混合最大，其次是=0.67，而=0.97混合器的时间平均混合最小，且随着导程的增加，三者相差逐渐增大。

从上述分析可以发现，转子的导程和偏心率对混合器的混合效率的影响规律较为复杂，难以直接确定混合性能相对较佳的导程和偏心率组合。对于本文研究的偏心转子食品混沌混合器，需要考虑高剪切应力对长分子链流体的剪切破坏作用，因此，更加侧重于拉伸流动以及拉伸混合效率。从拉伸流动角度来说，当导程=120 mm、偏心率=0.67时，混合器的具有相对较高的拉伸混合效率；当导程=60 mm、偏心率=0.33时，混合器的拉伸混合效率相对最低，但其剪切混合效率相对最高。当偏心率=0.33时，增加导程增加了混合器的轴向拉伸作用，可以提升混合效率；当偏心率=0.97时，增加导程却降低了混合器的混合效率。

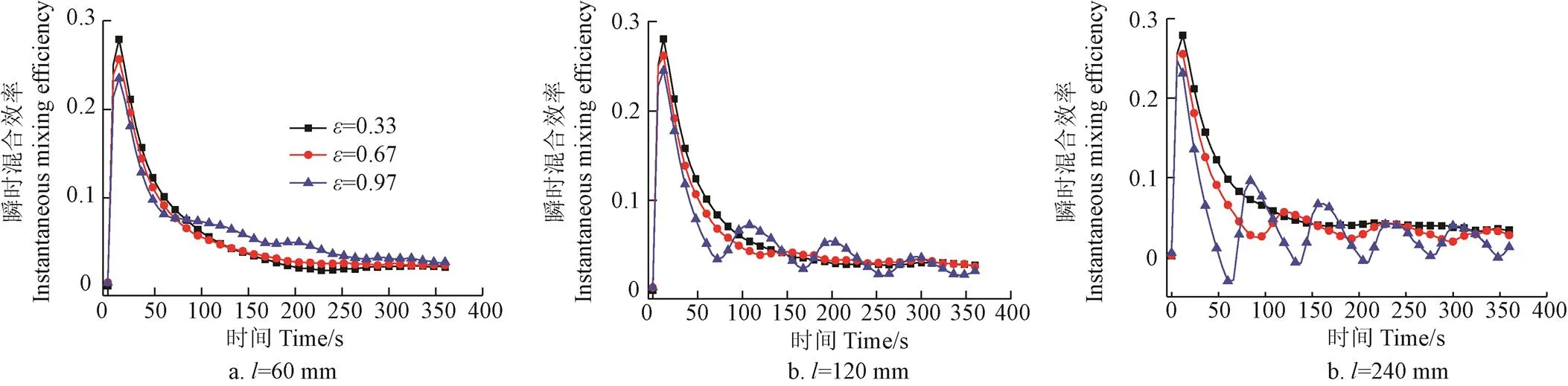
图12 不同导程和偏心率对瞬时混合效率的影响

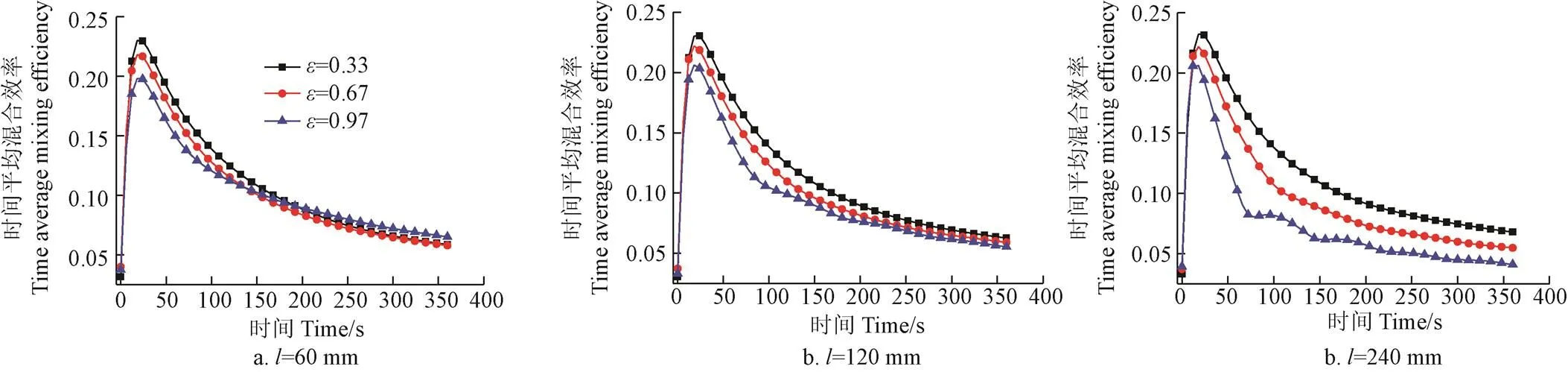
图13 不同导程和偏心率对时间平均混合效率的影响

5 结 论

从拉格朗日的新视角，利用FTLE和LCS，结合Poincaré截面，对螺旋式偏心转子面团混沌混合器的流体输运和混合机理进行了深入研究。利用LCS的准边界特性，分析了混沌混合器的混沌和非混沌区域分布规律；研究了螺旋式偏心转子的偏心率对混沌尺度以及非混沌区粒子运动特性的影响规律。

1）双曲LCS将混合器内流域划分为2个具有不同粒子运动特性的区域，即：沿筒壁做圆周运动的外螺旋区和在筒壁和转子之间较宽流域内做月牙状回转运动的内回转区。外螺旋区代表混合器流场的混沌区域，内回转区代表混合器流场的非混沌区域。

2）转子的偏心率对混合器流场的内回转区和外螺旋区分布具有重要的影响。由FTLE和Poincaré截面分析可知：偏心率较大时，外螺旋区的流体具有较强的混沌混合，随着偏心率的减小，外螺旋区的流体混沌混合逐渐减弱。另一方面，转子的偏心率较大时，混合器流场的内回转区混合强度较低，随着偏心率的减小，内回转区混合强度逐渐增加。

3）转子的偏心率对混合器流场的轴向速度也具有重要的影响。结合Poincaré截面和粒子可视化追踪可知：偏心率较大时，流场主要以外螺旋区的螺旋前进为主，轴向度较大。偏心率较小时，以内回转区运动为主，由于混合系统内转子扰动减小，轴向前进速度显著降低，但增强了混合器内回转区的径向混合。

通过对偏心螺转子混合器的剪切速率、对数拉伸、瞬时混合效率和平均时间混合效率的综合评价可知，从拉伸流动角度来说，当导程=120 mm、偏心率=0.67时，混合器的具有相对较高的拉伸混合效率；当导程=60 mm、偏心率=0.33时，混合器的拉伸混合效率相对最低，但其剪切混合效率相对最高。

[1] Song Y, Zheng Q. Dynamic rheological properties of wheat flour dough and proteins[J]. Trends in Food Science & Technology, 2007, 18(3): 132－138.

[2] 张金闯，刘丽，刘红芝，等. 食品挤压技术装备及工艺机理研究进展[J]. 农业工程学报，2017，33(14)：275－283.

Zhang Jinchuang, Liu Li, Liu Hongzhi, et al. Research advances on food extrusion equipment, technology and its mechanism[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(14): 275－283. (in Chinese with English abstract)

[3] Sudha M, Vetrimani R, Leelavathi K. Influence of fibre from different cereals on the rheological characteristics of wheat flour dough and on biscuit quality[J]. Food Chemistry, 2007, 100(4): 1365－1370.

[4] Zheng H, Morgenstern M, Campanella O, et al. Rheological properties of dough during mechanical dough development[J]. Journal of Cereal Science, 2000, 32(2): 293－306.

[5] Bellido G G, Scanlon M G, Page J H, et al. The bubble size distribution in wheat flour dough[J]. Food Research International, 2006, 39(10): 1058－1066.

[6] Connelly R K, Kokini J L. The effect of shear thinning and differential viscoelasticity on mixing in a model 2D mixer as determined using FEM with particle tracking[J]. Journal of Non-Newtonian Fluid Mechanics, 2004, 123(1): 1－17.

[7] Connelly R K, Kokini J L. Examination of the mixing ability of single and twin screw mixers using 2D finite element method simulation with particle tracking[J]. Journal of Food Engineering, 2007, 79(3): 956－969.

[8] 林江娇，赵春芳，朱立学. 双螺杆挤压膨化机温升特性的仿真分析与试验[J]. 农业工程学报，2012，28(16)：47－53.

Lin Jiangjiao, Zhao Chunfang, Zhu Lixue. Simulation analysis and experiment of temperature rising characteristics in twin-screw extruder[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2012, 28(16): 47－53. (in Chinese with English abstract)

[9] 孙智慧，徐克非，杨绮云，等. 食品双螺杆挤出机比能耗定量化研究[J]. 农业机械学报，2010，41(增刊)：225—228.

Sun Zhihui, Xu Kefei, Yang Qiyun, et al. Quantitative study on the specific energy consumption of food twin-screw extruder[J]. Transactions of the Chinese Society for Agricultural Machinery, 2010, 41(Supp.1): 225－228. (in Chinese with English abstract)

[10] 朱向哲，奚文. 三螺杆挤压机熔体输送段功耗特性的数值分析[J]. 农业机械学报，2009，40(5)：119－123.

Zhu Xiangzhe, Xi Wen. Simulation of power consumption characteristics in conveying element in triple screw extruder[J]. Transactions of the Chinese Society for Agricultural Machinery, 2009, 40(5): 119－123. (in Chinese with English abstract)

[11] Chella R, Ottino J M. Fluid mechanics of mixing in a single-screw extruder[J]. Industrial & Engineering Chemistry Fundamentals, 1985, 24(2): 170－180.

[12] ChienW L, Rising H, Ottino J. Laminar mixing and chaotic mixing in several cavity flows[J]. Journal of Fluid Mechanics, 1986, 170(9): 355－377.

[13] Hosseinalipour S M, Tohidi A, Shokrpour M, et al. Introduction of a chaotic dough mixer, part A: Mathematical modeling and numerical simulation[J]. Journal of Mechanical Science & Technology, 2013, 27(5): 1329－1339.

[14] Hosseinalipour S M, Tohidi A, Shokrpour M, et al. Experimental investigation of mixing in a novel continuous chaotic mixer[J]. Korean Journal of Chemical Engineering, 2014, 31(10): 1757—1765.

[15] Tian G, Wang M, Wang X, et al. Flow between eccentric cylinders: A shear-extensional controllable flow[J]. Korea-Australia Rheology Journal, 2016, 28(2): 139－148.

[16] Zambaux J A, Harion J L, Russeil S, et al. Combining two orthogonal secondary flows to enhance the mixing in an annular duct[J]. Chemical Engineering Research & Design, 2015, 94: 702－713.

[17] 宋海潮，徐幼林，郑加强，等. 脂溶性农药旋动射流混药器结构分析与混合均匀性试验[J]. 农业工程学报，2016，32(23)：86－92.

Song Haichao, Xu Youlin, Zheng Jiaqiang, et al. Structural analysis and mixing uniformity experiments of swirling jet mixer for applying fat-soluble pesticides[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(23): 86—92. (in Chinese with English abstract)

[18] Haller G. Lagrangian coherent structures[J]. Annual Review of Fluid Mechanics, 2015, 47: 137－162.

[19] Haller G. Lagrangian structures and the rate of strain in a partition of two-dimensional turbulence[J]. Physics of Fluids, 2001, 13(1): 3365－3385.

[20] Shadden S C, Lekien F, Marsden J E. Definition and properties of Lagrangian coherent structures from finite-time Lyapunov exponents in two-dimensional aperiodic flows[J]. Physica D: Nonlinear Phenomena, 2005, 212(3/4): 271－304.

[21] Robinson M J, Cleary P W. The influence of cam geometry and operating conditions on chaotic mixing of viscous fluids in a twin cam mixer[J]. AIChE Journal, 2011, 57(3): 581—598.

[22] Santitissadeekorn N, Bohl D, Bollt E M. Analysis and modeling of an experimental device by finite-time Lyapunov exponent method[J]. International Journal of Bifurcation and Chaos, 2009, 19(3): 993－1006.

[23] Miron P, Vétel J, Garon A. On the use of the finite-time Lyapunov exponent to reveal complex flow physics in the wake of a mechanical valve[J]. Experiments in Fluids, 2014, 55(9): 1－15.

[24] Bozorgmagham A E, Ross S D. Atmospheric lagrangian coherent structures considering unresolved turbulence and forecast uncertainty[J]. Communications in Nonlinear Science and Numerical Simulation, 2015, 22: 964－979.

[25] Prant S V. Chaotic lagrangian transport and mixing in the ocean[J]. The European Physical Journal-Special Topics, 2015, 223: 2723－2743.

[26] Green M A, Rowley C W, Smits A J. Using hyperbolic lagrangian coherent structures to investigate vortices in bioinspired fluid flows[J]. Chaos, 2010, 20: 017510.

[27] 赵学伟，魏益民，杜双奎. 挤压引起食品特性变化的数学模型研究综述[J]. 农业工程学报，2008，24(10)：301－307.

Zhao Xuewei, Wei Yimin, Du Shuangkui. Review on mathematical models of food property changes induced by extrusion[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2008, 24(10): 301—307. (in Chinese with English abstract)

[28] Wang C F, Kokini J L. Prediction of the nonlinear viscoelastic properties of gluten doughs[J]. Journal of Food Engineering, 1995, 25(3): 297－309.

[29] Avalosse T. Numerical simulation of distributive mixing in 3-D flows[J]. Macromolecular Symposia, 1996, 112(1): 91－98.

[30] Salahudeen S A, Alothman O, Elleithy R H, et al. Optimization of rotor speed based on stretching, efficiency, and viscous heating in nonintermeshing internal batch mixer: simulation and experimental verification[J]. Journal of Applied Polymer Science, 2013, 127(4): 2739—2748.

Analysis on influence of rotor lead and eccentricity on mixing flow field and efficiency of dough mixer

Zhu Xiangzhe, Gao He, Liu Jian

(,,113001,)

The chaotic food mixer with an eccentric spiral rotor is a new type of food processing device, in which the food fluids with long molecular chains can not be damaged by high shear stresses, such as traditional twin screw extruders. In fact, the previous researches had demonstrated that the food melt with high viscosity flowing in the food mixer has the nature of chaotic mixing. However, as a dynamic system of flow, the traditional Euler methods is difficult to distinguish the chaotic manifolds, which is a barrier for better understanding the mixing mechanism in the internal mixer. From a new viewpoint of 3D Lagrangian, the objective of our study is to explore the chaotic mixing mechanism in this new kind of food mixer under the disturbance of eccentric spiral rotor, to visually locate the poor and well mixing regions in the mixer and optimize the key geometric parameters of the eccentric spiral rotors. Firstly, a numerical simulation of the three-dimensional flow field in the food mixer is carried out using the mesh superposition technique (MST) and CFD code of Polyflow without considering the re-meshing for the periodical geometric changes. The Carreau-Yasuda constitutive model was used to describe the rheological behavior of the food material. Based on the transient velocity distributions, the finite time Lyapunov exponent (FTLE), Lagrangian coherent structure (LCS) and Poincaré section were calculated to analyze the fluid transport and mixing in the new chaotic food mixer with helical eccentric rotors. The LCS from the ridges of FTLE as a boundary was adopted to reveal the chaotic and regular zones in the mixer. And the particle tracking was used to illustrate the different fluid motions in the flow dynamic system based on the fourth-order Runge-Kutta scheme. Then the effects of rotor eccentric ratio on the chaos scale and particles motions in the regular of the mixer were studied, respectively. Moreover, based on the quantitative mixing measures, such as mixing shear rate, logarithmic of stretching, instantaneous mixing efficiency and average time mixing efficiency, the rotor lead and eccentricity rate were optimized to increase the mixing inefficiency of the chaotic food mixer. The results show that the hyperbolic LCSs divide into two regions with different particle motion characteristics for the food mixer, such as the inner rotary zone and the outer spiral zone. With the increase of rotor eccentric ratio, the strength of chaotic mixing in the outer spiral zone increases and that in the inner rotary zone decreases. When the rotor has little eccentric ratio, the mixing mainly depends on the fluid transport in the inner rotary zone. Then the axial velocity of fluid decreases significantly, but the mixing at radial direction of the inner rotary zone increases. Through optimization of the eccentricity and the lead distance of the eccentric rotor, it can be found that the mixer has relatively higher overall mixing efficiency with the lead of 120 mm and the eccentricity of 0.67, following is the lead of 60 mm and the eccentricity of 0.97, and the mixer has relatively poorer overall mixing efficiency with the lead of 60 mm and the eccentricity of 0.33. This paper has shown that the Lagrangian fresh perspective is more feasible than traditional Euler method in numerically investigate the evolution of two-dimensional mixing performance within a novel mixer. FTLE and LCS are useful tools for analyzing chaotic mixing flow in the mixer. This method provides new research ideas and theoretical basis for the design and optimization of food and other mixed equipment, which provides a better understanding the mixing mechanisms in a flow dynamic system.

mixer; food processing; flow fields; helical eccentric rotor; FTLE; lagrangian coherent structures; Poincaré section

10.11975/j.issn.1002-6819.2018.20.038

S224.23; TS203

A

1002-6819(2018)-20-0305-10

2018-05-17

2018-08-31

国家自然科学基金项目（51473073; 50903042）；辽宁省高等学校创新人才支持计划项目（LR2016022）

朱向哲，教授，博士，主要从事计算流体力学、非线性动力学以及流体力学非线性问题等领域研究。Email：xzzhu@126.com

朱向哲，高 鹤，刘 俭.转子导程及偏心率对面团混合器混合流场及效率影响分析[J]. 农业工程学报，2018，34(20)：305－314. doi：10.11975/j.issn.1002-6819.2018.20.038 http://www.tcsae.org

Zhu Xiangzhe, Gao He, Liu Jian. Analysis on influence of rotor lead and eccentricity on mixing flow field and efficiency of dough mixer[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(20): 305－314. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2018.20.038 http://www.tcsae.org