时滞对主动悬架幅频特性的影响

2018-10-19张进秋王兴野毕占东丁晓松

装甲兵工程学院学报 2018年4期

张进秋，王兴野，毕占东，丁晓松

(1. 陆军装甲兵学院车辆工程系，北京 100072； 2. 32142部队，河北保定 071000)

随着汽车行业的快速发展，人们对车辆的乘坐舒适性和行驶安全性提出了更高的要求，传统的被动悬架已难以满足实际需要，而主动悬架能够较大幅度地提高车辆的乘坐舒适性，是未来车辆悬架的发展方向[1-2]。时滞问题广泛存在于网络控制、电力、供应链、机器人控制等诸多领域[3-6]，是造成工程应用中控制效果难以达到预期甚至恶化的主要原因之一。然而，当前主动悬架振动控制算法设计的过程中较少考虑控制过程中的时滞问题，尽管有研究者[7-9]设计了针对控制输入时滞的主动控制算法，但大都缺少时滞对控制算法控制效果影响的分析。

为此，笔者在分析时滞对闭环控制系统影响的基础上，以2种典型的主动振动控制算法为例，分析时滞对悬架幅频特性的影响，并通过数值仿真进行分析与验证，以期为下一步考虑时滞的主动控制算法设计奠定基础。

1 时滞对闭环控制系统的影响

考虑时滞的闭环控制系统如图1所示。图中：GC(s)为控制器传递函数；u为主动控制力；Gp(s)为控制对象不含纯滞后的传递函数；xr为路面扰动；Gxr(s)为路面扰动的传递函数；d为控制时滞；R(s)为系统期望输出信号；Y(s)为系统实际输出信号。

根据图1可推导出，考虑时滞的闭环控制系统的实际输出Y(S)对R(S)和xr的传递函数分别为

(1)

(2)

其特征方程为

1+GC(s)Gp(s)e-ds=0。

(3)

由式(1)-(3)可以看出：时滞不仅使闭环系统控制力输出延迟，还使特征方程中出现了纯滞后项e-ds，这将影响闭环系统的稳定性。

2 考虑时滞的主动悬架系统建模

车辆的悬架系统通常可以简化为2自由度1/4车辆的主动悬架模型，如图2所示。

由图2可得到考虑控制输入时滞的动力学方程为

(4)

式中：ms为悬置质量(车体)；mt为非悬置质量(车轮)；ks、kt分别为悬架刚度和车轮刚度；t为时间；cs为阻尼器阻尼系数；xs、xt分别为车体和车轮的垂直位移。悬架模型参数设置如表1所示。

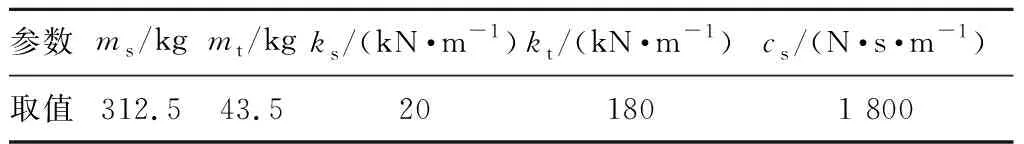
表1 悬架模型参数设置

3 时滞对2种典型振动控制算法幅频特性的影响

在不同类型的控制算法下，悬架性能的传递特性不同，本文以对低频振动有较好控制效果的天棚(Sky Hook，SH)主动控制和对中高频振动有较好控制效果的加速度阻尼(Acceleration Driven Damping，ADD)主动控制2种典型的控制算法[10]为例，分析时滞对悬架幅频特性的影响。

3.1 SH主动控制

SH主动控制的思想是假设车体与天棚之间装有一个阻尼器，其主动控制力u的计算方法为

(5)

式中：csky为天棚阻尼系数，此处csky=4 000 N·s/m。

尽管“道”是多义的，但其中有一条主线，即首先将“道”作为“物”，指一种特殊的存在体。它存在于形上领域，由其运动或者说在展开存在的过程中开出了天然现象之“物”。规律、准则或典范都是由这层含义的“道”延伸出来的。

(6)

(7)

(8)

式中：A1=css+ks；A2=mss2+css+ks+cskyse-ds；A3=mts2+kt。

分别取d=0，10，50，100 ms，利用式(6)-(8)绘制不同时滞条件下SH主动控制悬架性能传递特性曲线，并与被动无控制状态进行对比，结果如图3所示。可以看出：

1) 在低频区，SH主动控制能显著地降低车体加速度传递率的幅值，说明振动控制效果较好；

2) 不同时滞条件下,SH主动控制悬架性能传递特性曲线的二阶主振型基本相同，其中控制输入无时滞时系统的一阶主振型不是很明显，而有时滞时系统的一阶主振型振幅明显增大，且随着时滞的增大，在振动的高频区会出现多个共振峰；

3) 在SH主动控制下，悬架动行程的传递率有一定改善，但在低频共振区域车体加速度和车轮动载荷的传递率幅值明显增大，说明振动控制效果出现明显恶化，甚至出现劣于传统被动无控制状态的情况，这很有可能造成系统的失稳。

3.2 ADD主动控制

ADD主动控制的作用可理解为增大车身的质量，其主动控制力

(9)

式中：δ=0～1，为比例系数，此处取δ=0.6。

(10)

(11)

(12)

式中：A4=(1+δe-ds)mss2+css+ks。

分别取d=0，10，50，100 ms，利用式(10)-(12)绘制不同时滞条件下ADD主动控制悬架性能传递特性曲线，并与被动无控制状态进行对比，结果如图4所示。可以看出：

1) 除了车轮共振点之外的中高频区域，ADD主动控制能显著地降低车体加速度传递率的幅值，说明振动控制效果较好；

2) 不同时滞条件下,ADD主动控制悬架性能传递特性曲线的一阶主振型基本相同，而控制输入有时滞系统的二阶主振型振幅明显减小，且随着时滞的增大，在振动的高频区会出现多个共振峰；

3) 在ADD主动控制下，悬架动行程的传递率有一定改善，但在中高频区域车体加速度和车轮动载荷的传递率幅值明显增大，说明振动控制效果出现明显恶化，甚至出现劣于传统被动无控制状态的情况，同样很有可能造成系统的失稳。

4 仿真分析

为验证第3节的理论分析结果，以C级路面10 m/s速度下的随机振动作为系统的路面扰动输入，对不同时滞条件下悬架系统分别采用SH主动控制和ADD主动控制时的减振性能进行仿真分析。

根据式(4)，在MATLAB/Simulink中搭建系统的状态空间模型，并根据表1对悬架参数进行设置，仿真时间为40 s，则可得到被动无控制与不同时滞条件下SH、ADD主动控制悬架性能指标时域变化曲线对比，分别如图5、6所示，各条件下悬架性能指标统计结果分别如表2、3所示。为显示清晰，本文只截取了t=5～8 s时间段内的变化曲线。

条件车体加速度悬架相对动行程车轮相对动载荷均方根/(m·s-2)改善幅度/%均方根改善幅度/%均方根改善幅度/%被动无控制0.962 300.071 000.127 30SH主动控制(d=0 ms)0.834 613.270.068 53.640.135 4-6.34SH主动控制(d=10 ms)0.878 98.670.067 74.780.134 7-5.83SH主动控制(d=50 ms)0.894 17.090.066 95.900.132 7-4.26SH主动控制(d=100 ms)0.929 83.380.065 28.180.129 2-1.48

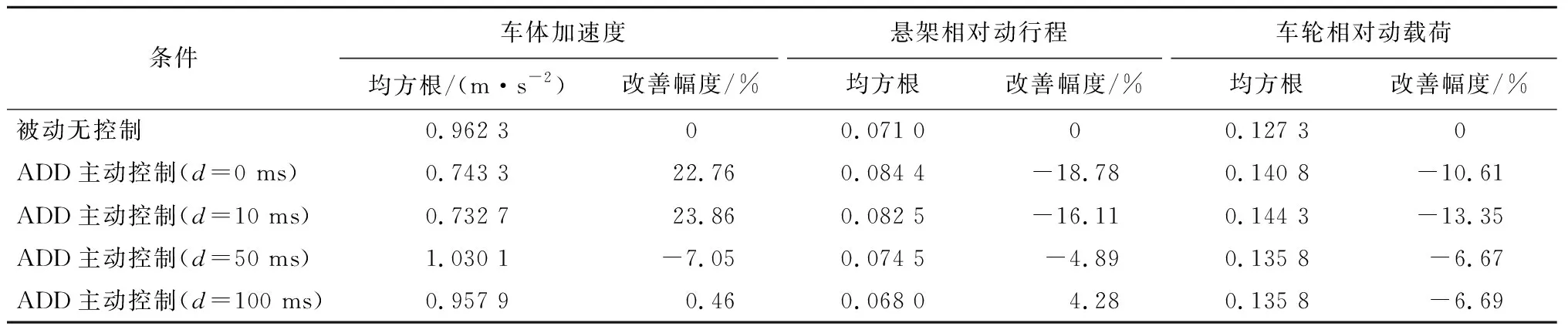
表3 被动无控制与不同时滞条件下ADD主动控制悬架性能指标统计结果

结合图5和表2可知：1)在SH主动控制下，即使是较小的时滞也会使车体加速度的控制效果恶化，且时滞越大，恶化越明显，当d=100 ms时，SH主动控制对车体加速度的改善效果只有3.38%，与被动无控制状态相差很小，失去了主动控制的优势；2)悬架相对动行程与车轮相对动载荷各有一定程度的变化，但其值均远小于1，可忽略其影响。

结合图6和表3可知：1)在ADD主动控制下，当不考虑控制输入的时滞时，控制算法对车体加速度有较好的抑制效果，且当时滞较小时，其对悬架性能控制效果的影响也相对较小,当d=50 ms时，对车体加速度的控制效果甚至比被动无控制状态还恶化了7.05%，而当d=100 ms时，对车体加速度的控制效果与被动无控制状态基本相当；2)悬架相对动行程和车轮相对动载荷虽有不同程度的恶化，但均在各自的许用范围之内，且都远小于1，可忽略其影响。