基于马尔科夫链的轻轨乘客轨迹预测新算法

彭 舰，孙 海，陈 瑜，仝 博，黄飞虎

(四川大学计算机学院 成都 610065)

近年来，中国城市轻轨交通系统得到了快速发展。在城市轻轨交通系统中，自动售票检票系统(auto fare collection, AFC)采集和记录了海量的乘客出行数据[1]。如何从这些数据中挖掘乘客的出行规律、出行轨迹模式等具有重要的研究价值。例如，通过对乘客出行轨迹的预测，运营商可以及时、快捷地制定针对紧急状况的应对措施、为乘客提供个性化服务、动态调整轻轨的发车频次；此外，还可以通过对乘客出行轨迹的精准预测制定轻轨广告投放策略，并可为新的交通网络设计提供决策支持。大多数研究[2-4]集中于对乘客出行目的地的预测，很少对乘客的出行轨迹进行预测。本文基于重庆市轻轨交通系统乘客的刷卡数据，提出一种基于马尔科夫链的乘客轨迹预测算法(light rail passenger trajectory prediction based on markov chain, LRPTPMC)，用于预测乘客下次出行轨迹。实验表明，该算法具有较好的预测效果。

1 相关研究

文献[5]基于公交IC卡数据，分别给出了由IC卡统计数据推算公交线路站点和区间出行站点的方法，并提出了基于GIS的公交IC卡数据分析处理系统框架，实现公交站点的推算；文献[6]提出了一种利用公交调度信息和智能卡刷卡信息来推断乘客上车站点的方法；文献[7]通过对北京市市民乘坐公交及地铁出行历史数据的分析，研究了乘客的个人出行模式。这些研究都是基于智能IC卡的数据，其关注点集中于公交站点及乘客个人的出行模式，未针对乘客下次出行轨迹进行预测。

在移动对象的轨迹预测方面，文献[2]基于地理和轨迹的语义特征预测移动对象下一时刻位置点信息，通过挖掘同类用户的常见行为特性来预测其未来位置；文献[3]提出基于状态的移动对象运动模型，并采用马尔科夫转移概率解释移动对象在不同状态间的转换；文献[4]采用混合马尔科夫链模型预测行人运动。然而，在这些已有的预测模型中，极大可能存在答案丢失[7]和精度依赖问题[8]。此外，这些研究均基于向量空间进行预测，无法预测具体的移动方向[9-10]。

因此，针对以上问题，本文主要针对城市轻轨交通系统中乘客的下次出行轨迹预测进行研究。

2 LRPTPMC：轻轨乘客轨迹预测算法

本节先给出相关参数定义和马尔科夫链模型，然后介绍轻轨乘客轨迹的预测算法。

2.1 相关定义

定义 2 连续轨迹。若当前的线路轨迹Gc的目的站点Sck与下次出行的轨迹Gn的出发站点Sn0相同，则称Gc和Gn是两条连续轨迹。

通过在真实轻轨交通数据集上的实验分析，乘客轨迹完整度取值大约为42.3%，由此可知，乘客的出行具有偏好返回特性。

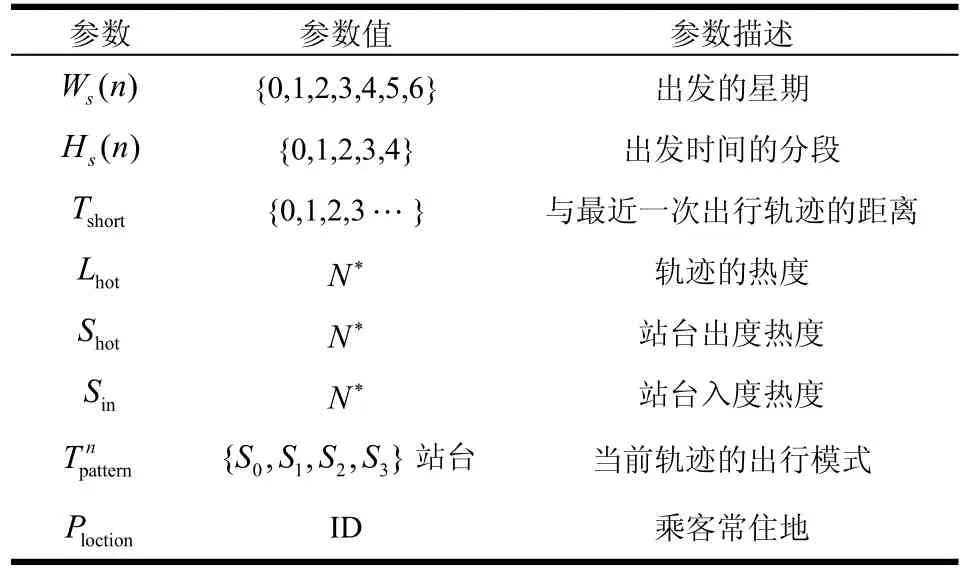
表1 参数列表

定义 5 乘客常住地。乘客刷卡记录中，出现次数最多的进站站点。

算法中参数说明如表1所示。

2.2 马尔科夫链模型

马尔科夫链模型认为用户下次出行的地点和之前去过的地点存在关联。MC模型中，用户的轨迹序列将构成该用户的n阶马尔科夫链，即用户u第i次访问的地点与该用户之前访问的n个地点存在关联关系，式(1)给出了其计算方法：

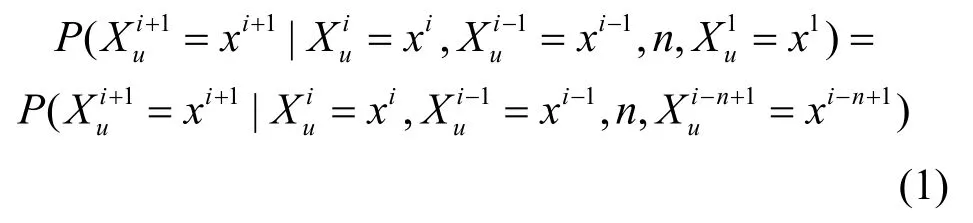
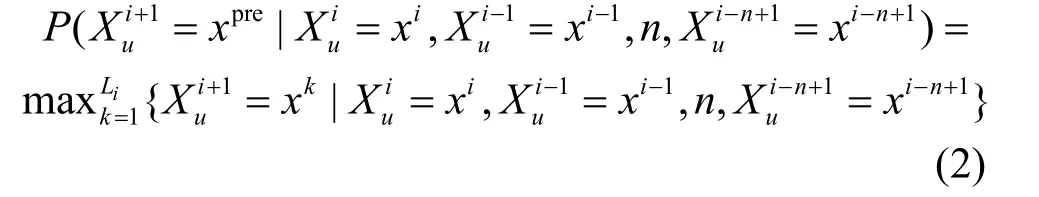
2.3 LRPTPMC预测算法描述

算法预测轻轨乘客出行轨迹分两个步骤：首先，利用贝叶斯分类器对乘客下次出行是探索新的轨迹，还是选择历史出行轨迹进行分类；然后，根据乘客最近一次出行轨迹与其常住地的关系，预测下次出行轨迹。

2.3.1 轨迹分类

根据朴素贝叶斯分类器，乘客轨迹可根据式(3)进行分类：

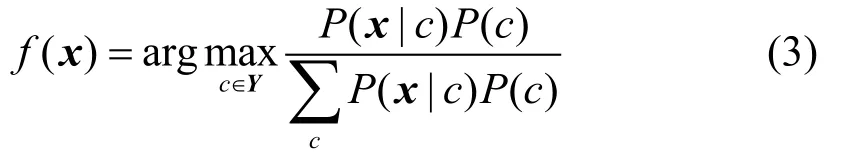
式中，x为特征向量，其中m为乘客历史轨迹的次数，n为历史不同轨迹的数量，p为历史不同轨迹的数量和历史轨迹的次数的比值，q为探索新线路的次数；Y为类别标记，Y={01}，，0表示乘客下次出行会探索新的轨迹，1表示乘客下次出行会选择历史出行轨迹。

2.3.2 轨迹预测

确定乘客下一次出行轨迹的分类之后，即可对乘客下一次出行轨迹进行预测。根据乘客最近一次出行轨迹与其常住地的关系，按以下4种情况预测其下次出行轨迹。

1)进站站台为常住地

算法首先判断最近一次出行轨迹是否为新的轨迹。如果是新的轨迹，就判断该乘客的值，当即出行模式为“”时，下次出行轨迹即是最近一次出行轨迹；当结合之前的数据分析，乘客的出行具有往返的特性，下次的出行则返回常住地。如果最近一次出行轨迹不是新的轨迹，即为历史轨迹时，首先构建该乘客出行轨迹的一阶马尔科夫状态转移矩阵，从状态转移矩阵中选取值最大的轨迹作为下次出行轨迹。

2)进出站台均不为常住地

当乘客最近一次出行轨迹的进站站台和出站站台均不为该乘客的常住地时，该乘客很可能处于中间状态，很难对其描述。该情形下，本文引入了轨迹状态转移矩阵，同时结合了时间、距离、线路热度等因素对其进行预测。

通过对重庆市轻轨数据的分析，发现在“中间状态”下，乘客下次出行轨迹的选择依赖于最近一次出行轨迹，同时也和出发的时间密切相关。表1中已将连续的时间处理成离散的数据。在实际生活中，乘客下次的出行与最近几次出行具有很强的相关性，为体现这种相关性，本文定义历史轨迹中的轨迹与最近一次出行轨迹的距离Tshort为：

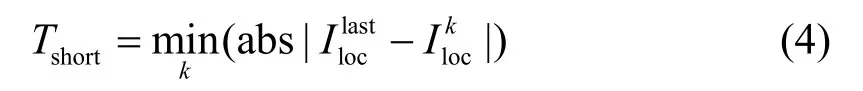
其中，

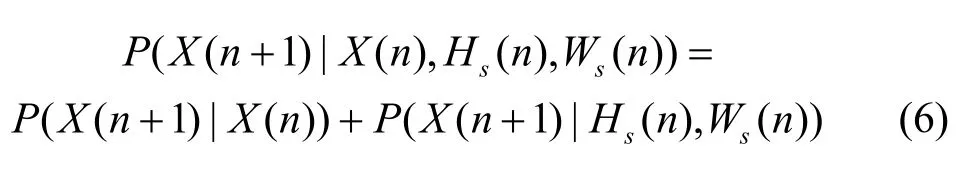
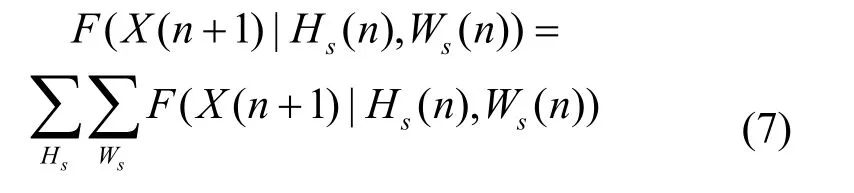
由式(6)和式(7)，式(5)可写为：

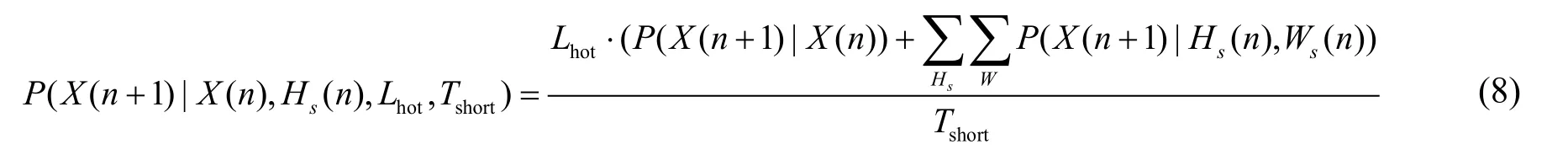
综上所述，当进出站台均不为常住地时，预测思路为：首先构建关于时间状态转移的一阶马尔科夫矩阵以及计算历史轨迹热度值。然后判断最近一次轨迹是否为新的轨迹，如果是，则下次的出行轨迹的进站时间为时间转移矩阵中最大的时间值，根据出行时间找到该出行时间段中热度值最大的轨迹作为下次出行轨迹；如果最近一次轨迹是历史轨迹中出现过的轨迹，则构建关于轨迹状态转移的一阶马尔科夫矩阵。最后依据式(8)计算每条历史轨迹的权值V，并选择取值最大的轨迹作为下次出行轨迹。

3)出站站台为常住地

当乘客最近一次出行轨迹中出站站台为常住地时，本文根据人类出行具有的最近相关性，引入了乘客的最近出行模式；同时，根据乘客出行的群集效应，引入了站台出度热度Sin，入度热度Sout以及轨迹热度Lhot。出度热度Sin和入度热度Sout的计算方法分别如下：

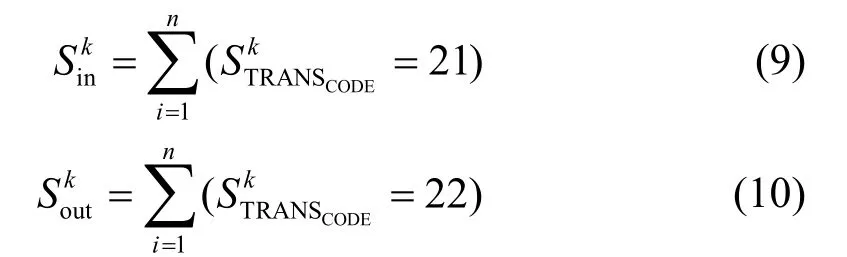
4)探索新轨迹

由于马尔科夫模型是基于历史轨迹对下次出行轨迹进行预测，不能有效解决乘客探索新轨迹的问题。因此，当预测到乘客下次的出行为探索新轨迹时，本文根据其他乘客的出行选择解决乘客探索新轨迹的问题。首先构建该乘客出行时间的状态转移矩阵，根据该矩阵来预测其下次出行的时间。然后根据这个出行时间，计算该时间段内所有乘客历史轨迹的Lhot值(不包括该乘客的历史轨迹)，预测的下次出行的轨迹即为Lhot值最大的轨迹。

3 实验及分析

3.1 实验环境和数据说明

本文的实验基于Spark集群(1台master，4台slave主机)。实验所用到的数据集是重庆市轻轨轨道交通系统中2014年12月1日—2015年5月31日的轻轨刷卡数据，表2给出了具体的数据描述。

原始数据集中包含444 743 582条刷卡记录，7 473 709位轻轨乘客。本节数据只保留了在这6个月内出行次数不少于100次的乘客的出行数据。

表2 数据集描述

3.2 数据预处理

3.2.1 数据格式介绍

本文所分析的数据是2014年12月—2015年5月共6个月的重庆市轨道交通的刷卡数据。该数据集包含了7 473 709个智能IC卡的共计444 743 582条的轨道交通刷卡记录，每条记录包含一次轻轨出行中乘客所搭乘轻轨的时间以及站台信息。主要包含的字段有：卡ID(TICKET_ID)、刷卡日期(TXN_DATE)、刷卡时间(TXN_TIME)、刷卡站台ID(TXN_STATION_ID)、卡类型(TICKET_TYPE)、进出站标志(TRANS_CODE)和换乘标识(TXN_AMT)等。

3.2.2 轨迹提取

刷卡记录是按照刷卡时间来记录的，数据可能存在记录错误和数据缺失问题。本文利用Spark框架对海量的数据进行了轨迹提取，过程如下：

1)创建一个CardID标识，初始值设为0，并将数据集按照日期和时间升序的原则进行排序。

2)访问最开始的记录，将CardID设为该记录的TICKET_ID的值，并检查TRANS_CODE字段的值；如果值为21，则进行步骤3)，如果值为22，则视此条记录为“脏记录”，并访问下一条TICKET_ID字段的值等于CardID的记录，重复步骤2)的工作。

3)存储记录中的TICKET_ID、TXN_DATE、TXN_TIME、TXN_STATION_ID字段的值后删除此条记录，并访问下一条TICKET_ID字段的值等于CardID的记录。

4)检查该记录中TRANS_CODE字段的值。如果值为22，则存储记录中的TICKET_ID，TXN_DATE，TXN_TIME，TXN_STATION_ID字段的值；如果值为21，则视此条记录为“脏记录”。最后删除此条记录，并访问下一条TICKET_ID字段的值等于CardId的记录，并重复步骤4)。

5)上述步骤中两次存储的记录就是卡ID为CardId值的乘客一次出行的完整轨迹，从步骤2)开始重复，直到访问到最后一条TICKET_ID字段的值等于CardId的记录，则可以得到卡ID为CardId值的乘客所有出行的完整轨迹。再将CardId的值设为0，重复步骤2)直到处理完全部记录。

3.3 算法评价指标

1)准确率和召回率

在本文中，准确率可以被视为预测精度，用于评价预测算法。公式如下：

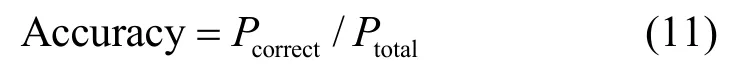
式中，Ptotal表示预测的总次数；表示预测正确的次数。

召回率计算公式如下：

2)F1分数

引入F1分数可以评价模型的综合性能，其计算公式如下：

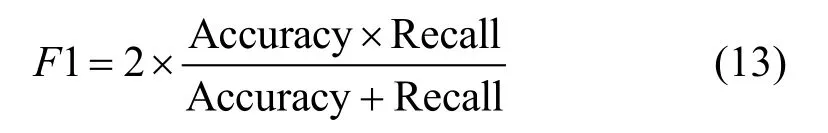
3.4 实验结果对比与分析

本文所用到的3个对比算法分别为LTMT、RNN及2-MC，其中LTMT为乘客历史轨迹中出现次数最多的线路(line of travel most times)；RNN为循环神经网络[11]；2-MC为二阶马尔科夫链，常用于目的地预测[12]。图1给出了预测精度测试对比结果。

由图1可知，本文的预测算法的预测精度明显优于其他3种算法，而随着乘客历史轨迹不同线路的增加，其预测精度也随之下降。其中RNN和2-MC的预测精度很相近，图中的离散点大致重合。

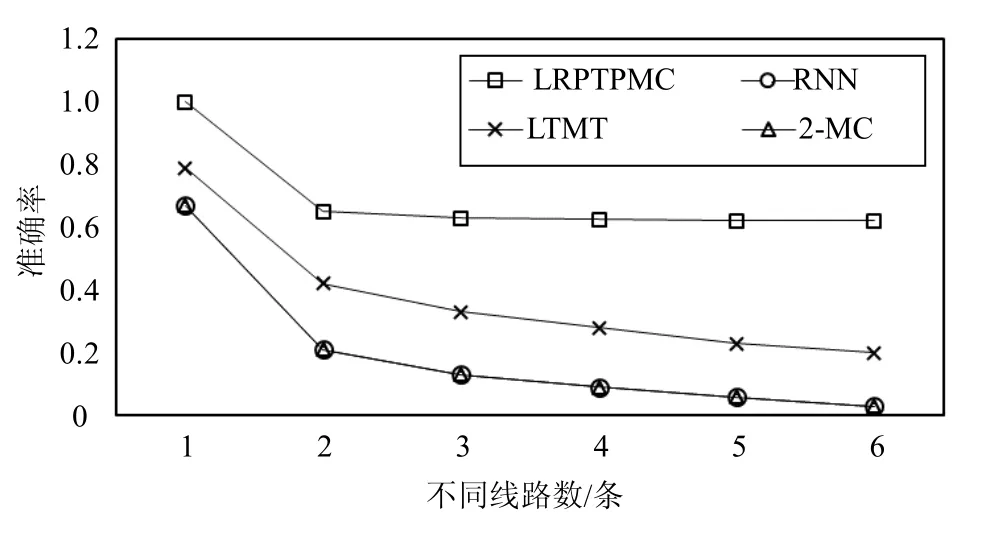
图1 预测精度对比图

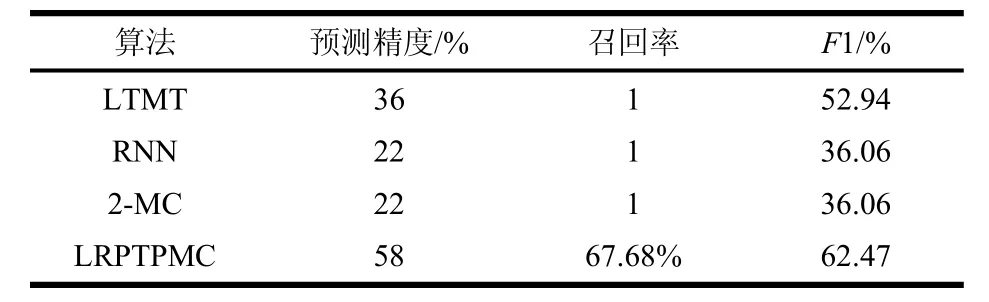
表3 算法对比

所有评价指标的对比如表3所示。根据图1和表3的结果可知，本文提出的LRPTPMC预测算法在精度、召回率和F1值等方面均优于其他3种常见算法。对于单一的二阶马尔科夫模型来说，其预测精度不及LRPTPMC算法的一半，说明本文的预测算法在马尔科夫模型基础上的改进有效。

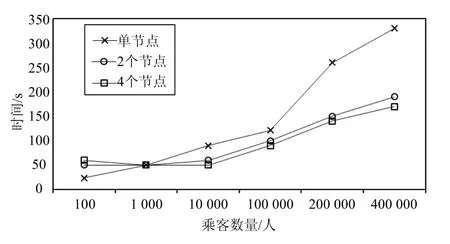
图2 运行时间对比

本文的实验基于分布式处理框架Spark，对预测算法进行了并行化处理。图2对比了单机环境下的算法和并行化算法进行运行时间。采用了6组数据，根据预测乘客的数量不同来体现运行时间的差异。如图2所示，当乘客数量规模大于1 000时，集群能有效利用其计算资源，能有效减少算法运算时间。

4 结束语

城市轻轨交通系统中采集和积累了海量的乘客出行数据。本文基于对重庆市轻轨交通数据的研究，提出了一种基于马尔科夫链的乘客轨迹预测(LRPTPMC)算法。实验结果表明，相比既有的预测算法，本文的LRPTPMC算法优于其他3个对比算法。同时利用分布式处理平台Spark来进行实验，极大地减少了实验运行时间。利用本文算法，可帮助轻轨运营管理者预测站台和轻轨流量，合理安排轻轨班次，改善轻轨交通服务。事实上，天气、影响力传播等因素也会对乘客出行产生影响，将这些因素融入轻轨乘客出行轨迹预测是本文下一步研究方向。