导数定义的极限模型在极限运算中的应用

杨艳兵

（常州机电职业技术学院 江苏常州 213164）

众所周知，导数概念牛顿、莱布尼兹等数学家在解决一些实际问题的过程中归纳、提炼出来的，是对客观世界中的某些数量关系的精辟描述，是微积分学中的重要基础概念。它对于数学学科乃至整个自然科学的发展都起到了至关重要的作用。在高等数学中，我们可以利用导数讨论函数的单调性、极值和最值以及其相关问题。高等职业院校学生对于利用基本初等函数的导数公式和求导法则计算各种类型函数的导数以及利用导数分析函数的性质掌握得比较好，但是他们往往对导数概念的具体极限形式理解模糊，且在利用导数解决一些问题的创造性思维上难以展开。学生存在这些问题的主要原因有两点：其一是教师在教学的过程中，对概念教学的认识不够，一味注重训练学生对于各种类型函数的导数计算，导致最后学生舍本逐末，竟不知导数为何物了；其二是高职学生对于导数的抽象定义形式有恐惧感，自然而然就不认识导数最初的面目了。本文主要是在复习导数定义的极限形式的基础上，给出其在极限运算中的一些应用。

1 函数在一点的导数定义的极限形式

函数在一点x0处的导数定义如下：

设函数 y=f( x)在点x0的某领域内有定义，当自变量在x0处有增量Δx时，函数相应地有增量Δ y = f( x0+Δ x) - f( x0)，如果极限存在，称函数 y=f( x)在点x0处可导，此极限值为函数y=f( x)在点x0处的导数，记为

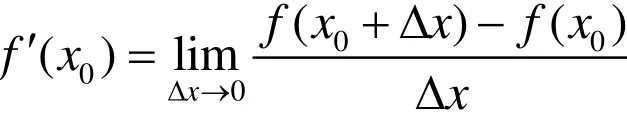
若令 x = x0+Δx ，则 Δ x = x - x0，当 Δx→0时， x→x0，于是函数 y=f( x)在点x0处的导数还可以记为：

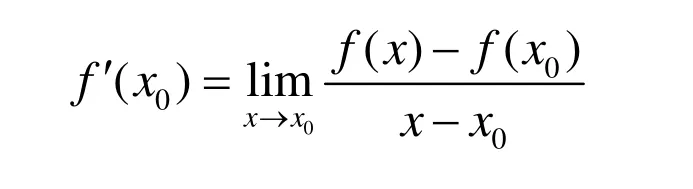
2 导数定义的极限形式在极限运算中的应用

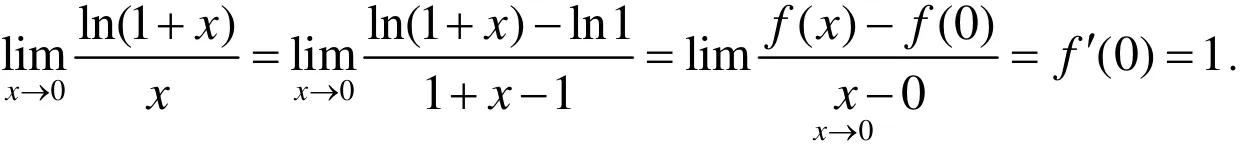
此外，通过分析可知，若令

关于第二重要极限一般都是用夹逼准则进行证明，这种证明方法比较复杂麻烦，且其原理对于高职学生来说也较难掌握。故此题中的极限求法，也是第二重要极限的一种比较简洁的证明。

分析：该极限与上一例题本是同根生，进行换元代换可以化为上一例题，但此题也可构造函数的导数形式，利用导数计算。

分析：在极限的运算中，该极限一般采用根式有理化的方式计算。但学生初次见到这个题目一般会有点懵，主要原因是一般的根式有理化中的题目一般都是比较具体的数字，如很少同时出现x和Δx。若是对函数的导数定义形式熟悉，此题也可另辟新径，下面的计算过程非常简单根据函数的导函数的极限形式

得

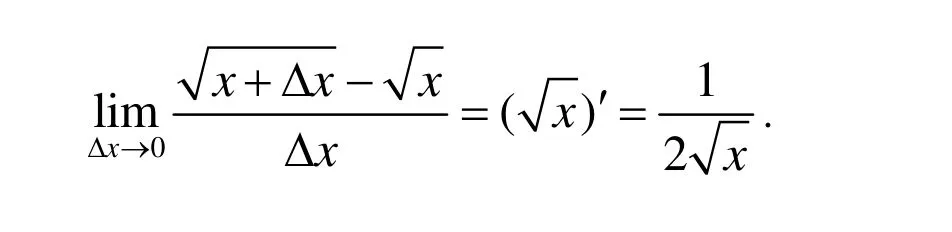
3 结语

根据导数的定义形式可知，导数的极限形式本质上是函数增量与自变量增量之比在自变量增量趋于零时的极限，故应用其求极限的本质就是根据要证明或计算的极限形式，构造某个具体函数的“增量之比”的极限，从而解决问题。

通过以上例题我们可以发现利用导数的定义来证明或计算一些极限，给学生一种耳目一新的体验，增加了一种新的计算极限的方法。同时也加深了学生对导数定义的极限形式的记忆和理解，拓展了导数在高等数学中的应用空间。