约束条件下的摆动喷管控制系统设计
2018-10-18余瑞星
王 敏,余瑞星
(1.西北工业大学 明德学院,陕西 西安 710124;2.西北工业大学 航天学院,陕西 西安 710072)
0 引 言
在现代战争中,弹道导弹是最具威胁的攻击性武器之一。弹道导弹的飞行过程可以分为3段:助推段、中段和再入段[1]。导弹在助推段飞行时,由控制系统作用,使导弹按照预定的飞行程序角(俯仰角)进入椭圆轨道。导弹获得满足射程所需的最优程序角后,保持此角不变,并使导弹升高和加速,直到发动机熄火为止[2]。从上述过程可以看出,基于姿态角的控制系统设计对弹道导弹完成助推段飞行任务意义重大。弹道导弹主要采用推力矢量控制(TVC)技术控制助推段的飞行姿态和弹道轨迹[3-4]。采用摆动喷管推力矢量控制装置的弹道导弹具有效率高、推力损失小的特点。摆动喷管的特殊工作模式给姿态控制系统的设计带来很多困难与挑战,许多学者对摆动喷管制技术进行了研究。文献[5]应用鲁棒回路法设计了导弹的纵向自动驾驶仪,在弹体自身及外界干扰因素不确定的情况下,该驾驶仪的设计满足了系统的性能指标要求。文献[6]将参数空间法和定量反馈理论应用于导弹飞行控制系统的设计中,当气动参数和摆动喷管控制误差有不同组合时,该系统表现出良好的稳定性和鲁棒性。文献[7]应用动态面法,设计了一种自适应滑模姿态控制律,保证了导弹非线性姿态控制系统在三通道耦合和模型气动参数不确定情况下的鲁棒性。
由燃料消耗、推力变化、弹道变化和级间分离等因素造成的导弹姿态运动参数时刻变化,这些参数对导弹的准确性和安全性造成一定影响[8]。基于摆动喷管控制的导弹姿态控制主要存在以下问题:弹道导弹在助推段飞行过程中受到外界干扰,模型存在不确定性。最优控制的输出调节器理论是将输出调节到零平衡点,但文中的控制系统需要跟踪的是不为零的输入指令,所以必须将输出调节器理论扩展到非零点。
针对上述问题,文中拟采用最优控制理论,来解决姿态控制中模型不确定、运动参数时变和非零点输出调节的问题。
1 弹道导弹数学模型
1.1 摆动喷管推力及力矩
为了方便描述摆动喷管运动所产生的推力和力矩,根据弹体坐标系Oxyz,建立喷管坐标系O1x1y1z1,其中,O1为喷管坐标系原点,位于摆动喷管的回转中心;x1轴与弹体坐标系的x轴重合,指向头部为正;y1轴在弹体纵向对称平面垂直于x1轴,向上为正;z1轴垂直于x1o1y1平面,方向用右手法则确定[9]。将推力矢量投影到喷管坐标系上如图1所示。
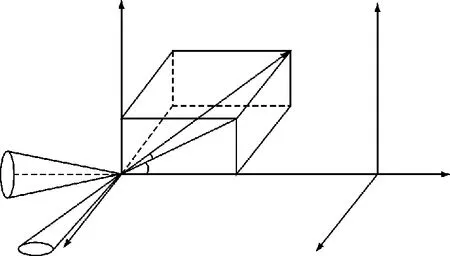
图1 推力在喷管坐标系的投影Fig.1 Projection of thrust onto nozzle coordinate system
受力分析结果如下
Px1=Pcosδy1cosδz1
Py1=Pcosδy1sinδz1
Pz1=-Psinδy1
(1)
推力产生的力矩为
Mxp=0
Myp=Pz1(xR-xT)
Mzp=-Py1(xR-xT)
(2)
式中P为发动机平均推力,N;δy1为推力与xoy平面的夹角,(°);δz1推力在xoy平面投影与x轴的夹角,(°);xR,xT分别为弹体理论尖端与喷管回转中心位置和弹体质心位置之间的距离,m.
由式(1)可知,夹角δy1对导弹纵向和横向的受力都有影响,只要夹角δy1存在,纵向通道和横向通道就有耦合作用,两通道控制系统必须增加解耦措施,才能独立设计。显然上述情况给控制系统的设计增加了一定的难度。为避免纵向通道和横向通道产生耦合效应,简化控制系统设计,特提出等效舵偏角的概念,以期望达到两通道单独控制的目的,其中δy用于偏航通道,控制导弹的横向运动;δz用于俯仰通道,控制导弹的纵向运动;k为舵分配系数。基于等效舵偏角,以舵偏角偏转方向为正,摆动喷管产生的推力在喷管坐标系的投影如图2和图3所示。

图2 推力在纵向平面的投影Fig.2 Projection of thrust onto longitudinal plane
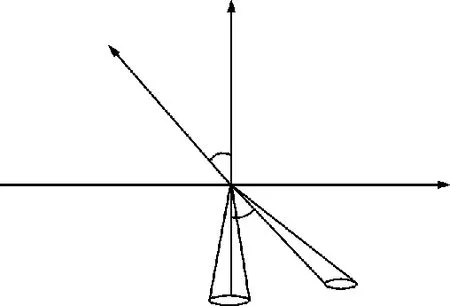
图3 推力在横向平面的投影Fig.3 Projection of thrust onto transverse plane
受力分析结果如下[10]
Px=Pkcosδz+P(1-k)cosδy
Py=Pksinδz
Pz=-P(1-k)sinδy
(3)
经推导公式(1)和(3),得到等效舵偏角的分配关系,如式(4)所示。
(4)
至此,导弹纵向通道和横向通道可独立设计控制系统,完成姿态角跟踪的任务。
1.2 导弹纵向动力学模型
对于轴对称的弹道导弹而言,其俯仰通道和偏航通道的运动特性是一致的,因此设计姿态控制系统时,仅设计俯仰通道控制系统即可,偏航通道控制系统可完全参考俯仰通道控制系统结构[11]。于是文中选取某弹道导弹助推段的俯仰通道为研究对象,并利用短周期运动方程来近似表示弹体纵向动力学。其状态空间表达式为
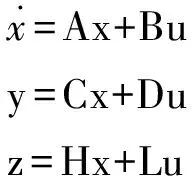
(5)
式中 状态变量x=[ωzαθ]T,输入u=δz,输出y=[ωzαθ]T,z为输出的一部分;A为系统矩阵;B为输入矩阵;C为输出矩阵;D为状态转移矩阵,其中θ=ωz,因此A阵的第三列全为零。
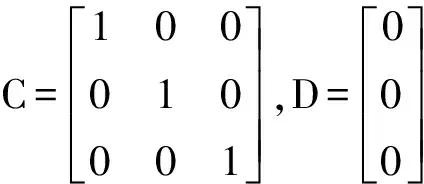
H=[0 0 1],L=[0]

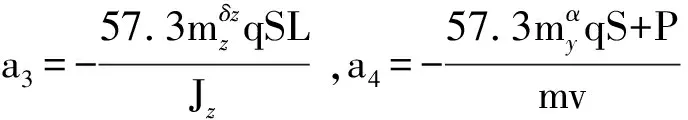
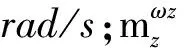
2 姿态控制系统设计
2.1 线性二次型输出调节器问题
一般线性二次型输出调节器问题的目标函数为[15]
(6)

其最优控制为
u=Koptx=-R-1(BTP+ST)x
(7)

P是满足式(8)的黎卡提代数方程的半正定解[16]
A′TP+PA′-PRB-1BTP+Q′=0
(8)
各参量表示如下
A′=A-BR-1ST,Q′=Q-SR-1ST
2.2 姿态指令跟踪器设计
(9)
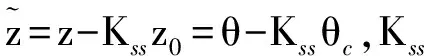
该函数物理意义是:在消除指令偏差足够快和控制输入足够小的性能指标约束下,求解最优控制,使控制系统稳定跟踪输入指令[18]。
此时的状态方程模型为
(10)
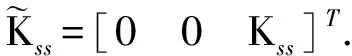
跟踪器问题和调节器问题具有相同的反馈增益解,因此Kopt可参照上述调节器问题确定[19]。考虑到文中状态方程模型中,矩阵D为零,矩阵C为单位阵,所以系统的输出反馈可以化为状态反馈,即此时的控制输入为
求解得,
(11)
为确定稳态误差增益Kss,将式(11)代入模型(10),系统的状态方程化为以俯仰角指令为输入、执行俯仰角为输出的形式,即
(12)
式中Ac=A+B[I-KoptD]-1KoptC
Cc=H+L[I-KoptD]-1KoptC
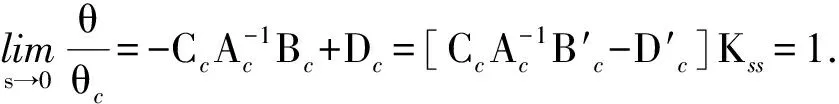
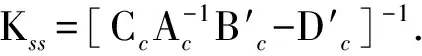
至此,控制系统的增益系数全部被确定,则该姿态指令跟踪器的最优控制为
(13)
由式(13)的反馈控制方式可知,文中姿态控制系统结构为经典三回路结构,详细框图如图4所示。

图4 姿态控制系统结构框图Fig.4 Attitude control system structure diagram
应用最优控制理论设计控制律可以达到系统的性能指标要求,却没有考虑系统在参数不确定和高频衰减等情况下的鲁棒性,那么所设计的控制律在实际系统中应用时可能出现系统不稳定的情况[21]。为了避免上述情况发生,可以利用经典控制理论的频域约束条件限制权系数的选取,直至系统满足稳定性指标。在选择权系数时,应在穿越频率足够小和稳定裕度足够大的基础上,尽可能降低对控制量的需求,提高系统的响应速度。
3 仿真及分析
选取特征点对导弹纵向通道和横向通道控制系统进行定点仿真校验,特征点的初始高度为2km,初始条件、权系数和控制增益的取值见表1,仿真结果如图5~8所示。

表1 特征点仿真参数
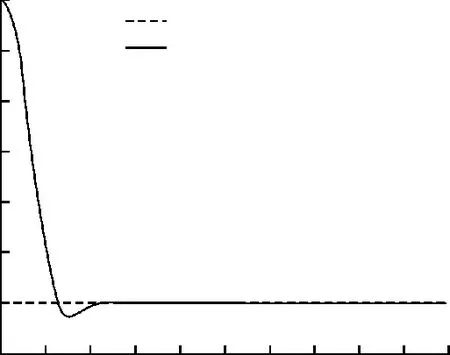
图5 俯仰角指令跟踪曲线(特征点1)Fig.5 Pitch angle tracking curve(Feature point 1)
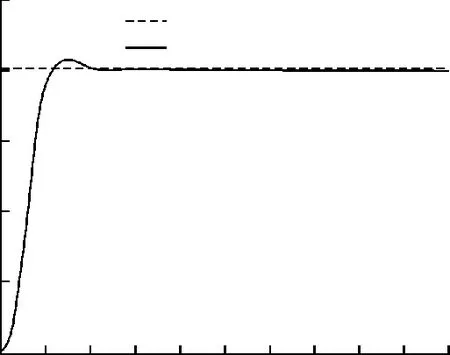
图6 偏航角指令跟踪曲线(特征点1)Fig.6 Yaw angle tracking curve(Feature point 1)
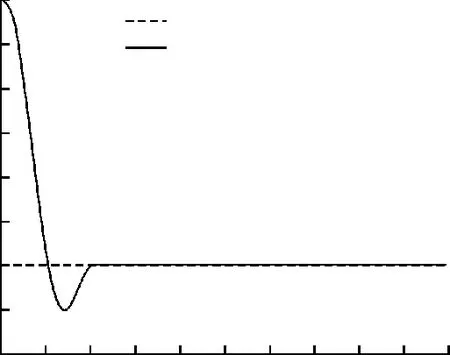
图7 俯仰角指令跟踪曲线(特征点2)Fig.7 Pitch angle tracking curve(Feature point 2)
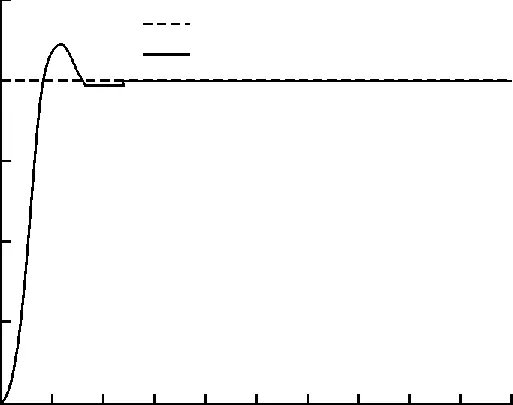
图8 偏航角指令跟踪曲线(特征点2)Fig.8 Yaw angle tracking curve(Feature point 2)
从图5~图8可以看出,不同特征点处,通过调节权系数取值,可以实现系统输出对输入的快速准确响应,但在马赫数升高,气动数据变得更加复杂的情况下,控制系统的超调量明显增大。
导弹气动参数摄动会引起模型的变化,一般情形下,导弹气动参数中动导数偏差可达50%以上,静导数偏差可达15%~20%.为进一步校验系统的鲁棒性,需要对气动系数进行拉偏处理。假定气动系数在特征点1,2处分别有±50%的变化,仿真结果如图9~12所示。

图9 气动摄动对俯仰角的影响(特征点1)Fig.9 Influence of pneumatic perturbation on pitch angle(Feature point 1)
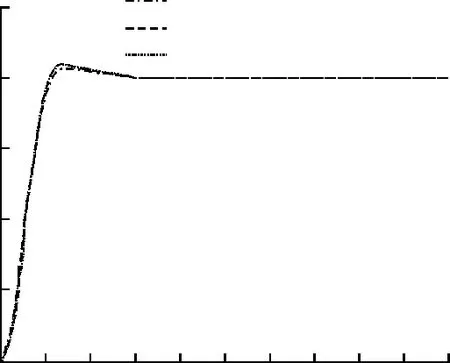
图10 气动摄动对偏航角的影响(特征点1)Fig.10 Influence of pneumatic perturbation on yaw angle(Feature point 1)
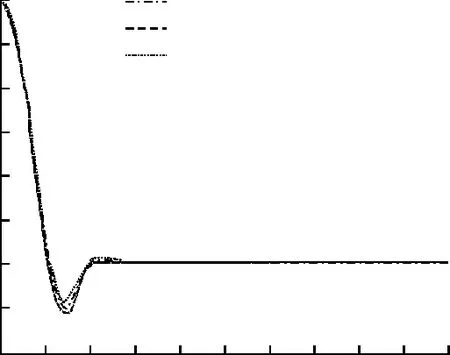
图11 气动摄动对俯仰角的影响(特征点2)Fig.11 Influence of pneumatic perturbation on pitch angle(Feature point 2)
由图9~12可见,考虑了气动参数不确定性的系统依旧保持稳定,能准确跟踪俯仰角和偏航角指令,不过在响应过程中,控制系统的超调量和响应时间略有变化,对气动进行+50%拉偏的控制系统超调量增加,响应速度变快,对气动-50%拉偏的控制系统超调量减少,响应速度变慢。
4 结 论
1)运动参数时变的弹道导弹,以摆动喷管作为控制装置,采用现代控制理论设计的控制系统,不但能够保证系统的稳定性,还能以较小误差快速地跟踪系统的俯仰角和偏航角指令;
2)该系统在气动参数摄动±50%的情况下,仍然可以保持稳定,完成姿态指令跟踪的任务,保证了系统的鲁棒性。
