一种模块化多电平直流输电线路单端保护原理

2018-10-18高淑萍胡振宇张保会宋国兵

西安科技大学学报 2018年5期

高淑萍，胡振宇，高悦，张保会，宋国兵

(1.西安科技大学电气与控制工程学院，陕西西安 710054；2.西安交通大学电气工程学院，陕西西安 710049)

0 引言

模块化多电平换流器(Modular Multilevel Converter，MMC-HVDC)采用了子模块(Sub-Module，SM)串联的方式输出多电平阶梯波，具有扩展性好、输出波形质量高、开关频率低等优点，在柔性输电、直流配电等领域具有广阔的应用前景[1-4]。近几年，模块化多电平直流电网相关技术在我国快速发展，电力电子相关技术在煤矿供电领域也得到了应用[5]。此供电方式有望用于煤矿供电系统，提升煤矿供电系统的先进性和安全性。

目前，对模块化多电平换流器直流输电系统的研究主要集中在控制策略和拓扑结构方面，对直流线路故障保护方面的研究较少。

在控制策略的研究方面，文献[6]建立了MMC-HVDC的数学模型，提出了控制策略，并在此基础上简化了MMC-HVDC的等效电路图。文献[7]将柔性直流输电系统的控制系统进行了分级，分为系统级控制、换流器级控制、阀级控制。文献[8]通过分析造成MMC子模块电容电压不均衡的原因，为MMC-HVDC提出了一种电容电压均衡控制策略，降低了开关器件的开关频率及MMC损耗。文献[9]提出了一种无需负序坐标变换和相间解耦环节的MMC通用环流抑制策略，实现对MMC环流的有效抑制。文献[10]研究了对MMC使用最近电平逼近调制方式，说明了换流器的调制计算量要尽可能的小，才能使控制的周期缩短，从而得到高质量的波形输出。文献[11]提出了在MMC-HVDC系统发生双极短路故障的情况下，系统重合闸的控制策略。文献[12]提出了基于通用的双闭环矢量控制策略，通过将实际电路元件的特性映射入控制系统来抑制故障过电流；在拓扑结构研究方面，文献[13]重新设计了子模块的拓扑结构，抑制了直流侧的故障电流。文献[14]对原有MMC子模块进行改进，通过在子模块出口添加反并联晶闸管，使其具有故障清除能力；文献[15-16]提出了新的双钳位子模块拓扑结构，构造了一种新型的混合拓扑结构，但是仍不能解决子模块电容出现的并联耦合问题；文献[17]通过采用全桥拓扑结构的方法，实现了电流的阻断能力，但是存在器件过多问题。文献[18]改进了MMC半桥型拓扑，设计双子模块串联的拓扑结构，使得故障恢复速度变快。在故障保护研究方面，文献[19]从技术和经济的角度说明了需要在故障发生的初期阶段即故障电流的上升阶段就检测出故障，对故障检测速度提出了很高的要求。文献[20]提出了一种冗余保护策略，可以使MMC-HVDC系统在一个或少数几个子模块故障的情况下保持正常运行。文献[21]通过估算直流线路电流的初始上升速率，来快速定位故障，但只讨论了双极短路故障。

文中利用在直流线路两端串联小电感的电压，应用故障分量分析法，分析研究了双端±50kV MMC-HVDC系统直流线路可能出现的各种短路故障，提出了一种仅利用一端换流站的正、负极串联小电感的电压就可以实现直流输电线路的保护原理。该保护原理仅利用一端换流站正、负极串联小电感的电压故障分量的极性识别故障极；利用该端正、负极串联小电感的电压故障分量的变化速率的快慢，构造相应的判据，可以实现区内、外故障的识别。最后利用PSCAD暂态仿真软件，建立了双端 ±50kV MMC-HVDC输电系统模型，用以输出故障数据，并利用Matlab进行保护算法验证，仿真结果验证了故障分析及保护方法的正确性和有效性。

1 MMC-HVDC的故障特性分析

图1为双端MMC-HVDC系统结构简图。图1中MMC1和MMC2两个换流站均采用模块化多电平换流器拓扑结构，换流站的正、负两极均由电缆连接，L为直流线路加入串联电感。P1L和P1R为MMC1换流站正极附加小电感两侧的2个测量点，N1L和N1R为MMC1换流站负极附加小电感两侧的2个测量点，P2L和P2R为MMC2换流站正极附加小电感两侧的2个测量点，N2L和N2R为MMC2换流站负极附加小电感两侧的2个测量点。

图1 双端MMC-HVDC输电系统Fig.1 Two terminal MMC-HVDC system

图1中，故障位置及故障类型见表1.

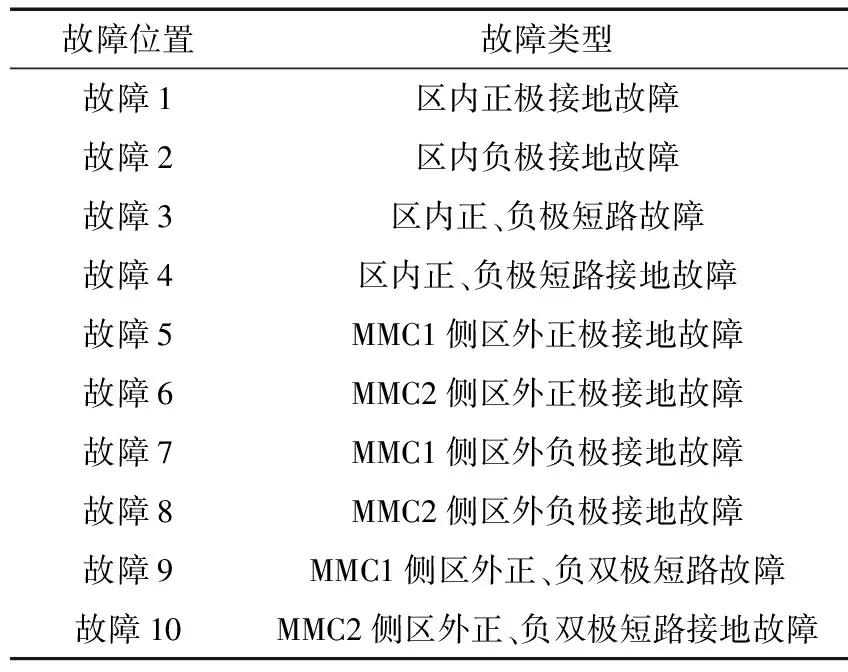
表1 故障位置及故障类型

在表1中，故障1，2，3和4为区内故障，故障5，6，7，8，9和10为区外故障。

1.1 故障网络电压故障分量极性分析

系统发生故障的初始阶段，可以近似认为系统还是线性的，因此由叠加原理可知，故障状态可以等效为非故障运行状态和故障附加状态的叠加，下面将对其故障附加状态进行分析。

1.1.1 单极故障的故障网络

MMC-HVDC系统单极故障网络附加图如图2所示。

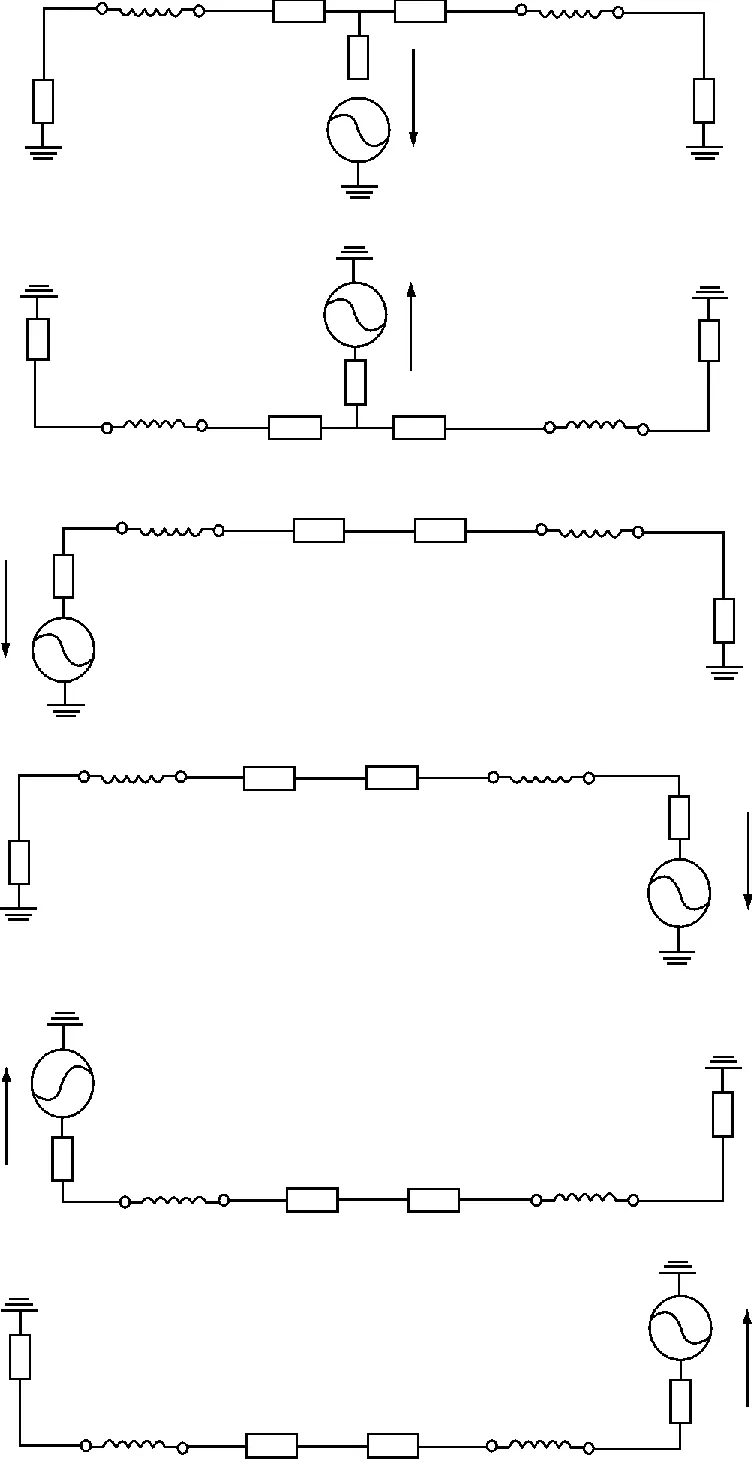
图2 单极故障的故障状态网络Fig.2 Fault state network diagram of single electrode failure

图2中，(a)、(b)、(c)、(d)、(e)和(f)分别为故障1，2，5，6，7和8的故障附加状态等效电路图，uf表示故障点对地电压，Z1，Z2，Z3和Z4分别代表两边交流侧等效阻抗，ZP1，ZP2，ZN1和ZN2分别为线路到故障点等效阻抗。

由图2(a)可以看出，当MMC-HVDC系统直流线路发生区内正极故障，P1L，P1R，P2L和P2R4个点的电压均应下降，因此P1L，P1R，P2L和P2R4个点处的电压故障分量的极性均为负，同理可由图2(c)和(d)看出，当MMC-HVDC系统直流线路发生区外正极故障时，P1L，P1R，P2L和P2R4个点处的电压故障分量的极性也均为负。

由图2(b)可以看出，当MMC-HVDC系统直流线路发生区内负极故障，N1L，N1R，N2L和N2R4个点所测量的电压均应上升，因此N1L，N1R，N2L和N2R4个点处的电压故障分量的极性均为正，同理可由图2(e)和(f)看出，当MMC-HVDC系统直流线路发生区外负极故障时，N1L，N1R，N2L和N2R4个点处的电压故障分量的极性也均为正。

由上述分析可知，当MMC-HVDC系统直流线路发生正极故障时，P1L，P1R，P2L和P2R4个点处的电压故障分量的极性均为负，而由于MMC-HVDC系统直流线路正、负两极的耦合作用，N1L，N1R，N2L和N2R4个点处的电压故障分量的极性也均为负；而当MMC-HVDC系统直流线路发生负极故障时，N1L，N1R，N2L和N2R4个点处的电压故障分量的极性均为正，而由于MMC-HVDC系统直流线路正负两极的耦合作用，P1L，P1R，P2L和P2R4个点处的电压故障分量的极性也均为正。

1.1.2 双极故障的故障网络

MMC-HVDC系统双极故障的故障网络附加状态图如图3所示。

图3(a)、(b)、(c)和(d)分别为故障3，4，9和10的故障附加状态等效电路图。由图3(a)可以看出，当MMC-HVDC系统直流线路发生区内双极故障，P1L，P1R，P2L和P2R4个点所测量的电压均应下降，因此P1L，P1R，P2L和P2R4个点处的电压故障分量的极性均为负，N1L，N1R，N2L和N2R4个点所测量的电压均应上升降，因此N1L，N1R，N2L和N2R4个点处的电压故障分量的极性均为正。同理，由图3(b)、(c)和(d)看出，当MMC-HVDC系统直流线路发生双极故障时，P1L，P1R，P2L和P2R4个点处的电压故障分量的极性均为负，N1L，N1R，N2L和N2R4个点处的电压故障分量的极性均为正。

图3 双极故障的故障状态网络Fig.3 Fault state network diagram of double electrode failure

综上所述，当MMC-HVDC系统直流线路发生正极故障时，P1R和N1R2个点处的电压故障分量的极性相同且均为负，如故障1，5和6；当MMC-HVDC系统直流线路发生负极故障时，P1R和N1R2个点处的电压故障分量的极性相同且均为正，如故障2，7和8；当MMC-HVDC系统直流线路发生双极故障时，P1R和N1R2个点处的电压故障分量的极性不同。

1.2 故障网络电压故障分量变化量分析

由图2(a)可以看出，保护区内与区外被电感相隔开，当MMC-HVDC直流线路发生区内正极故障时，P1R点处的电压迅速下降，所以该点处电压故障分量也迅速向负极性增大，流过串联小电感的电流迅速增大，于是电感产生一个感应电压，所以除发生接地故障的正极区外，其余测量点的电压故障分量虽然也会向负极性增大，但变化速率要慢得多，因此，N1R处电压故障分量的变化速率要远小于点P1R处的电压故障分量的变化速率。

由图2(c)可以看出，当MMC-HVDC直流线路发生MMC1侧区外正极故障时，P1L点处的电压迅速下降，而P1R点与N1R点都被电感相隔开，所以P1R点与N1R点处电压故障分量的变化速度要远小于P1L点处的电压故障分量的变化速度，但P1R点与N1R点处电压故障分量的变化速率几乎相同。而MMC2侧区外正极故障则与MMC1侧区外正极故障类似，P1R点与N1R点处电压故障分量的变化速率几乎相同。

同理可知，当MMC-HVDC直流线路发生区内负极故障时，P1R处电压故障分量的变化速率要远小于点N1R处的电压故障分量的变化速率；而发生MMC1侧区外负极故障和MMC2侧区外正极故障时，P1R点与点N1R处电压故障分量的变化速率几乎相同。

因此，当通过P1R处电压故障分量与N1R处电压故障分量极性判断出该故障为正极故障或者负极故障后，再通过判断P1R点与N1R点处电压故障分量的变化速率就可判断该故障为区内故障还是区外故障。

由图3(a)和(b)可以看出，当MMC-HVDC直流线路发生区内正、负双极短路故障或区内正、负双极短路接地故障时，P1R点处的电压迅速下降，N1R点处电压迅速上升，所以P1R与N1R点处的电压故障分量的变化速率都非常快。由图3(c)和(d)可以看出，当MMC1侧区外发生正、负双极短路故障或MMC2侧区外正、负双极短路接地故障时，P1R与N1R点处的电压故障分量的变化速率都相对缓慢。

因此，当通过P1R处电压故障分量与N1R处电压故障分量极性判断出该故障为双极故障或者负极故障后，然后利用P1R点与N1R点处电压故障分量的变化速率快慢就可判断该故障为区内故障还是区外故障。

2 保护方法整定及保护实现流程

由前文分析可知，当系统发生故障时，P1R和N1R2个点处的电压必然发生变化，当电压变化超过门槛值时认为系统发生故障，此时可以首先通过P1R和N1R2个点处的电压故障分量的极性来判断故障发生在正极、负极或双极。

在系统发生故障的初始阶段，可以近似认为系统还是线性的，因此由叠加原理可知，故障状态可视为系统正常运行状态和故障附加状态的叠加

Ug=ΔU+U

(1)

式中Ug为故障时刻所测得的电压值,kV；U为正常运行时的电压值，kV;ΔU电压故障分量。

电压的故障分量等于故障后的测量电压值减去故障前N个周波的电压测量值，由于系统存在频率偏差，N一般取1或2.由式(1)可以得到P1R和N1R2个点处的电压故障分量UP1R和UN1R.

通过计算UP1R和UN1R的一阶差分量可以衡量其变化速率。令

(2)

式中 dUP1R和dUN1R为UP1R和UN1R的一阶差分。

当UP1R和UN1R的极性同为负时，该故障为正极故障时，如果dUP1R和远大于dUN1R，即

(3)

式中kset1为门槛值，若(3)式成立，则该故障为区内正极故障；如果dUP1R和dUN1R几乎相同，即式(3)不成立，则该故障为区外故障。

当UP1R和UN1R的极性同为正时，该故障为负极故障时，如果dUN1R远大于UP1R，即

(4)

式中kset1为门槛值，若(4)式成立，则该故障为区内负极故障；如果UN1R和UP1R几乎相同，即式(4)不成立，则该故障为区外故障。

当UP1R和dUN1R的极性不同时，该故障为双极故障时，如果P1R点处的电压故障分量的变化速率与N1R点处的电压故障分量的变化速率都很快，则只需判断dUN1R是否大于门槛值，即

dUN1R>kset2

(5)

式中kset2为门槛值，若(5)式成立，则该故障为区内双极故障，否则该故障为区外故障。

由上述分析，可以得到MMC-HVDC直流线路的保护策略，保护策略流程图如图4所示。

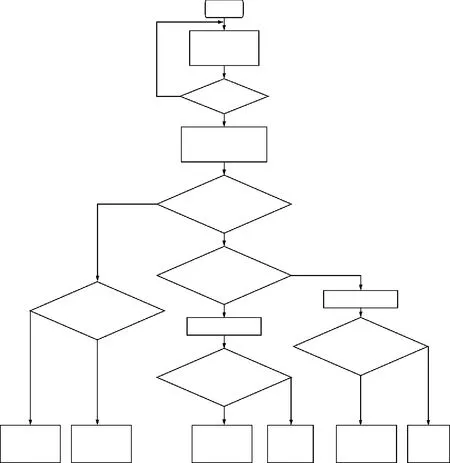
图4 保护算法流程Fig.4 Flowchart of the protection method

3 仿真验证

在PSCAD/EMTDC仿真平台上搭建了±50 kV的MMC-HVDC系统直流输电模型。该模型桥臂子模块数为10个，变压器两侧电压为10 kV/23 kV，直流侧电压为±50 kV，直流线路额定电流为0.3 kA，直流线路串联电感为0.1 H，故障均设置发生在0.8 s，故障持续时间0.1 s，数据采样频率是100 kHz，线路长度为20 km.基于该模型进行各种故障类型的仿真，用以产生故障数据，然后，利用Matlab对故障数据进行处理，进行保护算法的验证。

3.1 双极故障的故障网络单极故障仿真结果

图5(a)、(b)和(c)为发生故障1，故障5和故障6时的仿真结果。

由图5可看出：当系统正极发生故障时，P1R处电压故障分量与N1R处电压故障分量极性相同且同为负。当发生区内正极故障时，dUP1R/dUN1R的值远大于发生区外故障时dUP1R/dUN1R的值。

如图6(a)、(b)和(c)为发生故障2，故障7和故障8时的仿真结果。

由图6可以看出：当系统负极发生故障时，P1R处电压故障分量与N1R处电压故障分量极性相同且同为正。当发生区内负极故障时，dUN1R/dUP1R的值远大于发生区外故障时dUN1R/dUP1R的值。

3.2 双极故障仿真结果

如图7(a)、(b)、(c)和(d)为发生故障3，故障4，故障9和故障10时的仿真结果。

由图7可看出：当系统发生正负双极故障时，P1N处电压故障分量与N1R处电压故障分量极性不同。当发生区内故障时，dUN1R的值远大于发生区外故障时dUN1R的值。

由图5～7的仿真结果可以看出

1)当MMC-HVDC系统直流线路发生正极故障，如故障1，故障5和故障6时，P1R处电压故障分量与N1R处电压故障分量极性相同且同为负；

2)当MMC-HVDC系统直流线路发生负极故障，如故障2，故障7和故障8时，P1R处电压故障分量与N1R处电压故障分量极性相同且同为正；

3)当MMC-HVDC系统直流线路发生双极故障，如故障3，故障4，故障9和故障10时，P1R处电压故障分量与N1R处电压故障分量极性不同。

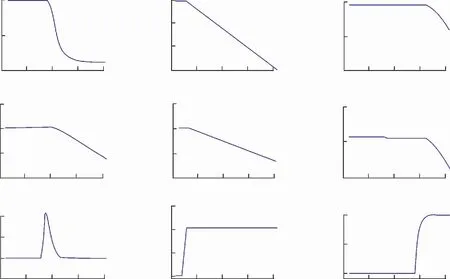
图5 正极故障仿真结果Fig.5 Simulation results of positive pole fault

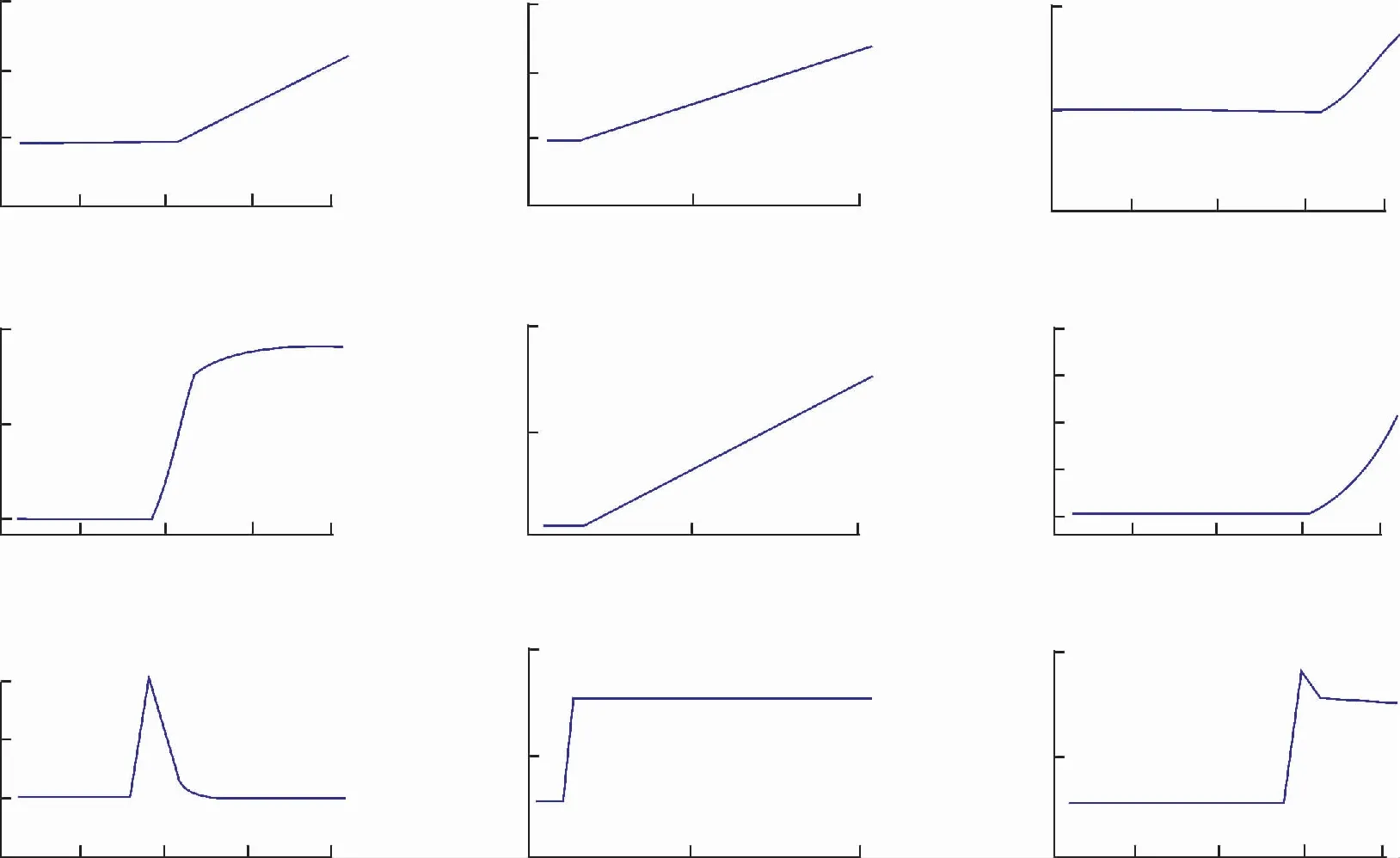
图6 负极故障仿真结果Fig.6 Simulation results of negative pole fault

因此，首先可以根据P1R处电压故障分量与N1R处电压故障分量的极性，来判别故障极。

如果系统直流线路发生正极故障，当dUP1R/dUN1R>kset1时，可以判为发生区内故障，否则为区外故障；如果系统直流线路发生负极故障，当dUN1R/dUP1R>kset1时，可以判为发生区内故障，否则为区外故障；如果系统直流线路发生双极故障，当dUN1R>kset2时，可以判为发生区内故障，否则为区外故障。