动力电池回收模式选择的多属性决策问题
2018-10-17丁雪枫
丁雪枫, 马 瑜
(上海大学 管理学院, 上海 200444)
目前,电动汽车因其具有无尾气排放、噪音小、污染小等优点,得到了世界各国政府的大力支持.但是电动汽车动力电池若不能合理回收利用,会对环境造成严重污染.2020年前后,我国电动汽车类动力电池累计报废量将达到12万~17万t,报废动力电池的回收利用需求将会越来越大[1].动力电池回收受多种因素的影响,既涉及到企业的回收能力、基础设施、回收处理技术水平等,也需要考虑回收成本、回收规模以及资源利用情况等.因此,合理回收及利用动力电池对企业而言是一项艰巨但又不可避免的问题.
目前,对于动力电池回收模式决策问题(battery recycling mode decision-making problem, BRMDP)的研究尚处于起步阶段,主要的研究成果包括:Ordonez等[2]为使电池中有价值的元素得以有效回收利用,运用定性分析法对锂电池的回收和再生技术进行研究;Turner等[3]分析比较了EPR(extended producer responsibility)和EOL(end of life)两种制度对回收率、回收效率、管理成本等的影响,并得出EPR的有效实施更有利于动力电池回收利用的结论;尤建新等[4]从环境质量成本控制角度出发考虑动力电池回收问题, 构建对称信息条件下及非对称信息条件下废弃动力电池回收商的环境质量成本控制模型和政府的环境质量检测成本控制模型,从而得出信息对称条件下更有益于动力电池回收的结论;姚海琳等[5]从动力电池回收的经济、资源与环境效益角度,设计了制造商回收、销售商回收和第三方回收3种回收模式,并采用定性方法分析比较3种回收模式.现有的研究多是从技术、制度层面,或者定性的角度对动力电池的回收模式展开的,采用定量方法研究回收模式的文章较少,可查阅到的相关文章主要是从回收成本控制的角度进行的回收问题研究.
多属性决策 (multiple attribute decision making, MADM) 问题是指在考虑多个属性的情况下,选择最优备选方案或进行方案排序的决策问题.BRMDP是在考虑多种模糊或不确定影响因素的作用下,从最优方案的选择进行决策,因此属于MADM问题.不确定语言变量(uncertain language variables,ULVs)能有效反映客观事物的复杂不确定性以及人类思维的模糊性,因此常被用于解决MADM问题.但是由于评价者评价时受到专业限制以及主观思维的影响,ULVs会有一定的局限性.Zhu等[6]基于ULVs提出了二维不确定语言变量(2-dimension uncertain linguistic variables,2DULVs)的概念.2DULVs增加了评价者对所给评价信息可靠性的描述,使得决策结果更加合理有效.Liu等[7]提出了2DULVs的运算规则、聚合算子等,并应用其解决多属性群决策问题.
VIKOR法是由Opriconvic等[8]于2004年提出的一种MADM方法.VIKOR方法可以得到最佳妥协解,能有效解决有冲突准则的决策问题,因此受到很多国内外学者的关注.You等[9]在进行供应商选择MADM问题时,提出了多准则供应商选择的区间二元语义扩展VIKOR法,通过实例验证了其方法在解决模糊信息条件下供应商选择的有效性;丁日佳等[10]在研究煤炭企业综合竞争力时,基于VIKOR法对5个煤炭企业进行实证研究,评价结果与煤炭企业综合竞争力的实际情况相符.
结合2DULVs和VIKOR的优势,本文从定性和定量的角度,提出一种基于2DULVs的VIKOR法(即2DUL-VIKOR法)求解BRMDP.从定性角度分析影响动力电池后的因素,并从定量角度进行回收模式的评价、比较与选择,这种方法有助于减少决策信息的丢失,更具有效性和稳定性,有助于更准确地做出决策.
1 背景知识
1.1 二维不确定语言变量
1.1.1不确定语言变量
设语言评价标度为:S=(s0,s1,…,sL-1),其中,sα∈S(α=0,1,…,L-1)表示语言变量,L为奇数.设si与sj任意两个语言变量,则它们具有如下性质[11-12]:
(1)若i>j,则si≻sj.
(2)存在负算子neg(si)=sL-1-i.
(3)若si≥sj,max(si,sj)=si.
(4)若si≤sj,min(si,sj)=si,si,sj∈S.
其中,性质(1)中的“≻”表示优于.L一般选取3,5,7,9等,例如:若L为5,则表示S=(s0,s1,s2,s3,s4)=(很差,较差,中,好,很好).由于在运算过程中语言决策信息可能会丢失,需要将离散语言转化成连续语言.
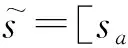
1.1.2二维不确定语言变量
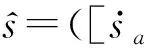
同上,为了减少评价信息的失真,一般将离散的语言评价集转化成连续集.
1.1.32DULVs运算规则
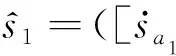
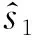
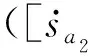
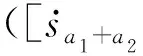
(1)
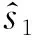
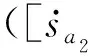

(2)
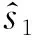
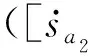
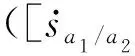
(3)
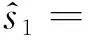
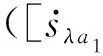
(4)
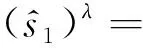

(5)
1.1.4Hamming距离
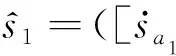
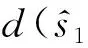
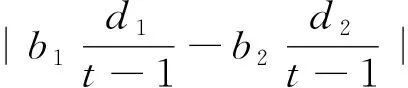
(6)
1.1.5期望值
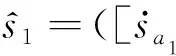
(7)

1.2 聚合算子
1.2.1GWA(geometric weighted aggregation)算子

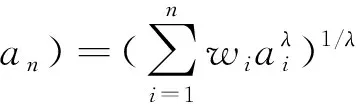
(8)
则GWA函数称为广义加权平均算子,简称GWA算子.
1.2.2PA(power average)算子
定义6[14]设(a1,a2,…,an)为实数集合,若满足
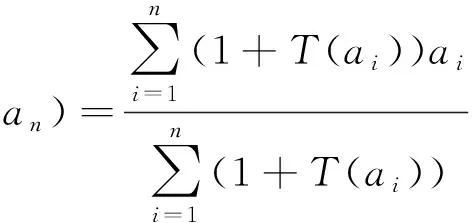
(9)
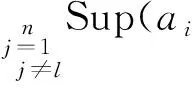
1.2.32DULPGWA算子
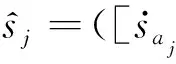

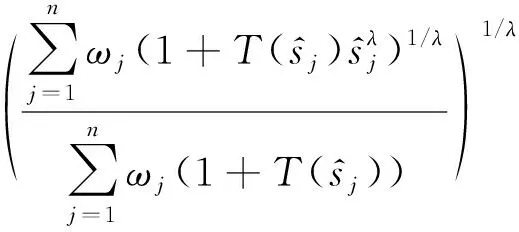
(10)
其中,λ变量的取值范围为(0,+∞),则称2DULPGWA为二维不确定语言变量广义加权集结算子,简称2DULPGWA算子.
由公式(1)~(5),可得
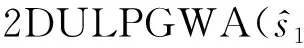
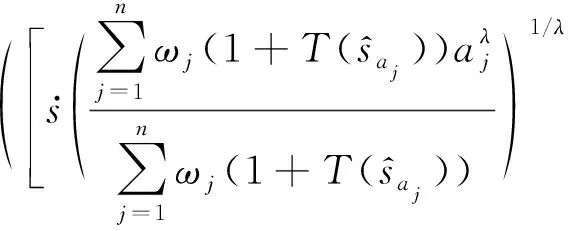
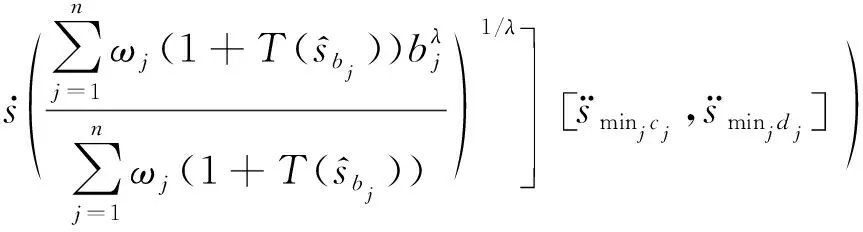
(11)
1.3 VIKOR法
VIKOR方法通过确定正理想解和负理想解,对各个评价对象的指标值与理想解的接近程度进行判断.其中,正理想解是各评价指标中的最佳值,而负理想解是各评价指标中的最差值.VIKOR方法综合考虑群体和个体的妥协关系,可从几组备选方案中确定折衷方案.假设A=(A1,A2,…,Am)为m个方案的集合,C=(C1,C2,…,Cn)是n个指标集合,方案Ai在考虑指标Cj影响下的评价值为rij,构成决策矩阵R=(rij)m×n,则VIKOR计算步骤如下[8]:
Step 1 将决策化信息集R=(rij)m×n转化为规范化信息集D=(sij)m×n.
(12)
式中:I1和I2分别表示效益型和成本型的下标集;N={1,2,3,…,n}.
Step 2 确定各个评价对象的理想解与负理想解为
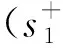
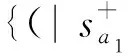
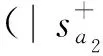

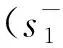



(13)
Step 3 计算各评价对象的群体效用值、个别遗憾值分别为
(14)
(15)
Step 4 计算综合排序指标Qi.
(16)
当满足以下条件时,Qi排序中值最小的方案被认为是最优的方案.
条件1利益被接受的条件满足
Q(a2)-Q(a1)≥1/(I-1)
式中:a1表示根据Qi排序得到的第一个备选方案;a2表示根据Qi排序得到的第二个备选方案;I为备选方案的数目.
条件2决策可靠性被接受的条件:对Qi值按照从小到大进行排序,排在前两位的结果满足排在第一位的备选方案的群体效用值Si必须同时比排在第二位的备选方案的群体效用值小;或者根据R值排序结果,排在第一位的备选方案的个别遗憾值必须同时比排在第二位的备选方案的个别遗憾值小.
方案评判准则:如果不满足条件1和条件2中的任何一个,那么会得到一个折衷解集.
2 2DUL-VIKOR决策模型
2.1 问题描述

2.2 决策过程
这里,采用2DUL-VIKOR方法对所有备选方案进行决策,决策过程如图1所示.
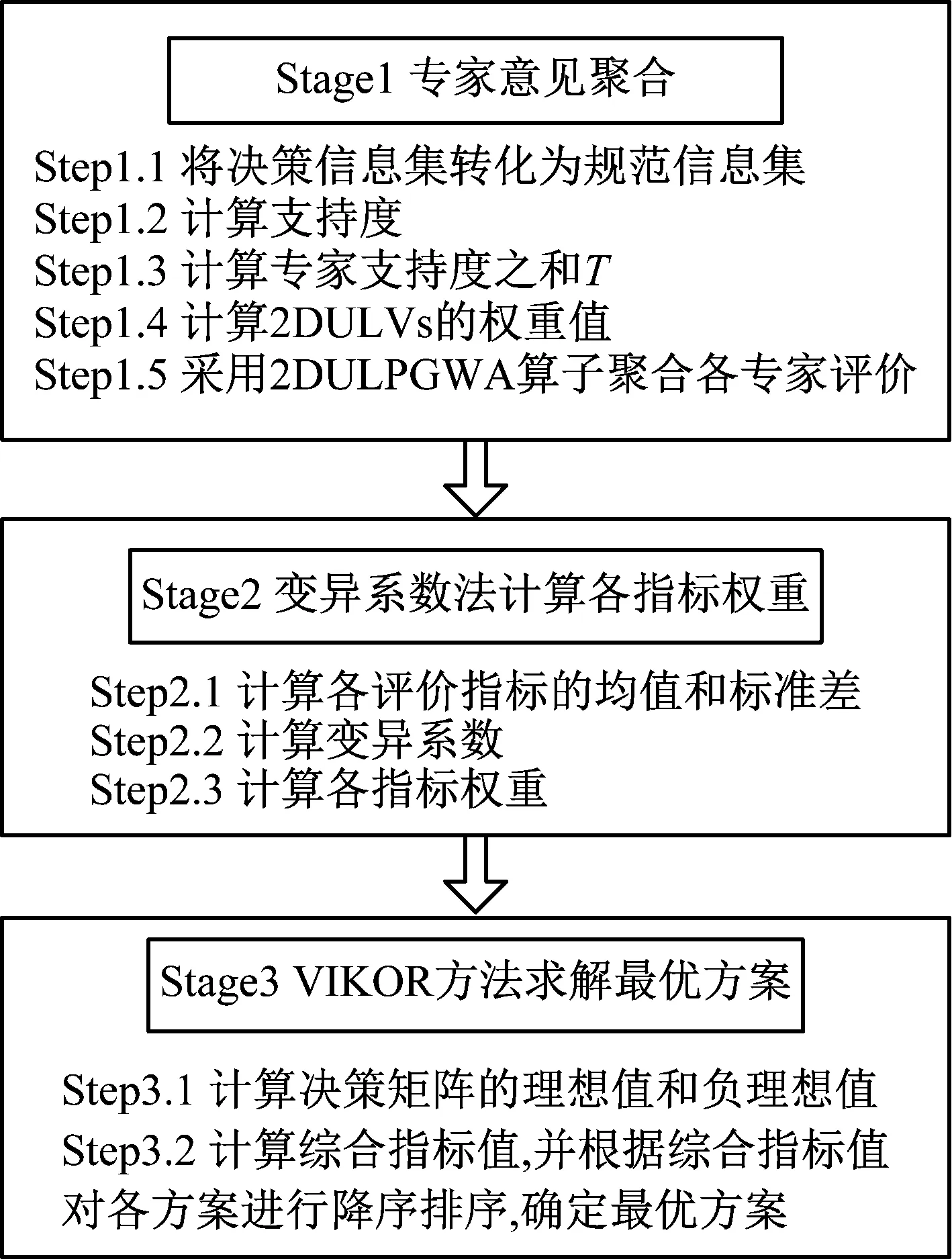
图1 2DUL-VIKOR方法基本流程图
2DUL-VIKOR方法的具体决策步骤如下:
Stage 1 专家意见聚合.
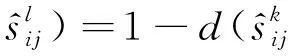
(17)
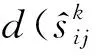
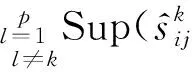
(18)
(19)
Step 1.5 采用2DULPGWA算子聚合专家的评价信息.
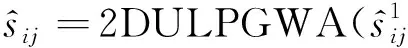
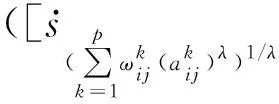
(20)
Stage 2 变异系数法计算指标权重.
变异系数法是一种客观赋权方法,它是利用各项评价指标所包含的决策信息,并根据观测值的变异程度大小,来确定指标权重[15].此方法直接根据指标实测值经过一定数学处理后获得权重信息,使用各个构成要素内部指标权重的确定,因此指标的信息价值可以得到充分体现,观测值变异系数的大小可以较好地区分各个方案在评价指标的重要程度.观测值变异系数越大则赋予其权重值就越大;反之,权重值越小.假设指标值rij是规范化的评价值.
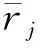
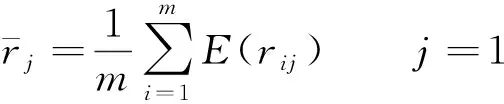
(21)

(22)
Step 2.2 计算变异系数Yj.
,2,…,n
(23)
Step 2.3 计算指标权重wj.
,2,…,n
(24)
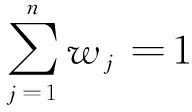
Stage 3 求解最优方案.
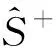

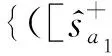
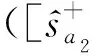
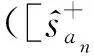


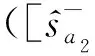
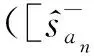
(25)
Step 3.2 根据公式(14)~(16),计算综合指标值Qi,并进行降序排序,确定最优解.
3 算例
3.1 案例描述

3.2 方案评价
采用所提出的2DUL-VIKOR方法对A企业电动汽车动力电池的回收模式进行决策.
Stage 1 专家意见聚合.

表1 专家e1对方案Ai在指标Cj影响下的2DUL评价矩阵

表2 专家e1针对3个备选方案的规范化评价值
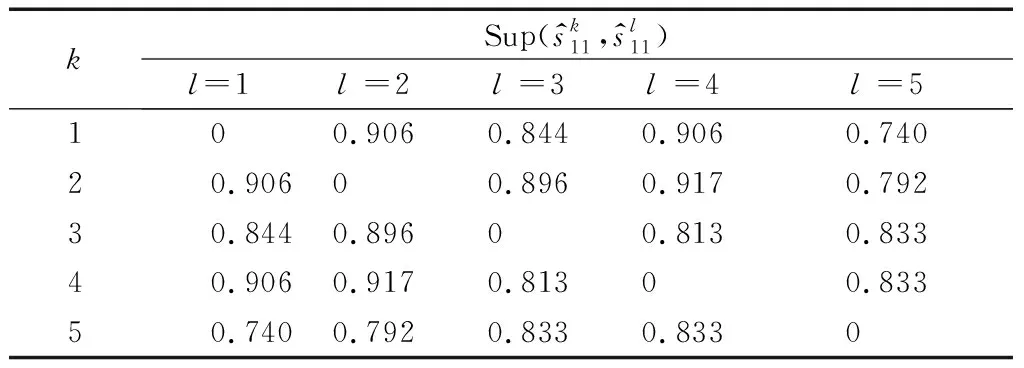
表3 专家e1的支持度值
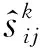

Step 1.5 根据公式(20)采用2DULPGWA算子对各专家评价进行聚合,结果如表4所示.

表4 2DUL聚合决策矩阵
Stage 2 采用变异系数法计算指标权重.
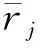
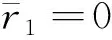
D1=0.194,D2=0.139,D3=0.121,D4=0.115,D5=0.122,D6=0.230.
Step 2.2 采用公式(23)计算第j项指标的变异系数Yj.
Y1=0.443,Y2=0.316,Y3=0.274,Y4=0.429,Y5=0.493,Y6=0.512.
Step 2.3 采用公式(24)计算指标权重wj.
w1=0.180,w2=0.128,w3=0.111,w4=0.174,w5=0.200,w6=0.207.
Stage 3 求解最优方案.
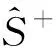
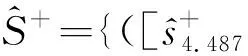

Step 3.2 根据公式(14)~(16),计算综合指标值Qi,并根据Qi值进行降序排序,确定最优解.
S1=1.058,S2=0.903,S3=1.050;R1=0.267,R2=0.215,R3=0.231;Q1=1,Q2=0,Q3=0.627,其排序结果为:Q2Q3Q1.Qi同时满足2.3节中Step4的条件1和条件2,故备选方案的排序为:A2≻A3≻A1.A2为最佳方案.
综上所述,A企业选择A2,即生产商联盟对动力电池进行回收最为合适.A2回收模式的优势主要体现在:①回收设施以及专业性较生产商自主回收更强;②生产商联盟回收可分担逆向物流回收成本;③动力电池回收后资源的利用率较第三方回收模式更高.
4 结语
本文从电动汽车生产商的角度针对动力电池回收模式的多属性群决策问题进行研究,通过文献回顾分析了2DULVs以及VIKOR法各自求解多属性决策问题的优势及局限,提出了一种基于2DULVs与VIKOR相结合的2DUL-VIKOR法.首先,在进行专家意见聚合时运用2DULPGWA算子,确保聚合信息的准确性;其次,运用变异系数法求解指标权重,保证其客观性;结合VIKOR法求解聚合后的信息集并进行排序,求得最优解;最后结合实例对所提出的方法的有效性和实用性进行验证.现阶段,综合考虑经济效益、回收成本以及资源利用方面的影响,动力电池的回收采取生产商联盟模式较为适合.
