基于层次分析法的物流配送车辆选型研究

索明亮 （中国国际工程咨询有限公司，北京 100048）

0 引言

物流配送是现在物流行业实现资源最优配置的重要经济活动，物流配送车辆选型是依据供应方、配送中心以及需求方进行合理选择车辆规格的研究，因此需要科学的定量和定性分析。车辆执行配送任务，要求以合理的资源，并在最短的时间，将商品从供应方向需求方实现转移，避免车辆资源的浪费，从而制定最优的车辆配送方案。

由于影响物流配送车辆选型的因素较多，目前还没有可靠的定性、定量评价方法。本文采用层次分析法（AHP），将较为复杂、模糊的问题做出决策，通过计算各影响因素的权重值，进而确定车辆规格选型。

1 物流配送车辆选型的目标

制定物流配送车辆选型的目标需要考虑企业、客户和社会的利益[1]：（1）客户对配送时间、安全性要求较高；（2）企业为了提高效益，通过选择适宜配送车辆、最优路径来实现共同和多点配送，以降低企业成本，增加企业收入；（3）社会利益主要考虑到减少车辆造成的道路拥挤和废弃排放等。

本文确定物流配送车辆选型目标的最优化，是在商品供应方所提供既有配送车辆的基础上，综合考虑影响车辆选型目标的各个因素，通过计算各影响因素的权值，并借助于一致性检验，最终选择最优载重的车辆，以期望达到用户对物流配送的基本要求、企业对效益最高化的追求以及社会良好利益的体现。

2 物流配送车辆选型的影响因素

物流配送是一个较为复杂的过程，涉及到多方面的利益，因此在确定合理的车辆选型目标之前，需要对各影响因素进行分析。

2.1 商品供应及需求能力。在物流配送车辆选型过程中，商品的供应及需求能力是重要的一个影响因素。商品供应不足，不仅无法满足客户对商品的需求期望，而且还会直接影响到配送车辆的选择。配送车辆选择不合理，会导致资源浪费，无法达到企业资源的优化配置，减低企业成本；情况严重的，甚至有损企业在客户中树立的良好业务形象。

2.2 交通拥挤与安全。交通拥挤和安全对配送车辆选型的影响也是显著的。主要表现为：道路拥挤严重影响配送车辆的快捷和准时性，车辆行驶缓慢不仅增加油耗，而且增加企业配送成本[2]；道路交通安全程度关系到配送货物是否能准时安全的到达，以及配送公司的经济效益，因此影响着配送车辆的选择，对车辆的性能、安全性等要求较高，且车辆应尽量避免途经事故高发路段或交叉口。

2.3 交通组织。交通组织主要是指交叉口的转向限制（禁左、禁右）以及路段对车辆的限制（车辆类型、最大高度、最大长度等）[2]。在物流配送过程中，配送车辆类型多样，共同配送或不同商品的配送需要用到不同类型的车辆，同时还会受到道路条件和道路组织的约束。因此，交通组织会影响配送车辆的选择，要求在既有道路条件和道路组织的条件下，合理选择配送车辆，完成配送任务。

3 层次分析法模型

层次分析法（Analytical Hierchy Process，AHP）是针对系统特征，应用网络系统理论和多目标综合评价方法而发展起来的。层次分析法提出了递阶层次结构理论，根据问题的性质和要达到的总目标将问题分解为不同的组成因素，并按照因素间的相互关联影响以及隶属度关系将其按不同层次聚集组合，从而形成一个多层次的分析结构模型，然后对这种递阶层次结构进行定量化描述，从而考察系统的结构和功能，最后通过排序理论得出满足总目标要求的各个方案优劣次序。

层次分析法的具体步骤如下：

3.1 建立评价对象的树状层次结构模型。建立层次分析结构是层次分析法中最重要的一步，为此就要对系统进行深入分析，弄清系统的范围、所包含的因素、因素之间的相互关系和最终需要解决的问题[3]。配送车辆选型的过程中涉及的因素比较多，选择时首先要考虑各因素的重要性、影响力或者有限程度，其次选择具有较大差异的因素，忽略方案中条件基本相同的因素，建立准则层和指标层。

3.2 构造各层判断矩阵。确立判断定量化的标度，通过对各因素进行两两比较，构造判断矩阵A：

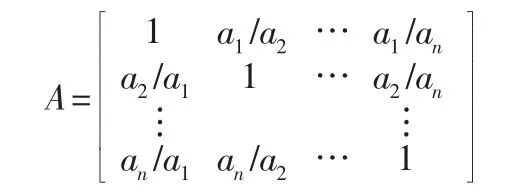
式中：aii为物体的n个部分中的第i部分的地位（分量、作用、重要性）；而ai/aj为第i部分相对于整体而言比第j部分重要的倍数。通过求解方程得到表示整体的向量B。当方程满足一致性，则矩阵A的最大特征量λmax=n，此时λmax对应的特征向量为B。矩阵A按照表1的标度原则得出，如表1所示。

表1 判断矩阵标度含义

3.3 层次单排序及其一致性检验。层次单排序是指根据判断矩阵对于上一层某一因素而言，本层次与之有关系的因素的重要性次序的权值，即计算判断矩阵的最大特征值及对应的特征向量，并将特征向量归一化后就得到各因素的相对权重[4]。

层次单排序一致性指标为：

其中，CI（n）=（λmax-n）/（n-1 ），n为参与对比的因素个数；RI（n）的值在平均一致性指标表中查取，如表2所示。

表2 平均随即一致性指标表

当判断矩阵A的随即一致性比率CR（n）＜0.1时，认为判断矩阵A具有满意的一致性，否则就需要调整判断矩阵，使之具有满意的一致性。

3.4 层次总排序，得出决策结果。利用层次单排序的计算结果，进一步计算出层次分析模型中方案层中所有要素相对于目标层的组合权重。根据权重的大小即可得到各方案的优劣，从而为选择最优方案，使整个系统达到最优化提供依据。

4 实例分析

本文基于层次分析法的物流配送车辆选型的研究，是在企业既定车型的基础上，以选择最合理的配送车辆为目标，全面考虑各个影响因素，通过计算各影响因素的权重值，并借助于一致性检验，最终选择最优配送车辆，以期望满足企业、客户以及社会利益。

某企业进行物流配送任务，可供选择的配送车辆类型有：（1）载重0.8T的车辆；（2）载重1.5T的车辆；（3） 载重2.0T的车辆。本文采用层次分析法来确定最优配送车辆类型，建立技术流程图，如图1所示。

4.1 建立层次结构。根据技术流程图，构建物流配送车辆选型树状层次结构图，如图2所示。

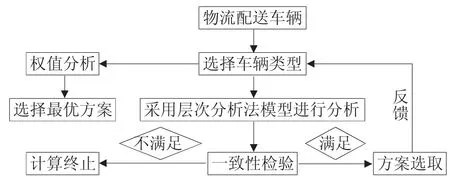
图1 物流配送车辆选型技术流程图

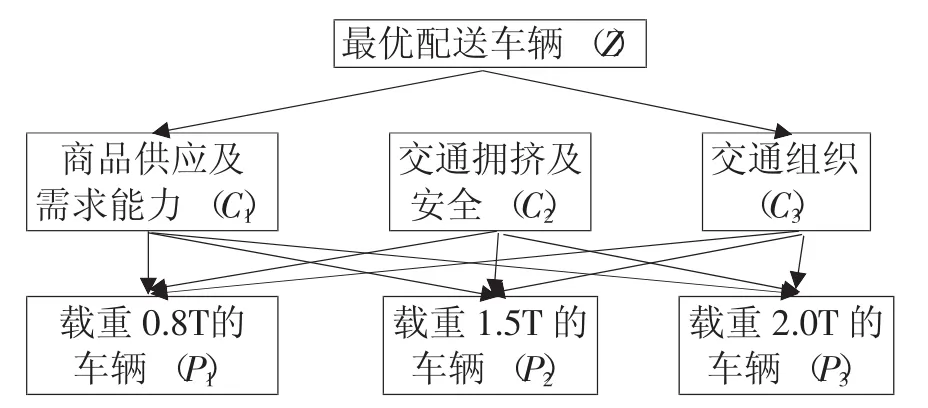
图2 物流配送车辆选型树状层次结构图

第一层为目标层（Z），第二层为准则层（C ），第三层为方案层（P）。

4.2 构造判断矩阵并进行一致性检验。当矩阵C=（cij）n*n满足如下条件时：

则称C为互反矩阵。

通过以上对多个影响因素的分析，参照物流配送车辆选型层次结构图，广泛征集项目专家组意见，并根据项目专家组评分，建立判断矩阵，进而进行加权计算。

（1） 建立判断矩阵Z-C，如表3所示。

表3 Z-C判断矩阵

（2） 建立判断矩阵C1-P，C2-P和C3-P。

计算公式如下：

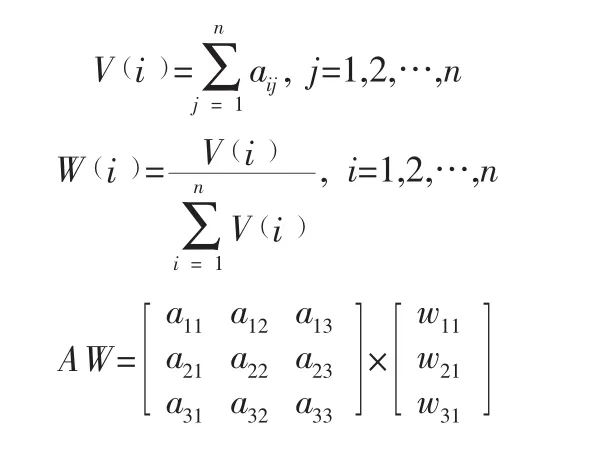
经计算，如表4、表5和表6所示。

表4 C1-P判断矩阵

表5 C2-P判断矩阵

表6 C3-P判断矩阵

（3）求解λmax，并进行CR（n）平均随即一致性比率检验。

①对于C1-P判断矩阵有，λmax=Σ［ AW（i）/W（i）］/n（n为阶数，本文中n=3）。

经计算，λmax=3，所以CI（n）=（λmax-n）/（n-1），即CI（n）=0，此时n=3。

又因CR（n）=CI（n）/RI（n），当n=3时，查表RI（3）=0.58，所以：CR（3）=CI（3）/RI（3）=0/0.58=0＜0.1，则判断矩阵具有满意的一致性。

②对于C2-P 和C3-P，两者与C1-P 具有相同的特征根，CR（3 ）=0＜0.1，判断矩阵也具有满意的一致性。

经检验，均满足要求。

4.3 层次总排序，选取最优方案。利用以上计算结果，进一步得出层次分析模型中方案层相对于目标层的组合权重。根据计算所得总排序权重值的大小进行方案比选，从而选择最优方案，计算结果如表7所示。

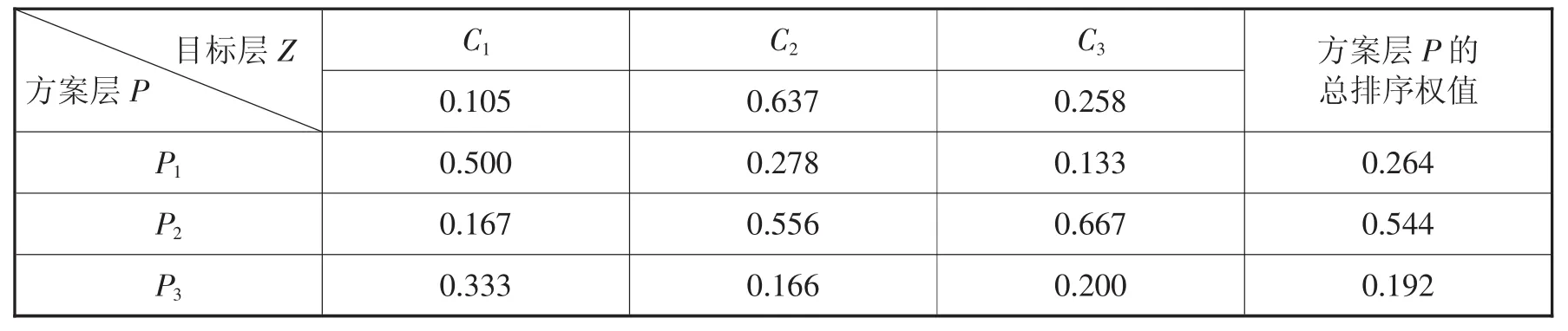
表7 层次总排序权值

由表7可知，方案层P的总排序权值为P1=0.264，P2=0.544，P3=0.192。所以方案P2优于P1，P1优于P3，故方案P2为最优方案，即企业进行物流配送应选择载重1.5T的车辆。

5 结论

本文采用层次分析法进行物流配送过程中车辆选型的研究，充分利用了该方法在处理多准则、复杂问题方面的优点。通过实例分析，表明该方法在一定程度上具有较好的适用性，能够有效地解决问题。同时，在采用层次分析法确定权重时，需广泛征集有关人员和专家意见，使计算所得权重更好地符合实际情况，最大限度提高层次分析法模型的适用性。