基于BP神经网络的土壤侵蚀预测模型对比

孙 毅

(太原理工大学水利科学与工程学院，山西太原030024)

1 研究背景

土地是维系人类繁衍生息的基本资源。水土流失现象危害极严重，首先会直接导致可耕作土地资源的减少［1］，其次流失的土壤会引起河道的淤积问题［2］，此外水土流失也是土壤养分流失的重要诱因［3］。因此，开展水土流失机制、防治和预报等方面的工作，对环境保护、农业增产和促进经济社会的可持续性发展具有极其重要的作用和意义。

目前，诸多学者从水土流失机制和预测2个方面开展了较多的科学研究，并取得了一定的成果。在水土流失机制方面，主要开展了降水［4－5］、坡度和坡型［6－7］、植被类型和植被覆盖度［8－9］、土壤类型［10－11］、耕作措施［12－13］对土壤侵蚀量的影响研究，结果表明，这几项因素对侵蚀量的影响均较为显著。在土壤侵蚀预测方面，主要构建了一系列的经验模型［14－16］和物理模型［17－18］，随着人工智能算法的发展，反向传播(back propagation，简称BP)神经网络在土壤侵蚀预测方面得到了广泛的应用［19－23］。但前人建立的模型输入项常常忽略了一些重要因素，主要包括植被覆盖程度［20］、土质因素［21－22］、降水［23］等。此外，前人所建立的模型还存在适用范围小、所采用的传统算法存在搜索空间大，易陷入局部极值点等问题，这几点限制了前人建立的模型在实际预测中的广泛应用。因此，对全国较大范围内土壤侵蚀量预测的研究有待进一步深入，模型优化算法的改进也是十分必要的。

万有引力搜索算法(gravitational search algorithm，简称GSA)和人群搜索算法(seeker optimization algorithm，简称SOA)具有较好的收敛速度和寻优精度。目前，基于万有引力算法和人群搜索算法优化后的BP神经网络模型在水土流失方面的预测还未见相关报道，同时哪种模型更适合土壤侵蚀预测研究同样也有待进一步深入。因此，本研究旨在构建基于万有引力算法和人群搜索算法优化的BP神经网络模型，实现土壤侵蚀的准确预报，以期为水土流失预测工作提供支持。

2 BP神经网络模型原理

BP神经网络是目前应用最广泛的神经网络模型之一。图1为BP神经网络的工作原理和基本网络结构，它主要由输入层、隐含层和输出层3部分构成，m、q、n分别为这3层神经元的节点数，三者的职责各不相同，输入层负责接收外界的输入信息、隐含层负责内部信息的变换处理、输出层负责向外界传输处理结果。完成1次完整的正向传播处理后，若输出信息与期望不吻合，便进入误差反向传播机制，通过不断调整各层之间的网络权值和阈值，使神经网络的误差平方和最小，如此反复直至达到期望要求为止。

3 优化算法流程

3.1 万有引力算法流程

万有引力算法将所有粒子当作有质量的物体，在寻优过程中，所有粒子做无阻力运动。每个粒子都会受到空间中其他粒子万有引力的影响，并产生加速度，向质量更大的粒子运动。由于粒子的质量与粒子的适度值相关，适度值大的粒子其质量也会更大。因此，质量小的粒子在朝质量大的粒子趋近的过程中逐渐逼近最优解。GSA的具体流程为

(1)设置初始化算法中所有粒子的位置与加速度，并设置迭代次数与算法中的参数。

(2)对每个粒子计算该粒子的适应值，利用公式(1)更新重力常数。

式中:G(t)表示随引力变换的万有引力常数;G0表示在t0时刻的G取值;T表示最大迭代次数;t表示时间;a表示粒子的加速度。

(3)由计算得到的适应度，利用公式(2)和公式(3)计算每个粒子的质量。

式中:fiti(t)表示粒子i的适应值;best(t)表示t时刻的最优解;worst(t)表示t时刻的最差解;mi(t)、mj(t)表示将第 i、j个粒子的适应值分别规范化到［0，1］之间;Mi(t)为粒子i的质量;N为粒子数。

(4)利用公式(4)至公式(7)计算每个粒子的加速度。

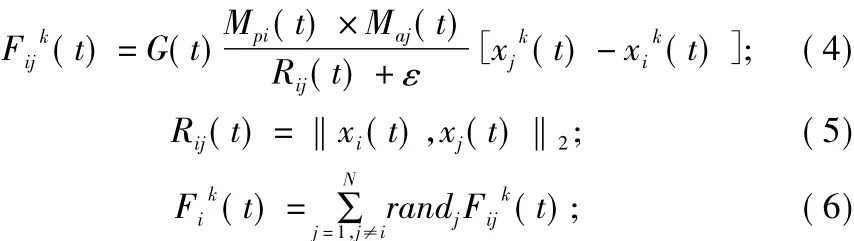
式中:ε表示1个非常小的常量;Maj(t)表示作用粒子j的惯性质量;Rij(t)表示粒子xi和xj的欧氏距离;(t)表示在第t次迭代过程中粒子i受到的作用力;(t)表示在第t次迭代过程中，个体j作用于个体i的力;Mii(t)表示被粒子的惯性质量;Mpi(t)表示作用粒子i的惯性质量;(t)、(t)为第j个和第i个粒子在第k维空间的位置;xi(t)和xj(t)为t时刻第i个和第j个粒子的位置;randj表示［0，1］区间的伪随机数;t)表示粒子i在第k维空间t时刻的加速度。

(5)根据公式(8)计算每个粒子的速度，然后更新粒子的位置。

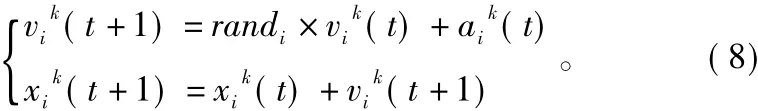
(6)如果未满足终止条件，返回步骤(2);否则，输出此次算法的最优解。

3.2 人群搜索算法流程

SOA模拟人的智能搜索行为，立足传统的直接搜索算法，以搜索队伍为种群，搜寻者位置为候选解，通过模拟人类搜寻“经验梯度”和不确定推理，完成对问题测定的最优求解。SOA的实现步骤及具体过程如下:

(1)t→0。

(2)初始化。在可行解域随机产生s个初始位置:

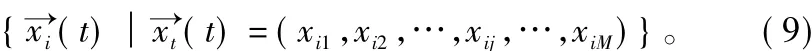
其中，i=1，2，3，…，s;t=0;M 为搜索空间中维数 j的最大值。

(3)评价。计算每个位置的目标函数值。

(4)搜寻策略。计算每个个体i在每一维j的搜索方向dij(t)及步长αij(t)。

(5)位置更新。按公式(9)更新每个搜寻位置。

(6)t→t+1。

(7)若满足停止条件，停止搜索;否则，转至步骤(3)。

其中，每一步分别计算每个搜寻者i在每一维j的搜索方向 dij(t)和步长 αij(t)，且 αij(t)≥0，dij(t)∈{ －1，0，1)(i=1，2，3，…，s;j=1，2，3，…，M)。dij(t)=1 表示搜寻者 i沿着 j维坐标的正方向前进;dij(t)=－1表示搜寻者i沿着j维坐标的负方向前进;dij(t)=0表示搜寻者i沿着j维坐标保持静止。确定搜索方向和步长后，根据公式(10)和公式(11)，进行位置更新，通过不断更新搜寻者的位置，得到更好的搜寻者，直到得到满意的结果。

4 神经网络模型的构建

4.1 神经网络输入层、输出层的确定

本研究中的数据来源于《中国水土保持公报》［24］，样本为全国不同水土流失典型监测点的土壤侵蚀量资料。围绕影响土壤侵蚀量的诸多因素，从中筛选出物理意义表达明确和影响程度较高的5项作为该模型的输入项，分别为地形、坡度、土壤类型、植被措施和降水。该模型的输出项为土壤侵蚀量，总样本数为194个，以7∶3的比例将该样本分为训练集和预测集，即样本数分别为136个和58个。

4.2 神经网络结构的确定

当隐含层数量增加时，一定程度上会提高模型精度，但也可能会造成模型过于复杂等问题，通常选择单隐含层为宜。隐含层节点数量一般通过经验法与试算法相结合进行确定。根据经验公式(12)可知，最优节点数范围为4～12。输入层和隐含层、隐含层和输出层之间的信息传递分别采用logistic函数和purlin函数进行传递，神经网络的训练函数为trainlm，训练目标误差为0.000 1，最大训练次数为5 000次。

式中:m为输入层节点数;q为隐含层节点数;n为输出层节点数;a为1到10之间的整数。

5 结果与分析

5.1 最优隐含层节点数的确定

由图2可知，当隐含层节点数增加时，神经网络模型模拟值与实测值的平均相对误差(mean absolute percentage error，简称MAPE)和均方根误差(root mean square，简称RMSE)均呈现先逐渐减小后逐渐增大的变化趋势。在多次试算中，当隐含层节点数为7个时，经过2 384次训练后，模型的训练误差为7.108 9×10－5，能够达到模型的训练精度要求。因此，认为7个为合理的节点数。综上所述，本研究中模型的拓扑结构为5－7－1。

5.2 训练组模拟效果评价

图3为训练样本的训练效果图。由图3－a可知，BP、GSA－BP和SOA－BP模型的预测值与实测值间的线性方程的斜率分别为 0.988 3、0.998 3、1.010 0，说明所建立的 3 种模型的预测值和实测值间均具有较好的一致性。由图3－b可知，BP、GSA－BP、SOA－BP模型的绝对百分误差分别介于0.11% ～11.83%、0.07% ～9.85%和 0.10% ～6.70% 之间，平均相对误差分别为6.73%、4.44%和 3.18%，3种模型的训练误差大小表现为BP＞GSA－BP＞SOA－BP。此外，采用t检验统计学方法对3种模型的预测值和实测值间的差异性进行分析。由表1可知，3种模型的预测值与实测值之间均无统计学差异。综上所述，3种模型均满足较好一致性、较高模拟精度的条件，达到了训练要求，均可以用来进行土壤侵蚀量的预测工作。总体而言，SOA－BP模型的训练效果最优。

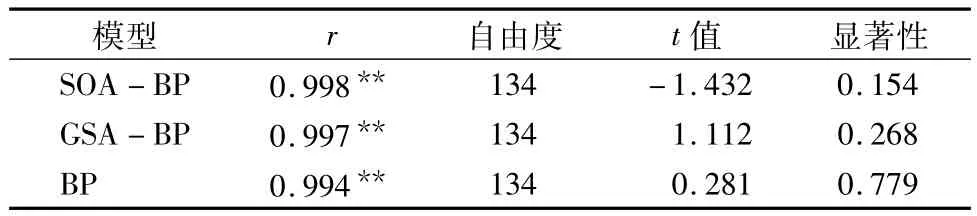
表1 实测值与预测值t配对检验结果(训练组)

5.3 预测组模拟效果评价

由图4－a可以看出，BP、GSA－BP、SOA－BP模型的预测值与实测值间线性方程的斜率分别为0.988 3、0.989 0和0.999 5，说明建立的3种模型的预测值和实测值间均具有较好的一致性。由图4－b可知，BP、GSA－BP、SOA－BP模型的绝对百分误差分别介于 0.35% ～13.89%、0.43% ～9.88%、0.01% ～6.81%之间，平均相对误差分别为7.60%、5.63%、3.62%，说明 SOA－BP模型的预测误差最小。此外，采用t检验统计学方法对3种模型预测值和实测值间的差异性进行分析。由表2可知，3种模型的预测值与实测值间的差异性均未达到显著水平。综上所述，3种模型的预测值与实测值之间具有较好的一致性和较高的模拟精度，为土壤侵蚀预测提供了一种高效准确的定量研究方法。相对而言，3种模型的预测效果好坏表现为SOA－BP＞GSA－BP＞BP。

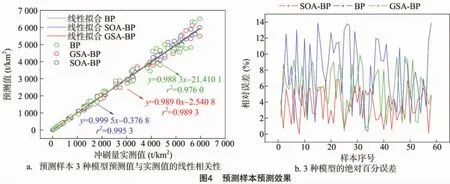
表2 实测值与预测值t配对检验结果(预测组)

6 结论

本研究以我国水土流失典型监测点土壤侵蚀模数为样本，建立了基于BP神经网络的土壤侵蚀预测模型，并分别采用万有引力搜索算法和人群搜索算法对权值和阈值进行优化，从而得到GSA－BP、SOA－BP预测模型，并对3种模型的性能好坏进行对比研究。主要结论为(1)GSA－BP和SOABP模型分别融合了2种算法的局部搜索、全局迭代能力和神经网络的泛化能力，可以实现全国水土流失典型监测点土壤侵蚀量的准确预报。(2)BP、GSA－BP、SOA－BP模型训练样本的平均相对误差分别为6.73%、4.44%、3.18%，3种模型的训练样本误差大小表现为BP＞GSA－BP＞SOA－BP。(3)BP、GSA－BP、SOA－BP模型预测样本的平均相对误差分别为7.60%、5.63%、3.62%，3种模型的预测误差大小表现为BP＞GSA－BP＞SOA－BP。