具有脉冲效应的2个食饵1个捕食者系统的稳定性

刘 娟，赵 清，程彩萍，张海峰

(1.山西农业大学文理学院，山西太谷030801;2.山西农业大学农学院，山西太谷030801)

众所周知，害虫会对农作物及人类造成很大的危害，因此研究害虫治理方法是非常必要的。利用化学防治的快速性和生物防治的无污染性，提出比任一单一控制更优的害虫综合治理策略，此课题引起国内外学者的广泛关注［1－10］，其中数学学者引入脉冲微分方程来描述此不连续的瞬时行为［1－10］。国内外学者对1个食饵1个捕食者系统进行了大量的研究［1－4］，但是实际中天敌不仅仅只捕食1类害虫，而且害虫的种类也不只1种［6－8］。例如蚜虫和梨木虱都取食梨树汁液，都为梨树的害虫，瓢虫同时捕食蚜虫和梨木虱，为它们共同的天敌。Zhang等研究了2个食饵1个捕食者系统，但是仅讨论了在同一固定时刻投放天敌和喷洒农药的模型［6］。基于上述事实，本研究利用具有Holling II和Monod－Haldance功能性反应的脉冲微分方程，建立在不同脉冲时刻分别投放天敌和化学农药的2个食饵1个捕食者模型，并研究此模型的动力学行为。

1 模型的建立

本研究假设在没有捕食者时，2类食饵均呈Logistic增长趋势，捕食者对食饵分别具有HollingⅡ和Monod－Haldance功能性反应，建立如下模型:

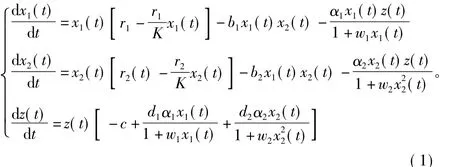
式中:x1(t)、x2(t)、z(t)分别表示t时刻2类食饵、捕食者的数量;c表示捕食者的死亡率;r1、r2分别为2类食饵的增长率;b1、b2分别为2类食饵种群间的竞争系数，b1＞0，b2＞0;d1、d2分别为捕食者对2类食饵的消化率;K为环境容纳量;别为 HollingⅡ、Monod－Haldance功能性反应函数，其中 α1、w1、α2、w2都为正常数。

当2个食饵灭绝，即x1(t)=0、x2(t)=0时，模型(1)有一个不稳定的平衡态(0，0，0)，但此时捕食者也趋于灭绝，系统没有无害虫平衡点，因此用连续模型(1)无法对害虫进行很好的控制。

考虑到化学农药对天敌的影响，本研究建立在不同固定时刻分别投放捕食者和喷洒化学农药的脉冲动力系统:

式中:Δxi(t)=xi(t+) － xi(t)(i=1，2)，Δz(t)=z(t+) －z(t);T为脉冲周期;μ为t=nT时投放捕食者的数量，μ＞0;p1、p2、p3分别为t=(n+l－1)T时因喷洒化学农药杀死的食饵、捕食者的比例，其中n为正整数，l为(0，1)的任意实数，p1、p2、p3取值范围为［0，1)。

引理1 模型(2)的解［x1(t)，x2(t)，z(t)］是连续可微的，且前3个方程右端函数的光滑性保证了解存在唯一性。

引理2 设X(t)=［x1(t)，x2(t)，z(t)］为模型(2)的解，且初始条件X(0+)≥0，则对于所有的t≥0有X(t)≥0。若初始条件X(0+)＞0，则对于所有的t≥0有X(t)＞0。

考虑模型(2)中x1(t)=0、x2(t)=0时的状况，得出如下脉冲微分方程:

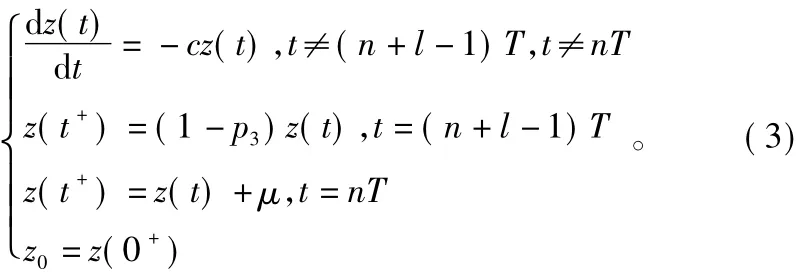
由频闪映射和不动点定理可知，模型(3)有如下周期解:

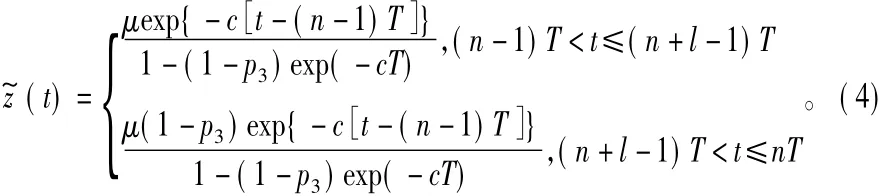
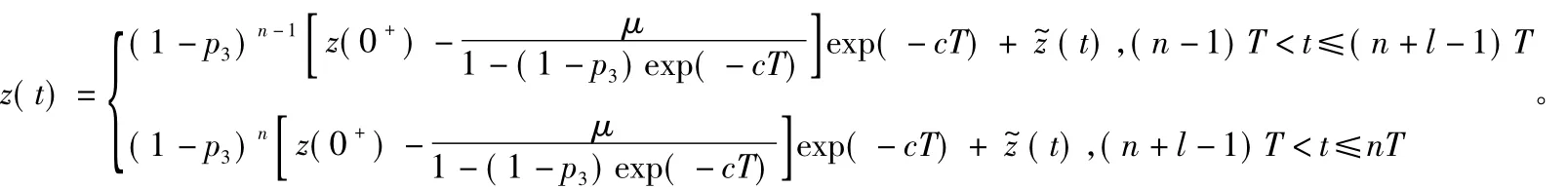
引理 模型(2)的任意正解z(t)在t→∞时有z(t)→z～(t)。

因此模型(2)有1个食饵全部灭绝周期解，为［0，0，z～(t)］。

2 食饵全部灭绝周期解的渐近稳定性

定理1 设［x1(t)，x2(t)，z(t)］为模型(2)的任意解，如果满足 T≤min{T1，T2}，则 2类食饵全部灭绝周期解［0，0，z～(t)］是局部渐近稳定的。其中T1，T2分别为f1(T)=0、f2(T)=0的根。

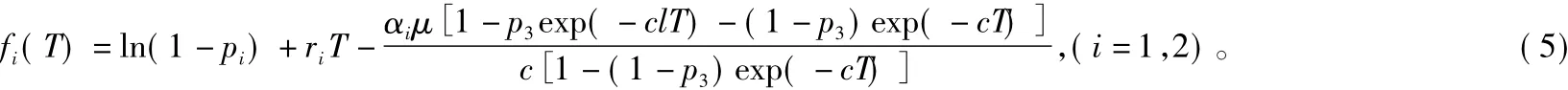
证明:定义 u(t)=x1(t)，v(t)=x2(t)，w(t)=z(t) －z～(t)，代入模型(2)中，通过Taylor展开式并取其线性部分得:

设φ(t)为模型(6)的基解矩阵，则满足:

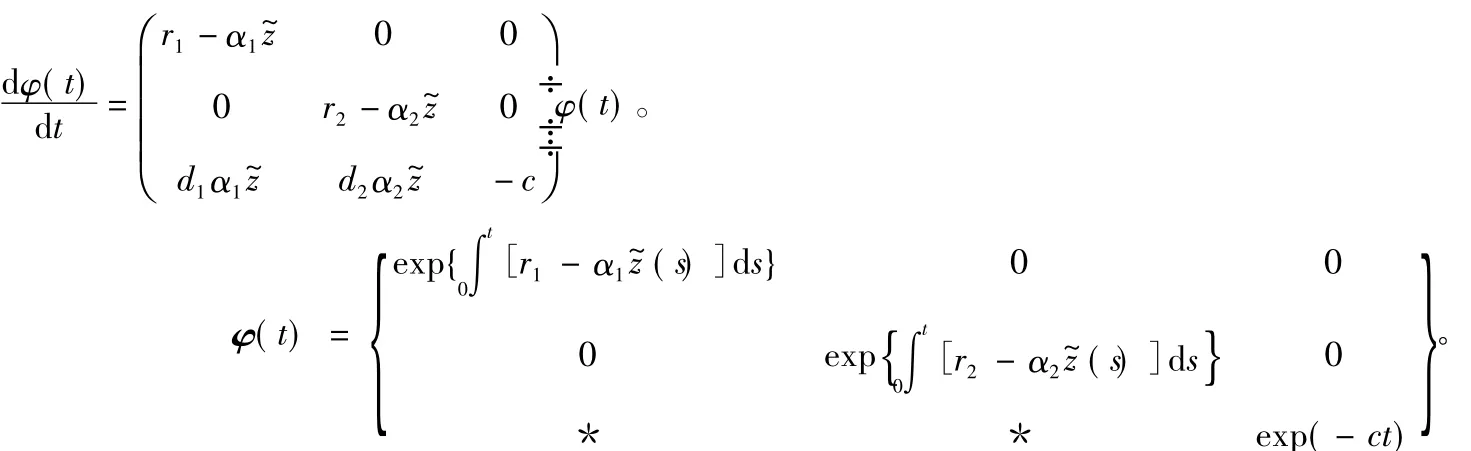
后面没有用到*处的值，因此此处不须要计算。对应的脉冲条件为

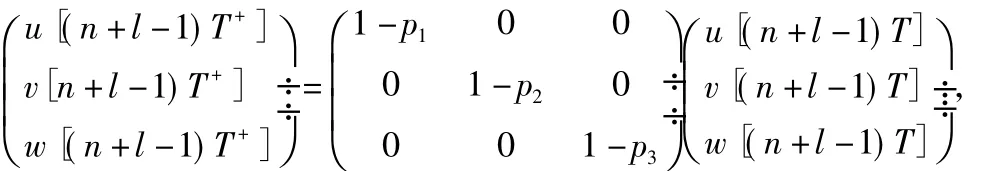
因此基解矩阵为

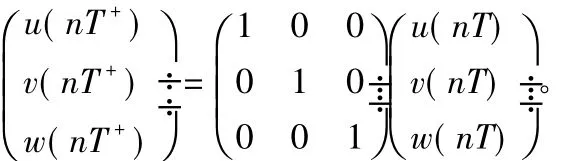
可得单值矩阵

当 λ1、λ2满足|λ1|＜1 且|λ2|＜1 时，根据 Floquet理论可知，2类食饵全部灭绝周期解［0，0，z～(t)］是渐近稳定的。而|λ1|＜1且|λ2|＜1的充要条件是 f1(T) ＜0，f2(T)＜0。由于fi(0)=ln(1－pi)＜0，fi(T)→∞ (T→∞)同时f″i(T) ＞0，则 fi(T)=0 有唯一的正根 Ti。当 T≤min{T1，T2}时，f1(T)＜0，f2(T)＜0。因此定理1得证。

定理2 设［x1(t)，x2(t)，z(t)］为模型(2)的任意解，如果满2类食饵全部灭绝周期解［0，0，z～(t)］是全局渐近稳定的。其

证 明:选 取 ε ＞0，使 得 η =(1－p1)exp模型(2)可得

利用脉冲微分方程比较定理有x1(t)≤u1(t)，其中u1(t)为下式的解:

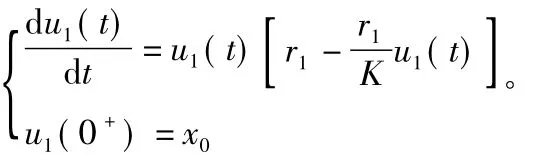
因此，有 x1［(n+l)T］≤x1(lT)ηn，其中 η =(1 －p1)exp0(n→∞)。同时当 t∈［(n+l－1)T，(n+l)T］时，有0≤x1(t)≤x［(n+l－1)T］(1 －p1)erT。

因此x1(t)→0(t→∞)。

同理可得 x2［(n+l)T］≤x2(lT)δn，其中 δ=(1 － p2)exp0(n→∞)。同时当 t∈［(n+l－1)T，(n+l)T］时，有0≤x2(t)≤x［(n+l－1)T］(1 －p2)erT。

因此x2(t)→0(t→∞)。

证明:当t→∞时，z(t)→z～(t)。取充分小的正数ε1＞0，存在 T'＞0，使得当 t≥T'时，有0 ＜x1(t) ＜ ε1，0 ＜x2(t) ＜ ε1，于是:

3 数值模拟

由于fi(0)=ln(1－pi)＜0，fi(T)→∞(T→∞)，同时f″i(T) ＞0，因此fi(T)=0 有唯一的正根 Ti(i=1，2)，且当T≤min{T1，T2}时，公式(5)成立。同理gi(T)=0有唯一的正根析得到min{T^1，T^

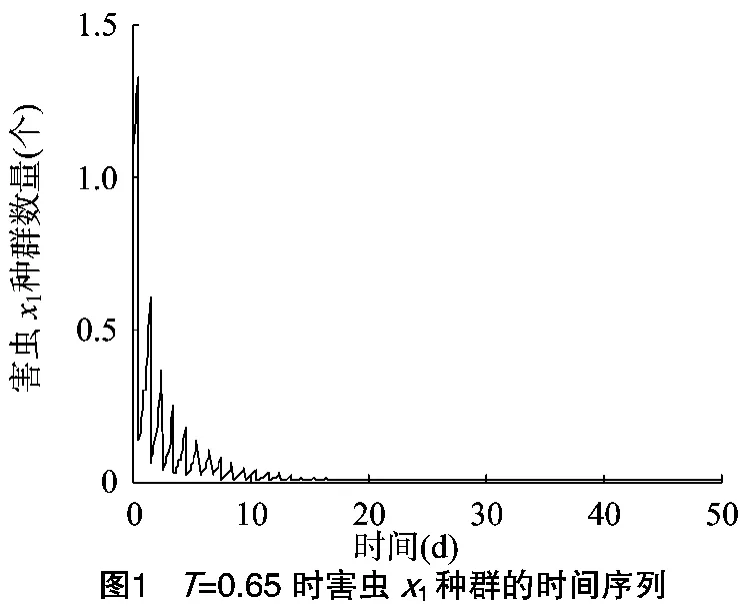
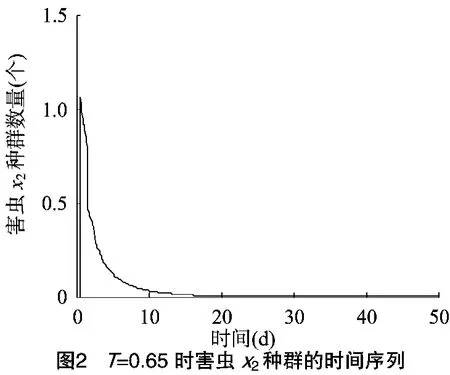
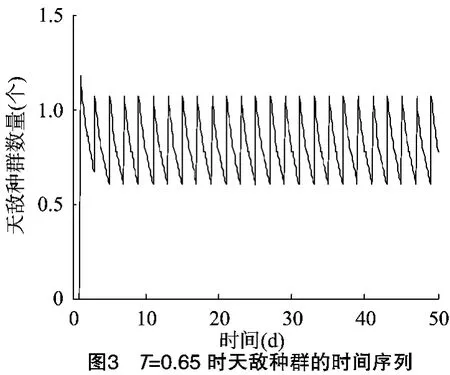
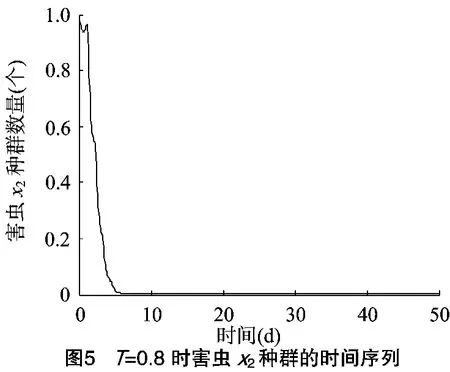
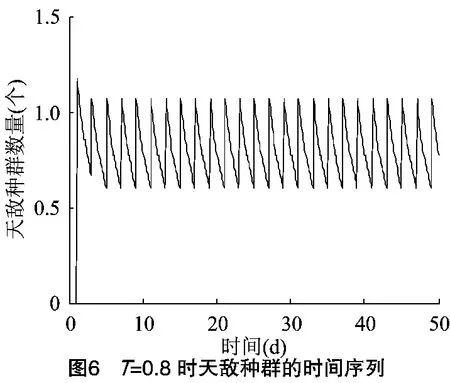
2} ＜min{T1，T2}，利用Matlab软件进行数值模拟，将模型(2)中的参数取值为 r1=3，r2=4，K=1.5，u=5，l=0.2，c=0.4，p1=0.7，p2=0.8，p3=0.2，w1=1，w2=2，α1=0.4，α2=0.6，由定理 1、定理 2 知，T1=1.6，T2=1.7，解［0，0，z～(t)］是局部渐近稳定的，结果与初值的选择有关。当T=0.65时，2类食饵全部灭绝周期解［0，0，z～(t)］是全局渐近稳定的，结果与初值的选择无关。此时2类食饵很快趋于零，而天敌出现周期性波动(图1至图3)。若0.7＜T=0.8＜0.9时，x2迅速趋于0，而x1与z出现周期性波动(图4至图6)。因此，若x2为主要食饵，x1为次要食饵，可以通过控制脉冲周期将主要食饵灭绝，保留次要食饵。

4 结束语

本研究建立了在不同脉冲时刻分别喷洒化学农药和投放捕食者的2个食饵1个捕食者模型，由脉冲微分方程理论得出模型(2)中食饵全部灭绝周期解稳定性成立的充分条件，并利用Matlab软件进行数值模拟。在实际中，此结论有广泛的应用，适用于所有的2个食饵1个捕食者情形。如在农业中，可以根据农田中天敌和害虫的具体情况，通过调节相应的参数改变脉冲周期，将2类害虫全部灭绝或将主要害虫灭绝，保留次要害虫，从而给出治理害虫的方法，达到保护植物以及提高农业产量的目的，具有重要的理论和现实意义。