GPS高程拟合在水利工程测量中的应用

孙昌瑜

(吉林省水利水电勘测设计研究院，吉林 长春 130012)

目前，随着经济的快速发展，GNSS(全球导航卫星系统)在各行各业都得到了广泛的应用。其在水利工程控制测量中，平面坐标的获取不仅时间短，且精度高，可直接应用，但在高程方面，GPS测量的高程是以WGS- 84参考椭球面为基准面的大地高H，而我国的高程系统是以大地水准面为基准面的正常高h。两者的转换关系为：

H=h+ζ

(1)

式中，ζ—高程异常。由于参考椭球面与似大地水准面之间关系复杂，导致ζ不能用某个确切的数学函数表示。因此，GPS所测高程在实际应用中受到了很大的限制。而正常高h大部分采用直接等级水准获得，其费时费力。如果要想利用GPS测得的大地高通过高程异常值直接换算为正常高而使用，那么所获取的高程异常值ζ的准确程度是非常重要的。

基于此，本文就求解GPS高程异常值的多项式曲面函数法、多面函数法进行了综合比较，得出了一些结论。使之为水利工程测量中正常高的获得提供一定的参考。

1 高程异常值求解的方法及精度评定

1.1 高程拟合的方法

1.1.1 多项式曲面拟合法

多项式曲面拟合的基本出发点是在拟合区域内，将大地高与正常高的重合点之间平滑出一个曲面来表示这个区域的似大地水准面，进而通过内插求出未知点的高程异常值，然后求出该点的正常高。此方法的特点为，伴随拟合区域面积的增加，拟合的高程异常变化增大，且伴随多项式阶次的增高，拟合曲面的波动也越大。多项式函数可表示为：

ζi=f(xi，yi)+εi

(2)

式中，ζi—高程异常值；f(xi，yi)—拟合曲面函数；εi—拟合残差。

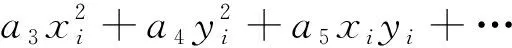
(3)

于是有：

(4)

式中，ai—未知参数。

当已知点个数大于等于参数个数时，在[ε2]=min条件下，求出各参数，然后利用式(2)可求出测区内任意点的高程异常。

(1)平面拟合法

当式(4)取一阶时，即为平面拟合，可表示为：

f(xi，yi)=a0+a1xi+a2yi+εi

(5)

将式(5)写成误差方程形式：

V=BX-L

(6)

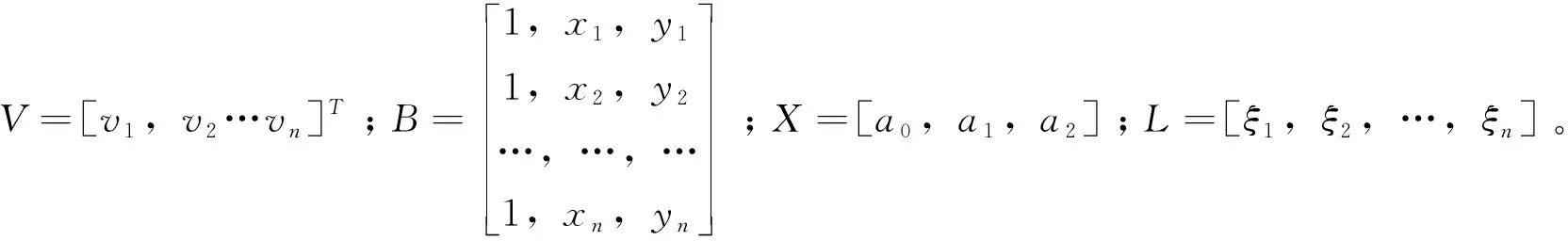
根据最小二乘法原理可求得拟合系数：

X=(BTB)-1BTL

(7)

然后再利用式(5)求得待求点的异常值。

(2)二次曲面拟合法

当式(4)取二阶时，即为二次曲面拟合，表示为：

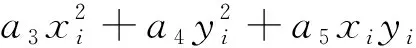
(8)

由式(8)可知，有6个未知参数a0，a1…a5。因此，至少需要6个已知点进而列出6个方程求解。若测区内的已知点的个数大于6个，多项式系数可通过最小二乘原理VTPV=min求得。

假设已知点数为n，由式(8)可列误差方程：

(9)

可表示为：

V=BX-L

(10)

式中，V=[v1，v2…vn]T；

由最小二乘原理VTPV=min，得到解为：

X=(BTB)-1BTL

(11)

然后在利用式(8)求得待求点的异常值。

1.1.2 多面函数拟合法

1971年，Hardy教授提出了多面函数法。其基本思想是：任何表面，都能用一定的有规则的数学表面通过叠加无限逼近。即每个插值点可以由已知点建立的函数关系叠加，组成新的函数关系[1]。多面函数可表示为：

(12)

式中，βi—待定参数；f(x，y，xi，yi)—x和y的二次核函数，其可表示成：

f(x，y，xi，yi)=[(x-xi)2+(y-yi)2+δ2]k

(13)

式中，δ2—光滑因子。当k=1/2时，称为正双曲面函数，当k=-1/2时，称为倒双曲面函数。

设有n个已知点(xi，yi)(i=1，1，…n)，取其中m(m≤n)个点作为核函数的核心数据，并设Qij=f(xj，yj，xi，yi)，则式(12)可表示为：

(14)

构建误差方程式为：

(15)

将其表示成向量形式为：

V=Qβ-φ

(16)

按照最小二乘原理得：

β=(QTQ)-1QTφ

(17)

在把求得的β带入式(12)就可计算待求点的异常值。此法的关键就在于核函数和光滑因子的确定。核函数的选取会拟合效果，光滑因子只能通过不断的试算进行确定。

1.2 精度评定

通常精度评定方法有方差、标准差等。鉴于高程拟合既存在拟合点也存在检核点，一般采用内符合精度指标θ1和外符合精度指标θ2来评价：

(18)

(19)

式中，v1—拟合高程异常的残差，n1—拟合点个数，v2—外推高程异常的残差，n2—外推点个数。内、外符合精度越小，表示拟合和推估的精度越高，其效果越好。

2 实例分析

为了研究以上方法在GPS高程拟合中的应用，对某水利工程D级GPS控制网联测了24个水准高程点，区域跨度约为55km，平面控制按照D级GPS网要求进行施测，高程按照国家四等要求进行施测，经稳健估计检验，数据不含粗差。这些点的分布如图1所示。

为比较平面拟合、二次曲面拟合、多面函数法拟合对求取的GPS高程异常值的效果。拟合所选取的公共点为Z16、Z17、Z12、Z10、D1、Z1、D4、D6-1、Z5、Z8十个点。由图1可知，这些点分布较均匀，可覆盖整个测区。其中，多面函数拟合法选择正双曲面函数，光滑因子经过不断试算，选取δ2=3600。各模型的计算均在MATLAB 2014b软件下编程实现。

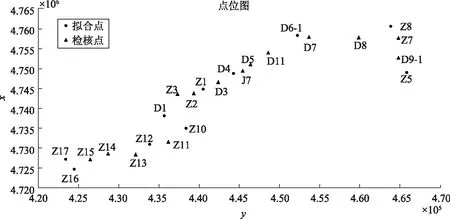
图1 点位分布图

采用3种方法计算的拟合点及检核点高程异常值和残差值，见表1、2。

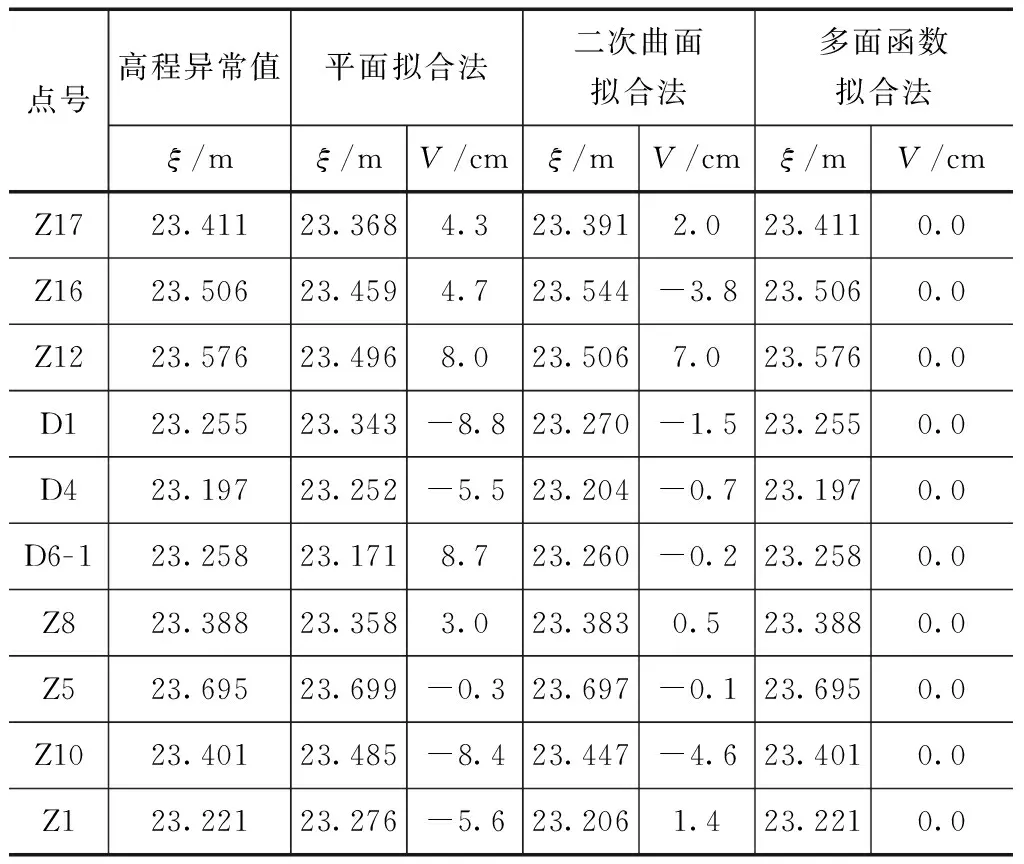
表1 拟合点高程异常值及残差

从表1、2可知：多面函数法拟合点的残差都为0，检核点的最大残差点为D8，差值5.2cm，其余各点残差都较小，且大部分都在3cm以内，拟合效果较好。二次曲面拟合法的拟合点的最大残差点为Z12，差值7.0cm，其余各点都较小，检核点的最大残差点为Z11，相差8.4cm，其余各点除了D8相差7.9cm外，拟合精度都较高。平面拟合法的拟合点的残差除Z5、Z8外，其余各点残差都较大，检核点的最大残差点为Z11，相差9.9cm，Z13、Z2、D3、J7、Z3、D8点检核残差也都较大，其余各点残差较小。造成此问题的原因在于拟合点Z1、D4、D6- 1分布近似于一条直线，致使拟合出的平面模型较差。因此，从拟合点、检核点的残差来讲，采用多面函数拟合法求得的高程异常值是最优的，其次为二次曲面法、平面拟合法。为了更加直观地体现不同拟合方法的检核点精度，各拟合方法的残差大小如图2所示。

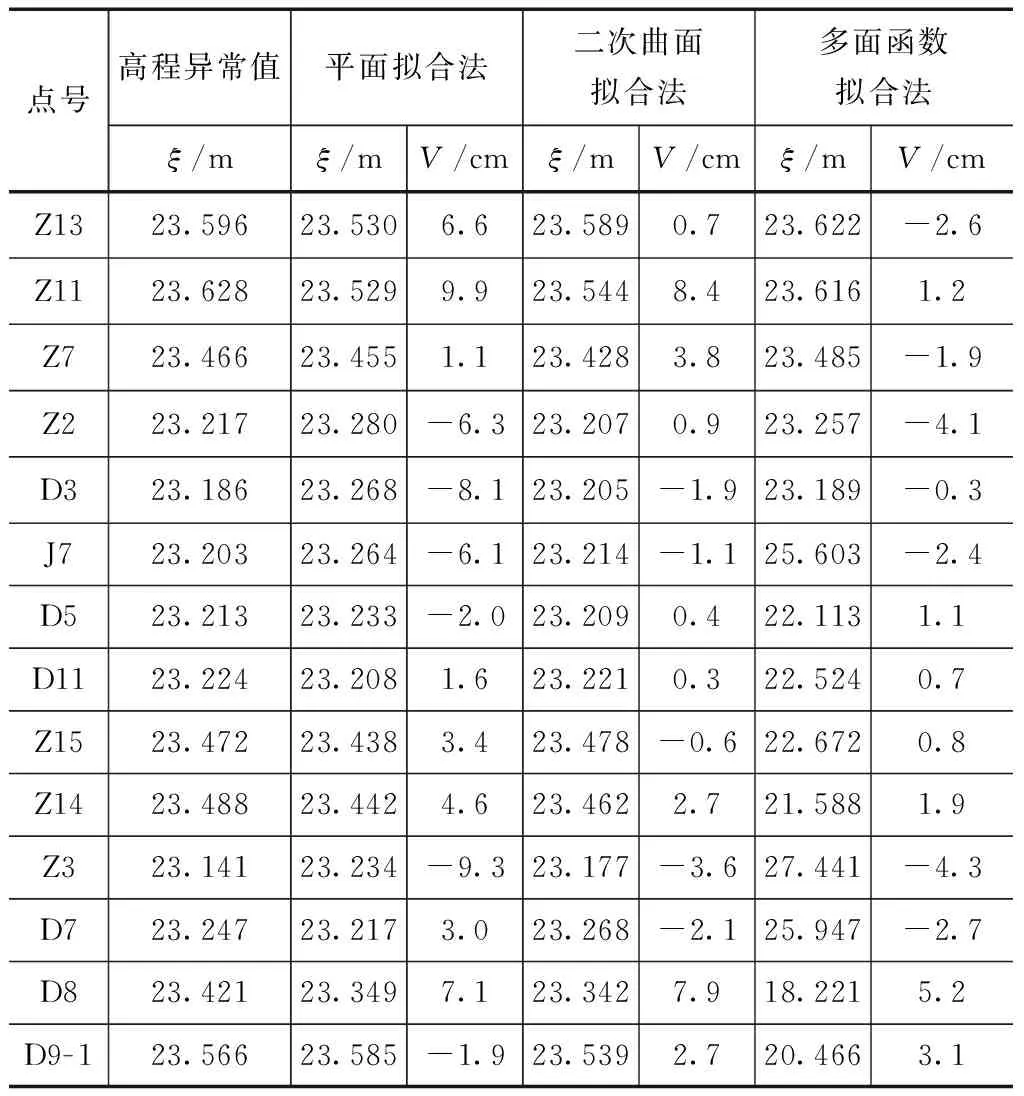
表2 检核点高程异常值及残差

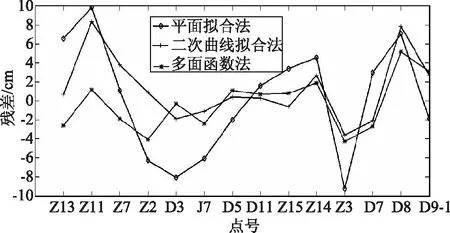
图2 不同拟合方法的检核点残差

由图2可知，多面函数法和二次曲面拟合法精度较高。为了从精度指标上分析各种方法的优劣性，计算各拟合法的内符合精度和外符合精度，其值见表3。由表3可知：多面函数法在内符合精度及外符合精度上都优于二次曲面拟合法和平面拟合法。

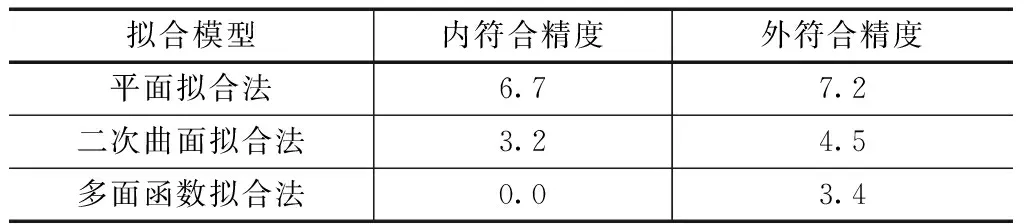
表3 各种模型的拟合精度 单位：cm

3 结语

平面拟合法对于所选拟合点除应均匀分布于测区外，其邻近的各点都应构成三角形平面，实例中，有几个点的分布近似于直线，致使其周围检核点的高程异常值与实际值偏大。这在今后运用此方法是应当注意。二次曲面拟合模型可较好地提取高程异常的趋势性，适应用于平坦地区，但在地形起伏变化较大的区域，拟合精度也难以保证。多面函数拟合法由于其建立的思想是用一定的有规则的数学表面通过叠加无限逼近真实表面，在高程拟合中就是用每个插值点与已知数据构建函数关系，从而计算最佳插值。因此，多面函数法拟合的精度较好，也可适当地应用于水利工程测量中，通过实例也证明了此方法的有效性。但本文多面函数法是基于正双曲面函数进行论证的，对其它函数没有进行比较分析，加之光滑因子的确定也是在大量的试算中确定的，没有统一的算法。这些在今后的研究中，可给予重视。