无定义参数条件下独立坐标系与标准坐标系的转换研究

刘明松,邱中军,刘忠贞

(1.吉林省水利水电勘测设计研究院测绘院，吉林 长春 130012；2.吉林省测绘职业资格管理中心，吉林 长春 130051)

某综合性大型水库位于东北某省一重要工业城市的南郊，是城区居民的重要水源地。该水库在建设、管理和维护运营中使用的地理信息成果均为1954北京坐标系，而该工业城市城区所有的基础地理空间数据以及相关规划设计、审批图件等成果均采用的城市独立坐标系。随着地理空间数据共享互通的大数据时代的到来，各组织各部门的数据交往越来越紧密，科学地实现两套坐标系下的数据转换和统一就十分的重要。但由于历史原因和处于保密的考虑，很难获取独立坐标系的定义参数，这使得独立坐标系向国家标准坐标系的精确转换困难重重。为了实现该水库地理信息数据与该市城市坐标系的互转，通过资料收集、数据试验以及精度分析，探讨在不具备独立坐标系定义参数的情况下，在局部区域实现坐标转换的方法，为从事相关活动的技术工作者提供参考。

1 独立坐标系及转换模型分析

1.1 独立坐标系分析

建立独立坐标系主要包括经行政主管部门批准的地方城市坐标系和为满足精度要求和使用方便所建立的工程坐标系两种情况。坐标系建立的方法主要有抵偿投影面的3°带高斯平面直角坐标系，任意带投影高斯平面直角坐标系，以应用区域中心经线为中央经线平均高程面为投影面的平面直角坐标系，假定平面直角坐标系等4种[1]。

独立坐标系的建立涉及该坐标系的投影椭球、中央子午线、抵偿高程面、起算方位角、原点等5大要素的选择和设定。在具体实践中会根据应用区域内的具体地理地形地貌环境以及地理空间数据采集的精度需要，特别是在城市测量中规范要求保证坐标系内坐标投影后边长变形不大于2.5cm/km，选择不同的方式完成坐标系的定义。理论上讲，要实现独立坐标系真正意义上的坐标转换，就必须获取真实可靠的坐标系定义五要素的参数。

1.2 转换模型分析

独立坐标系的标准坐标转换，本质是在获取独立坐标系定义参数的前提下，首先完成同参考椭球无精度损失的标准坐标系空间物理恢复，然后在不同参考椭球中实现不同标准坐标系数据的空间坐标转换等两大步骤。因此独立坐标系的数据转换与标准坐标系不同参考椭球间的转换没有理论性的区别[2- 3]。但现实是很多独立坐标系都无法获取坐标系定义的参数，也就无法将独立坐标系原原本本的还原到该坐标系同椭球下的标准坐标系中，参考椭球和抵偿高程面以及投影经线等定义参数的未知意味着独立坐标系只能使用二维平面的方式实现坐标系的转换。

目前，二维平面转换模型包括二维四参数平面坐标转换模型和平面多项式拟合模型两种。二维四参数坐标转换模型是一种物理模型[4]，公式如下：

(1)

式中，x1、y1—原坐标系下平面直角坐标；x2、y2—新坐标系下坐标；Δx、Δy—平移参数；α—旋转参数；m—尺度参数。

平面多项式拟合模型是一个种纯数学模型[5]，公式如下：

x2=x1+Δx

y2=y1+Δy

(2)

式中，x1、y1—原坐标系下平面直角坐标；x2、y2—新坐标系下坐标；Δx、Δy—坐标转换改正量，计算公式为：

Δx=a0+a1x+a2y+a3x2+a4xy+a5y2+a6x3+a7x2y+a8xy2+a9y3+…

(3)

Δy=b0+b1x+b2y+b3x2+b4xy+b5y2+b6x3+b7x2y+b8xy2+b9y3+…

(4)

式中，ai，bi—系数(i=0，1，2…)，通过最小二乘求解。

从以上2个公式可以看出，二维平面转换模型是基于投影后两种平面直角坐标系间的数据关系进行的坐标转换，该转换模式没有考虑椭球的曲面影响，因此转换精度受到地理空间位置、应用区域的大小以及形状的影响。利用以上2种模型能否实现在本研究区域这一局部范围内完成该市城市坐标系到1954北京坐标系的转换，哪套模型转换精度更优，是关系能否快捷方便的实现研究区域该水库数据与该市城市主体性的基础地理空间数据成果互通，共享的关键。需要通过方案设计和数据实验来判断该两种模型的适应性。

2 坐标转换方案设计与数据实验

2.1 转换方案设计

从理论上讲，受球面影响二维平面坐标系转换模型只适用于局部的小区域数据转换，因此，实验方案应考虑以下内容：

(1)针对研究区，进行充分的地理空间位置环境对坐标系定义要素的影响分析。结合基础资料的收集，研究转换方案实验的可行性。

(2)两种模型转换计算数据成果的可靠性。要求计算转换参数的公共重合点几何结构合理，计算模型使用科学，精度验证方法科学。

(3)两种模型转换优劣的比较。在同等地理空间位置和外部条件下，分析对比不同模型的差别和特点。

(4)应用需求条件验证完整全面。将项目生产中可能应用的情况进行全面的实验，总结模型使用的适应规律。

根据1.1节的介绍，在局部区域影响独立坐标系投影反算边长精度最重要坐标定义参数为投影面以及投影经线两个要素[6]。其中独立坐标系抵偿高程投影面多数情况下采用的方法为参考椭球的放大或缩小，对边长的影响只成简单比例关系；而投影经线受高斯-克吕格投影特点的影响，离中央经线越远变形越大，因此中央经线的合理性对精度影响更大更复杂。研究水库位于该市城区正南郊环城高速外约10km，南北长约20km，东西宽约6km。城区中轴线经度大约为125°19′，库区与其基本接近，该经线与标准3°分带的高斯投影中央子午线126°距离偏近，形成的投影反算边长误差影响相对较小，从研究区的地理空间位置上看，有利于二维平面模型的使用。

通过基础资料收集和实地踏勘，共获得研究水库区域内D级控制点11个，根据这些控制点空间分布情况，结合坐标转换的具体需求，对实验方案进行布局，主要完成以下3个方面的实验设计：

(1)转换模型参数计算的可靠性实验。已获得的11个控制点均分布在库区的四周，能够完整的实现对库区的包围，其点位间距在3～5km之间分布较为均匀。将所有的点参与计算有利于提高参数客观性，提高残差精度。

(2)库区内坐标转换精度评价实验。坐标转换的目的是对已有地理信息成果的坐标系关联，在转换参数求解区域内完成其他地理信息数据的转换，是数据转换的基本需求。

(3)库区外坐标转换适应性实验。随着实际项目生产需求的变化，往往可能会在原有项目区外延工程，验证转换参数求解外延区域坐标转换精度情况，有利于扩大转换模型使用范围，确定模型的使用适应性边界。为了保证外延实验精度效果，特意在库区正北约同一经度附近选择4个检测点，离库区北侧约10km。

研究水库已有控制点和新选择的外延检测点的空间分布如图1所示。其中以“XG”为标识为库区控制点，“S”标识为检测点。为了获得更加可靠的实验结果，对以上共计15个点，进行了城市坐标系和1954北京坐标系的高精度数据采集，其数据成果见表1。

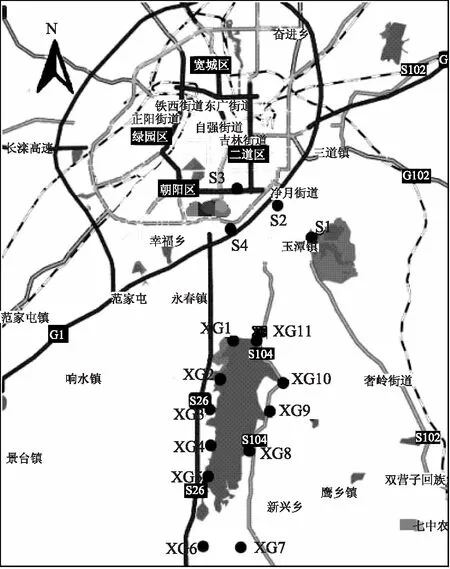
图1 坐标转换基础数据采集分布

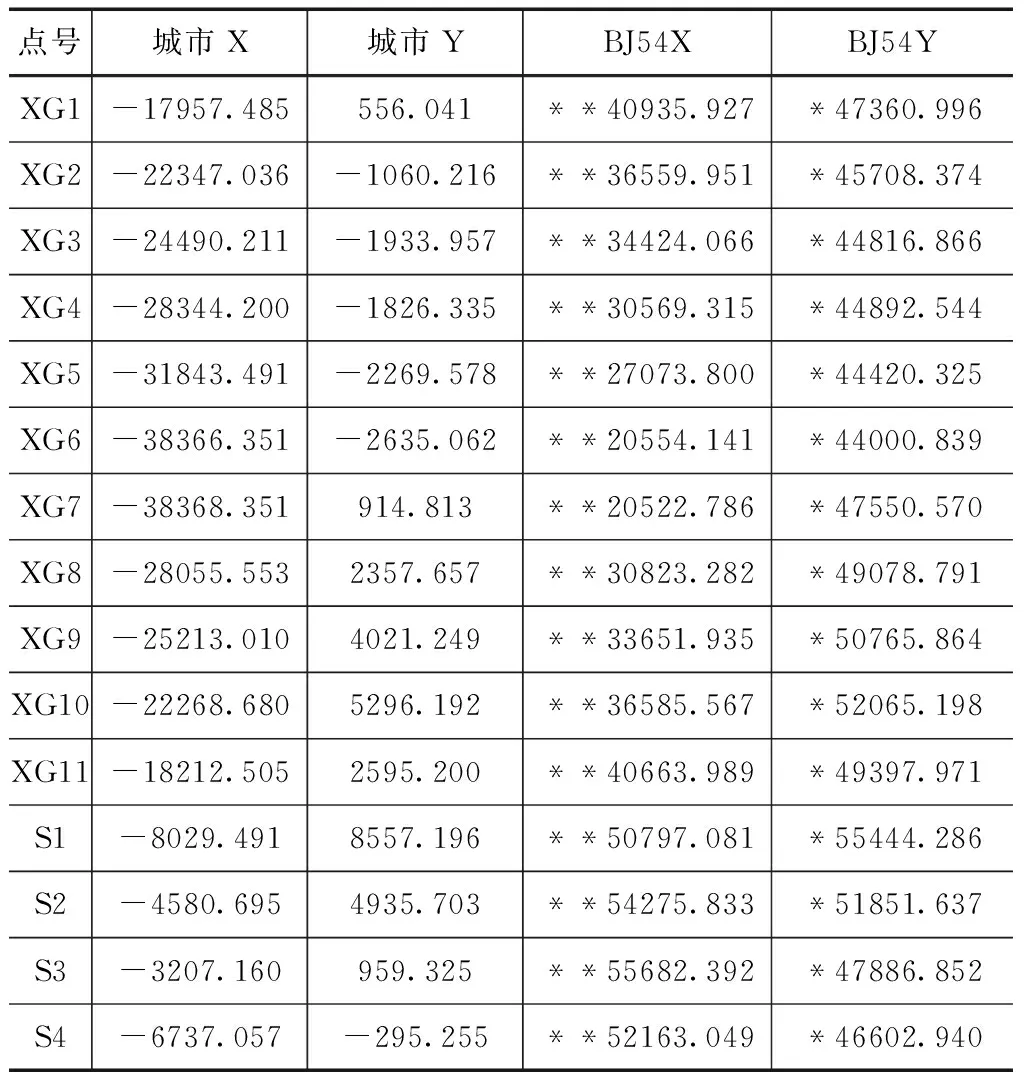
点号城市X城市YBJ54XBJ54YXG1-17957.485556.041**40935.927*47360.996XG2-22347.036-1060.216**36559.951*45708.374XG3-24490.211-1933.957**34424.066*44816.866XG4-28344.200-1826.335**30569.315*44892.544XG5-31843.491-2269.578**27073.800*44420.325XG6-38366.351-2635.062**20554.141*44000.839XG7-38368.351914.813**20522.786*47550.570XG8-28055.5532357.657**30823.282*49078.791XG9-25213.0104021.249**33651.935*50765.864XG10-22268.6805296.192**36585.567*52065.198XG11-18212.5052595.200**40663.989*49397.971S1-8029.4918557.196**50797.081*55444.286S2-4580.6954935.703**54275.833*51851.637S3-3207.160959.325**55682.392*47886.852S4-6737.057-295.255**52163.049*46602.940

2.2 数据实验

2.2.1 参数计算可靠性实验

将库区内所有的11个已知控制点(XG1～XG11)参与到两个模型的计算中，获得二维四参模型和多项式拟合模型的转换参数，并利用该参数将11个点从城市坐标系转换到1954北京坐标系，计算转换坐标与原坐标间的较差，验证转换模型的可靠性。坐标差值见表2、3。

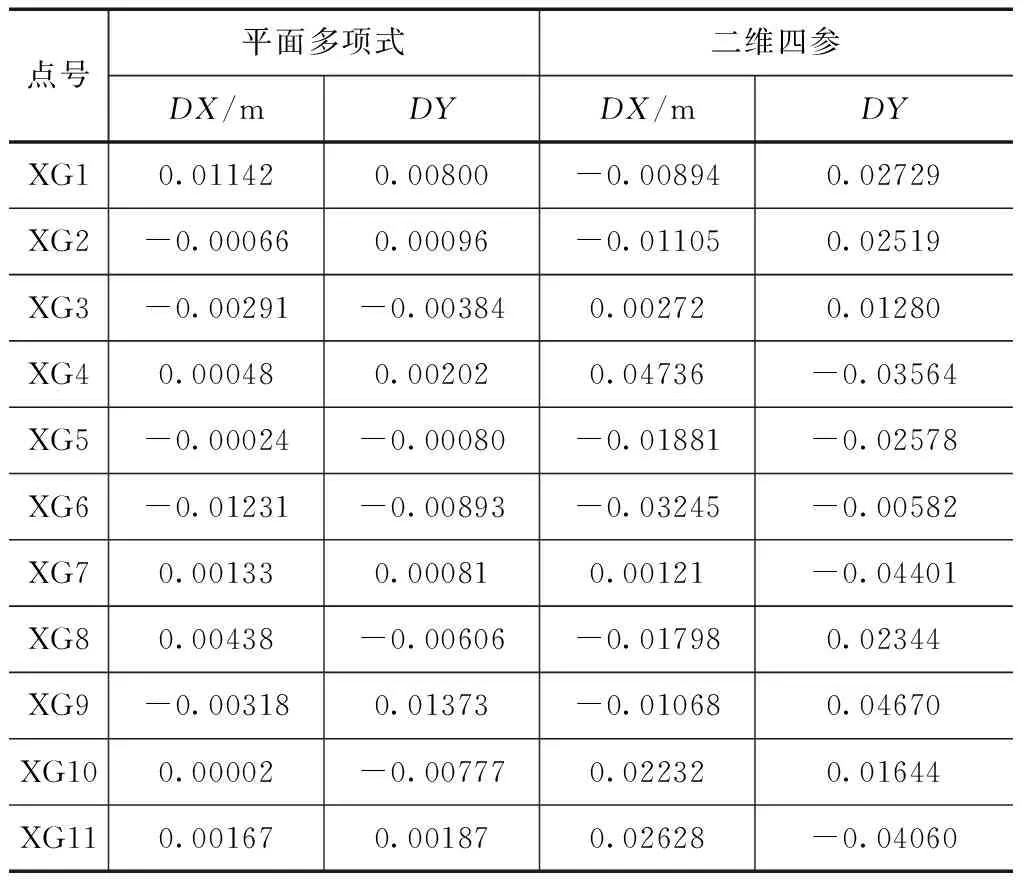
表2 坐标转换较差表

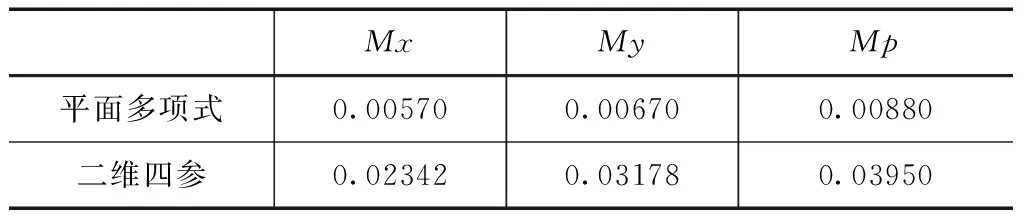
表3 坐标转换极限较差表

从表2、3可以看出，2种转换方法所获得精度都达到厘米级，但是多项式拟合转换精度更高，多数点都能达到毫米级，转换后精度损失更小。

2.2.2 库区内坐标转换精度评价实验

在库区的控制点中选择覆盖全面分布均匀的XG1、XG4、XG6、XG7、XG8、XG11等6个点进行转换参数的计算。通过计算获得的参数完成XG2、XG3、XG5、XG9等点的坐标转换，计算2个模型转换坐标与已知坐标的差值，判断2个模型的优劣特点。计算结果见表4。

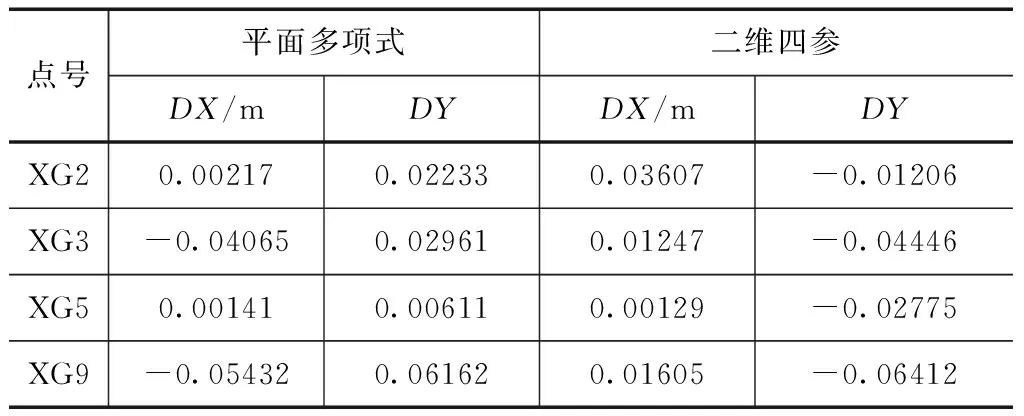
表4 参数控制区域内检测点较差计算表

依据表4可以得出平面多项式拟合平均点位较差为3.8cm，二维四参平均点位较差为4.1cm。2个模型的转换精度基本相当，没有明显的优劣。

2.2.3库区参数计算区域外延坐标转换适应性实验

为了研究实验转换参数完成外延区坐标转换的能力，在研究库区与城区之间选择了S1、S2、S3、S4等4个检测点，该组点离库区最近处约10km且尽量处于同一经度区域内，利用库区控制点计算的转换参数实现对该组点的坐标转换，计算转换后与已知坐标的较差，计算结果见表5。

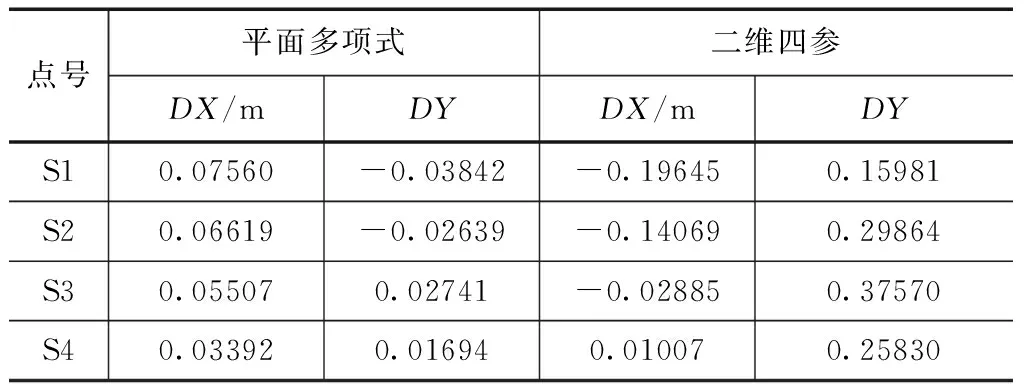
表5 外延检测点较差计算表

从表5可知，多项式拟合转换计算点位较差为5.8cm，二维四参数转换为28.7cm。很明显可以看出，虽然两种模型都随着参数计算区域的远离误差变大，但是平面多项式拟合模型精度影响较小，二维四参数模型影响很大，二维四参模型的计算应用区域更小更窄。

2.2.4 实验总结

从以上分析及实验结果可以获得以下规律：

(1)在小区域内利用二维平面模型完成独立坐标系到标准坐标系的转换，其精度可能达到厘米级。

(2)在参数计算区域外延地区利用二维平面模型转换坐标，随着离参数区域的距离越远，精度越低。二维四参数法转换精度下降极快，外延范围有限；多项式拟合模型在10km以内仍然能够达到厘米级精度。

(3)应加强作业区域地理空间分析，适当综合利用大地空间模型尽量搜索恢复独立坐标系的投影面、投影经线以及定向角度，使该坐标更接近于国家标准坐标系统后实施二维平面模型的坐标转换，以提高数据计算的精度。

3 结语

笔者在某区域具体工程项目中进行研究和实验，讨论在未知定义参数的条件下，利用二维平面转换模型完成独立坐标系到国家标准坐标系转换的可行性。通过比较分析，总结出在局部区域内平面多项式拟合模型比二维四参数模型适应区域更大、外延精度衰减更慢的规律，为从事类似工作的技术人员提供参考。