采用改进的希尔伯特黄变换的损伤检测特征提取方法

张涛,丁碧云,赵鑫

(天津大学电气自动化与信息工程学院,300072,天津)

音频信号中含有大量的信息,特征提取是有效获取信号中关键信息的重要途径。损伤检测是一种通过分析被测物体受外界激励(如敲击)产生的响应(如声波)来判定被检测对象是否存在损伤的技术。其中,敲击检测的方法是最简单常用的一种,该方法依靠物体振动特性实现损伤检测,相比于其他损伤检测方法,具有操作简单、检测速度快、受环境影响小和成本低等优点[1]。在损伤检测过程中,合适的特征提取方法是损伤检测的关键环节,它直接影响检测的准确性和可靠性。损伤检测中常用的特征提取方法有:①时域分析方法,包含有量纲的过零率和短时能量特征,无量纲的均值、峰值、方差、均方根值、峰值因子、脉冲因子、裕度因子、波形因子、K因子、峭度以及自相关分析参数等特征[2];②频域分析方法,包含频谱峰值、频谱位置和频谱面积等特征[3];③小波分析法,包含各节点的能量和方差等特征[4]。

音频信号作为典型的非线性、非平稳信号,具有较强的时变性。传统的音频特征提取方法不能同时满足时间和频率分辨率的要求,难以精确地提取信号的时间和频率特性。因此,一般采用时频分析方法来分析非平稳、非线性信号。常用的时频分析方法有短时傅里叶变换、Wigner-Viller分布、小波变换,这些方法虽然能够较好地分析音频信号的时频特性,但也存在一些问题,如短时傅里叶变换存在受Heisenberg测不准原理限制和单一分辨率问题,Wigner-Viller分布存在严重的交叉干扰项问题,小波变换存在过分依赖小波基选取和能量泄露等限制[5]。1999年Huang等提出了一种具有自适应性、局部性、完备性与近似正交性的新型时频分析方法——希尔伯特黄变换(Hilbert-Huang Transform,HHT)[6]。HHT方法由经验模式分解(Empirical Mode Decomposition,EMD)和Hilbert变换两部分的组成。EMD分解将待分析信号分解为若干个固有模式函数(Intrinsic Mode Function,IMF),又称IMF分量。IMF分量能够克服Hilbert变换存在负值频率的问题,得到具有物理意义的正数瞬时频率,从而实现准确的时频分析。HHT方法的不足之处在于HHT方法在EMD分解过程中存在着包络拟合、模态混叠、端点效应和虚假IMF分量等问题,导致HHT方法最终分析结果存在一定的误差。

本文主要针对HHT方法中的模态混叠和虚假IMF分量问题,提出了一种基于小波包分解和IMF分量筛选的改进HHT方法。首先对信号进行小波包分解与重构预处理,对重构信号进行EMD分解,再筛选IMF分量,最后对筛选后的IMF分量做Hilbert变换,得到信号的瞬时属性。采用玻璃瓶的无损敲击音频信号为实验数据,BP神经网络为分类器,实验验证了改进HHT方法的有效性和优势性。

1 损伤检测

损伤检测可以通过分析物体的响应信号来检测目标是否存在损伤,甚至是确定损伤位置,从而帮助人们对目标物体进行实时检测,降低生产过程的不必要损耗,减少经济损失。物体结构损伤研究表明,当物体结构存在某种损伤时,它的某些微结构属性会发生改变,并且这种变化与损伤的类型和程度都有密切的联系。然而,这些属性的直接测量难以与物体的宏观力学行为相联系,很难应用到实际工程中。由于材料的微结构状态决定了其宏观物理行为,因此可以通过监测物体的宏观物理行为间接测量物体的损伤状态和程度。实际应用中通常通过它们的动态响应确定损伤的状况,如物体受外界激发产生的声音。结构的损伤对信号的幅值和频率都有影响,会使信号的时域和频域特征存在差异,因此可以根据这些特征来判断被测物体是否存在损伤。损伤检测就是通过物体模态参数(频率和振型)检测损伤的发展规律来实现的[7]。

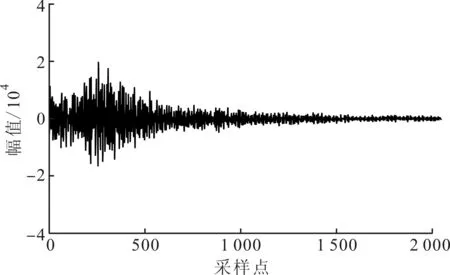
(a)有损伤玻璃瓶信号的时域波形

(b)有损伤玻璃瓶信号的频谱

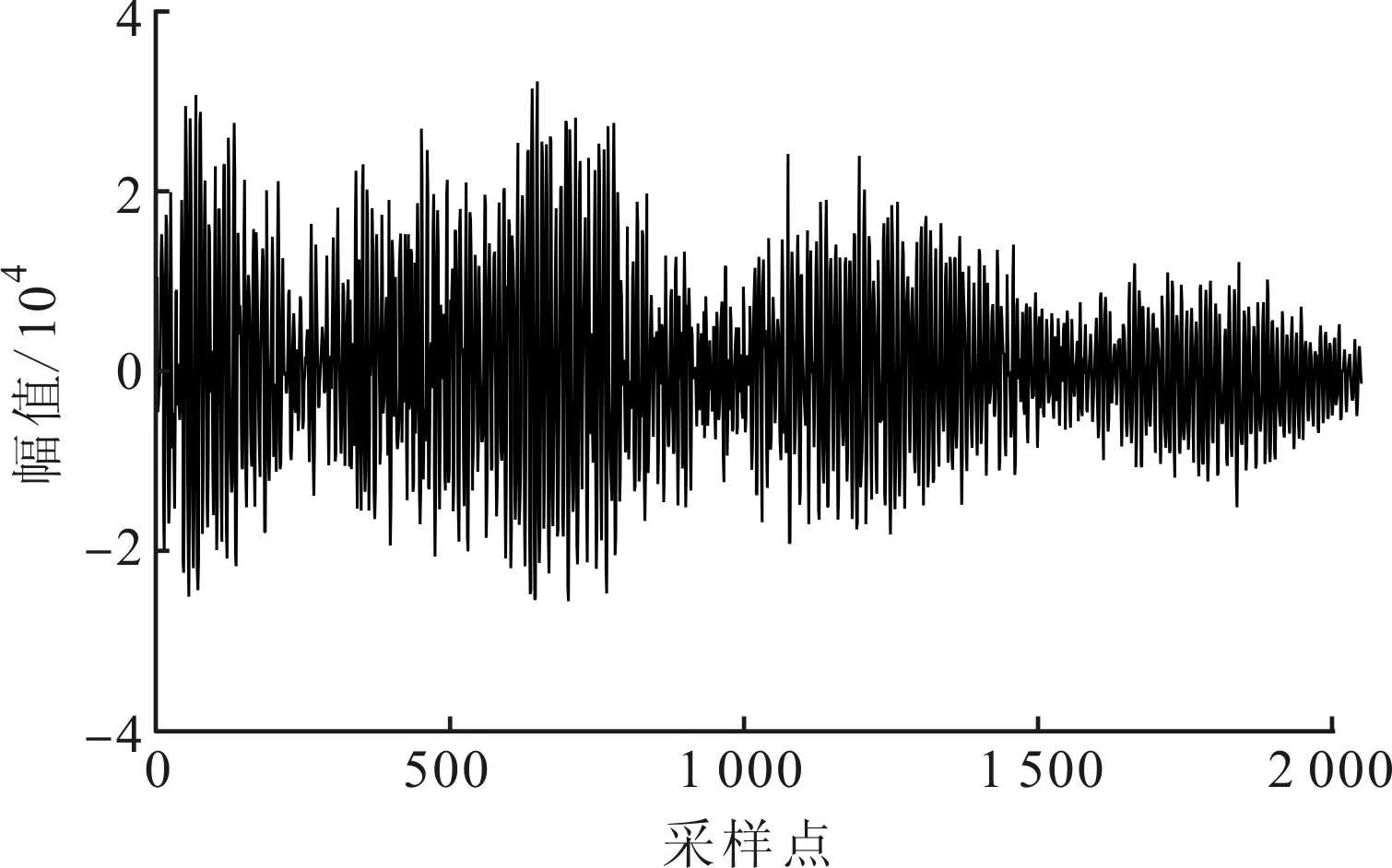
(c)无损伤玻璃瓶信号的时域波形

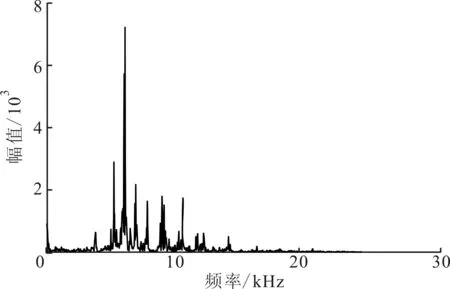
(d)无损伤玻璃瓶信号的频谱图1 有、无损伤玻璃瓶信号的时域、频域波形

损伤检测系统包括4个主要步骤:①通过敲击或其他方法使被测物体产生动态响应(如声波);②收集动态响应并通过传感器将其转换为电信号;③提取包含物体损伤信息的特征;④使用所提取的特征训练分类器建立分类模型,使用该模型进行损伤检测。本文通过分析敲击玻璃瓶产生的音频信号,检测玻璃瓶是否存在结构损伤,实验结果如图1所示。图1a、1b分别是敲击有损伤的玻璃瓶产生的声音信号的时域和频域波形图,图1c、1d则是敲击无损伤的玻璃瓶产生的声音信号的时域和频域波形图。

对比图1中的波形可知,玻璃瓶的损伤会使其激励产生的音频信号的时域幅值、频率分布等相关特征发生变化。这说明音频信号的某些特征包含损伤信息,通过分析这些特征,能够有效地判断目标物体是否存在损伤。本文主要研究损伤特征提取部分,针对损伤特征的可区分性,提出有效的解决方法。

2 改进的HHT方法

为了有效提取音频信号中的损伤特征,本文提出一种改进的HHT方法。首先采用小波包变换(wavelet packet transform,WPT)作为预处理方法,将信号分解成一组窄带信号。然后对所有的窄带信号分别进行EMD分解,此时得到的IMF分量可以真正成为单频成分。之后,通过剔除所有的IMF分量中不相关的虚假IMF分量,得到真实的IMF分量,从而减少信号分析的误差。因此,改进的HHT方法是一种可以用于非线性和非平稳信号分析的精确方法。

2.1 HHT方法

HHT方法包括EMD分解和Hilbert变换两部分。首先,EMD分解将待分析信号分解为一系列频率由高到低的IMF分量。IMF分量是对分析信号的一种完整的、自适应的和几乎正交的表示。IMF分量需要满足两个条件:①整个数据范围内,极值点与过零点的数目必须相等或者最多相差一个;②所有极大值点形成的上包络线和所有极小值点形成的下包络线的平均值始终为0。由于IMF分量几乎是单频成分,可以根据IMF分量从非线性、非平稳信号中计算所有瞬时频率,且每个瞬时频率的局部能量可以通过希尔伯特变换计算得到。因此,HHT方法的分析结果是信号的能量-频率-时间分布。由于HHT方法的计算过程复杂度不高,HHT方法在处理非线性、非平稳信号方面得到了较广泛的应用。然而,根据前人的实验研究,发现HHT方法的分析结果存在以下不足:①EMD会在低频部分产生一些不足以反映信号本身特征的虚假IMF分量[8];②若待分析的信号频带太宽,会出现较严重的模态混叠问题,得到的IMF分量可能覆盖太宽的频率范围,难以得到单频成分的IMF分量,最终造成频率物理意义不清晰;③由于EMD分解是基于信号本身分解的,EMD分解不能分离包含低能量成分的信号[9]。

音频信号作为一种非线性、非平稳的信号,含有较丰富的频率成分,其频带较宽。由于HHT方法本身的不足,常规的HHT方法很难对音频信号进行精确的分解,且存在虚假IMF分量、模态混叠等问题。针对上述问题,可先对信号进行初步的频率划分,降低EMD分解信号的初始带宽,以便得到单频成分的IMF分量,从而更加精确地分解音频信号。Peng等人曾提出结合小波包分解的改进HHT方法[9],并基于IMF分量与原信号的互相关系数筛选IMF分量,但是没有详细讨论小波包分解的相关参数,如小波基和分解层数等。本文针对这两部分进行了详细的研究,并提出了一种更有效的IMF分量筛选方法。

2.2 小波包分解

小波包理论是小波变换的推广,小波包分解可以对信号高频部分做进一步地分解,能将信号频带进行多层次的划分,自适应地将信号分解到不同的频段上,具有精确细分的特点和较强的时频局部化能力,能很好满足信号频率初步划分的要求[10]。以3层小波包分解为例,用变量S表示被分解的信号,S信号在第1层小波包分解中,被分解为低频分量L和高频分量H;在第2层小波包分解中L被分解为L0和L1,H被分解为H0和H1;在第3层小波包分解中,L0被分解为L0,0和L0,1,L1被分解为L1,0和L1,1,H0被分解为H0,0和H0,1,H1被分解为H1,0和H1,1。小波包分解信号的过程如图2所示。S信号分解具有如下关系

S=L0,0+L0,1+L1,0+L1,1+H0,0+

H0,1+H1,0+H1,1

(1)

利用小波包分解与重构能够得到不同频段范围的音频信号,再对各频段信号进行分析和处理,提取时频特征,是获得关键特征的有效方法。在小波包分解的实际应用中,小波基的选取和分解尺度的确定是小波包分析中最重要的问题。

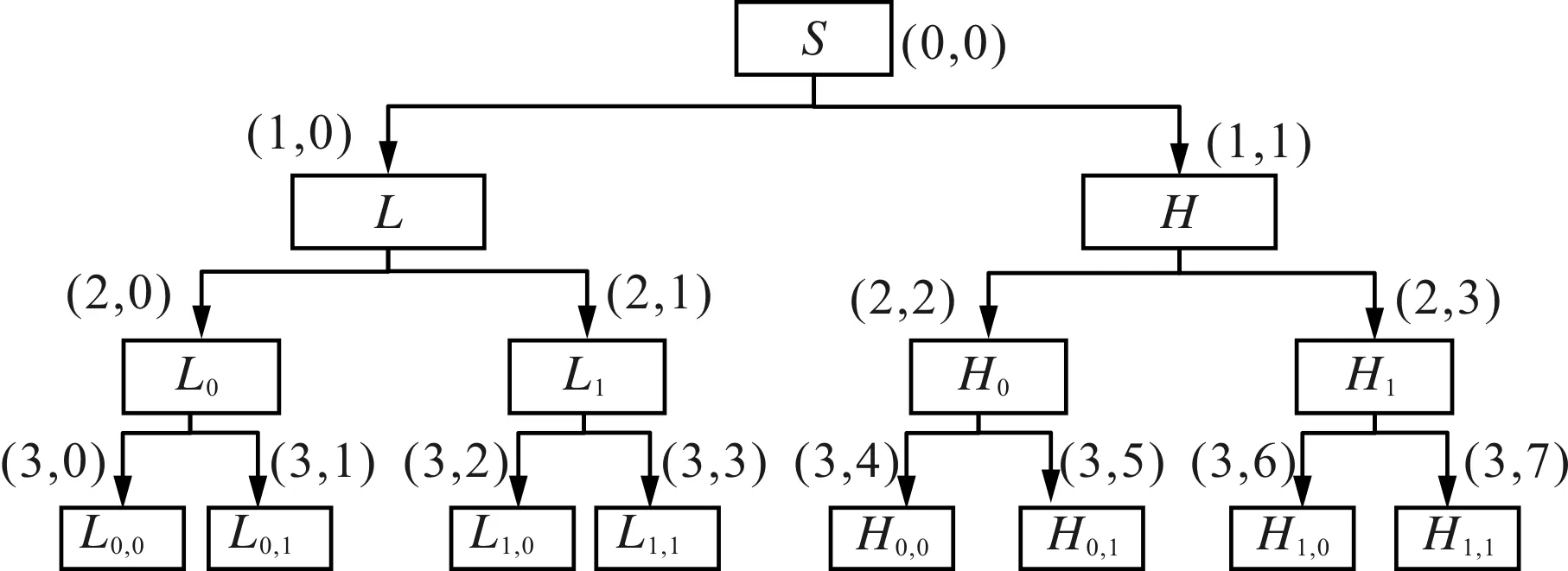
图2 小波包分解过程示意图

2.2.1 小波基的选取 一般地,不同的小波包基具有不同的时频局部化能力,反映不同信号的特性[11]。因此,对于给定的音频信号,选择一个合适的小波基是十分重要的。小波的主要参数包括其正交性、支撑集、正则性和对称性等,需要根据不同的应用选择合适的小波。目前还没有对小波选择的的完善理论指导,选取小波存在一定的困难。

一般来说,小波包分解系数之间的差别越大,就越容易提取信号的特征,此时采用的小波基就越好。在选取最优小波基之前,会定义一个代价函数,代价函数最小就是最优的数学表示。目前使用最多的是香农熵作为最优小波基的代价函数[12]。Bhuiyan等人提出基于最大化小波包分解节点能量的方法选取最优小波基[13];文献[14]中提出选取的小波基函数应与被提取的频率段相近。依据该方法,本文从Daubechies小波族中选取合适的小波基。由于待处理的音频信号的频谱范围为500 Hz～12 kHz,而db6小波的频谱范围为0～11.26 kHz,与被提取的频率相近,故选用db6小波作为小波包分解的小波基。

2.2.2 分解层数的选取 在很多小波包应用的实验中,分解层数一般不超过6[11],因此小波包分解层数一般选为2～6层。一般来说分解层数与需要被提取的频率段有关,分解层数的确定根据被测信号具有区分性的频率来确定。根据信号的频域特征,无损伤信号的第一个频谱峰值集中在4～15 kHz,有损伤信号的集中在1～4 kHz;无损伤信号的第2个频谱峰值主要集中在3～6 kHz,有损伤信号的集中在1～3 kHz。本文主要是检测信号中存在的损伤信息,由上述分析可知有损伤的信号频率主要集中在1～4 kHz。结合db小波的频带分解特点,在采样频率fs=48 kHz的情况下,分解至第n层后,可将信号分解到(0,fs/2)的2n个等频子频带上。由上述可知,损伤信号的频率主要集中在第3层的(0,fs/2n+1)和(fs/2n+1,fs/2n)两个低频带上。

2.3 IMF分量筛选指标

由于EMD分解过程中存在虚假IMF分量,在实际应用中,需要剔除这些虚假的IMF分量。真实IMF分量与原始信号的关联性比虚假分量与原始信号的关联性大,且真实IMF分量占的比例较虚假IMF分量要大。目前较常用的剔除虚假IMF分量的方法有相关系数法、灰度关联度法、互信息量(Mutual Information,MI)法、能量比值法、K-S检验法等。其中,灰色关联度是灰色关联分析方法描述系统各因素之间关联程度的量化指标;K-S检验[15]是寻找实际分布与理论分布之间的最大距离,适用于大样本,K-S检验法的相似概率对波形的形状差异非常敏感。这两种方法对于单成分信号能够较好地区分虚假IMF分量,但是对于多成分的复杂信号则难以区别。相关系数法[16]和能量比值法对信号的幅值依赖性较大,不利于虚假IMF分量的区分,而互信息量(MI,用符号IMI表示)能够较准确地统计IMF分量与原始信号的关联性,对于区分虚假IMF分量具有一定的优势。

IMI描述了两个随机变量之间的相关程度,通过IMI可以衡量两个变量间存在的共同信息量的多少。IMI越大,变量间的共同信息越多,相关性越强,反之,IMI越接近0,变量间的共同信息越少,相关性越弱。对于信号的第i个IMF分量ci(t)与原始信号x(t),它们之间的IMI定义为

(2)

式中:p(ci)和p(x)分别是第i个IMF分量ci(t)与原始信号x(t)的边缘概率分布;p(ci,x)是第i个IMF分量ci(t)与原始信号x(t)的联合概率分布。其中I(ci;x)的值越大,IMF分量与原始信号相关程度越强,反之,则相关程度越弱。

2.4 基于改进的HHT方法的特征提取算法

本文采用改进的HHT方法进行特征提取,算法的流程图如图3所示。算法的输入是采集的音频信号,输出是信号的特征向量。采用各个IMF分量与原信号的IMI作为评估IMF分量有效性的指标。计算IMI之前,分别对IMF分量和原始信号做了归一化处理,此时IMI的取值范围为[0,1],筛选条件设置为IMI的值大于0.1,满足筛选条件的IMF分量是有效的,即真实IMF分量。采用综合分类性能指标F作为特征提取的评估指标。

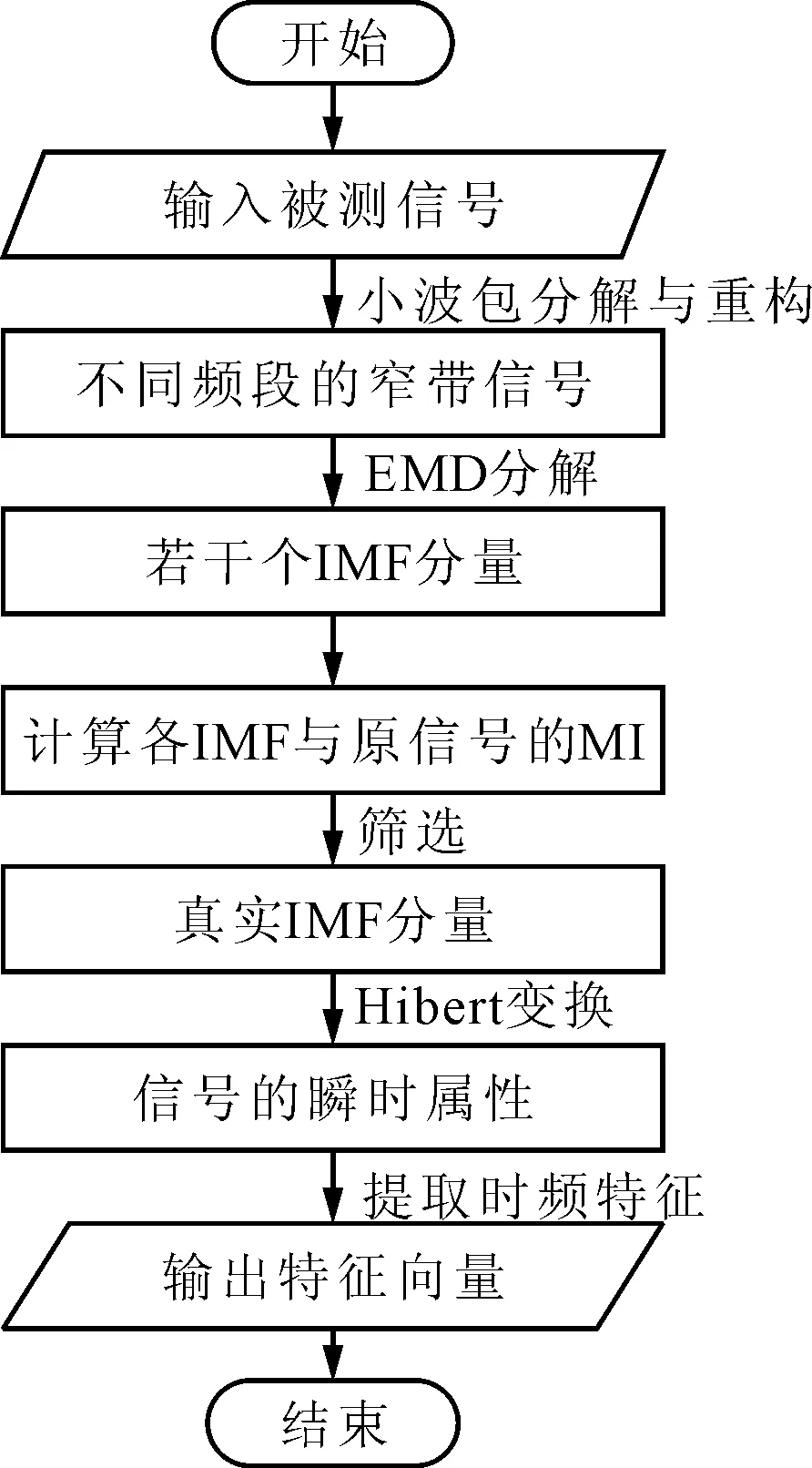
图3 改进的HHT方法特征提取算法流程图

本文算法的具体步骤如下。

步骤1小波包分解与重构。采用db6小波对信号进行3层小波包分解与重构,得到8个不同频段的窄带信号。

步骤2EMD分解。对每个窄带信号做EMD分解得到若干个IMF分量,具体实现如下:

(1)对于窄带信号x(t),找出信号的所有局部极大值、极小值点;

(2)对这些极值点进行样条插值,得到由所有局部极大值点构成的上包络线和所有局部极小值点构成的下包络线,分别记为u(t)、v(t);

(3)上下包络线的均值为

(3)

(4)令h(t)=x(t)-m(t),验证h(t)是否满足IMF分量的条件,若满足,则h(t)为第一个IMF分量;如不满足,以h(t)为输入继续进行前面的步骤,直至得到第一个IMF分量,并将其记为c1(t);

(5)将r1(t)=x(t)-c1(t)作为新的分析信号,重复步骤(1)到步骤(4),得到c2(t),此时记r2(t)=r1(t)-c2(t),重复上述步骤直到得到余项rm(t)是一个单调信号或者其值小于某个预先给定的阈值,分解结束。

步骤3筛选IMF分量。对原始信号和各个IMF分量做归一化处理后,计算各IMF分量与原始信号间的IMI。根据IMI的筛选指标选出能够反映信号特征的真实IMF分量,将筛选出来的真实IMF分量按照频率由高到低的顺序排序。

步骤4Hilbert变换。分别对步骤3得到的真实IMF分量做Hilbert变换,得到信号的瞬时属性,如瞬时频率、瞬时幅度、边际谱和Hilbert谱等;

步骤5提取时频特征,根据信号的瞬时属性,提取时频统计特征,如第一个IMF分量的瞬时幅度的均值、边际谱的带宽、边际谱的峰值、边际谱方差等。

虽然HHT方法具有很强的时频局部化能力,但是其存在的模态混叠和虚假IMF分量等问题会严重影响其精度。本文采用了小波包分解和基于IMI的IMF分量筛选方法改进HHT方法,提高了时频分析的精确度,从而更有效提取特征。本算法提供的更精确的时频分析,有利于进一步高效地提取信号中损伤信息。通过实验获得的有效时频特征有:边际谱的第一个峰值、边际谱第一个峰值对应的位置,边际谱方差,边际谱的带宽、边际谱的截止频率和第一个分量的瞬时幅度的均值等。与常规特征相比,采用改进HHT方法方法提取的特征的有效性更高。特征与类别标签的IMI反映它们之间的相关性,而特征与类别标签的相关性反映了特征对类别区分能力,因此特征与类别标签的IMI常用于衡量特征的有效性[17],IMI越大,对应特征就越有效。采用有损伤和无损伤各600个的测试样本,分别从改进HHT方法提取的特征与常规特征中选取有效性最好的5个特征进行对比,结果如图4所示。由图4可知:改进HHT方法提取的特征有效性最好的5个特征依次是边际谱的第一个峰值、边际谱的第2个峰值、边际谱第一个峰值对应的位置、边际谱的带宽和第一个分量的瞬时幅度的均值;常规特征中有效性最好的5个特征依次是信号的峰值因子、信号的均方根值、自相关函数的峰值、短时能量和信号的第5个频谱峰值。

图4 改进HHT方法提取的特征与常规特征对比图

由图4可知,改进HHT方法提取特征与类别标签的IMI整体上大于常规特征与类别标签的IMI,尤其体现在前3个特征,改进的HHT方法提取的前3个特征比常规特征更有效。虽然后面的特征略低于常规特征,但是改进HHT方法较大程度上提升了音频信号特征有效性的上限。图4表明,相比于常规特征,改进HHT方法提取的特征更有效,且具有更强的分类显著性,这些特征能够有效地表征损伤信息,可用于建立高效的损伤检测模型。

3 实验设计与分析

为了验证特征提取算法的有效性,本文采用敲击玻璃瓶产生的音频信号作为实验数据,通过对音频信号的时频分析,提取相关特征,进行损伤检测。音频信号采集频率为48 kHz,采样点数为2 048。在损伤检测之前,需要对信号进行特征提取,选择一部分有效的特征集来表征信号存在的损伤信息。然后,采用3层BP神经网络来检查特征的有效性。神经网络的输入是特征集,输入层的节点数是特征集的维数M。根据经验,隐藏层的节点数被设置为2M+1较为合适。由于本文讨论的是二分类问题,所以输出层只需要一个节点,输出结果为0或1,0代表无损伤,1代表有损伤。此外,由于本文实验数据规模相对较大,为了保证网络精度和收敛速度,选择Levenberg-Marquardt函数作为神经网络的训练函数[18],设定BP神经网络的学习速率为0.1,停止条件为最大训练次数为1 000次,或者验证集的出错样本数达到10个,或者平方误差的变化率小于给定值。

本文采用精确率、召回率以及综合分类性能指标F来评价实验结果。a表示被正确判定出来的正类数,b表示将正类错误判定为负类数,c表示将负类判定为正类数,d表示被正确判定出来的负类数。计算基于二分类问题的混淆矩阵,具体的评价参数如表1所示。

表1 二分类问题的混淆矩阵

由于损伤检测的目的是检测出信号中的损伤信息,故设有损伤为正类,无损伤为负类。精确率P为正确检测出损伤占所有检测为损伤的比例,也就是查准率;召回率R为正确检测出损伤占所有损伤的比例,也就是查全率;F值是精确率和召回率的加权调和平均,是分类模型中常用的评价指标。

精确率、召回率和综合分类性能指标F的计算公式如下

(4)

(5)

(6)

在MATLAB平台上运行神经网络,实现对敲击信号的分类,检测该信号对应的玻璃瓶是否存在损伤。实验中选取2 000个样本信号,包括1 000个无损伤和1 000个有损伤的敲击信号,这些信号分为1 200个样本的训练集和800个样本的测试集。为了验证上述理论,设计了3组实验来验证改进HHT方法的参数设置的有效性。第1组实验,采用db4小波对信号进行4层小波包分解与重构,然后基于不同的IMF分量筛选条件,进行改进HHT方法的性能测试,实验结果如表2所示。第2组实验,采用db4小波对信号分别进行2、3和4层小波包分解与重构,然后基于IMI>0.1的IMF分量筛选条件,进行改进HHT方法的性能测试实验结果如表3所示。第3组实验,分别采用db4、db6、db7和db8小波对信号进行3层小波包分解与重构,然后基于IMI>0.1的IMF分量筛选条件,进行改进HHT方法的性能测试实验结果如表4所示。同时,为了验证本文提出算法的有效性,分别采用常规方法、原始HHT方法和改进HHT方法进行特征提取,测试不同方法的性能实验结果如表5所示。由表2可知,在小波基均为db4和分解层数均为4的情况下,基于能量比值法的IMF分量筛选效果最差,效果甚至差于未进行IMF分量筛选,而其他3种筛选效果均优于未进行IMF分量筛选,相关系数法和互信息量法效果相近,IMI指标略优于其他两种,其综合分类性能指标F达到92.22%。由此可知,有效的IMF分量筛选能够在一定程度上解决了虚假IMF分量造成的误差。由表3可知,在小波基为db4和IMF分量筛选条件为IMI>0.1的相同情况下,分解层数为3时提取的特征最有效,其综合分类性能F达到93.34%。由表4可知,在分解层数为3和筛选条件为IMI>0.1的相同情况下,db4、db6、db7和db8这4种小波的效果相近,其中db6略好于其他小波,此时的分类性能最好,其平均精确率可达96.13%,召回率为93.25%,综合分类性能指标F达到94.67%。由表5可知:相同数量的常规特征的平均精确率为86.59%,召回率为85.75%,综合分类性能指标F为86.16%,性能低于HHT方法提取的特征,这验证了本文改进的HHT方法提取特征相比于常规特征具有的优势性;原始的HHT方法提取相同特征的平均精确率为90.69%,召回率为85.23%,综合分类性能指标F为87.86%;改进的HHT方法提取的特征的分类性能远高于原始的HHT方法,相比之下综合性能提高了7.7%。这说明改进的HHT方法能够有效提取音频信号中的损伤信息,验证了本文方法的有效性。

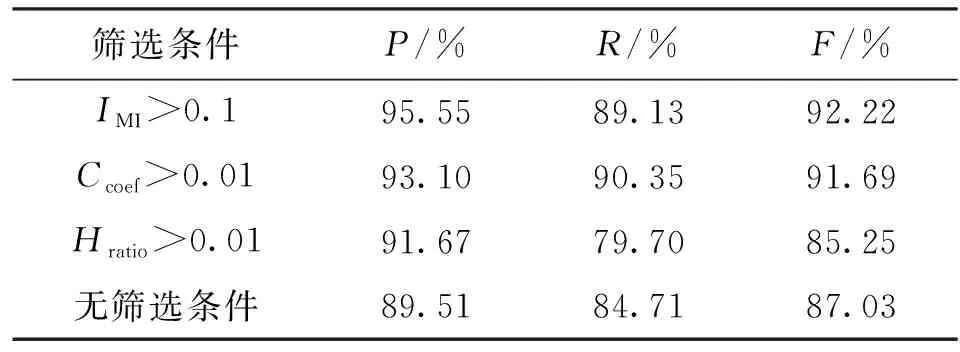
表2 不同筛选条件的改进HHT方法性能

注:IMI表示IMF分量与原始信号间的互信息量;Ccoef表示IMF分量与原始信号间的互相关系数;Hratio表示IMF分量与原始信号间的能量比值。

表3 不同小波包分解层数的改进HHT方法性能

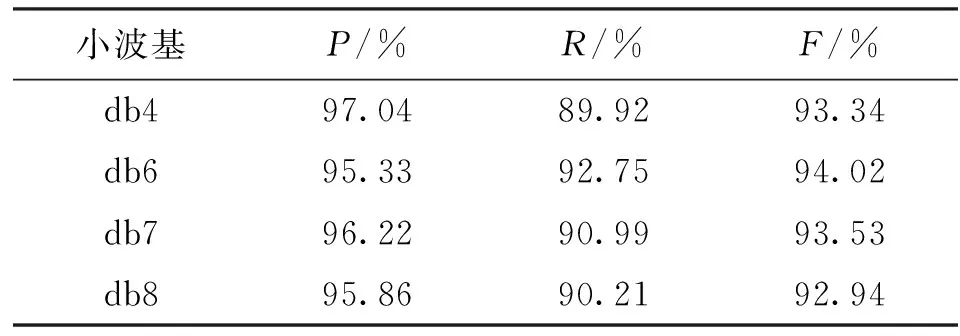
表4 不同小波基的改进HHT方法性能

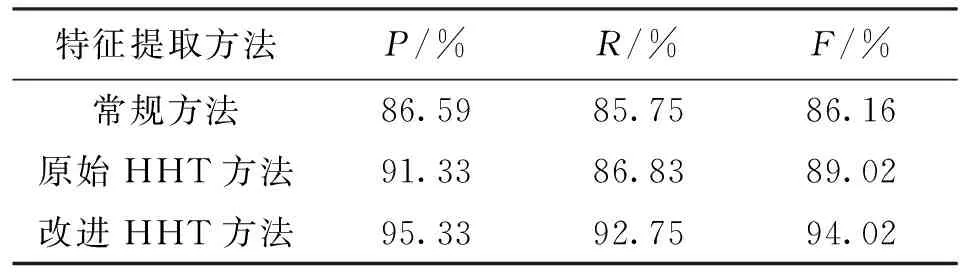
表5 常规方法、原始HHT方法和改进HHT方法性能比较

注:改进HHT方法采用本文讨论的参数设置,即小波基为db4,分解层数为3,筛选条件为IMI>0.1。

4 结 论

本文提出了一种采用改进HHT方法的音频特征提取方法。首先采用db6小波对信号做3层小波包分解与重构预处理得到一系列窄带信号,再对窄带信号做EMD分解,然后基于IMI剔除虚假IMF分量,最后进行Hilbert变换提取相关时频特征。将这些特征作为BP神经网络的输入,利用神经网络的非线性映射对损伤样本进行自动识别。经实验验证,本文方法的平均综合分类性能指标F为94.67%,能够较准确地区分损伤样本和无损伤样本。对于不确定待测信号频段的情况,选取小波基和分解层数时,可以通过对比实验分别从Daubechies小波族、Coiflets小波族和Symlets小波族中选取最佳的小波基,通过对信号进行2到6级的小波包分解选取最佳分解层数。

本文方法不仅改善了经验模式分解过程中产生的模态混叠,同时也在一定程度上解决了虚假IMF分量造成的误差,提高了时频分析的精确性,最终提高了损伤检测的准确率和稳定性。

本文改进的HHT方法在分析非平稳非线性信号方面具有一定的优势和有效性,可用于结构健康监测、齿轮故障振动诊断和信号滤波等领域的信号分析,有利于从非平稳非线性的信号中挖掘出隐含的信息,增加信号分析的准确性。