基于单目AR环境下的目标识别与跟踪算法

郭阳阳，孙 涵

(南京航空航天大学 计算机科学与技术学院，江苏 南京 211106)

0 引 言

增强现实技术(augmented reality，AR)是一种把原本在现实世界的一定时间空间范围内很难体验到的实体信息(如视觉信息、声音、味道、触觉等)，通过科学技术模拟仿真后再叠加到现实世界被人类感官所感知，从而达到超越现实的感官体验的技术。这种技术的目标是在屏幕上把虚拟世界套在现实世界并进行互动。

增强现实技术的应用可以给人们的生活带来很多便利，比如在城市规划以及房产开发中，开发者可以使用增强显示技术模拟城市开发以及房屋建造的过程，有利于设计与管理人员对各种规划方案进行辅助设计与方案评审，规避设计风险。同样，增强现实技术也可以给人们的生活带来很多乐趣，如Pokemon Go就是一款利用增强现实技术设计而成的游戏。

三维配准[1-3]是增强现实技术中的最核心技术。在增强现实技术中配准的目的是对影像数据进行几何上的精确理解。这样，要叠加的数据的定位问题就成了增强现实技术中最关键的问题。其中，数据的定位可以用旋转平移矩阵来表示，而求取旋转平移矩阵就是文中要研究的主要内容。

流程如图1所示。

图1 流程图

1 相关工作

1.1 李群与李代数

AR是一种基于3D模型的技术，文中采用的图片位置的表示方法为旋转矩阵和平移矩阵，因此主要介绍三维欧氏群SE(3)以及对应的李代数se(3)。

SO(3),t∈R3}

(1)

其中，R为旋转矩阵；t为平移矩阵；SO(3)为三维旋转群。

R满足属性RRT=I，I为单位矩阵。将R看作一个随时间变化的函数，即R(t),有R(t)R(t)T=I，对等式两边求导得：

R(t)'R(t)T+R(t)TR(t)'=0

(2)

于是：

R(t)'R(t)T=-(R(t)'R(t)T)T

(3)

可以看出，R(t)'R(t)T是一个反对称矩阵。对任意一个3×3反对称矩阵A，存在一个向量a=[a1,a2,a3]T，满足Ab=a×b，其中b为任意三维向量，所以有：

(4)

由此可得：

(5)

将SO(3)的结论推广到SE(3)，由于SE(3)多了平移的三个自由度，因此，使用p=[p1,p2,p3]来表示平移。

由此可以得到：

(6)

根据矩阵的指数映射，使用θ和α表示向量a的模长和方向，可以得到：

exp(θα)=cosθI+(1-cosθ)aaT+

sinθA

(7)

(8)

最终得到：

(9)

1.2 迭代最近邻点(iterative closest points，ICP)算法

在单目AR的图像跟踪中，每一帧都需要计算相对于模板图片的旋转平移矩阵。假设已知模板图片以及当前帧两组匹配的特征点，就可以利用1.1节中的相关知识求出旋转平移矩阵。

视频的每一帧随时间变化而变化，因此，可以将视频看作一个随时间变化的函数，这就满足了李群与李代数的基本条件。下面构造矩阵T。由于每次运算是以前一帧的矩阵为初始矩阵，所以矩阵初始化在模板图像识别过程实现，实验中，将R矩阵初始化为单位矩阵，t矩阵元素全为0，经过多次迭代得到最终矩阵。

假设a为模板图像特征点坐标，b1为当前帧特征点坐标，b2为上一帧特征点坐标(a、b1、b2都为齐次坐标)，对视频函数求导得：

(10)

对式10变形得：

Gh=b1-b2

(11)

其中：

(12)

h=(a1,a2,a3,p1,p2,p3)T

(13)

由于h有6个参数，G只有3行，3个方程不能求得6个未知数，所以需要有多个点参与，最后求得h如下：

h=(GTG)-1GT(b1-b2)

(14)

求得h后，根据式7～9，即可求出最后的旋转平移矩阵T。

2 目标图像识别

在目标跟踪问题中，目标识别是目标跟踪的前提。文中使用的模板目标图片如图2所示。

图2 模板图片

识别过程如下所述。

2.1 提取图像FREAK特征

常见的图像特征描述子有SIFT[4]、SURF[5]、ORB以及HOG特征等，但是这些特征描述子有的提取速度慢，有的局限性大，而图像识别与跟踪对实时性要求很高，因此这些特征描述子都不能满足要求。FREAK[6]特征也许精度不如SIFT以及SURF，但是其提取速度快，可以满足实时性的要求；而对于FREAK特征精度的问题，可以对FREAK特征进行多次优化，以保证最后得到的匹配点的正确性。

2.2 基于单应性矩阵的特征点匹配结果提纯

在提取出模板以及视频当前帧的FREAK特征后，可以得到两组匹配的特征点，为保证匹配特征点的精确度，要将其中一些匹配错误的特征点去掉。具体过程如下：

(1)Hough投票[7-8]。每个特征点的信息中都包含坐标、旋转角度以及尺度的四维信息，利用这四维信息对每个特征点进行投票，选择得票最多的bin上的特征点。

(2)计算单应性矩阵[9]。单应性矩阵为一个3×3的矩阵，表示为：

(15)

矩阵H会将一幅图像上的点的坐标a=(x1,y1,1)映射到另一幅图像上的点的坐标b=(x2,y2,1)。因为图像坐标的Z值都为1，所以由H和cH所得到的b的坐标是一样的，其中c为常数。因此，将h33固定为1，这样H就还有8个自由度，根据每组点对，可以得到2个方程，如下：

(16)

(17)

所以总共需要4组点对来求得H。式16、17经过变换后，可以写成一个矩阵A与一个向量h相乘的形式，如下：

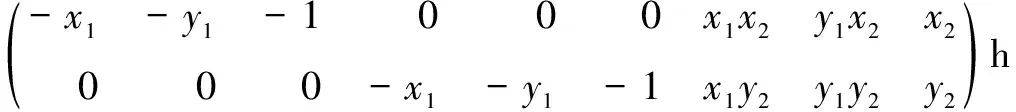
(18)

其中

h=(h11,h12,h13,h21,h22,h23,h31,h32,h33)T

(19)

因为有4组点对，每个点对可以写成2×9的矩阵，所以可以构造出一个8×9的矩阵。矩阵构造完成后，要对Ah=0进行求解，然后对A进行SVD分解，即：

A=U*Σ*VT

(20)

则V的最后一列即为所求的h，将h变形成3×3矩阵，即为H。

(3)选择最优单应性矩阵。在步骤1中求得多组匹配的特征点，而求解单应性矩阵只需要四组匹配的特征点，因此，可以多次求解单应性矩阵，然后寻找其中的最优解。

首先，要确定两组点的对应关系是否一致，例如：在模板图像中的四个点可以按照顺时针方向连接起来，则视频帧中对应的点也要能够按照顺时针方向连接起来，如果不能，就要重新选取四个点；经过多次上述步骤后，可以得到多个单应性矩阵，然后将所有点对代入到每个单应性矩阵中，计算每个单应性矩阵的误差和，选择误差最小的单应性矩阵作为最优解。

(4)判断所求的单应性矩阵是否满足条件。将所有匹配的特征点对代入到单应性矩阵中，设定一个误差阈值，计算点对中误差小于阈值的数量，如果数量大于一定值，则将这些特征点对记录下来，作为提纯后的特征点来计算旋转平移矩阵。

2.3 求解初始旋转平移矩阵

经过特征点的匹配及一系列优化过程，得到了模板图片与视频中图片的两组匹配的特征点对，利用ICP[10]算法可以求得初始的旋转平移矩阵。

3 目标图像跟踪

在第二节得到了模板图像所在的第一帧图像，以及初始的旋转平移矩阵，本节将要就模板图片的跟踪以及求解每一帧的旋转平移矩阵展开讨论。

模板图片跟踪的实时性要求比识别高，所以就不能使用提取特征点再匹配这样耗时比较高的方法，然而在跟踪过程中，视频前后两帧模板目标图片所在的位置并不会发生太大的变化，因此，可以使用模板匹配的方法，在上一帧特征点坐标的周围找到当前帧特征点的坐标；由1.1节介绍的李群与李代数内容，可以使用六个自由度的矩阵的导数来求出旋转平移矩阵，而视频流可以看作一个随时间变化的连续函数，连续两帧的坐标差可以看作是函数的导数。有了上面这些理论后，就可以利用上一帧求得的特征点坐标以及旋转平移矩阵来求得当前帧的特征点以及旋转平移矩阵。算法的具体过程如下所述。

3.1 目标图像特征点选择

为了让特征点尽量分散以及保证特征点的稳定性，选择以下类型的特征点，如图3所示(其中圆形特征点为(1)～(4)所选择的特征点，菱形特征点为(5)选择的特征点)。

图3 特征点选取

(1)选择特征点中距离所有特征点的中心点最远的点；

(2)选择距离(1)中选择的特征点最远的特征点；

(3)选择距离(1)和(2)选择的特征点所连成的直线距离最远的特征点；

(4)选择与(1)、(2)和(3)选择的特征点所围成的四边形面积最大的特征点；

(5)选择图像上一帧所使用的特征点。

3.2 特征点模板匹配

在上一帧中，已经得到了所需要的特征点位置，那么在当前帧中得到对应的特征点的位置就成了关键性的问题。由于前后两帧特征点的位置变动不会很大，因此，文中使用模板匹配[11-12]的方法，在上一帧特征点的周围匹配当前帧的特征点。具体过程如下：

(1)选定特征点模板：在模板图片中，以特征点位置为中心，截取一个12×12(见图3)的patch，以这个patch作为当前特征点模板。

(2)划定当前帧特征点位置范围：由于前后两帧特征点位置不会变化很大，因此，以上一帧特征点位置为中心，在当前帧中截取一个36×36的patch，作为当前帧特征点的范围。

(3)确定特征点位置大概范围[13]：特征点的位置在36×36的小patch中，但是如果对36×36的每一个点都进行模板匹配，这样效率无疑会很低，因此，可以选取一个特定步长，先大致确定特征点的范围，以提升效率。在36×36的范围内，以3为步长，比较以当前点为中心截取的12×12的patch与模板patch的差异，选出两个差异最小的点。选取两个差异最小的点，是为了保证得到的结果是全局最小，而不是局部最小。

(4)确定特征点位置：在步骤3中，得到了两个5×5的特征点范围，对这两个5×5的patch中的每一个点与模板patch进行模板匹配，选取差异最小的一个点作为特征点位置。

由于确定每个特征点位置的过程是独立的，因此可以使用多线程来进行加速，进一步提高算法运行速度。

3.3 当前帧旋转平移矩阵计算

在3.2节中，计算出了与模板图片特征点对应的当前帧中特征点的位置，这样就得到了两组匹配的特征点[14]，可以使用1.2节中的ICP算法进行求解。在ICP算法中，以上一帧旋转平移矩阵为初始矩阵，两帧之间特征点位置的差作为导数，ICP算法的条件得以满足，可以求得当前帧的旋转平移矩阵。然后将当前帧作为上一帧，迭代求出每一帧的旋转平移矩阵。

4 实验结果

实验运行环境为Windows10，处理器频率为3.60 GHz，镜头分辨率设为480×360。实验中图片识别和图片跟踪在两个线程下进行，其中，图片识别的过程在60 ms左右，图片跟踪如果在单线程下运行，每一帧的跟踪时间大概为20 ms左右，如果模板匹配过程在多线程下运行，跟踪速度明显加快。实验效果如图4所示。

首先对目标图片识别过程进行时间复杂度分析。在特征点匹配过程中使用了暴力匹配的方法，则匹配过程时间复杂度为O(n2)；求解单应性矩阵每4个特征点为一组，求解出n个单应性矩阵，则时间复杂度为O(kn)；求解出单应性矩阵后，每个特征点都与多个单应性矩阵计算误差，则时间复杂度为O(kn)；ICP算法过程中，选出的n特征点迭代地更新矩阵，直至收敛，则时间复杂度为O(kn)。

图4 图片识别与跟踪效果图

目标图片跟踪过程的时间复杂度为：特征点选择过程时间复杂度为O(n)；特征点模板匹配过程中，n个特征点中的每个点都要与patch中的k个点进行模板匹配，则时间复杂度为O(kn)。

5 结束语

文中提出了一种基于单目AR[15]的图像检测及跟踪算法。该算法首先对模板图像提取FREAK特征，然后在视频的每一帧中提取FREAK特征与模板图像特征进行比较，通过Hough投票、计算单应性矩阵等过程优化特征点的匹配结果，利用ICP算法求得图像的初始旋转平移矩阵，完成检测过程；对于图像的跟踪过程，利用视频上一帧中使用的特征点，通过模板匹配求得本帧中对应特征点的位置，然后利用ICP算法迭代求出视频每一帧的旋转平移矩阵。实验结果表明，该算法能够快速对目标图片进行识别并且能够实时跟踪目标图片的位置，对于AR中目标图片的识别与跟踪具有重要意义。