基于坐标变换的交互多模型车载定位研究*

焦雨琪,牛 蕊,夏 志

(南京邮电大学 通信与信息工程学院，江苏 南京 210003)

0 引言

随着汽车的使用量增多以及道路越来越复杂，人们对于车辆定位导航精度的要求也越来越高[1]。如今二维平面的车辆导航可以满足基本的定位需求，但是三维平面内的定位精度还不够，尤其是高度定位，在遇到复杂的三维场景时，经常不能判断车辆在哪一层，从而出现导航信息匹配实际路线错误的现象[2]。为了提高车辆的定位精度，考虑对GPS数据进行滤波处理[3]，在现实条件下，实际的系统总是非线性的，此时对比标准卡尔曼滤波，无迹卡尔曼滤波更能表现出其优越性。为了解决车辆运动状态突然变化时定位效果不佳的现象，采用交互多模型算法，使其具有自适应滤波功能。坐标变换算法将建立平面和斜坡两个不同的坐标系，通过两个坐标系X、Y、Z三轴之间的联系求出平面坐标系中车辆的高度数据。

1 无迹卡尔曼滤波

卡尔曼滤波是一种动态估计算法，通过状态方程和观测方程实现“观测-更新”这一动态传递过程[4]。

考虑如下的非线性系统：

Xk=f(Xk-1,k-1)+Γ(Xk-1,k-1)Wk-1

(1)

Zk=h(Xk,k)+Vk

(2)

其中，Xk是系统的状态向量；f(·)是非线性的过程函数；Zk是观测向量；h(·)是观测的非线性函数；Wk-1、Vk是零均值白噪声序列。

无迹卡尔曼滤波首先对该系统状态向量进行U变换，再对变换后的状态向量进行滤波处理[5]。过程如下：

(1)计算Sigma点：

(3)

其中 ，n为状态向量维数，Pk-1为误差协方差矩阵。

(2)将Sigma点经过f(·)和h(·)非线性变换后再求和可以得到状态更新量和观测更新量Xk,k-1和Zk,k-1。

需要注意，U变换只是选取少量确定的Sigma点，不是随机地从给定分布中进行采样。

2 交互多模型

在现实生活中运动目标往往是机动的，单凭一种运动模型远远不能描述车辆的运动状态[6]。在目标跟踪的过程中采用多个运动模型，各个模型之间的转移服从马尔可夫链。

车辆的运动模型分为两大类：CV模型和CA模型。CV模型描述的是速度不变的直线运动，此时只需要考虑车辆的位置和速度。CA模型描述的是车辆加速度不变的直线运动，此时需要考虑车辆的位置、速度和加速度[7]。

CV模型的状态向量可为:

CA模型的状态向量可为:

其中，XX、XY、XZ分别为X轴、Y轴、Z轴的位置信息，VX、VY、VZ分别为X轴、Y轴、Z轴的速度信息，AX、AY、AZ分别为X轴、Y轴、Z轴的加速度信息。

观测向量为：

其中，Sx表示X轴方向的位置信息，Sy表示Y轴方向的位置信息，Sz表示Z轴方向的位置信息，ΔS表示测量时间内车辆位移的路程信息。以上信息可由GPS信息和里程计信息获得。一般来说，观测向量维数必须小于或等于状态向量的维数。

3 交互多模型卡尔曼滤波

交互多模型使用不同的模型对应不同的运动状态，首先输入交互，在各个模型切换时通过转移概率来控制，每个模型并行滤波，再融合各个模型的概率输出最终的状态估计[8]。

3.1 输入交互

假设模型i到模型j的转移概率为Pij，每个滤波器的模型概率为μj(k-1)。

模型i到j的混合概率为：

(4)

其中归一化常数：

(5)

模型j的混合状态估计：

(6)

模型j的混合协方差估计：

(7)

将混合状态估计作为滤波输入的初始状态。

3.2 并行滤波

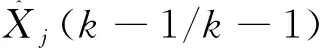
量测更新得到k时刻的状态值和协方差矩阵：

(8)

(9)

(10)

其中，Z(k)为观测量。

3.3 更新概率模型

模型j的似然函数：

(11)

其中：

vj=Z(k)-Zj(k/k-1)

(12)

(13)

更新后模型j的概率为：

(14)

其中，c为归一化常数：

(15)

3.4 输出交互

最终k时刻的总状态估计：

(16)

k时刻总的协方差估计：

(17)

从以上步骤可以看出滤波的结果是多个模型加权后的模型，不同时刻选取概率最大的模型来描述此时的运动状态。

4 坐标变换

车辆在平地上是二维空间，到了坡面，对于全局坐标来说还是三维，但是对于坡面坐标系来说就是二维，高度为零[9]。坐标变换是对空间实体的位置描述，是从一种坐标系变换到另一种坐标系，通过两个坐标系之间的对应关系来实现。任何维的旋转可以表述为向量与合适尺寸的方阵的乘积。最终一个旋转等价于在另一个不同坐标系下对点位置的重新表述[10]，如图1所示。

图1 坐标系S和坐标系S1示意图

如图1坐标系S、S1所示，φ为方向角，θ为仰角，取坐标系S为全局直角坐标系，r=xex+yey+zez为S1坐标系上某个动点坐标值。

令rd1=xd1ex+yd1ey+zd1ez为平面M1上的已知点，该平面法向矢量设为n1=cosθsinφex-cosθcosφey+sinθez，其中ex、ey、ez为S坐标系的坐标轴单位矢量。则M1平面上与S坐标原点最小距离为n1·rd1，该点称为ro1点，平面方程为(r-rd1)·n1。

取坐标系S1的原点为ro1=(n1·rd1)n1，坐标轴Z1取为平面法向量n1，X1轴和Y1轴在M1平面上。用S1表示的动点rs1与S表示的r的关系为r=ro1+rs1。

取X1轴为M1平面上的方位方向，Y1轴为仰角方向，则ez1=n1,ex1=(cosφ,sinφ,0)，又因为ey1·ex1=0，ey1·ez1=0,故得:

ey1=(-sinθsinφ,sinθcosφ,cosθ)

(18)

(19)

当φ=0°时，

(20)

显然，z1=0即为S1坐标系的M1平面方程。由于x、y可由GPS得到，z1又为0，自然可以求出高度值z[11]。当高度位置信息求出之后，可以利用GIS定位到确定的一条车道上，避免出现车辆定位错误的现象[12]。

5 仿真实验及结果分析

仿真实验时，车辆在三维空间内做S型运动，方向角45°，坡度45°，初始位置位于(100,500,0)坐标处，初始速度为(0,10,0)，经过直线匀速运动250滤波点之后，开始上坡进行变速S型运动。采样周期为0.1 s[13]。图2～图4为仿真结果图。

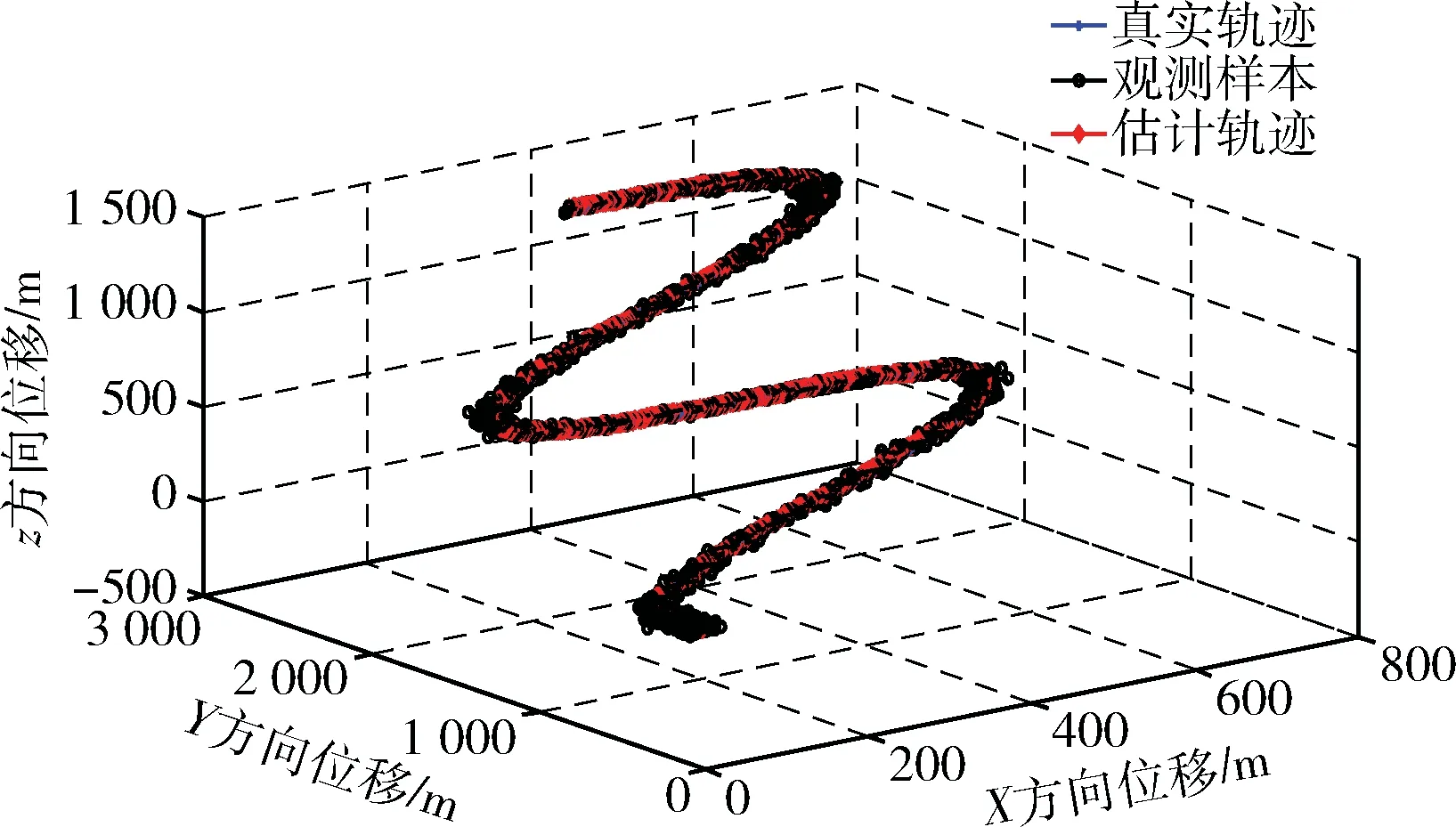
图2 基于坐标变换的IMMUKF车辆运动轨迹

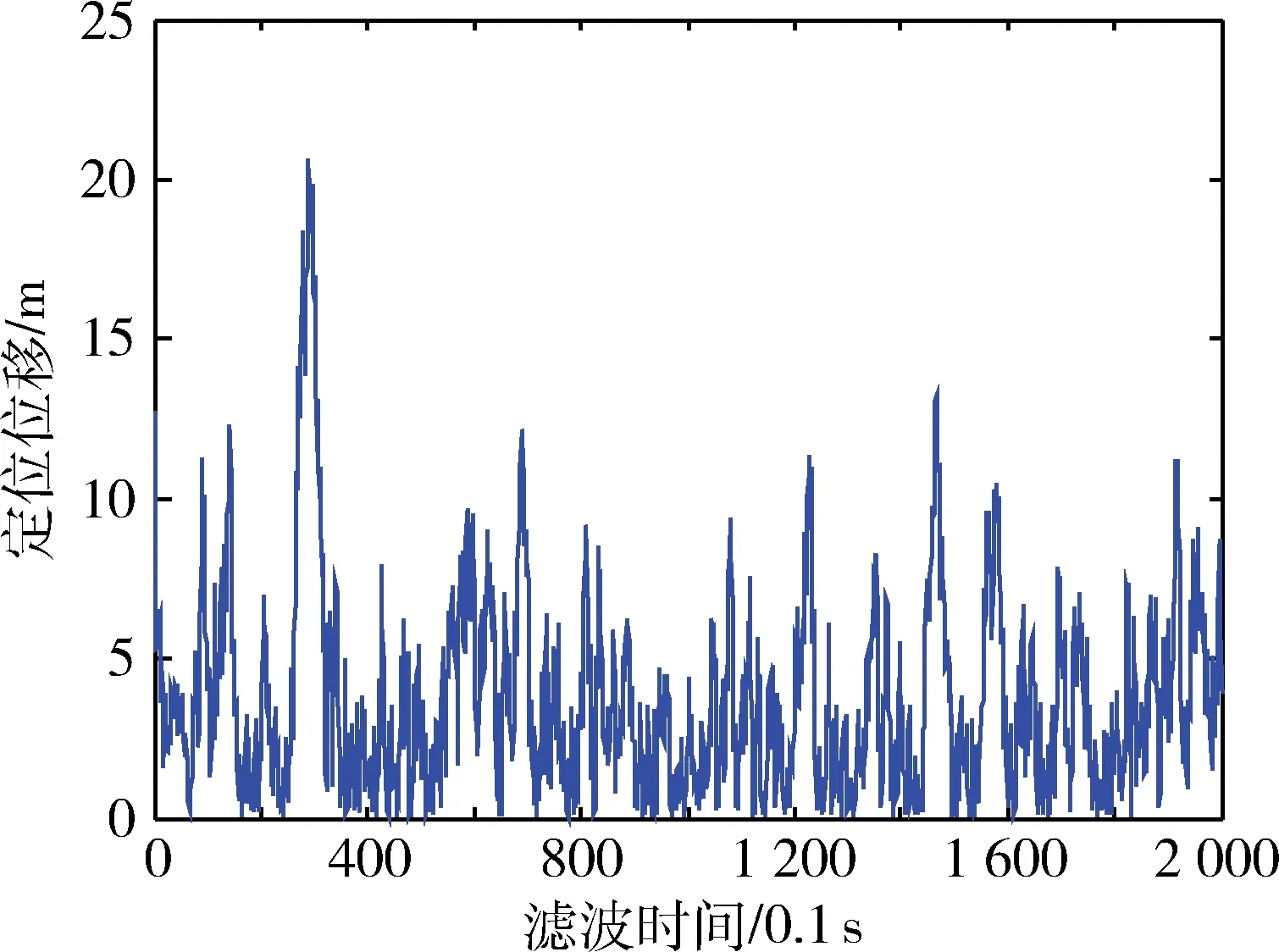
图3 基于IMMUKF-3D算法车辆运动Z轴方向定位误差

图4 基于坐标变换的IMMUKF车辆运动Z轴方向定位误差

表1和表2列出了4次仿真实验中高度误差和总误差数据。

表1 车载三维S型运动高度定位误差 (m)

表2 车载三维S型运动定位总误差 (m)

此实验由IMMUKF-3D算法和基于坐标变换的IMMUKF算法分别模拟三维空间内车辆上坡运动。由仿真实验结果图2可以看出车辆在斜坡上做S型拐弯运动，初始位于(100,500,0)坐标处，初始速度为(0,10,0)，经过直线匀速运动250滤波点之后，开始上坡。采用交互多模型融合无迹卡尔曼滤波，在车辆运动状态出现突然加速或突然减速时能够及时调整模型概率，使车辆运动速度能够很好地追踪上标准速度。由图3、图4可以看出，基于IMMUKF-3D算法车辆运动Z轴方向定位误差与基于坐标变换的IMMUKF车辆运动Z轴方向定位误差相比，明显误差较大。图4由于前250滤波点时还在平地，坐标还未变换，因此无高度误差。通过表1和表2进一步分析仿真实验结果可以更加直观地发现，基于坐标变换的IMMUKF算法在高度定位精度和总体定位精度方面都有明显的提高。其能够区分车辆是在桥上还是桥下，减少由于高度定位误差较大而将车辆导航地图匹配出错的情况[14]。

从仿真结果可以发现基于坐标变换的IMMUKF算法在三维空间中可以有效减少高度定位误差，在车辆上坡的情况下可以减少车道匹配出错的情况，在一定程度上有效地提高了车辆的定位精度。

6 结束语

由于GPS提供的高度信息相比水平信息具有更高的误差，利用之前的IMMUKF-3D算法并不能完全解决高度定位精度不够的问题，导致车辆导航错误[15]。利用坐标变换的原理，将三维空间转化为坡面二维平面，通过三维坐标系的X轴、Y轴、Z轴与二维平面的X1轴、Y1轴之间的关系求出车辆高度信息。通过仿真实验结果可以直观发现，基于坐标变换的IMMUKF算法在高度定位精度和总体定位精度方面都有明显的提高。