车头长度对高速列车气动特性与声场特性影响的数值分析及降噪研究
2018-10-13刘晓日罗江泽
刘晓日,罗江泽,赵 哲,黎 苏,李 扬
(河北工业大学 能源与环境工程学院,天津 300401)
随着社会的发展,高速列车越来越多地出现在人们的生活中,因其高速特性,乘坐高铁出行极大地缩短了人们的乘车时间。但诸多因素阻碍了高速列车的进一步发展,最突出的问题便是其高速行驶时巨大的行车阻力对电力资源极大的需求以及噪声对人们正常生活的影响,因此降低高速列车的行车阻力和噪声近年来成为人们研究的热点[1]。列车的气动阻力与速度的平方成正比,随着列车速度的提高,气动阻力在总阻力中所占比例逐渐增加,列车速度超过一定值时,气动阻力成为高速列车的主要阻力[2]。通过高速列车气动优化设计能够有效降低气动阻力、提高高速列车的气动性能[3]。对于时速为250~300 km·h-1的高速列车来说,总阻力的75%~80%起因于外部气动阻力[4]。高速列车的头部对周围空气流场具有决定性的影响,从列车头部着手改善车体外形是研究的重点[5]。当列车的运行速度达到300 km·h-1,列车运行所产生的气动噪声将会超过轮轨噪声,成为高速列车的主要噪声[6]。文献[4]将理论分析、实验研究、数值模拟相结合,对不同型号的高速列车各种行驶环境下的空气动力特性以及噪声源进行分析。文献[7]建立3种纵向剖面线和3种水平剖面线组合下的9种高速列车头型,研究了头部控制线形状对高速列车气动噪声的影响。文献[8]通过对铁路车辆噪声源机理和噪声源位置的分析,提出了降低噪声的方法。文献[9]研究了不同速度下高速列车周围流场的变化,得出气动噪声在很宽的频带内存在,是1种宽频噪声;控制列车运行过程中产生的脉动压力,能够减少气动噪声。文献[10]对4种不同头部外形高速列车的气动性能进行风洞试验研究,实验表明车头外形越细长,对减阻越有利。文献[11]对鼻尖高度、排障器前端伸缩量、转向架区域挡板倾角等关键设计变量进行了优化设计以及与气动阻力和气动噪声的相关性分析,在此基础上提出了综合性能较佳的新头型气动外形。文献[12]对高速列车的流线型头型进行多目标优化设计,优化后的列车气动阻力减小了4.15%。
本文应用等比例同距离方法对高速列车头部进行模型构建,将车头长度设置成模型变化的唯一参数,从理论上保证了模型的相似性。宽频噪声模型采用的RNG k-epsilon模型做定常计算,FW-H声学模型采用大涡模拟(LES)模型进行瞬态计算,同时对高速列车的表面压力、阻力、升力、气动噪声偶极子声源、远场气动噪声特性进行分析,并总结出这些参数随车头长度的变化规律,将同一速度、不同高速列车模型附近的脉动压力分布规律和远声场信息进行对比分析。
1 计算模型
1.1 理论基础
宽频噪声模型采用的RNG k-epsilon模型做定常计算,FW-H声学模型采用大涡模拟(LES)模型进行瞬态计算。
RNG k-epsilon方程为
Gk+Gb-ρε-YM+Sk
(1)
(2)
式中:GK表示由于平均速度梯度而产生的湍流动能;Gb表示由于浮力而产生的湍流动能;YM代表在可压缩湍流中波动膨胀的贡献对总耗散率的贡献;αK和αε分别表示k和ε的逆普朗得系数;Sk和Sε为自定义有源项。
大涡模拟(LES)控制方程为
(3)
(4)

对于高速列车气动噪声的研究,常采用莱特希尔(Lighthill)的理论,用单极子、偶极子和4极子声源来代表气动噪声源。单极子和偶极子声源分布于物体的表面,4极子声源分布于物体周围的流体空间。当分析问题时,因为将运动的固体视为刚体,所以忽略了单极子声源。Lighthill总结了流场中4极子和偶极子所产生的声强比为ΙQ/Ιd∝(Uo/ao)2H(R),其中的Uo为物体运动的速度,ao为当地声速。由此可得,气动噪声中4极子声源与偶极子声源强度之比正比于马赫数的平方。本文中设定高铁的运动速度约为0.285马赫,属于低马赫运动,其4极子源噪声强度远小于偶极子源,故4极子源也可忽略不计。流体对固体的脉动压力不能产生流体中的声波而是固体中的振动波,只有固体对流体的起伏力能导致声波的产生,高速列车的噪声源可简化成偶极子声源。在做这种简化时声源的尺寸应远小于其向外辐射声波的波长,而高速列车的长度大,所以在高速列车的表面分布有无穷多个偶极子声源。因此,了解高速列车表面的气动偶极子分布规律,是降低高速列车气动噪声的基础。
不同声源的声辐射场是不同的,而运动声源的声辐射场又不同于静止声源的声辐射场,流场中匀速运动固壁表面所诱发的气动偶极子声源的空间声辐射指向特性与诸多因素相关,譬如物体的运动速度、脉动压力的频率、偶极子的运动方向和观察者方向的夹角等。在实际的监测过程中还需考虑运动声源的多普勒效应,随着声源与接受者之间距离的缩短,收到的声波频率较高。综上所述,获得高速列车周围的声场信息是非常困难的[13],需要设置有限个监测点,通过这些点的变化情况来推测整个声场的变化[14]。
1.2 几何模型
在改变车头长度的同时车头曲面也会发生变化,保证不同长度的车头曲面的相似性是研究问题的基础。如图1所示,选定1条主轴线,主轴线起始于水平样条控制线和横向样条控制线的交点,沿水平方向终止于车身控制线所在的平面。主轴线的长度即表示车头的长度,使得生成车头曲面的控制线和主轴线通过若干条距离控制线(图中未标记线条均为距离控制线)相关联,即可在改变主轴线的同时使得头型控制线改变。按上述方法应用进行三维建模,在车头曲面生成过程中车头形状仅由水平、横向样条控制线和车身形状控制线决定。车头的长度由主轴线的长度确定,在生成5~13 m车头长度过程中仅通过改变主轴线的长度,便可得到不同的模型形状。车尾和车头长度是相同的。

图1 高速列车简化模型形状控制线
高速列车运行时通常为6~8节车厢,每节车厢的长度在24~27 m范围内,总长度超过200 m。中国还开始试验运行世界首列加长版16辆编组列车,总长度将超过400 m。由于高速列车外形较为复杂,考虑到计算规模,有必要对其外形进行简化。列车行驶时,气流在中间车的结构层趋于稳定,在各个中间车脉动压力情况较为一致,因此本文建立了由3节车厢组成的列车模型,包括头车、尾车和1节中间车。由于车头长度为变量,本文的列车模型长度范围为70~86 m。图2为高速列车简化模型,图3为5个长度不同的列车模型头部对比。

图2 高速列车简化模型

图3 车头长度分别为5,7,9,11,13 m时模型头部侧视图
1.3 网格划分
在列车周围2 m的空间区域采用非结构网格,流动区域的其他部分采用结构化网格。结构化网格比非结构化具有网格生成的速度快、质量好、网格数量少的特点,并且在结构化网格的生成过程中通过控制边线的节点数以及节点的分布规律,使得从高速列车由内到外网格由密变疏,以更加准确地捕捉高速列车周围的小尺度涡。因此,针对高速列车空气动力学和声场模拟过程中存在的巨大空间区域,结构化网格的应用可以极大方便地解决由非结构网格导致的数值模拟计算精度差问题。本文中不同模型的网格数量因不同车头长度的改变而不同,5 m时总网格数量约为923万个,13 m时网格数量约为1 275万个。流场域网格划分如图4所示。

图4 流场域网格划分
1.4 网格无关性验证
在简化模型2 m区域之内采用了非结构化网格,其他区域采用结构化网格。为减少由于网格带来的计算误差,保证数值模拟的精准度,取车头长度为9 m的模型,结构化网格使用4种不同数量的网格,不同网格方案的不同主要体现在非结构网格数量的差异,按照非结构网格数量从小到大分别将4种方案命名为Ⅰ,Ⅱ,Ⅲ,Ⅳ。以k-epsilon稳态流场结果下求得的阻力作为评估网格质量的指标,由表1可得。随着网格数量的增加,所得出的阻力也逐渐增大。通过相邻方案的阻力相对变化率可以看出由模型Ⅲ到模型Ⅳ,阻力变化率仅为1.0%,远小于模型Ⅱ及Ⅲ对应的5.5%和5.6%。考虑到阻力变化率和节省计算机资源,本文采用第Ⅲ种网格方案。
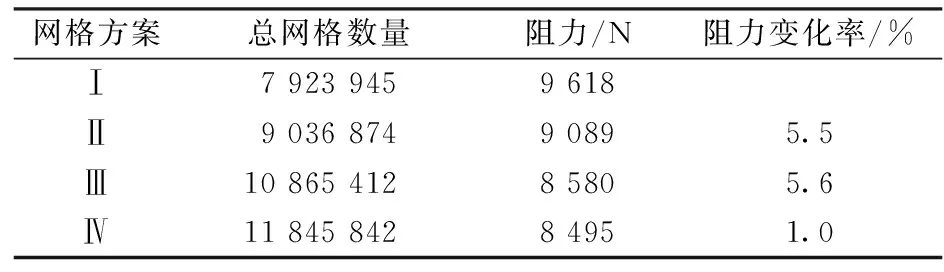
表1 不同网格方案对比
1.5 计算区域及边界条件
如图5所示,高速列车正前方来流方向截面为入口边界,设置为速度入口条件,速度为350 km·h-1。正后方截面为出口边界,设置为压力出口条件。高速列车的左侧、右侧和正上方截面设置为对称边界,列车表面设置为无滑移壁面边界。为了模拟地面效应,地面设置为滑移地面,其滑移速度为列车运行速度。列车与地面之间的距离为0.376 m。图中L,W和H分别代表高速列车简化模型的长宽高[15],整个计算域的长度为4L,宽度为24W,高为10H。
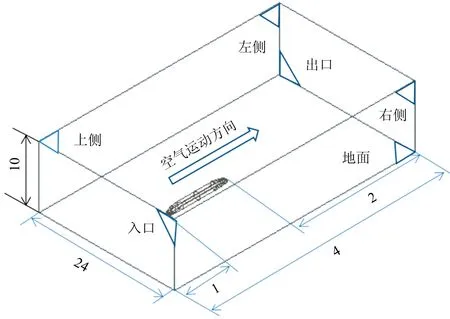
图5 计算区域尺寸(m)
2 动力特性结果
2.1 压力
由图6可知,当高速列车车头长度为5 m,速度为350 km·h-1时,车尖压力最大处达到5 665 N。随后沿车头压力逐渐降低,一直降低到负压区,在车头与车身连接处达到最小值-4 405 N,再沿车身方向压力值先小幅度上升,随后维持在1个固定值保持不变。在达到车尾与车身连接过渡区域时压力再次降低,达到与车头和车身连接过渡区域相同的负压值,并且负压区出现的区域和负压值沿车身中间面呈现对称趋势。到车尾部,压力值逐渐增大直至车尾末达到1 158 N。
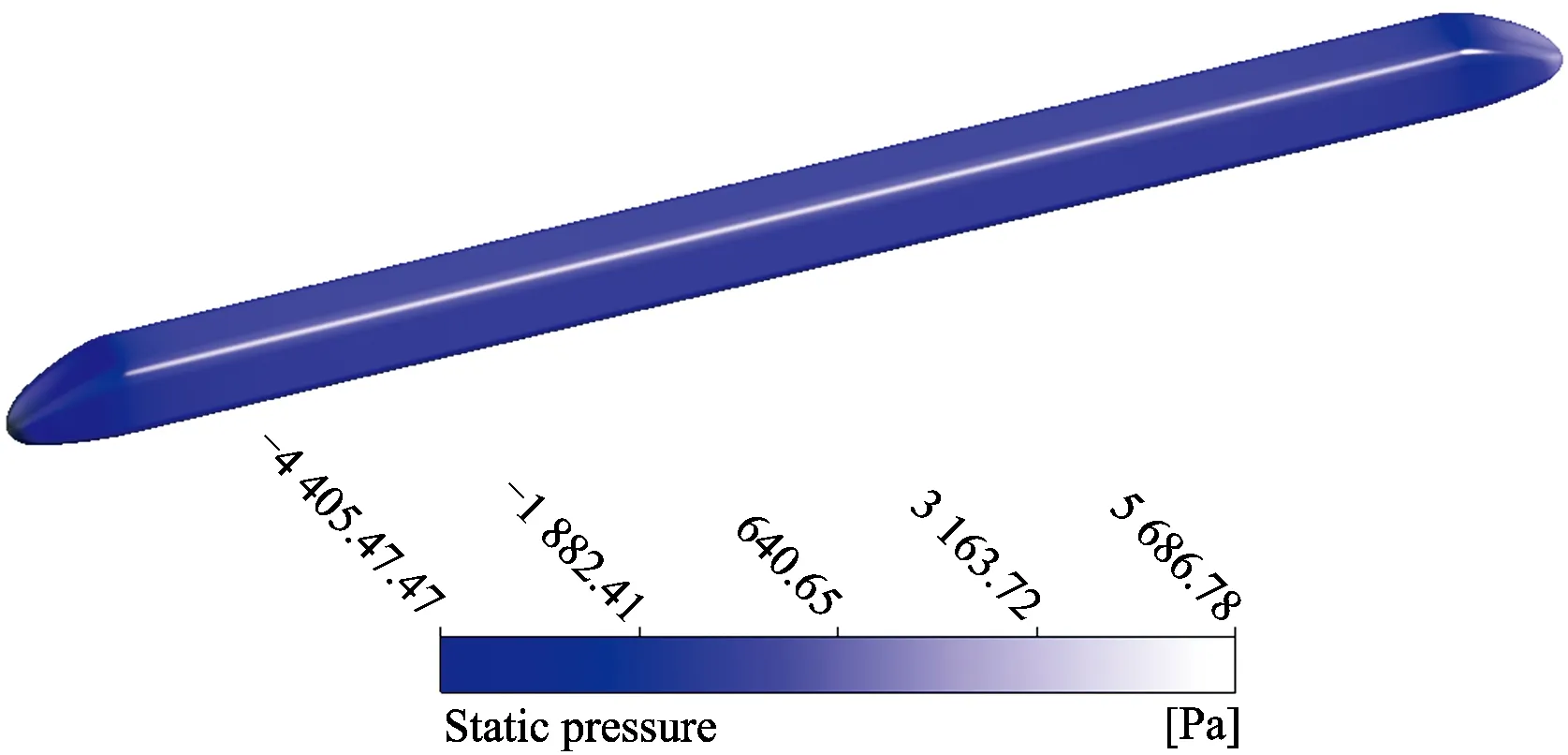
图6 车头长度为5 m时列车表面压强分布云图
对比5~13 m不同车头长度的高速列车表面压力分布均有相同的压力分布趋势,且最大压力值保持在5 560~5 750 N之间(因计算误差有小幅度波动),但最小压力值呈现逐渐增大的趋势。若曲线拟合方程为Y=-9 702.571 43+1 337.428 57x-52.857 14x2,则R2=0.988 6。拟合曲线如图7所示。
2.2 阻力和升力
由图8可知随着车头长度的增加,气流的分离减弱,压差阻力呈现减小趋势,变化趋势趋向平缓,由5 m时的2 649.37 N减小至13 m时的500.46 N。摩擦阻力呈线性上升趋势,由5 m时的6 457.21 N增长到13 m时7 327.75 N。在压差阻力和黏性阻力的综合作用下总阻力呈现出先减小后增大的趋势。由此可得,通过增加车头长度来减少阻力会有1个极限值,过大的车头长度反而会使得阻力增加。
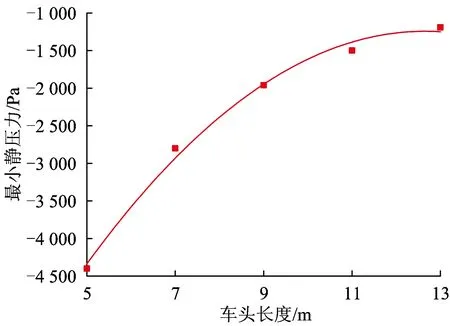
图7 最小静压力随车头长度的变化
气动阻力拟合曲线方程:
Y=6 424.59-963.64x+39.36x2,
R2=0.979
摩擦阻力曲线拟合方程:
Y=5 923.95+107.79x,R2=0.998
总阻力曲线拟合方程:
Y=15 462-2 037.88x+179.02x2-5.19x3,R2=0.988
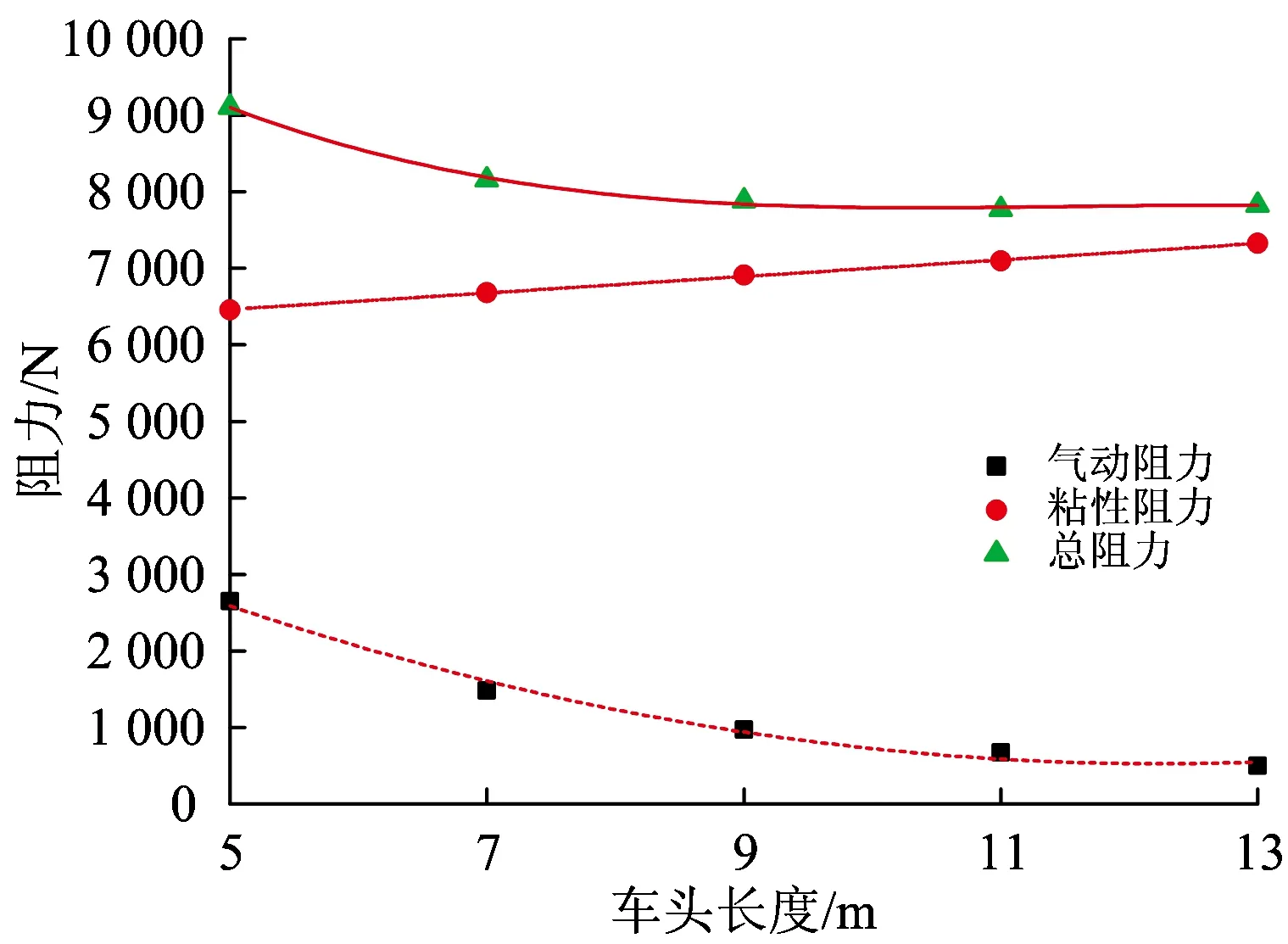
图8 阻力随车头长度变化曲线
由图9可知高速列车车头长度为5 m,是升力的绝对值,最大为598.34 N。将车头长度为7~15m的列车模型升力值取绝对值之后,均小于200 N,并无明显差异。这表明车头长度过小将导致升力的绝对值过大,车头长度大于等于7 m之后升力的绝对值趋于稳定。负的升力值让列车在轮轨上平稳行驶,但如果负升力值过大,将产生过大的摩擦阻力,为克服摩擦阻力将消耗过多的电力资源。
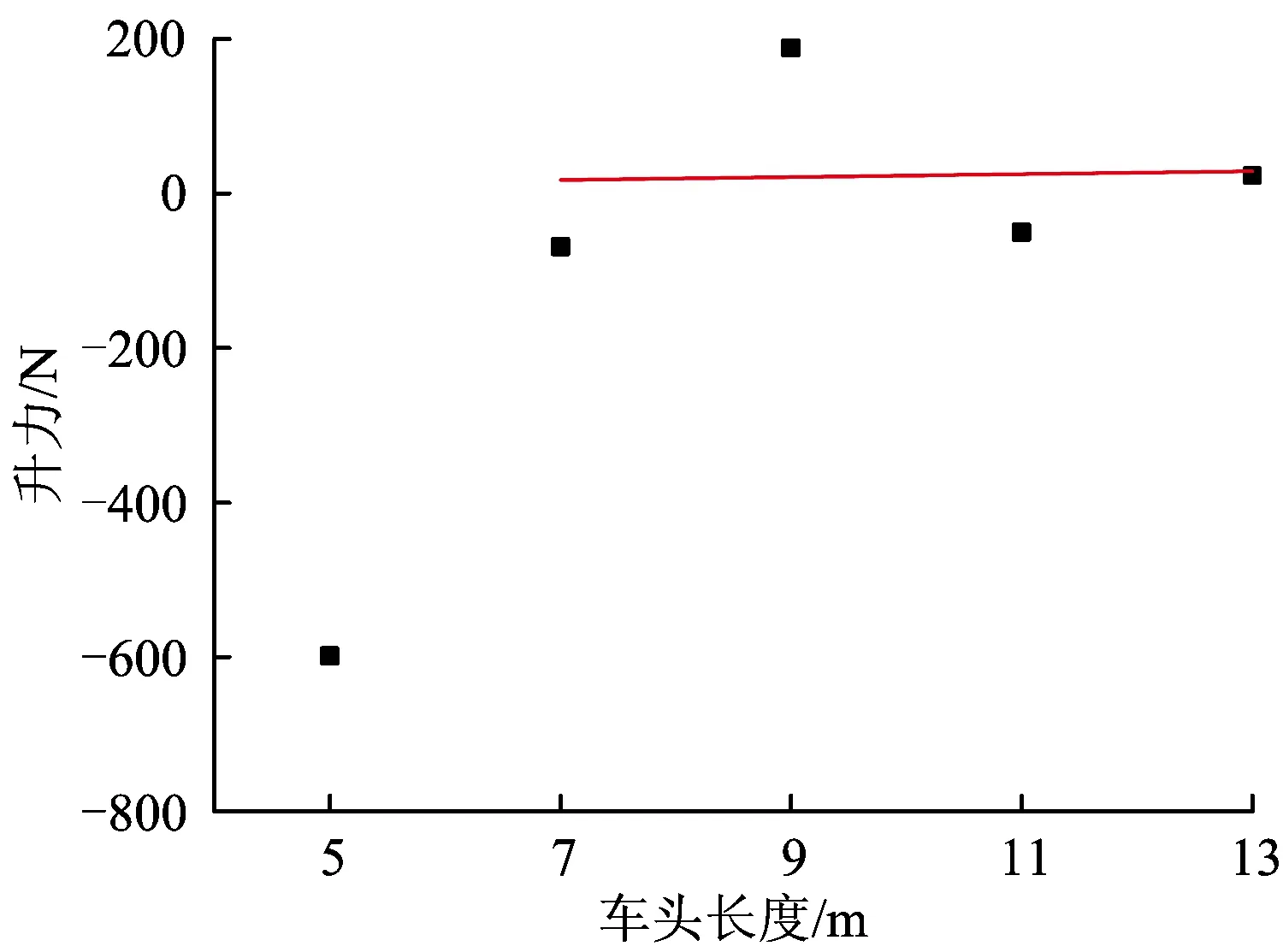
图9 升力随车头长度变化趋势
3 气动噪声
3.1 声功率级分布特性
对比5~13 m不同长度的高速列车简化模型表面偶极子声功率级分布云图可知,列车表面的最大声功率级出现在车头部位,车身部位的声功率级比车头部位进一步减小,并且保持一定,不随车身变化。车身与车尾连接处声功率级较大,直至车尾尽头声功率级处于比较低的水平。随着车头长度的增加,车头部位最大声功率级呈现出减小趋势,两者的关系接近线性,如图11所示。若拟合函数定义为y=-0.955x+106.33,则R2=0.97。而车身部分并无差别,车身与车尾连接处声功率级呈现出减小趋势,尾车的声功率级分布更加均匀。
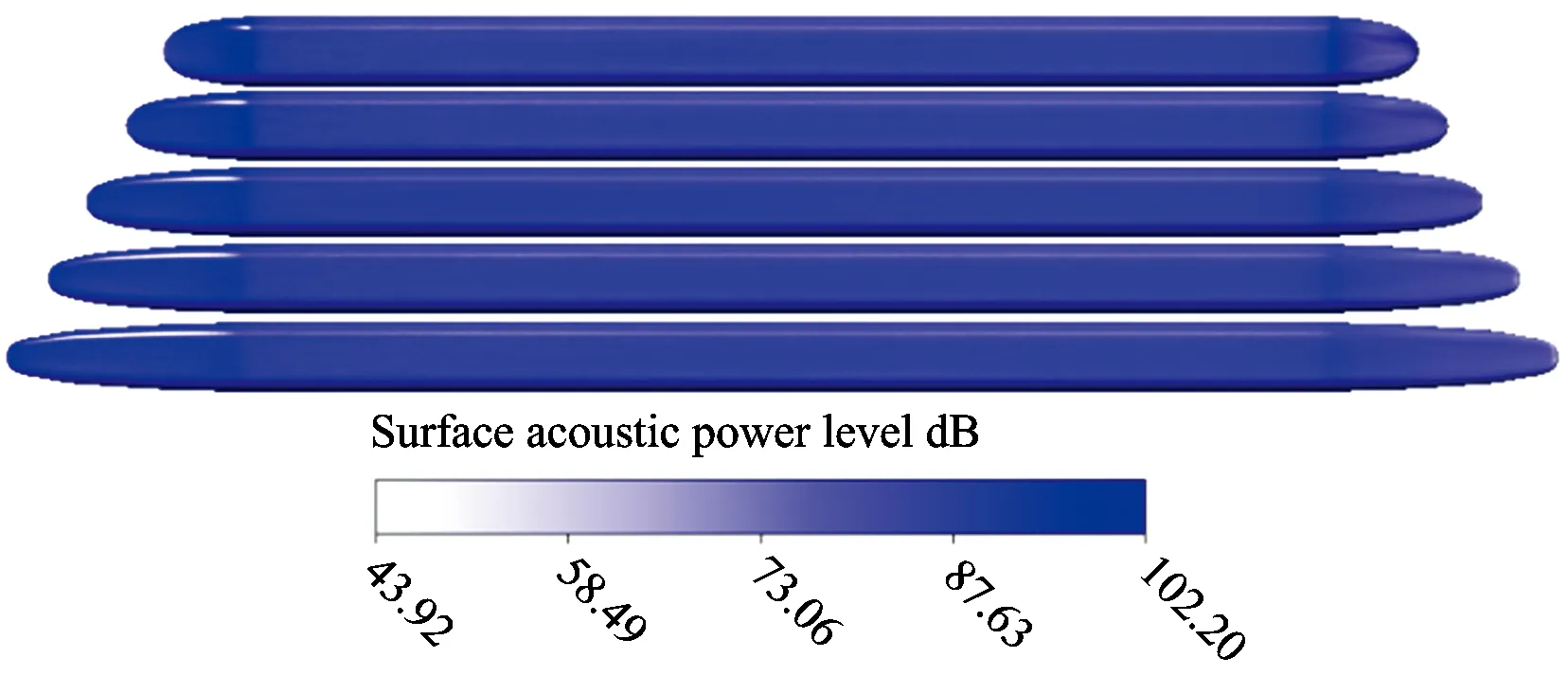
图10 5~13 m长度车头的列车表面声功率级分布对比云图
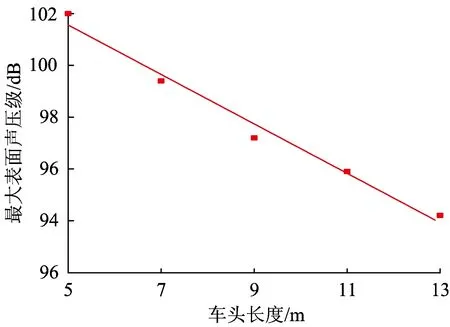
图11 最大声功率级随车头长度变化趋势
3.2 远场气动特性
根据数值模拟所得到的声场结果,在距轨道25 m远、距地面高3.5 m的区域,布置11个监测点,列车行驶方向依次为1~11监测点,如图12所示。监测点3和9分别对应车身段的起点和终点,监测点2和点10分别对应列车的起点和终点,相邻监测点之间的距离为10 m。
图12 远场气动噪声数值仿真监测点分布示意图
从图13可以看出,随着车头长度的增加,点1和点11的声压级呈现出减少趋势。点1声压级减少趋势较为缓和,总共下降3.67 dB,而车头长度从5 m到7 m点11声压级下降较大,达到7.06 dB,随后大致保持不变;点2和点10声压级并无明显变化,和车身部位相对应的监测点总体上呈现出增大趋势,由9 m至11 m声压级增大幅度最大。由于高速列车模型为简化模型,并没有包括轮毂、转向架和受电弓等复杂的结构,因此仿真得到的声压级较小。
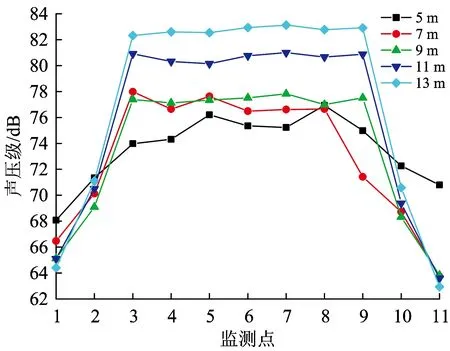
图13 各个数值仿真监测点声压级随车头变化情况
针对和车身部位相对应的监测点3—9呈现出的增大趋势,为更好地对比其差别,将车头长度一定时的这7个监测点求和之后取平均值,如图14所示。由图可见,随着车头长度的增加,车身部位所对应监测的平均声压级呈现出非线性的增加趋势,车头长度在5~13 m范围内,声压级增长幅度呈增大趋势,若拟合方程为Y=75.94-0.95x+0.087x2,则R2=0.953 5。
由7个声压级监测点可以看出高速列车远场声压级的大致规律,车身对应的监测点声压级大致相等,沿两端方向声压级开始逐渐降低,沿头车方向比沿尾车方向声压级降低缓慢。一般认为,高速列车气动噪声的生成和其表面的脉动压力有关,现对其进行分析。
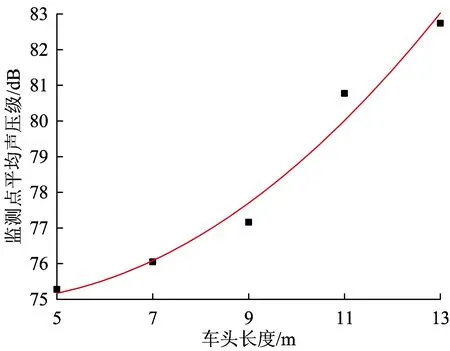
图14 车身部位所对应数值仿真监测点的平均声压级
图15中(a)—(e)分别列出了5~13 m高速列车中轴线的纵向和水平横截面动压力云图。由图可知,车体附近的脉动压力值较大,且沿着中轴线成对称分布,脉动压力的最大值出现在车身与车头、车尾的连接处,此处曲面的曲率变化大,旋涡脱落较大,气流扰动较为剧烈。随着车头长度的增加,连接处的曲面曲率值减小,最大脉动压力值呈现出减小趋势。脉动压力影响的范围也出现了变化,沿横向的影响范围减少,但随着车头长度的增加,较大动压在纵向的影响区域变大。由此可知,高速列车附近的脉动压力值的大小和分布状况决定了监测点的声压级,脉动压力在纵向上的增加会使得车身所对应的监测点声压级迅速上升,可知通过控制高速列车车头的长度,不仅可影响气动噪声的影响范围,还可减少远场监测点的声压级。
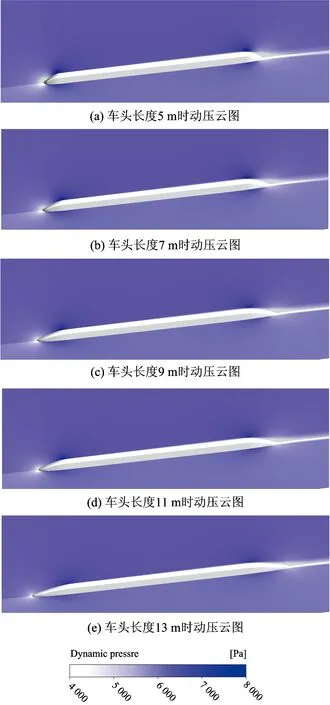
图15 高速列车周边脉动压力随车头长度变化对比云图
车头长度为9 m,速度为350 km·h-1时数值仿真监测点6的频谱图如图16所示。由(a)可知远场监测点的声压级在很宽的频率内存在,低于400 Hz时声压级逐步增大,400~1 600 Hz时声压级呈现出由大变小的趋势,1 600~5 000 Hz范围内声压级值较为稳定。为了使声音的客观物理量和人耳听觉感受近似取得一致,人们一般对测量得到的声音进行A计权处理,将其进行A计权之后噪声低频成分进行衰减,所得结果如图(b)所示。低频所占的比重降低,从低频到高频声压级逐渐升高,当频率到达1 000 Hz时所对应的声压级最大为65.5 dB,1 000~5 000 Hz时A计权声压级缓慢减小。
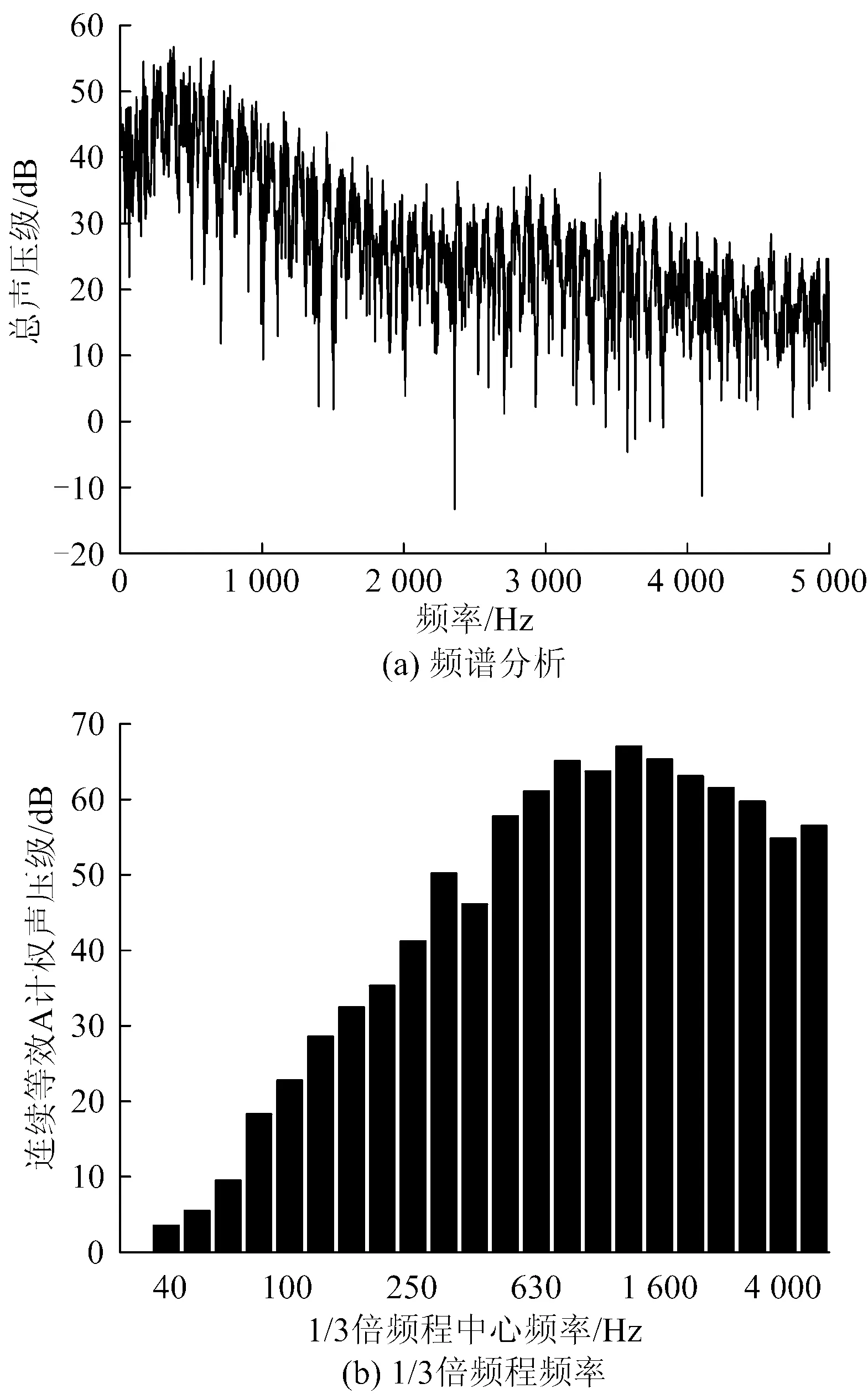
图16 车头长度为9 m时数值仿真监测点6的频谱图
将车头长度分别为5和13 m时远场监测点6的频谱图相对比可得声压级的增大在一个很宽的频率范围内存在,如图17所示。在低于300 Hz时13 m所对应的声压级有所降低,在300~700 Hz范围内两者基本持平,在700~5 000 Hz范围内13 m所对应的声压级大于5 m时,在1 400~2 250 Hz范围内13 m所对应的声压级超出5 m的较多。
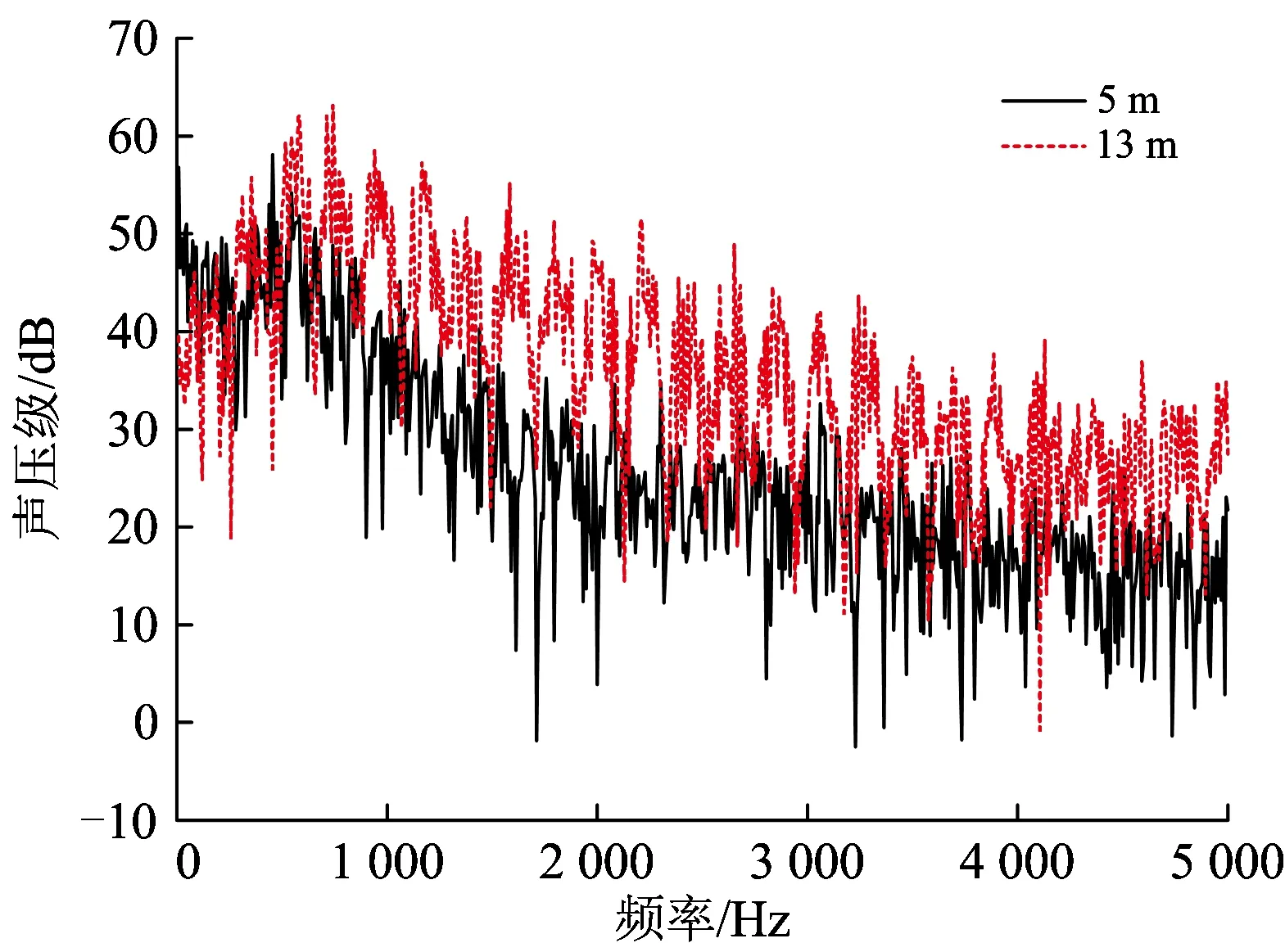
图17 车头长度分别为5和13 m时监测点6的频谱对比
在车头长度为9 m,速度为350 km·h-1时模型车头鼻尖处设置脉动压力监测点,在得到充分震荡的脉动压力时程曲线以后,进行傅里叶变换得到监测点的声压频谱图,脉动压力时程曲线图均呈现出类似图18所示的波动,脉动压力的峰值有所差异,所得结果和图15中相同。频谱图均呈现出图19的趋势,各点的气动噪声在很宽的频谱内存在,无明显主频率,随着频率的增大,幅值逐渐减小。
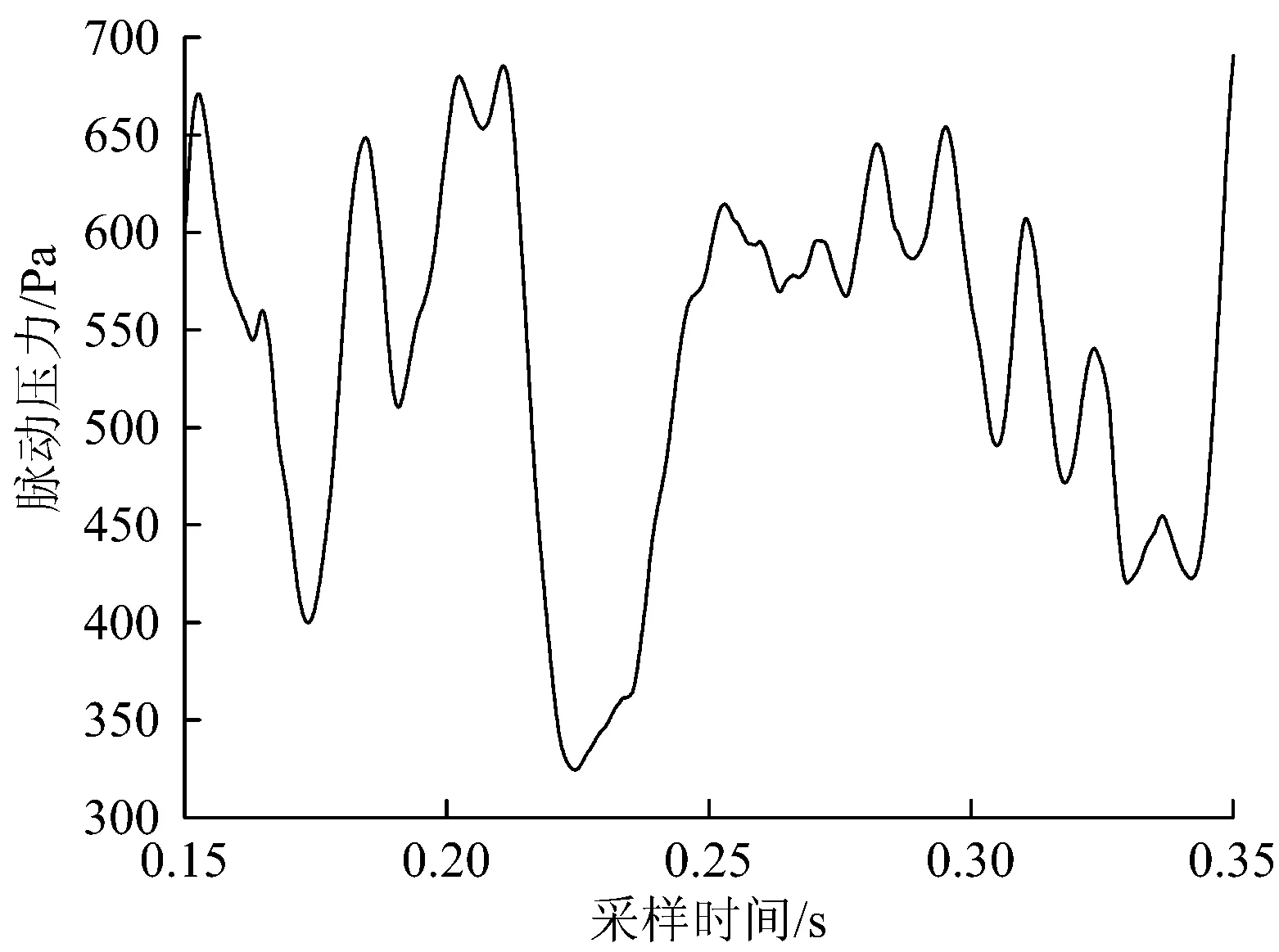
图18 车头长度为5 m时数值仿真监测点1的脉动压力时程曲线
为得到本模型下最佳的车头长度,根据数值模拟计算得到的阻力变化规律(图8)和远场噪声监测点的平均声压级(图14),表2列出了随着车头长度的变化阻力相对降低率和声压级的相对增长率。从表2中可以看出,车头长度由9 m到11 m阻力相对降低率为最低1.4%,而声压级的增长率达到最大为4.7%,由此可得在此模型下最佳的车头长度为9 m。
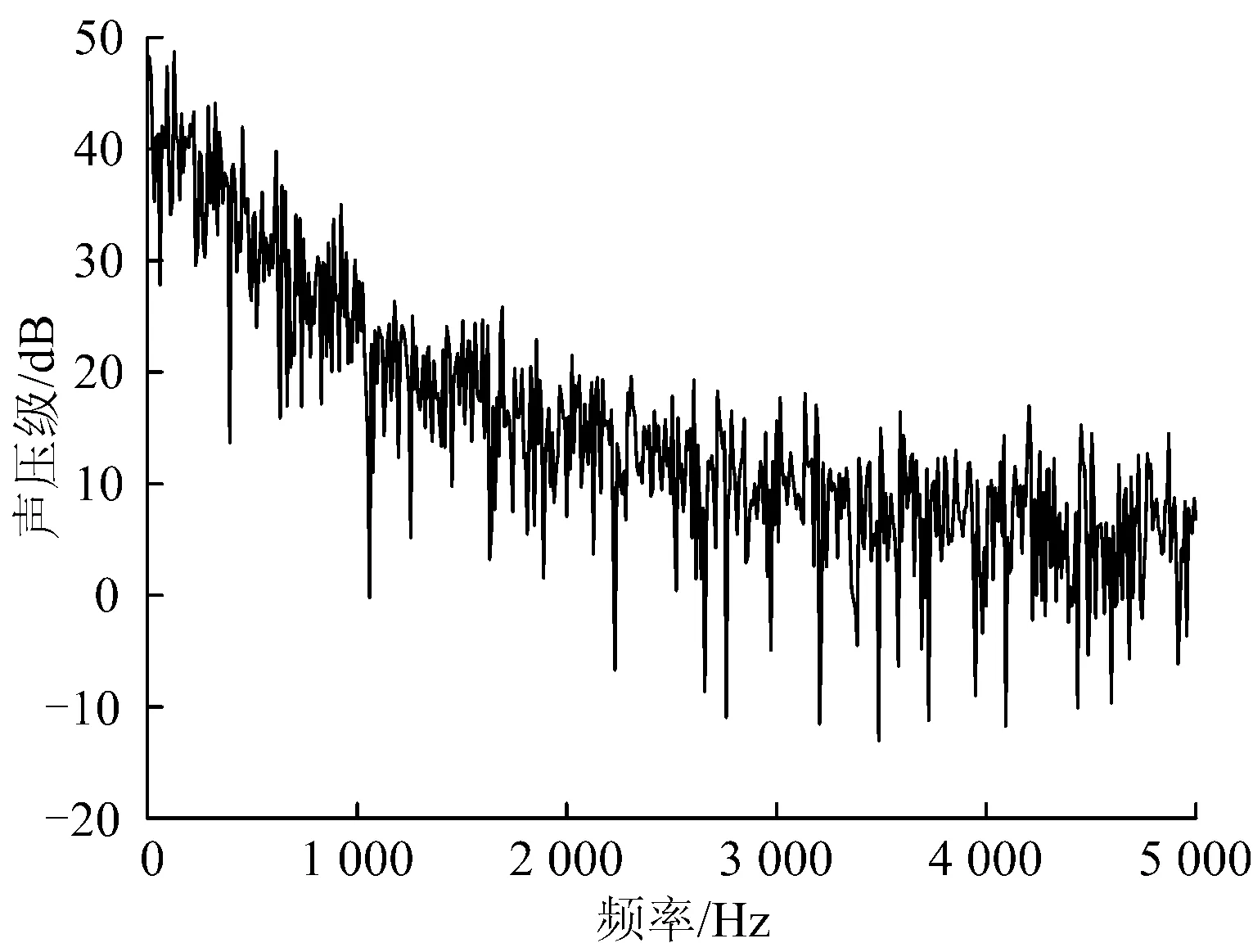
图19 车头长度为5 m时数值仿真监测点1声压级频谱
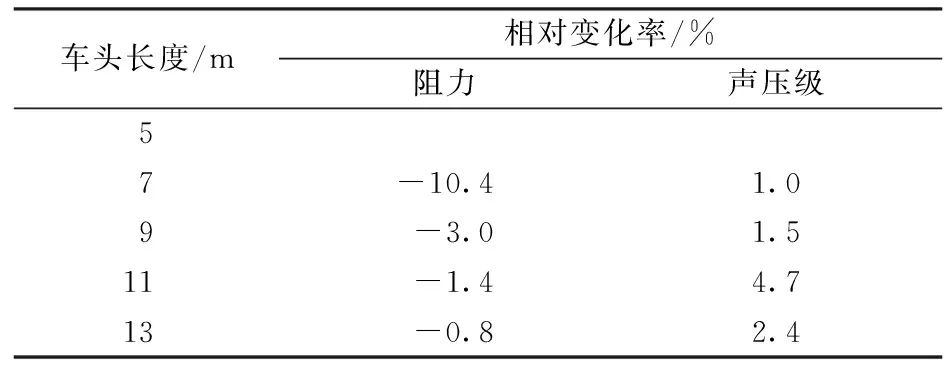
表2 阻力和声压级随车头长度变化规律对比
4 结 论
(1)高速列车的阻力随着车头长度的增加呈现出先减小后增大的趋势,因为压差阻力随着车头长度的减少是有限的,而黏性阻力与车头长度成线性关系。高速列车的升力随着车头长度的增加亦呈现出先减小后增大的趋势。
(2)随着车头长度的增加,车头部位最大声功率级呈现出减小趋势,关系接近线性,而车身部分并无差别,车身与车尾连接处声功率级呈现出减小趋势,尾车的声功率级分布更加均匀。
(3)数值模拟监测点的平均声压级呈现出非线性的增加趋势,结合阻力的变化趋势,可得最佳的车头长度为9 m,在此车头长度下阻力尚未开始增长,远场数值模拟监测点的平均声压级的增加幅度并不大,即可减小行车阻力同时控制噪声对环境的污染。
(4)随着车头长度的增加,高速列车附近的最大动压值逐渐减小,在模型表面设置的数值模拟监测点呈现出随机震荡,进行傅里叶变换之后,随着频率的增大,声压级幅值逐渐减小;远场数值模拟监测点声压级的增大,是由于在700~5 000 Hz范围内声压级的增大导致。
