基于ALE方法的高速轮轨黏着特性仿真及试验验证
2018-10-13蔡园武常崇义
蔡园武,常崇义,陈 波,李 兰
(1.中国铁道科学研究院 铁道科学技术研究发展中心,北京 100081;2.中国铁道科学研究院 高速轮轨关系试验室,北京 100081)
轮轨黏着是铁道车辆运行的基础。车辆的运行性能,包括起动、加速、减速和停车都是由轮轨黏着特性决定的。随着列车速度的不断提高,对轮轨黏着特性的要求也随之提高,对高速轮轨黏着的深入研究也更加迫切。
目前常用的轮轨蠕滑率/力理论是Kalker的线性蠕滑率/力模型[1]及其简化理论[2]和CONTACT程序[3]。Kalker理论采取了一些假设,如弹性半空间假设、同一性假设、惯性力假设、摩擦系数假设等。但是,根据后来的理论和试验研究结果[4-9],微滑区的结果和Kalker理论较为一致,而滑动区的结果则差别较大。有限元方法可以考虑轮轨真实几何、材料、接触非线性等,不受半空间假设的限制。但是,传统的基于拉格朗日(Lagrange)网格的有限元方法需要在所有可能的接触区划分非常细的网格。如果想要获得轮轨滚动接触的稳态解,需要沿车轮周向和很长一段钢轨的接触表面都划分细网格,造成模型的规模非常庞大。为了解决这一困难,文献[10—12]采用任意的拉格朗日-欧拉方法(ALE方法)求解轮轨滚动接触问题。这种方法相比传统有限元方法,不需要在车轮周向和钢轨的接触面上划分非常细致的网格,能够大大减小模型规模,提高计算效率。文献[13]采用ALE方法建立了轮轨滚动接触模型,分析了稳态时轮轨接触斑状态,但是仅考虑了车轮自然滚动时的情况,并没有对高速轮轨牵引、制动过程中的黏着特性进行分析。
本文根据全尺寸高速轮轨关系试验台中黏着轮(模拟车轮)与轨道轮(模拟钢轨)的滚动接触,建立了基于ALE方法的轮轨滚动接触三维有限元模型,利用该模型仿真分析了干燥条件下的高速轮轨黏着特性曲线,并利用高速轮轨关系试验台的高速黏着试验结果对其进行了验证。利用验证后的模型分析了轮轨接触状态随纵向蠕滑率的变化规律,探讨了轮轨摩擦系数与黏着特性曲线的关系。
1 基于高速轮轨关系试验台的轮轨黏着试验
利用中国铁道科学研究院全尺寸高速轮轨关系试验台完成高速轮轨黏着试验,试验台黏着试验的装配如图1所示。在黏着试验中,首先施加垂向载荷,由轨道轮电机驱动轨道轮,轨道轮通过与黏着轮接触,逐渐地使轨道轮和黏着轮接触点处的速度达到指定的试验速度。然后黏着轮电机以一定速率增加扭矩,同时轨道轮电机处于恒速状态,连续测量轮轨纵向蠕滑率和纵向蠕滑力。逐渐增加黏着轮电机扭矩,直到纵向蠕滑率增加而纵向蠕滑力不再增加反而减小时,表明纵向蠕滑力已达到饱和状态,此时停止试验。

图1 试验台黏着试验装配图
在试验中,纵向蠕滑力系数μ可由下式计算得到。
(1)
式中:F为轮轨接触点纵向蠕滑力;FN为轮轨接触点正压力;Mw为黏着轮扭矩;Rw为黏着轮滚动圆半径;αw为黏着轮角加速度;Iw为黏着轮的转动惯量。
纵向蠕滑率ξ1为
(2)
式中:vw和vr分别为黏着轮和轨道轮在接触点处的线速度;ωw和ωr分别为黏着轮和轨道轮的滚动角速度;rw和rr分别为黏着轮和轨道轮的瞬时滚动圆半径。
2 基于ALE方法的轮轨滚动接触三维有限元模型
根据图1所示全尺寸高速轮轨关系试验台的黏着试验装配情况,建立基于ALE方法的轮轨滚动接触三维有限元模型如图2所示。该模型与文献[13]的类似,不同之处是本文模型是根据全尺寸高速轮轨关系试验台黏着轮和轨道轮实物建立,黏着轮模型采用S1002CN型踏面,直径为920 mm;轨道轮模型采用60廓形,直径为3 000 mm,轨底坡为1/40;黏着轮和轨道轮的弹性模量为210 GPa,泊松比为0.28,密度为7 800 kg·m-3;轮轨间静摩擦系数为0.486;黏着轮横移量为0 mm,冲角为0 mrad,轴重为10 t。由于远离轮轨接触点部位对轮轨接触的影响很小,模型中轨道轮只考虑接触点附近的一部分。

图2 基于ALE方法的轮轨滚动接触三维有限元模型
轮轨间摩擦系数采用Bochet[14]根据Poiree在里昂铁路上车辆沿钢轨滑动的制动试验数据(试验速度高达22.0 m·s-1)得出的轮轨动摩擦系数与相对滑动速度的经验公式,为
(3)
式中:μs为静摩擦系数;μk为动摩擦系数;Δv为相对滑动速度。
3 轮轨黏着仿真分析与模型验证
3.1 仿真黏着特性曲线与试验结果对比
利用全尺寸高速轮轨关系试验台开展了轮轨干燥状态、速度为380 km·h-1和轴重为10 t时的牵引、制动工况下的轮轨黏着蠕滑过程,结果如图3所示。图中:纵向蠕滑率为正表示牵引工况,为负表示制动工况。从图3的试验结果看出:在牵引状态下,当纵向蠕滑率小于3‰时,纵向蠕滑力近似线性增长;当纵向蠕滑率大于3‰后,纵向蠕滑力随纵向蠕滑率呈非线性增长,在纵向蠕滑率约为6‰时达到最大值,然后纵向蠕滑力随纵向蠕滑率的增加而减小;制动过程的黏着特性曲线与牵引过程的黏着特性曲线规律是相似的。
从图3中仿真与试验结果的对比看出:在小蠕滑范围里,纵向蠕滑力随纵向蠕滑率的线性变化关系及其变化斜率的仿真与试验结果基本一致;纵向蠕滑力出现最大值及其饱和点时的纵向蠕滑率仿真与试验结果基本吻合;仿真与试验结果都显示纵向蠕滑力达到最大值以后,其随纵向蠕滑率的增加而减小。但是,当纵向蠕滑率从3‰到6‰(饱和点)的变化过程中,试验结果中纵向蠕滑力随纵向蠕滑率呈非线性增长,而仿真结果却呈线性增长。差异产生的主要原因是:基于ALE方法的仿真模型是稳态假设的,该模型无法考虑由于轮轨间摩擦或相互作用产生的振动,及其对轮轨黏着的影响。

图3 牵引制动黏着特性曲线
通过速度为380 km·h-1时轮轨黏着仿真与试验结果的比对分析,说明基于ALE方法的高速轮轨滚动接触三维有限元模型可以用于分析干燥轮轨接触表面条件下轮轨黏着特性曲线的基本特征,更重要的是利用验证后的模型可以进一步分析轮轨牵引制动过程中的轮轨接触应力、摩擦力分布,以及用于轮轨黏着机理方面的分析。
3.2 轮轨黏着过程中的接触状态
利用基于ALE方法的高速轮轨滚动接触三维有限元模型获得轮轨接触斑内各点接触状态随纵向蠕滑率的变化规律如图4所示。

·—黏着;+—滑动;∘—未接触
从图4看出:接触斑是1个近似的三角形,而不是标准椭圆形,这与黏着轮和轨道轮的实际非线性几何形状有关;当纵向蠕滑率很小时,轮轨接触斑内所有点都属于黏着区;随着纵向蠕滑率增大(牵引工况)或减小(制动工况),接触斑内出现黏着区和滑动区共存的现象,当纵向蠕滑率为-0.4%(制动工况)时接触斑靠近轮缘的一侧为黏着区、远离轮缘的一侧为滑动区,当纵向蠕滑率为0.4%(牵引工况)时接触斑靠近轮缘的一侧为滑动区、远离轮缘的一侧为黏着区;当纵向蠕滑率增大或减小到超过饱和点(0.6%)后,黏着区就会消失,接触斑内全部变成滑动区。值得注意的是,当黏着区和滑动区共存时,计算得到在牵引和制动工况下的黏着区正好相反地位于接触斑横向的一侧,这是由于实际黏着轮踏面曲率不同以及滚动圆半径差造成的。
接触斑内摩擦应力随纵向蠕滑率的变化如图5—图8所示。从图5(c)和图6(c)看出:纵向蠕滑率为0%时(黏着轮自由滚动时),接触班内的纵向摩擦应力和横向摩擦应力有正有负,数值较小。从图5看出:随着纵向蠕滑率的增加(牵引时)或减小(制动时),纵向摩擦应力方向趋于一致的向前(牵引时)或向后(制动时),其数值逐渐增大到最大值。从图6看出:横向摩擦应力随着纵向蠕滑率变化不大,且数值较小。从图7看出:随着纵向蠕滑率增加或减小,总摩擦应力数值主要取决于纵向摩擦应力,逐渐增大到最大值。从图8看出:摩擦力方向逐渐趋于一致的前进(牵引时)或后退(制动时)方向,自旋现象逐渐消失;合成的总摩擦力矢量方向表现为绕接触斑内某一点自旋,旋转中心点处摩擦力小,靠近轮缘侧摩擦力大。

图5 纵向摩擦应力随纵向蠕滑率的变化过程

图6 横向摩擦应力随纵向蠕滑率的变化过程
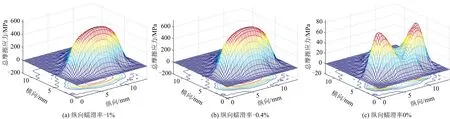

图7 总摩擦应力随纵向蠕滑率的变化过程

图8 总摩擦应力矢量随纵向蠕滑率的变化过程
轮轨牵引制动过程中接触点中心点处纵切面上的工程应力(Mises应力)云图如图9所示。从图9看出:Mises应力随纵向蠕滑率增加而增大,最大应力点由轮对自由滚动时(蠕滑率为0%)的接触表面以下2mm处转移到接触表面,最大Mises应力从自由滚动时的920 MPa变化到纵向蠕滑率1%时的1 208 MPa,应力更加集中。Mises应力分布变化的原因是:自由滚动时,摩擦力很小,Mises应力主要由法向接触压力产生,这与静止状态时的轮轨接触现象基本一致;纵向蠕滑率逐渐增大后,摩擦力也在逐渐增大,其与法向接触压力共同作用产生的Mises应力也逐渐增大,且Mises应力最大值位置向摩擦力最大位置靠近。

图9 Mises应力随纵向蠕滑率的变化过程
3.3 轮轨摩擦系数与黏着特性曲线之间的关系
本文采用的摩擦系数是轮轨相对滑动速度的函数,见式(3),随着轮轨相对滑动速度的增加,摩擦系数逐渐减小。黏着特性曲线是纵向蠕滑力系数关于纵向蠕滑率的曲线,而纵向蠕滑率也是相对滑动速度的函数,见式(2)。如果想对摩擦系数与黏着特性曲线进行比较,那么需要对其公式进行一定的变换。
轮轨相对滑动速度为
Δv=vw-vr
(4)
则式(2)可转换为
(5)
或
(6)
代入式(3),得到动摩擦系数关于纵向蠕滑率的函数即动摩擦系数曲线为
(7)
通过以上推导,可以把动摩擦系数曲线与仿真得到的黏着特性曲线进行对比分析,结果如图10所示。从图10看出:小蠕滑时纵向蠕滑力系数随纵向蠕滑率的增加近似呈线性增长,达到饱和点后,在轮轨相对滑动速度相同时纵向蠕滑力系数大于动摩擦系数,该差别随着纵向蠕滑率的增加而逐渐减小。

图10 黏着特性曲线与动摩擦系数曲线对比
纵向蠕滑力系数随纵向蠕滑率增加逐渐逼近动摩擦系数的原因如下。接触斑内黏着区和滑动区共存,纵向蠕滑力由2个区域产生的摩擦力共同贡献,如式(8)所示。
(8)
式中:ΩA为黏着区;ΩS为滑动区;Fi为黏着区内i点的纵向摩擦力;μi为滑动区内i点的动摩擦系数;FNi为滑动区内i点的正压力;θ为总摩擦力方向与纵向的夹角。
滑动区的摩擦力由给定的动摩擦系数公式计算得到,而黏着区的摩擦力则与接触面的变形有关。小蠕滑时,滑动区较小,因此纵向蠕滑力系数和动摩擦系数公式差别较大。随着纵向蠕滑率的增加,滑动区逐渐增大,纵向蠕滑力系数越来越逼近动摩擦系数。
另一方面,从总摩擦力的方向来看(如图8所示),小蠕滑时,总摩擦力矢量方向表现为绕接触斑内某一点自旋,随着纵向蠕滑率增加,总摩擦力方向逐渐趋于一致,自旋现象逐渐消失。因为纵向摩擦力是总摩擦力沿纵向的分量,随着纵向蠕滑率的增加,其数值逐渐接近总摩擦力,因此由纵向摩擦力计算出的纵向蠕滑力系数也逐渐趋近于动摩擦系数。
不同纵向蠕滑率时接触斑内的相对滑动速度如图11所示。由图11看出:随着纵向蠕滑率增加,相对滑动速度逐渐增大,且滑动区内各点的相对滑动速度趋于一致,因此这些点的动摩擦系数趋于相等,这也导致纵向蠕滑力系数趋于动摩擦系数。

图11 纵向相对滑动速度随纵向蠕滑率的变化过程
这一结果为预测大蠕滑率时的纵向蠕滑力系数提供了参考。小蠕滑率的黏着特性曲线可以由试验室试验得到,但是试验室进行的黏着试验一般在蠕滑率1%以内,较少进行大蠕滑率试验(大蠕滑率试验容易造成黏着轮和轨道轮的擦伤)。如果通过试验获得了滑动摩擦系数的变化规律,就可以代替大蠕滑率时的黏着试验。
4 结 论
(1)基于全尺寸高速轮轨关系试验台中黏着轮与轨道轮的滚动接触,建立了基于ALE方法的轮轨滚动接触三维有限元模型,利用该模型仿真分析了干燥条件下的高速轮轨黏着特性曲线,仿真结果与试验结果基本吻合,表明该模型可用于干燥条件下轮轨黏着特性仿真分析。
(2)从黏着轮自由滚动的全黏状态进入牵引或制动全滑动状态时,在牵引工况时接触斑靠近轮缘的一侧先进入滑动状态,而制动工况时则远离轮缘的一侧先进入滑动状态。
(3)黏着轮自由滚动时,摩擦力方向表现为绕接触斑内某一点自旋,摩擦力数值相对较小;随着纵向蠕滑率增加或减小,摩擦力方向逐渐趋于一致的前进(牵引时)或后退(制动时)方向,自旋现象逐渐消失,摩擦力数值逐渐增大到最大值。
(4)Mises最大应力点由轮对自由滚动时的接触表面以下2 mm处转移到接触表面,应力更加集中。
(5)通过动摩擦系数和黏着特性曲线的比较分析,发现纵向蠕滑力系数达到饱和点之后,在轮轨相对滑动速度相同时纵向蠕滑力系数大于动摩擦系数,该差别随着纵向蠕滑率的增加而逐渐减小。
