一种可移动检测机器人站位规划策略

林晓青,杨继之,乐 毅,张 斌

(北京卫星制造厂有限公司，北京 100094)

0 引 言

在航空航天、船舶、能源等重大工程领域的核心装备制造过程中，普遍存在一类空间尺寸大、精度指标要求高、加工难度大的大型构件。传统的基于大型龙门式加工中心的制造模式已无法满足这类产品的制造需求。可移动机器人的解决方案能够在满足制造要求的条件下大大提高生产效率、降低成本[1-2]。目前，可移动机器人的研究领域主要集中在钻孔和紧固[3-4]、装配[5]、铣削[6]。对于这些非结构化的制造模式，如何确定可移动机器人的工作站位并能满足制造过程中效率、安全性、精度等一系列约束条件，是这种柔性制造系统在应用过程中亟需解决的问题。

针对机器人站位规划问题，国内外学者已开展了相关的研究工作。Mitsi等[7]以工作空间与关节转角限位为约束条件，基于改进遗传算法和拟牛顿算法对机器人站位和关节转角进行优化。Huang等[8]将机器人选型和机器人站位同时作为多机器人系统集成设计指标，利用多目标粒子群优化算法进行参数优化，基于M/M/1排队模型进行优化结果评估，规划效率相较于传统的人工经验提高了20倍。Tao等[9]针对某型号飞机壁板装配过程多机器人单元，将机器人工作空间定义为扇形区域，以最大化两机器人无碰撞重叠区域为目标对机器人工作单元布局问题进行非线性规划。王军等[10]在上述方法的基础上引入了遗传算法，克服了求解优化布局时传统非线性规划算法的缺陷，提高了优化质量。田威等[11]针对附加外部轴的工业机器人自动钻铆系统提出了一种分站式规划策略，并结合待加工点的位姿信息和加工工艺要求，对机器人的转站机制进行建模和优化。文献[12-14]针对喷涂机器人站位规划问题，以腕心为假想基座建立机器人反向运动链，通过求解各个目标点的空间交集得到站位可行区域，并基于可操作度和平稳性指标优化站位。

然而，上述方法仅仅针对作者搭建的系统或是满足特定的任务需求，对于面向航天器大型舱体舱外支架三维检测的可移动检测机器人而言，无论是检测对象的复杂性，还是机器人应用过程中对效率、安全性、精度的要求，都对站位规划策略都提出了新的要求。目前在航空航天等重大工程领域，尚无面向可移动检测机器人的站位规划策略，这在一定程度上限制了可移动检测机器人系统的实际应用。

因此，在以上文献的研究基础之上，本文聚焦于航天器大型舱体舱外支架三维检测任务，以检测视点的空间范围和可移动检测机器人工作空间为约束，分别基于舱体轴向和径向建立机器人工作区域划分数学模型。在此基础上，将工作区域栅格化处理并结合机器人逆运动学，以逆运动学有解且满足轴限位为约束，得到可行解。针对多组可行解提出基于机器人关节加权方差的算法进一步优化站位。

1 问题描述

载人航天器大型密封舱体均为焊接结构，舱体焊后变形难以避免。为了满足舱外设备的安装精度要求，采用基于可移动机器人的柔性制造系统对预留一定余量的支架进行原位加工。因此，需要确定待加工面相对于舱体基坐标系的位姿关系以及设备安装面上螺纹孔位等特征的相互位置关系。

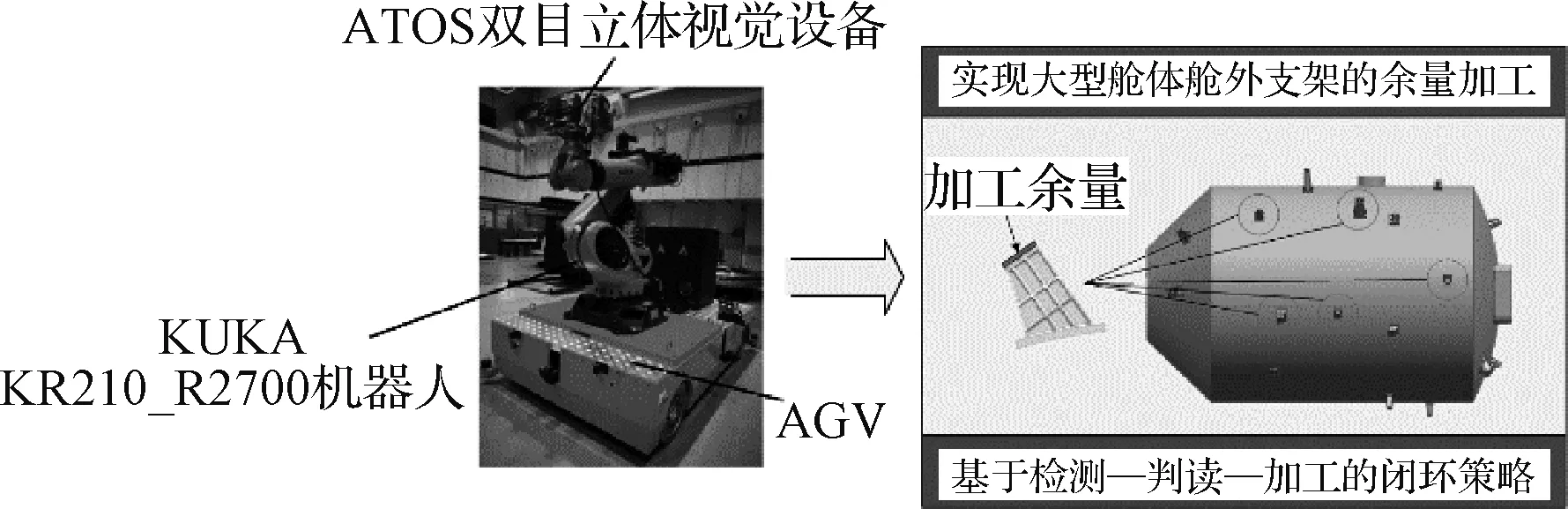
图1 可移动机器人检测系统示意图Fig.1 Illustration of mobile robot inspection system

采用可移动检测机器人对支架进行三维检测，系统主要组成部分如图1所示。执行机构采用KUKA机器人KR210_R2700由AGV进行搭载；视觉部分采用双目立体视觉设备，中心投影单元为光栅投影。针对待加工支架，提前规划好检测视点的位置信息及检测方向的姿态信息。由AGV搭载检测机器人到达指定站位，机器人携带视觉末端到达检测视点实现对支架的三维检测。

2 工作区域划分

针对航天器大型舱体的舱外支架三维检测任务，由于工作空间范围大、检测对象数量多，需要首先对可移动机器人的工作区域进行初步划分。分别从舱体轴向和舱体径向划分工作区域。

2.1 舱体轴向区域划分

舱体轴向区域的划分采用分布式的站位规划策略，基于机器人的工作空间和待检测对象结构尺寸范围约束，工作区域的划分应遵循以下原则：

1)尽可能多的支架要包含在工作区域范围内。

2)在保证检测任务能够完成的前提下，工作区域的数量尽可能少。

3)为避免机器人在工作空间极限位置附近运动，相邻工作区域需保证一定的重叠率。

4)重叠区域内的支架应归属于距离工作区域中心近的区域。

工作区域划分问题是一个典型的约束满足问题(Constraint satisfaction problem, CSP)，图2为检测场景布局示意图。定义舱体柱段支架检测视点范围长度为L，工作区域数量为N，相邻工作区域最小重叠距离为ε，实际重叠距离为Δd，求取符合条件的Nmin。

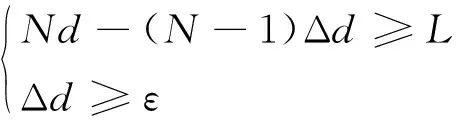
(1)

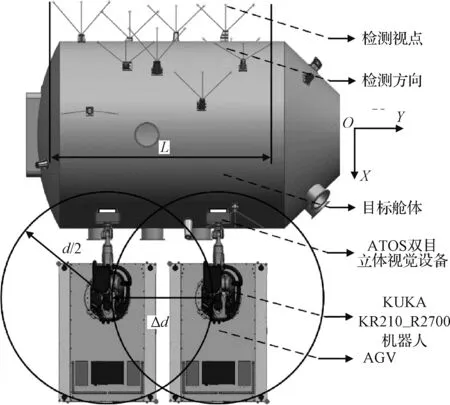
图2 轴向工作区域划分示意图Fig.2 Illustration of axial working area division

进一步，基于轴向区域划分需要对检测视点进行分组，确定对应工作区域内的视点。整舱基坐标系固定在舱体端面，定义舱体轴线方向为Y，竖直方向为Z。第1个轴向检测区域中心坐标为S0(x0，y0，z0)，第N个轴向检测区域中心坐标SN(N=0,1,2,…,n-1)为：

(xN,yN,zN)=(x0,y0+(N-1)(d-Δd),z0)

(2)

判断机器人检测视点Vi(xvi，yvi，zvi)所属轴向检测区域：

yvi-y0/(d-Δd)∈(N,N+1)

(3)

则Vi(xvi，yvi，zvi)∈SN。

2.2 舱体径向区域划分

对于六自由度串联机器人，一般情况下前三自由度可以使得机器人末端执行器到达工作空间中的指定位置，对于末端执行器的姿态调整主要由后三个自由度决定。机器人DH运动学模型简化如图3所示，其中A2轴,A3轴的转角分别定义为θ2,θ3，因此机器人工作空间X向的最大距离为D：

D=a1+a2×cosθ2min+d4×cosθ3min

(4)

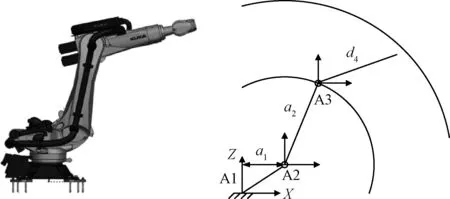
图3 机器人结构模型简化图Fig.3 Simplified model of robot structure

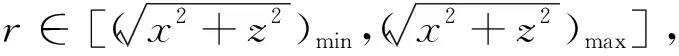
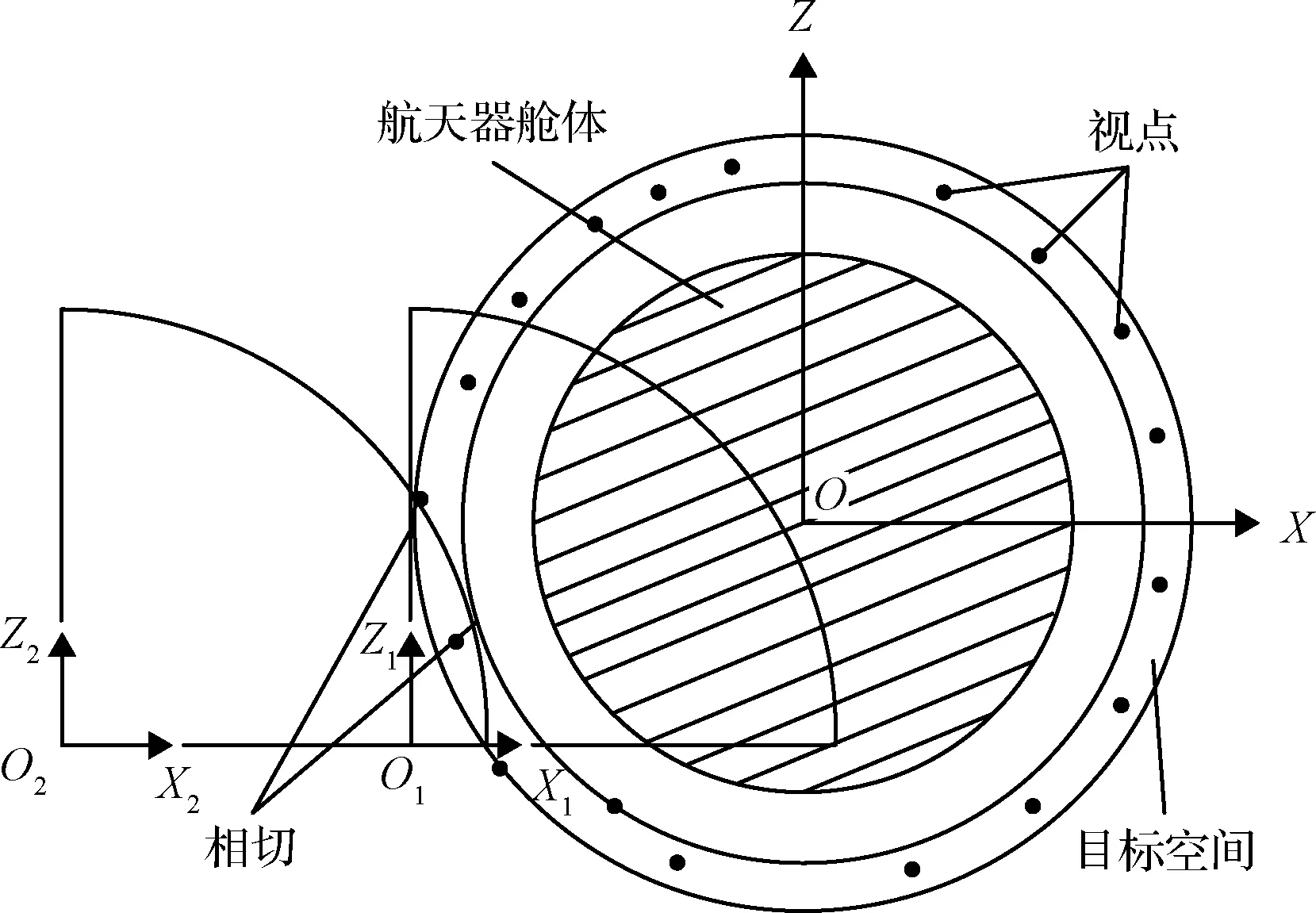
图4 径向工作区域划分示意图Fig.4 Illustration of radial working area division

基于给定机器人和舱体的数学模型，建立相互约束关系，初步确定沿舱体径向可移动检测机器人工作区域。整舱基坐标系的原点距离地面高度为H；径向最近处机器人基坐标系原点在整舱基坐标系中的位置为(Xmin，Zmin)，最远处位置为(Xmax，Zmax)且机器人基坐标系原点距离地面高度为h；检测视点所处的目标空间范围rmin≤r≤rmax，由此：

(5)

3 站位优化

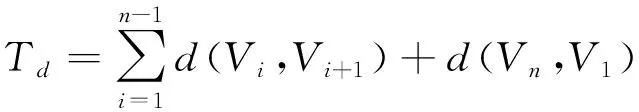
1)对固定站位下机器人工作区域内的n个视点进行编码表示。

2)以N个数量个体为种群并初始化。

3)建立适应度函数模型：

(6)

式中:v1,v2, …,vn表示一个采用整数编码的染色体，Dvivj表示视点vi与vj之间的欧几里得距离。

4)以概率P选择个体到新种群中。

5)对种群进行交叉、变异、进化、逆转操作。

6)循环操作，判断是否满足设定的最大遗传代数M，如果不满足则重新计算适应度函数，否则结束，遗传操作终止。

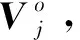
(7)

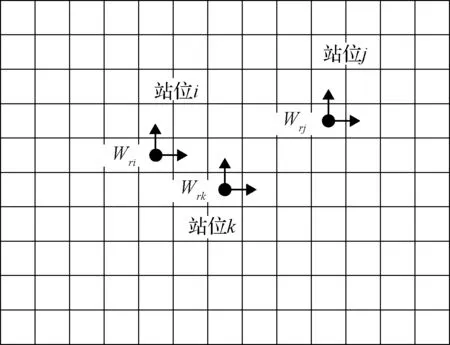
图5 工作区域离散化Fig.5 Working area discretization

遍历工作区域内的所有离散站位，基于机器人逆运动学求解对应各个站位机器人各关节角度值。串联机械臂的逆运动学问题是在给定末端相对于基座的位置和姿态，以及所有连杆集合参数的情况下，求取所有关节的位置信息。一般情况下，机器人的末端法兰盘中心相对于其基坐标系的姿态转换矩阵如下所示：

(8)

对式(8)进行矩阵逆变换可以得到：

(9)

令：

(10)

(11)

等式两边对应系数相等，则有：

(12)

1)θ1的求取

联立k4第3行与q4第3行,可得：

d6(axSθ1-ayCθ1)-pxSθ1+pyCθ1=0

(13)

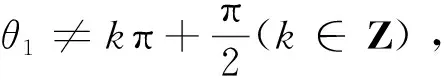
(14)

求得：

(15)

2)θ3的求取

联立k4和q4的第1行和第2行元素可得方程组如下：

(16)

式中:θ2和θ3为未知项，联立方程消去θ2，得θ3为：

(17)

其中,

(18)

3)θ2的求取

将θ1,θ3的值代入式(16)可得θ2：

(19)

其中,

(20)

4)θ5的求取

联立k3和q3的第1行和第2行元素可得方程组如下：

(21)

式中:θ4和θ5为未知项，联立方程消去θ4，得θ5为：

θ5=2kπ±arccos[azC(θ2+θ3)+

(axCθ1+aySθ1)S(θ2+θ3)]

(22)

5)θ4的求取

将θ5的值代入式(21)可得θ4：

(23)

6)θ6的求取

由k2和q2的第3行元素相等可得θ6：

(24)

由此，可以求解出机器人各个关节的转角。机器人的可达性验证必须满足两个条件：

(1)机器人逆运动学有解；

(2)各个关节转角的解必须满足机器人各个轴的限位。

因此，通过机器人逆运动学求解及约束条件的判断，可以得到满足机器人可达性的优化站位。

一般来说，在机器人的使用过程中，为了保证安全性和效率，需尽量保证机器人运动幅度尽可能小，即机器人各个关节角度变化值的方差尽可能小。假设视点的个数为k,θi表示第i轴转动的角度，σj表示第j轴角度变化的方差，因此，机器人各轴角度变化方差计算式如下所示：

(25)

由于机器人各个关节在运动过程中会产生关节转角误差，低序列的关节转角误差由于机器人运动学关系会累积到机器人末端，对机器人的绝对定位精度产生较大影响，高序列的关节转角误差由于运动学传递过程较少，对末端绝对定位精度影响较小。因此，在考虑机器人关节方差的情况下，从运动精度方面考虑，希望在机器人运动过程中，尽可能运动后几个关节。因此，对计算完成的关节方差进行加权处理，加权系数ki随着机器人关节序号的增大而降低。构造优化函数：

(26)

最终，选择优化函数值最小对应的机器人站位为最优站位。

4 算例验证

以试验大型密封舱体舱外支架检测为例，不考虑舱体锥段支架检测任务，舱体柱段长度为5000 mm，直径为4380 mm，检测视点沿舱体轴向分布范围是5500 mm，机器人选用KUKA KR210_R2700，安装在AGV上。系统布局如图6所示。

图6 系统仿真布局Fig.6 System simulation layout

首先进行工作区域的划分。针对舱体轴向区域，KUKA机器人KR210_R2700沿舱体轴向最大工作空间范围为5294 mm，考虑到末端位姿约束实际工作空间范围可能更小。因此，定义机器人工作空间范围d=5000 mm，令最小重叠距离ε=2000 mm，根据式(1)最终求得最少检测区域数量Nmin=2。然后，进行舱体径向区域划分。舱体坐标系原点与机器人基坐标系原点在y方向的高度差为1638 mm。基于检测视点空间坐标确定目标空间范围r∈[4640 mm, 5040 mm]，由式(5)可得径向最小距离为4640 mm，径向最大距离为7150 mm，式中机器人DH参数以理论参数计算，机器人关节2和关节3的转角范围分别为θ2∈[-5°,-140°]和θ3∈[-120°, 155°]。由此完成了多站位工作区域的划分，且划分策略考虑了实际AGV运动平面的两自由度。与之相对比的，多数研究者仅仅针对单站位工作区域的站位优化问题进行研究，即使考虑了多站位的情况(如文献[8]和文献[10])，仅仅是针对导轨式机器人单自由度方向上的工作区域划分，并不适用于基于AGV的可移动机器人的多站位工作区域划分。

以图6所对应的工作区域为例，针对检测路径规划之前27个检测视点，随机生成一个检测序列，检测视点间的欧几里得距离为29.789 m。基于遗传算法定义初始种群大小为80，最大遗传代数Gmax=300，交叉概率Pc=0.9，变异概率Pm=0.05，迭代优化后的检测路径视点间的欧几里得距离为8.981 m。在MATLAB中编写算法程序，运行结果如图7～图8所示。图7表示随着遗传代数的增加，检测视点之间欧几里得距离的收敛情况，可以看出随着遗传代数的增加，不断有新的检测序列使得视点间总的欧几里得距离更短，110代之后迭代曲线基本收敛。

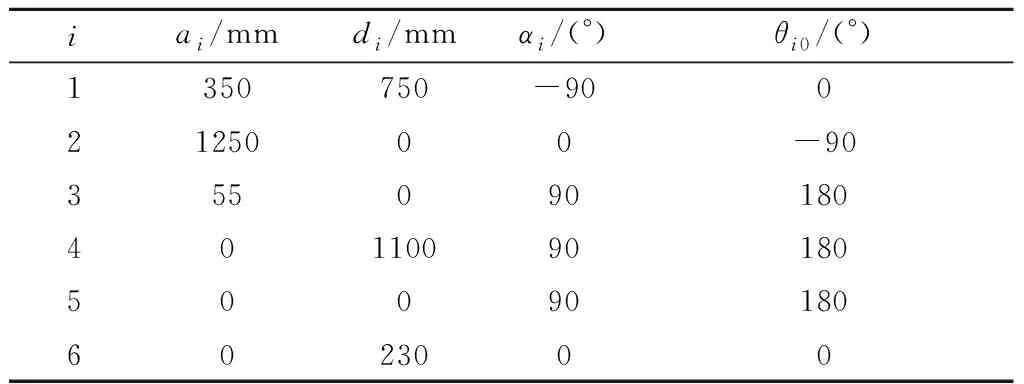
表1 理论DH参数Table 1 Theoretical DH parameters

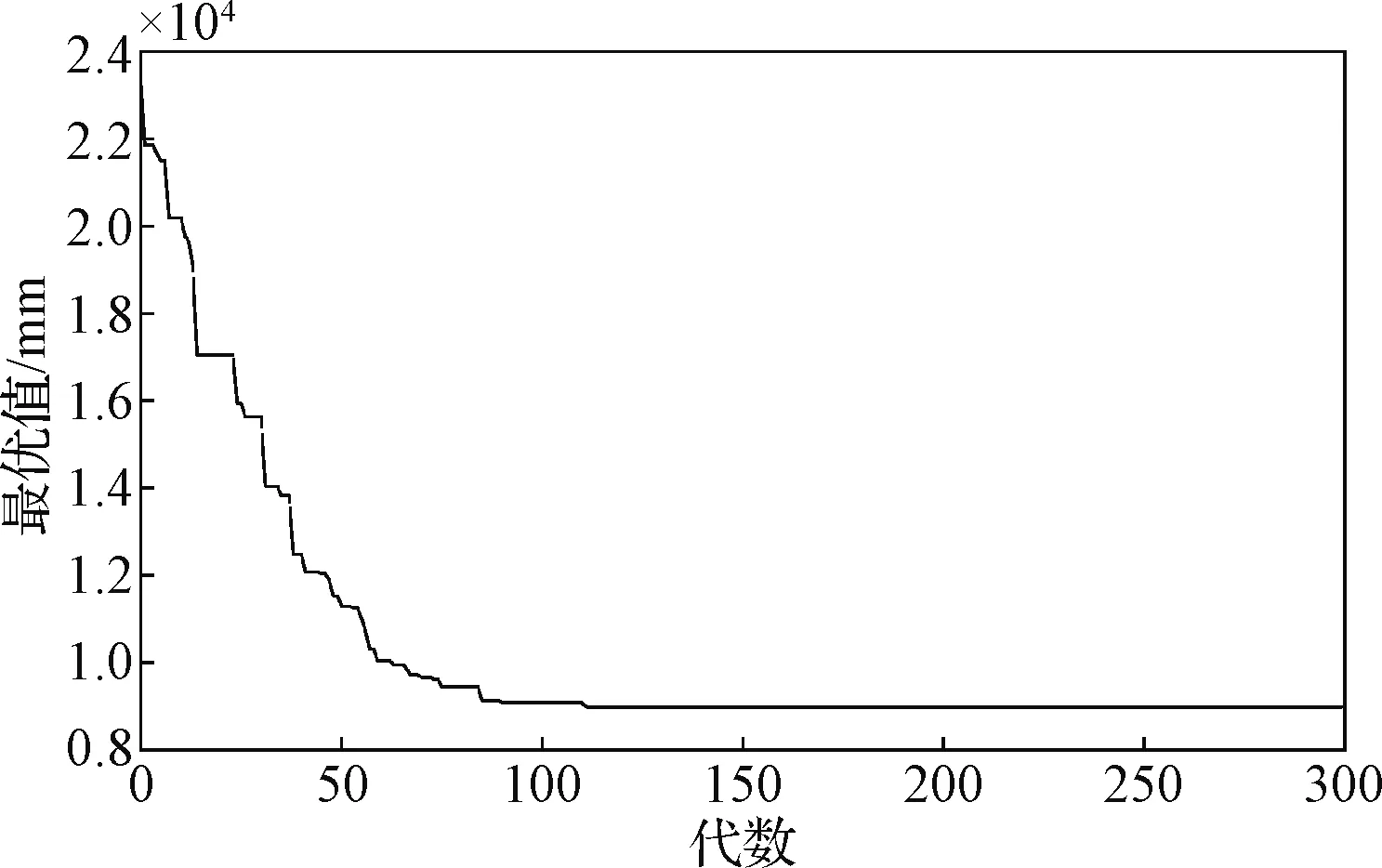
图7 迭代收敛曲线Fig.7 Iteration convergence curve

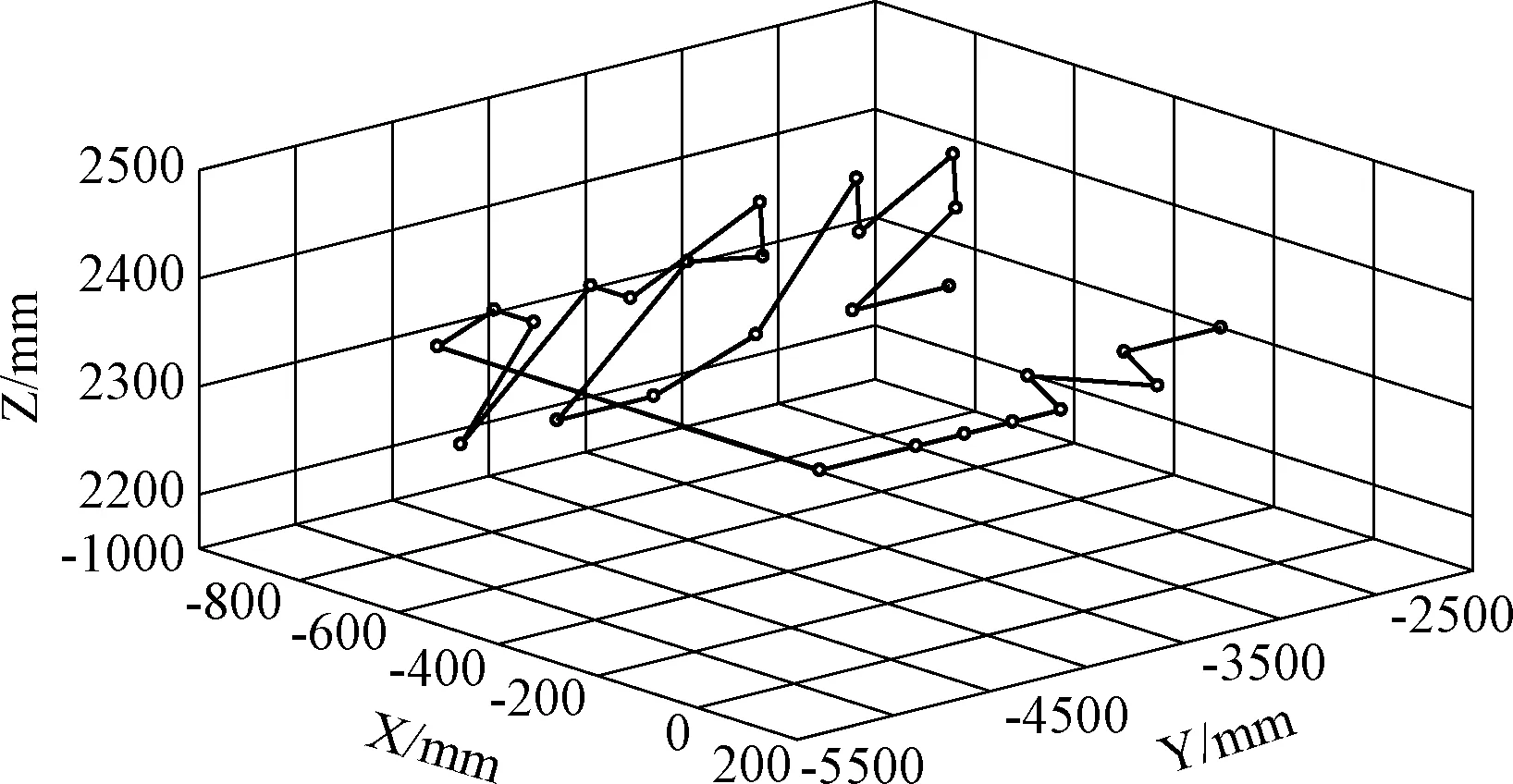
图8 规划后检测路径Fig.8 Inspection path after planning

进一步，基于机器人工作区域，离散成12×12的栅格区域，以每个栅格中心为机器人的基坐标系并将视点坐标转换到机器人各个基坐标系下，通过6R机器人逆运动学算法，判断是否存在实数解以及结果是否满足机器人关节限位的要求，解算结果如图9所示，图中空白区域即为满足要求的站位。针对27个目标检测视点，解算过程在2 min左右完成，且解算时间与栅格数量正相关。

图10为三个可行站位下所有检测视点对应的机器人各关节角度值变换曲线。为了获得最优站位，计算机器人各个关节角度变化方差，定义加权系数k1=0.35,k2=k3=0.25,k4=k5=k6=0.05，三个站位对应的优化函数值为D1=902.88,D2=1013.01,D3=1012.78。由此得到站位1为最优站位。至此，完成了对应工作区域内的站位优化。相较于其他算法的优化指标，基于机器人关节加权方差的优化策略以机器人运动过程的安全性、效率和精度为优化指标，结合机器人逆运动学实现对应工作区域内的可行站位进一步优化，算法直观，更适用于航空航天领域对可移动机器人应用过程中安全性、精度和效率的要求。

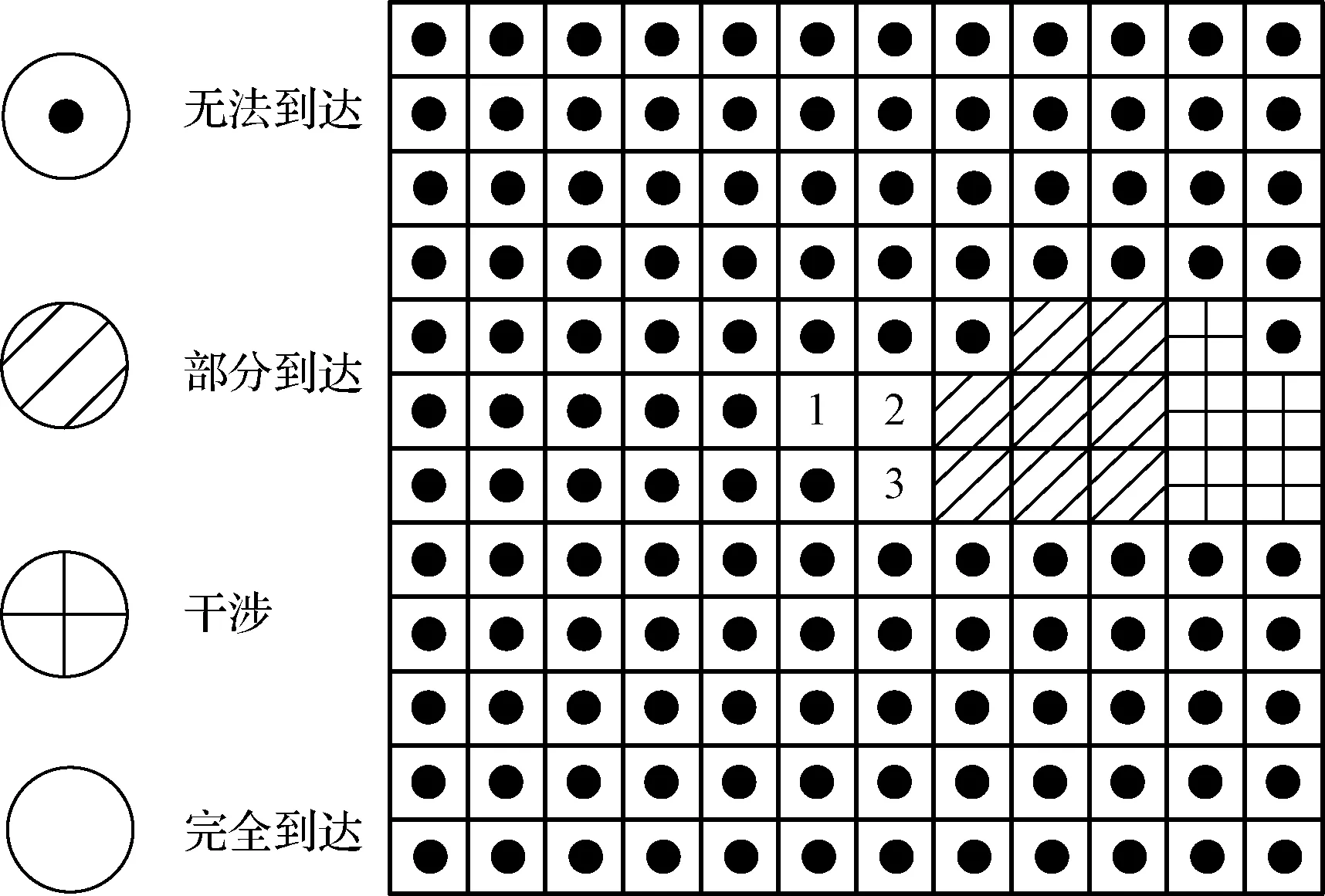
图9 工作区域可行站位解算结果Fig.9 Solution result of working area feasible base position

为了验证规划策略的正确性，在Process Simulate机器人仿真软件中搭建虚拟检测环境，将规划完成的最优站位坐标信息、27个检测视点位姿信息(包括视点位置信息和检测方向信息)、检测路径信息导入软件中。仿真过程采用与规划一致的机器人KUKA KR210_R2700，控制系统选择KRC4，机器人运动速度设定为0.2 m/s，加速度默认为最大加速度，运动形式为LIN。结果表明该优化站位能够满足所有检测视点的可达性要求，即机器人各关节角度均在约束范围内，机器人能够完成相应的检测任务。

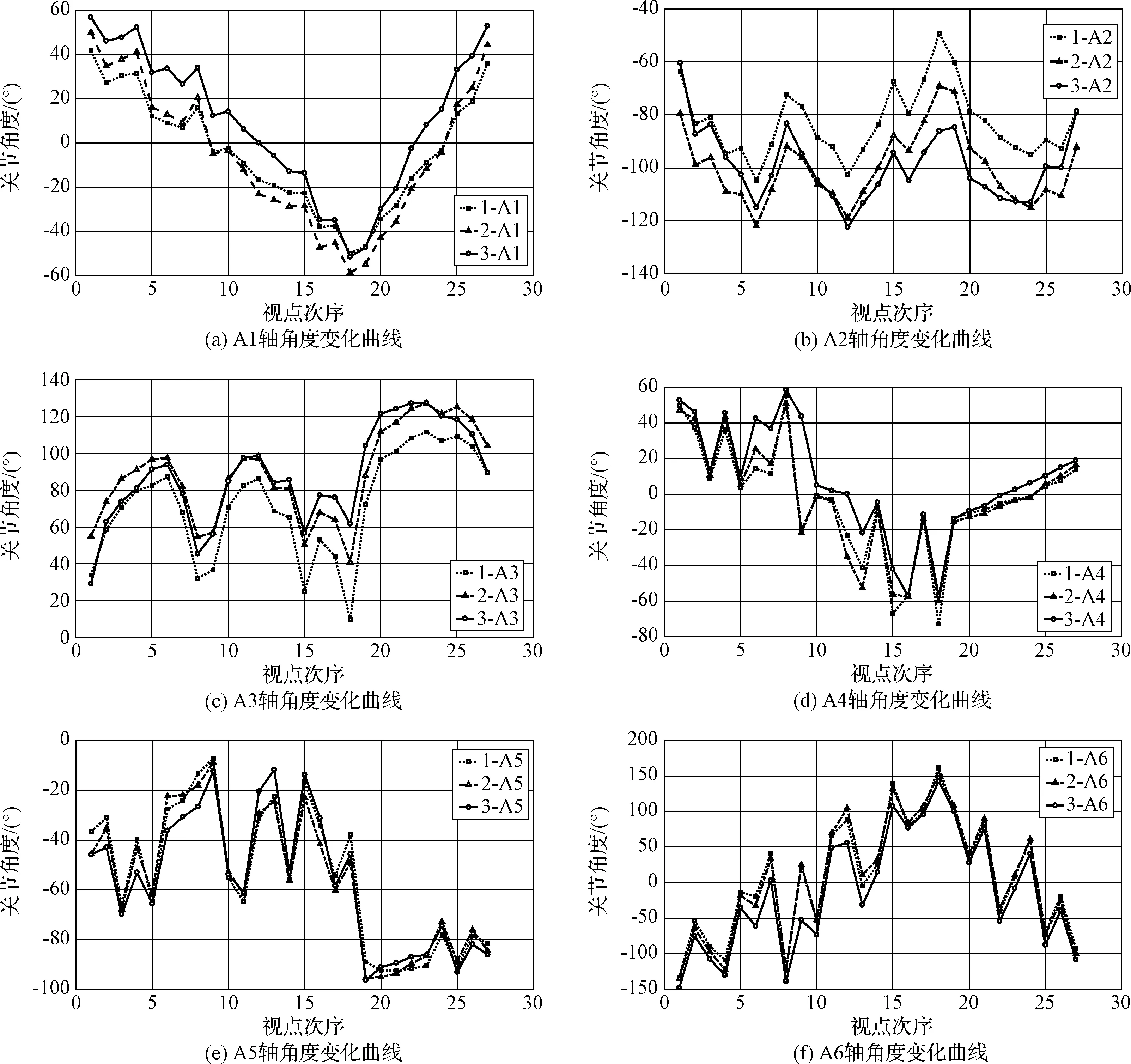
图10 可行站位对应各个关节角度变化情况Fig.10 Feasible base position corresponding to each joint angle change

5 结 论

本文针对大型航天器舱体舱外支架原位加工前三维检测过程中可移动检测机器人站位规划问题，提出了一种规划策略。基于机器人正运动学并构建检测环境数学模型，初步划分机器人工作区域。采用遗传算法确定检测次序并对工作区域离散化处理，结合机器人逆运动学计算工作区域内完全可达的站位。针对多组可行解，计算机器人运动过程中关节角度变化方差并加权处理，得到最优站位。本文的研究成果对类似基于可移动机器人的大尺寸对象制造过程中的站位规划具有良好的借鉴意义。