临近空间可变形滑翔飞行器轨迹优化与性能分析

陈铁彪，龚 旻，王洪波，王晨曦，许泽宇

(中国运载火箭技术研究院，北京 100076)

0 引 言

2017年5月，NASA官方报道了“自适应柔性后缘”项目的第二轮飞行试验，在“湾流”Ⅲ飞机上实现了飞行过程中的动态变形，标志着分布式柔性变形机翼技术进入了工程化应用研究阶段。在“人工智能”的技术牵引和智能化战争的需求牵引下，新一代飞行器不光要有智能决策的“聪明大脑”，也要有随需应变的“矫健身体”。随着智能飞行控制、随控气动布局设计、智能结构与智能材料等关键技术的蓬勃发展，智能变形飞行器迎来了新的发展机遇期。

临近空间滑翔飞行器是高超声速飞行器的典型代表，具有射程远、任务周期短、精度高、多目标覆盖和强突防的优势，但变化剧烈的飞行环境和大翼展的气动外形导致滑翔飞行器具有以下设计难点[1]：

1)大空域、宽速域下的环境适应性不足；

2)主动段大静不稳定度条件下控制系统设计困难；

3)海基发射系统和机载发射装置等尺寸约束难以满足。

引入变形技术可以有效解决以上设计约束和技术难点，同时具有以下优势：

1)通过变形提升滑翔飞行器的环境适应性，实现大空域、宽速域下的飞行器性能最优；

2)通过变形减小主动段静不稳定度，降低控制系统设计难度；

3)通过变形减小展向尺寸，便于运输和发射，提升飞行器的多平台适应性；

4)通过变形实现冗余姿态控制，增加控制系统的可靠性和容错能力；

5)通过变形拓展任务模式和弹道形式，提高导弹的突防能力；

6)通过自适应变形与智能决策的融合实现智能化作战。

在变形飞行器轨迹优化的理论研究方面，Florida大学在巡航、机动、陡降等不同的飞行阶段，通过气动外形的切换实现综合飞行性能最优[2]； Cornell大学研究了机身可变形的飞行器的轨迹优化问题[3]；温暖等[4]研究了一类变形飞行器的外形自主优化问题，通过强化学习使飞行器具有自主优化能力；李焕焕[5]研究了折叠翼飞行器的建模以及飞行方案的优化问题；张公平等[6]通过蒙特卡洛算法离线寻优，得到变形部件的自适应律；董朝阳等[7]研究了一类翼展可变飞行器的平滑切换线性变参数(LPV)H∞控制问题。目前，国内外关于变形飞行器的研究主要针对低速飞行器，而变形需求更大的临近空间滑翔飞行器的相关研究鲜有报道。本文将变形量作为轨迹优化问题的冗余控制变量，实现了变形控制与轨迹控制的一体化优化，同时得到了飞行过程中的最优变形律和最优控制律。

1 伸缩式可变形滑翔飞行器

本文基于典型翼身组合体滑翔飞行器，提出一种伸缩式可变形滑翔飞行器(Morphing glide vehicle，MGV)(见图1)，伸缩翼变形模式在工程上易于实现，且能够在空间有限的情况下保证较大可用过载，改善操稳特性。

MGV由弹身和四个伸缩翼组成，为“- +”布局形式，飞行中可连续对称变形。为便于描述，定义伸缩翼完全收拢时的状态为“原外形”，一级伸缩翼(WL1，WR1)完全打开时的状态为“伸缩1外形”，一级伸缩翼(WL1，WR1)、二级伸缩翼(WL2，WR2)同时打开的状态为“伸缩2外形”。

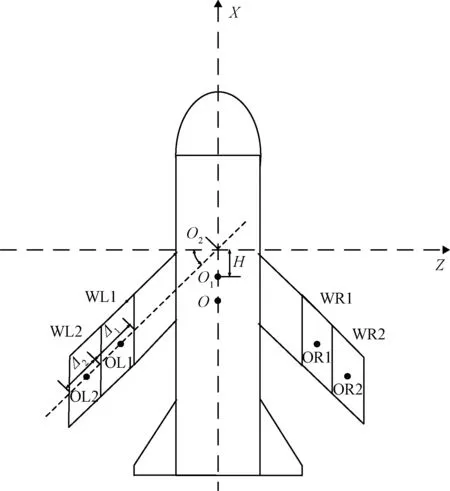
图1 可变形滑翔飞行器示意图Fig.1 Schematic diagram of morphing glide vehicle

MGV的变形量η作如下定义：

Δ1+Δ2=ΔL
η=1+ΔL/l

式中：Δ1为一级变形翼伸缩量，Δ2为二级变形翼伸缩量，l为变形翼长度。通过以上定义可知，变形量η=1时对应“原外形”；η=2时对应“伸缩1外形”；η=3时对应“伸缩2外形”；3>η>2, 2>η>1时，为三种外形间的过渡状态。

2 MGV冗余控制变量轨迹优化模型的建立

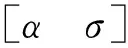
1)轨迹优化中仅考虑飞行器气动特性的变化，忽略由于质量特性变化而引起的附加力；

2)忽略变形引起的非定常气动特性；

3)不考虑地球自转和地球扁率影响；

4)采用瞬时平衡假设，忽略控制回路的动态特性，假定需用攻角、倾斜角和变形量可以通过变形控制系统和飞行控制系统实时获得；

5)本文主要分析变形技术对于飞行器气动性能及战技指标的提升，不考虑变形机构带来的附加质量影响和变形引起的缝隙防隔热问题。

2.1 动力学模型

滑翔飞行器质心动力学和运动学方程如下[8]:

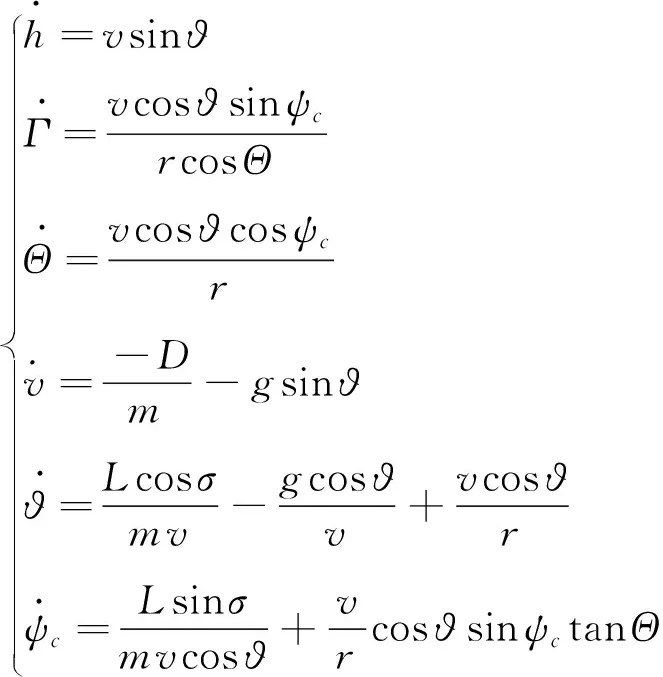
(1)

式中：ϑ为轨迹倾角，ψc为轨迹偏角，Θ为纬度，Γ为经度，σ为倾斜角。

2.2 气动模型

与固定外形飞行器不同，MGV的气动模型是攻角α、马赫数Ma和变形量η三者的函数。利用Fluent软件计算“原外形”、“伸缩1外形”和“伸缩2外形”三种外形在各种工况下的升力系数和阻力系数，进而采用式(2)所示的拟合函数分别对三种外形的气动数据进行拟合。用确定系数(R-S)表征拟合程度的好坏，R-S的取值范围是[0,1]，越接近1，表明拟合程度越好。如表1所示，三种外形拟合的确定系数均在0.92以上，拟合效果较好。

(2)

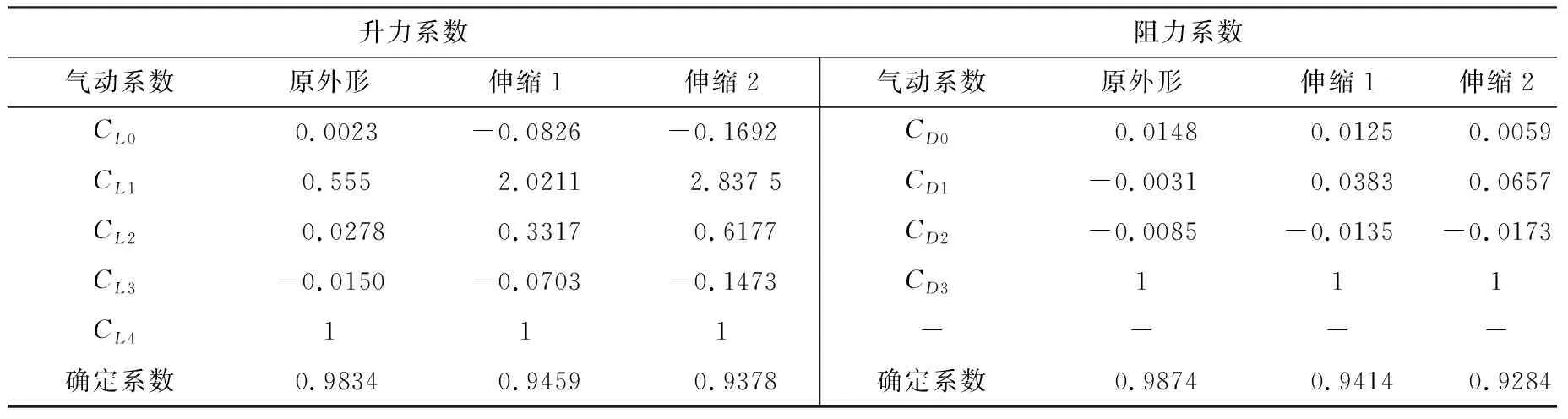
表1 拟合气动系数Table 1 Fitting aerodynamic coefficients

固定外形滑翔飞行器的拟合气动系数为常数，而MGV的拟合气动系数是变形量η的函数，将上述气动系数对变形量进行插值，进而得到了与攻角、倾斜角和变形量三者相关的MGV气动模型，供轨迹优化使用。

2.3 约束模型

滑翔飞行器恶劣的飞行环境带来比传统飞行器更为严苛和多样的轨迹优化约束，文献[9]详细总结了滑翔飞行器受到的各种约束(见图2)，如初始条件约束、终端条件约束、路径约束和控制约束，各个约束又同时受姿控、载荷、制导和突防等多专业的影响。

本文主要考虑热流密度约束、过载约束、动压约束、控制量约束、初始/终端约束和地理约束。

1)热流密度约束

为降低热防护系统的压力，需要对驻点热流密度进行限制，驻点热流密度的工程估算表达式为

(3)

式中：ρ为大气密度，v为飞行速度，kh,n和m为和飞行器相关的经验参数。

2)过载约束

为了保证高超声速飞行器的结构安全，需要考虑过载约束

(4)

式中：最大允许总过载Nmax主要取决于飞行器的结构强度和机载设备的可承受过载范围。

3)动压约束

为保证滑翔飞行器气动操纵面所产生的铰链力矩在特定的控制能力范围之内，同时受机体结构强度和飞行器表面防热材料性能约束，需要对滑翔段的动压提出限制

(5)

4)控制量约束

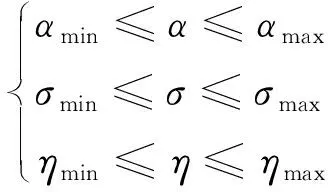
(6)

式中：α为攻角，σ为倾斜角，η为变形量。

5)终端约束

为了更好地转入末制导段，飞行器需要满足一定的终端约束条件

(7)

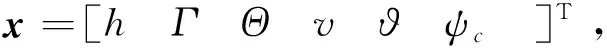
6)地理约束

地理约束主要指的是禁飞区约束，由于军事、政治等原因，执行特殊任务的滑翔飞行器需要回避一定的地理位置(敌对国防空阵地和本土重要城市等)。禁飞区可简化假设为一个无限高的圆柱，该圆柱在地面的投影为禁飞圆，圆心为禁飞中心，要求飞行器在地面的投影到禁飞中心之间的距离不能小于禁飞圆的半径

(8)

式中：Γi和Θi为第i个禁飞中心所在的经度和纬度,li为飞行器质心在地面的投影到禁飞中心之间的距离,di为第i个禁飞圆的直径,n为禁飞区的数目。

3 轨迹优化与性能分析

近年来，全局正交配点法——伪谱法发展迅速，由于其特殊的离散格式，提高了多项式近似的精度，采用较少的计算节点就能获得很高的计算精度，已经应用于X-33的轨迹优化和国际空间站的姿态机动[10-11]，实现了该方法的工程应用。

变形飞行器的环境适应性强，体现在大空域、宽速域范围内巡航能力(升阻比)和机动能力(可用过载)的提升，本文利用伪谱法分别对MGV和固定外形飞行器(即原外形)的滑翔段轨迹进行优化，定量分析MGV在射程覆盖、规避绕飞和末段打击三方面的性能收益，同时得到飞行过程中的最优变形律。

3.1 仿真参数

初始约束：

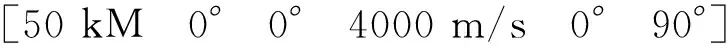
终端约束：

控制量约束：

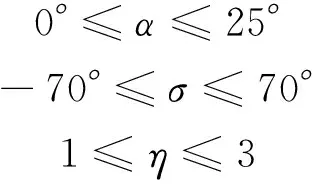
过程约束：

3.2 射程覆盖能力分析

3.2.1最大纵程轨迹

利用伪谱法优化时，目标函数选为J=maxΓf，优化结果如图3～8所示。

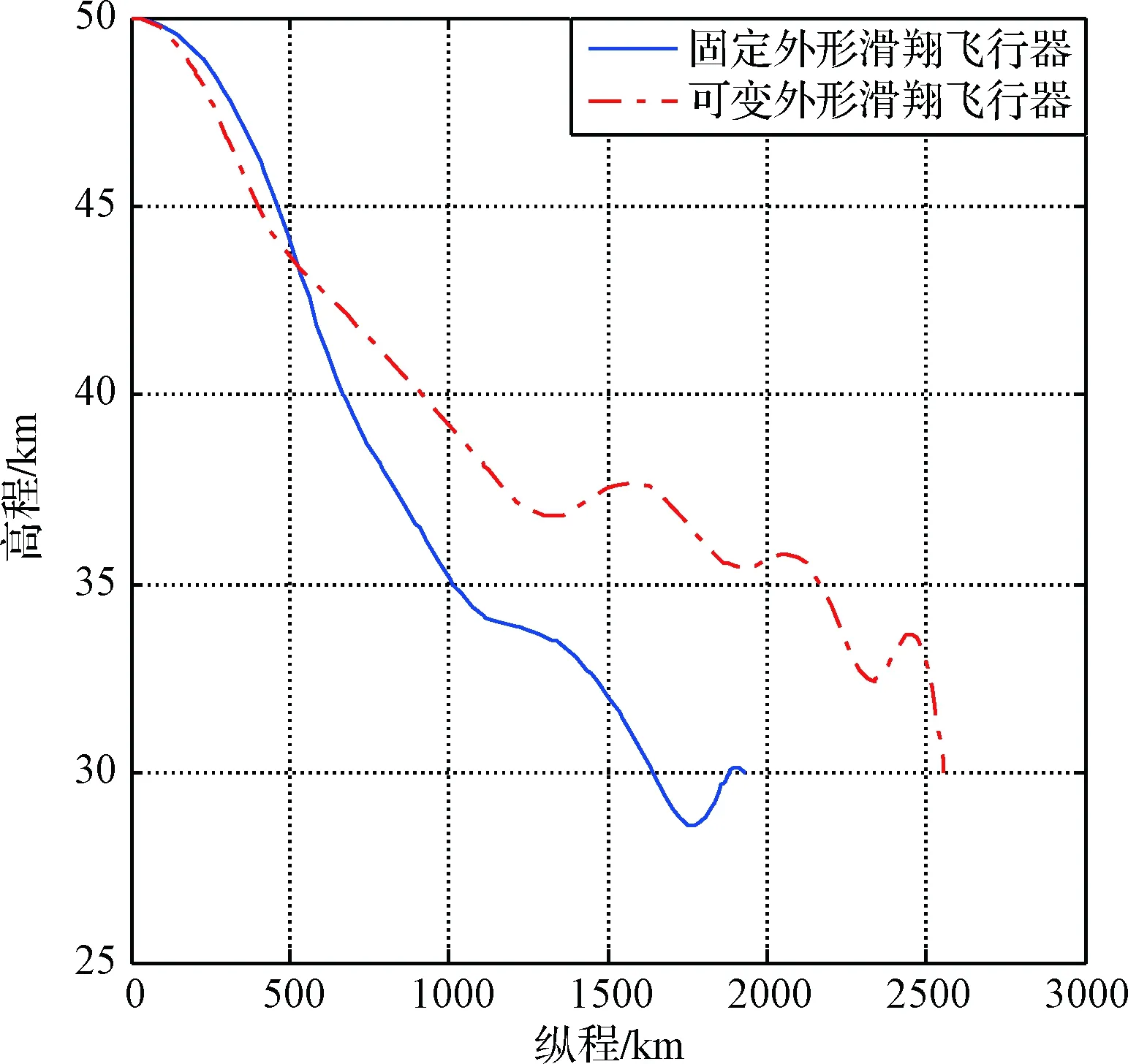
图3 最大纵程轨迹Fig.3 Maximum longitudinal trajectory

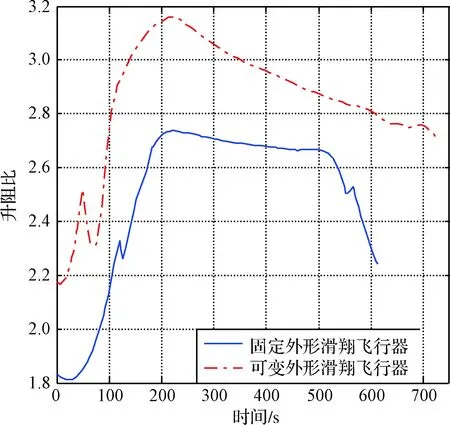
图4 升阻比变化曲线Fig.4 Lift resistance ratio curve

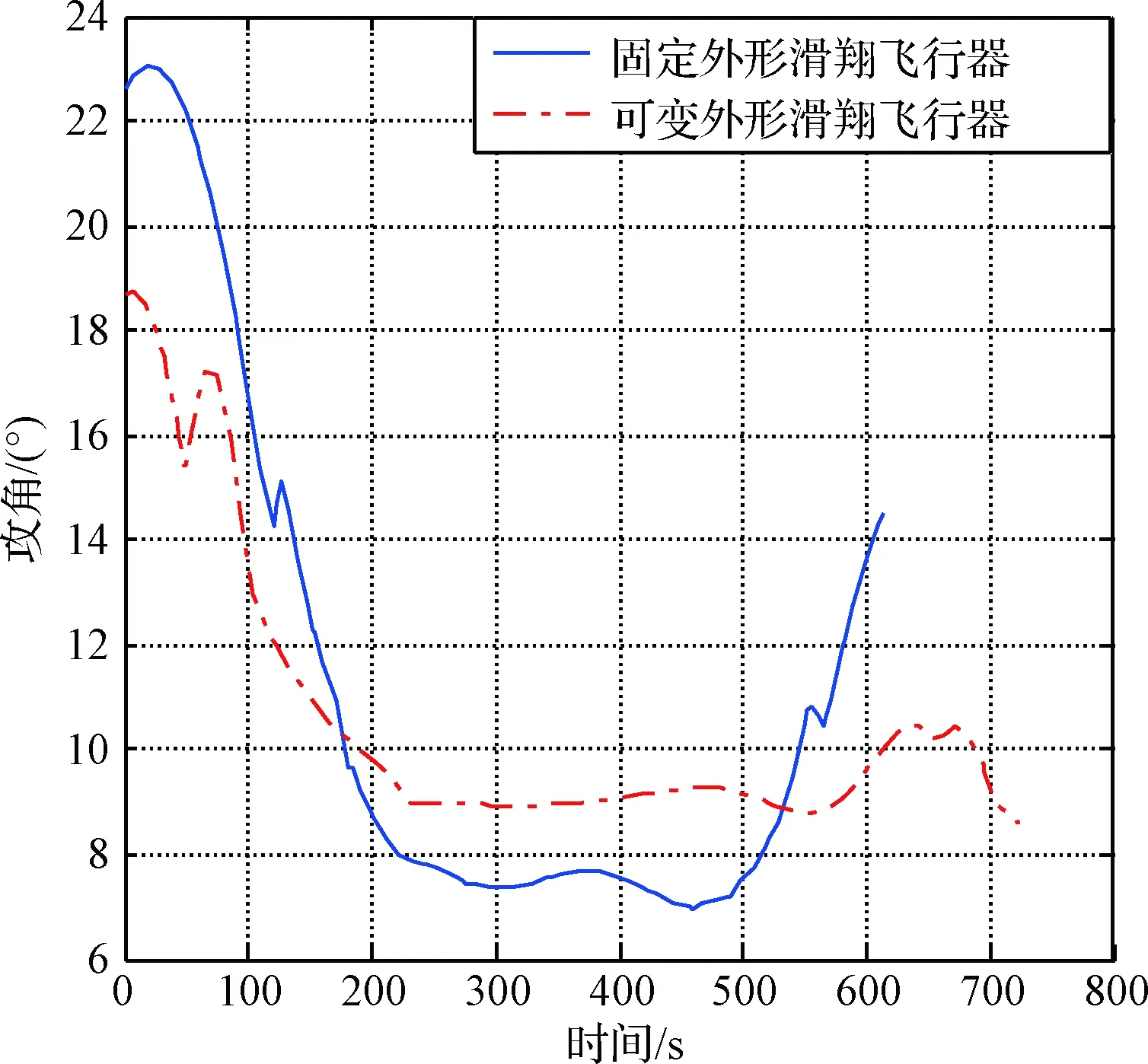
图5 攻角变化曲线Fig.5 Angle of attack curve

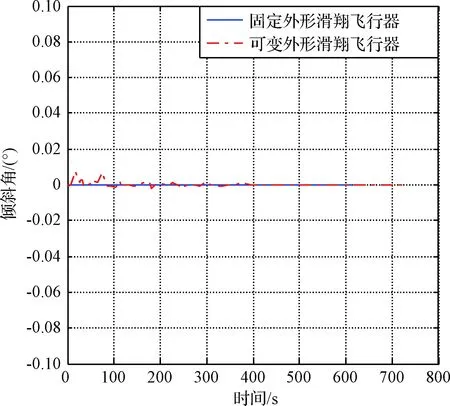
图6 倾斜角变化曲线Fig.6 Tilt angle curve

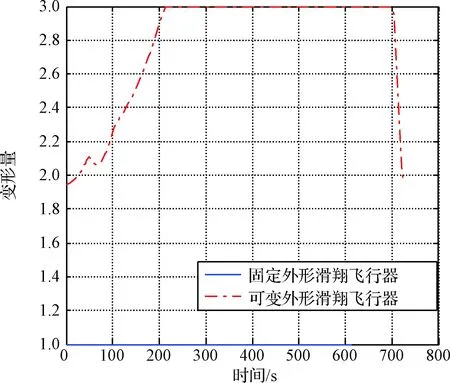
图7 变形量变化曲线Fig.7 Deformation curve

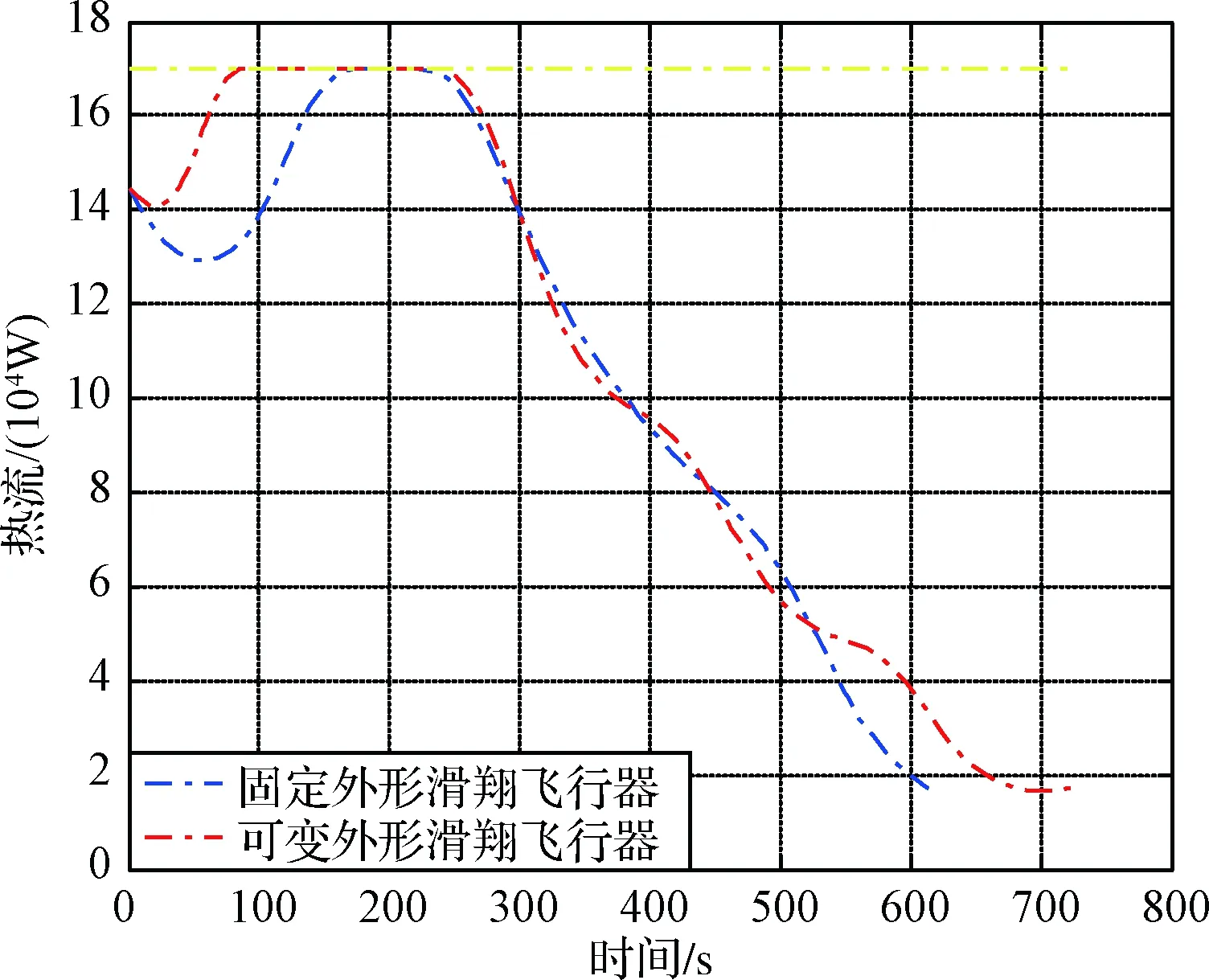
图8 热流密度变化曲线Fig.8 Heatflow density curve

通过分析轨迹优化结果可以看出：

1)如图3所示，MGV的最大射程为2272.6 km，相对于固定外形滑翔飞行器(1932.8 km)提升了17.6%。

2)如图4所示，MGV的升阻比在整个飞行阶段均高于固定外形滑翔飞行器，其环境适应性更强。

3)如图5、图8所示，滑翔段热流最大值出现在滑翔段初期。由于热流约束限制，固定外形滑翔飞行器采用大攻角将轨迹拉起，导致此段滑翔飞行的升阻比较低，能量损失较大。而MGV通过变形(伸缩翼伸展)获得足够的升力将轨迹拉起，避免了大攻角飞行带来的射程损失和严酷力热环境。在整个滑翔段，MGV的攻角变化范围较小，有利于滑翔增程和防隔热设计。

4)如图6所示，为获得最大射程，飞行器在整个飞行过程中的倾斜角几乎为零，无横向机动。

5)如图5～图7所示，轨迹优化结果同时得到了最优控制律和最优变形律。从变形量的优化结果可以看出，“伸缩1外形”是滑翔初始时刻的最优气动外形，随着速度的降低，最优气动外形对应的翼展逐渐增加，当马赫数下降到7以后时，“伸缩2外形”为最优气动外形。飞行过程中变形翼不需要反复伸缩，有利于变形技术在滑翔飞行器上的工程化实现。

3.2.2最大横程轨迹

最大横程轨迹可以评价飞行器的机动能力，机动能力越强飞行器的轨迹形式越丰富，突防能力、规避绕飞能力和目标控制能力都会相应提高。对于最大横程轨迹，目标函数选为J=maxΘf，优化结果如图9、图10所示。

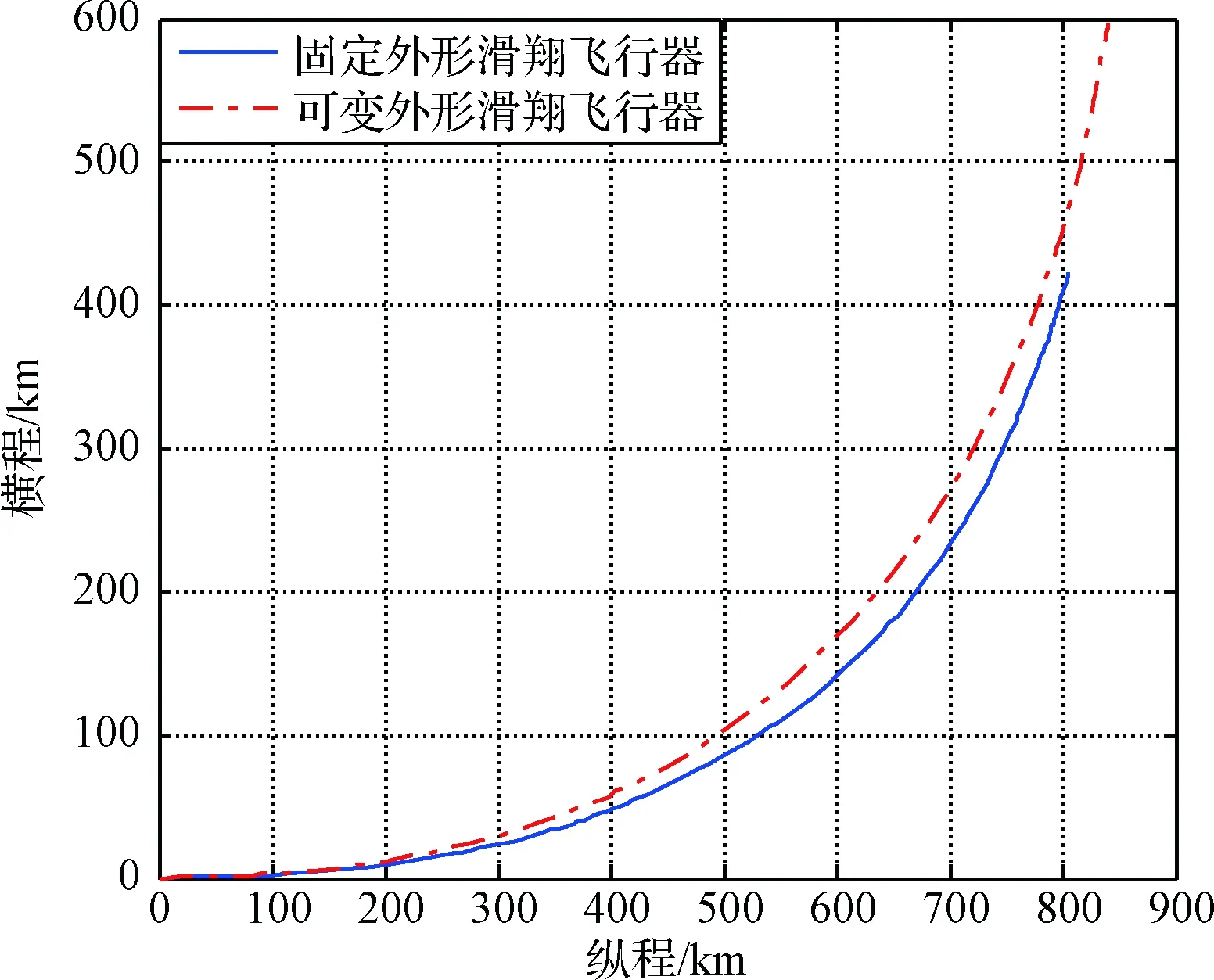
图9 最大横程轨迹Fig.9 The largest horizontal trajectory

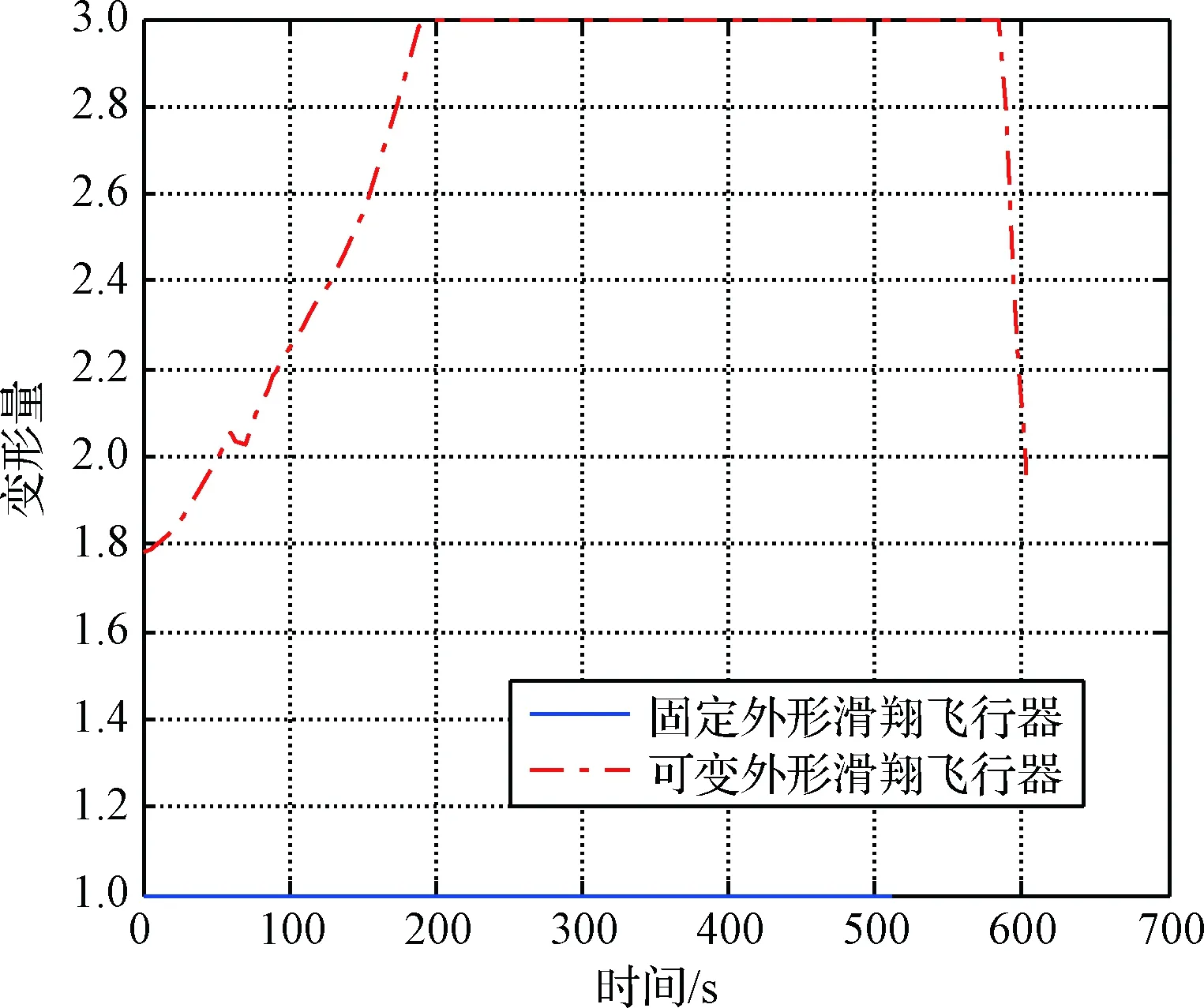
图10 变形量变化曲线Fig.10 Deformation curve

如图9所示，MGV的最大横程896.624 km，相对于原外形(635.1961 km)提升了41.6%，可见变形技术对于飞行器机动能力的提升是相当可观的；如图10所示，随着速度的降低，MGV的最优气动外形对应的翼展逐渐增加，当速度降到Ma6.65时采用“伸缩2外形”以获得最优的飞行性能。

3.2.3可达区域/起滑窗口

可达区域是指在某些约束条件下，飞行器在地球表面上的可达范围边界曲线，此曲线可通过若干组最优轨迹拟合得到。此区域的确定可为飞行任务规划提供有力支撑。

图11中外包络区域为MGV的可达区域，内包络区域为原外形滑翔飞行器的可达区域，通过计算可知，MGV的射程覆盖范围增加了95.3%。

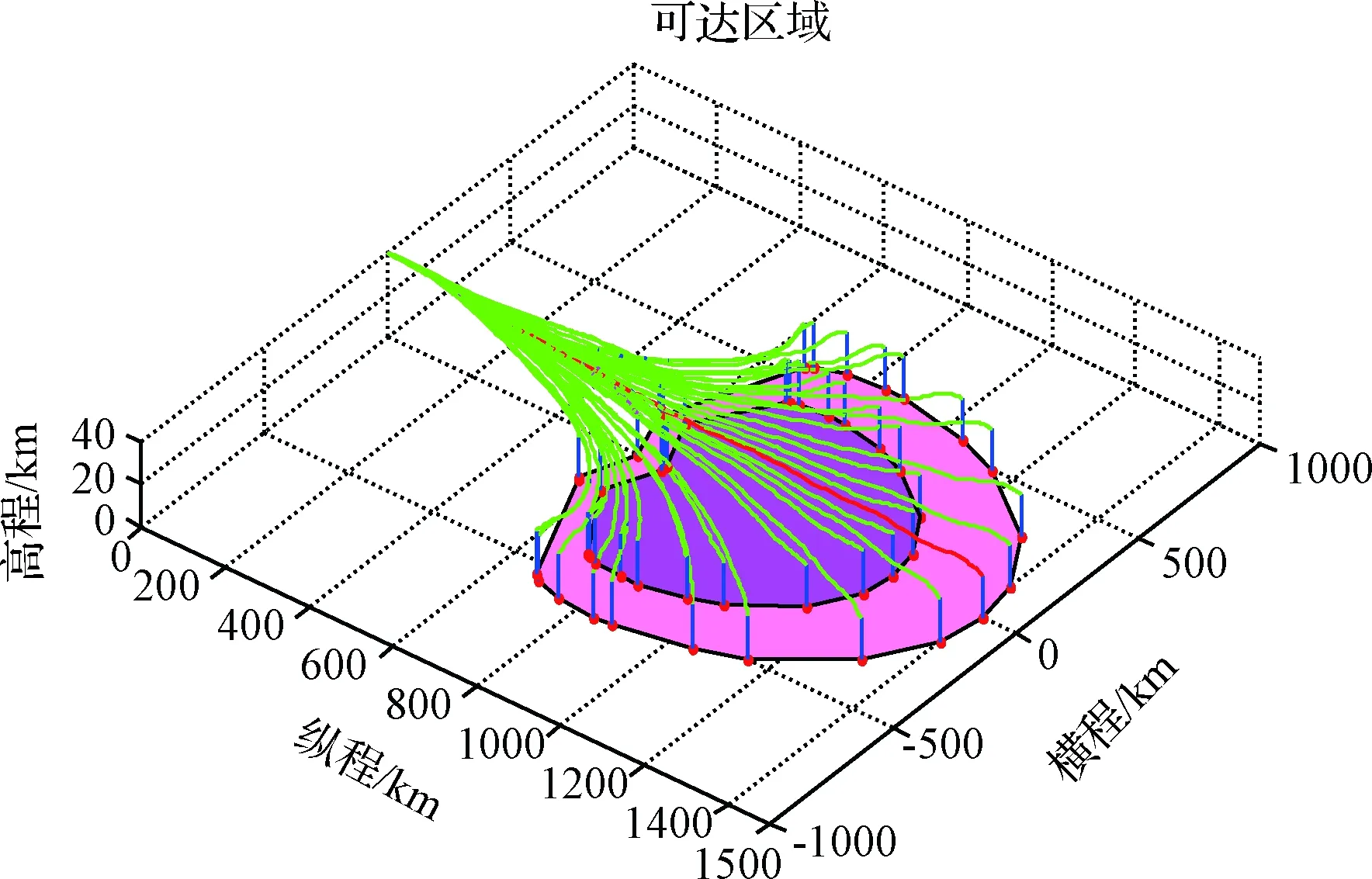
图11 可达区域Fig.11 Reachable area

起滑窗口是指满足某些约束条件下，飞行器能够到达目标点时，起滑点的最大包络曲线。起滑窗口与可达区域的本质是一样的，可以通过对可达区域轨迹包络进行坐标平移得到。可达区域/起滑窗口的扩大，表明MGV具有更强的射程覆盖能力，更强的火力封锁和纵深打击能力，同时投放窗口(机载)更加宽松，阵地部署(陆基)更加灵活。

3.3 规避绕飞能力分析

由于地缘政治限制和地面防空系统威胁，滑翔飞行器轨迹规划时要考虑禁飞区约束，利用其机动能力对禁飞区进行规避。下面分别设计两种地理约束下飞行器的最优轨迹。

3.3.1禁飞区约束下的最大纵程

假定距离起滑点(400 km，-100 km)处有一半径150 km的禁飞区；距离起滑点(700 km，100 km)处有一半径100 km的禁飞区。以最大纵程为优化目标，优化轨迹如图12所示。

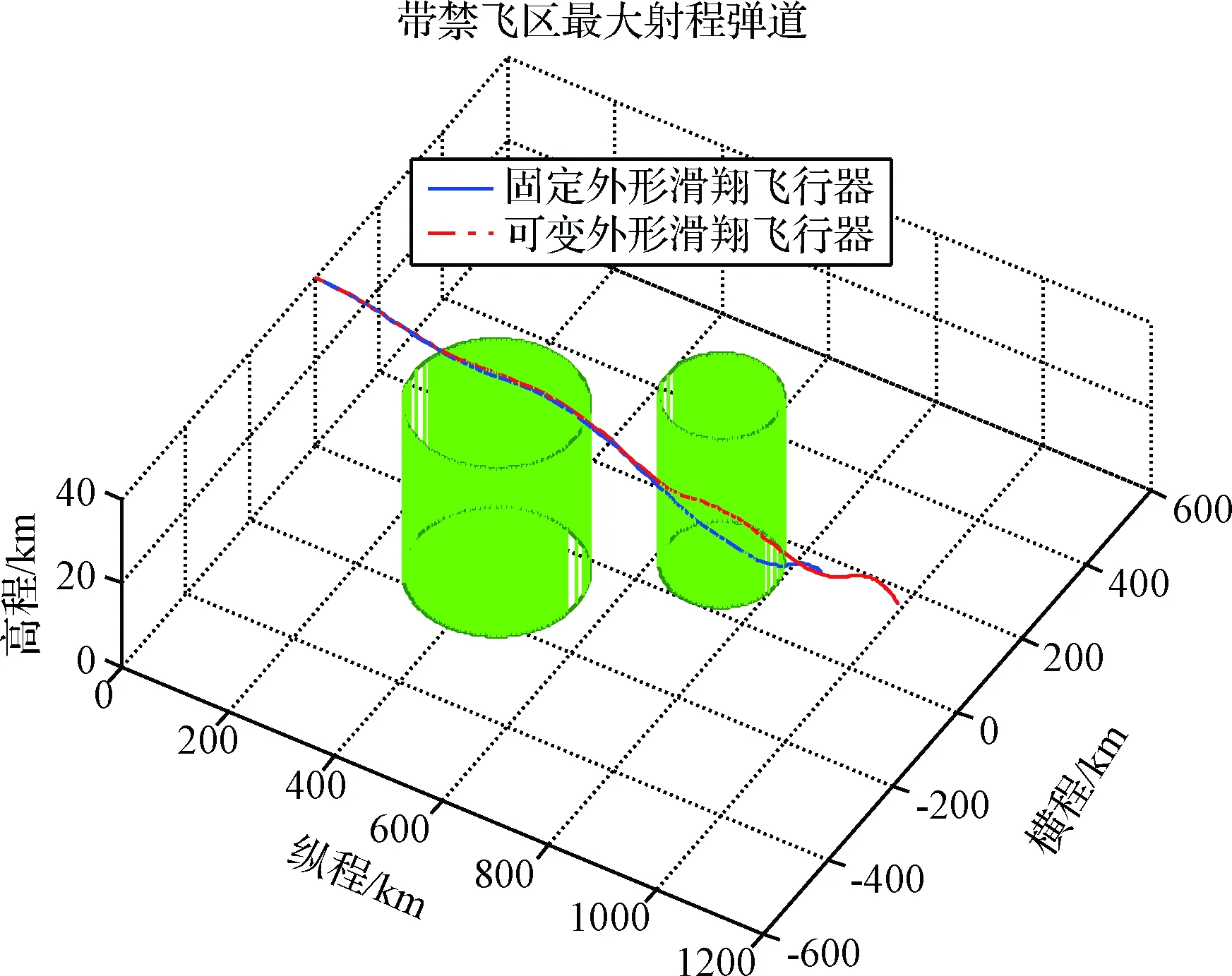
图12 带禁飞区的规避绕飞轨迹Fig.12 Flight path with a no-fly zone

从图12可以看出，两种滑翔飞行器均能规避禁飞区。为了获得最大射程，最优轨迹与禁飞区边界相切。绕飞后MGV仍能保持1100 km左右的射程，但是原外形飞行器射程下降为940 km左右。

3.3.2禁飞区约束下的覆盖“盲区”

假定距离起滑点(600 km，0 km)处有一半径100 km的敌方近程防空区。滑翔飞行器利用其机动能力可以绕过敌方近程防空区打击目标，体现出突防方面的优势，但受机动能力限制，势必存在部分区域因禁飞区存在而无法到达，这部分区域称为覆盖“盲区”。从轨迹优化结果可知(见图13)，MGV的机动能力更强，覆盖“盲区”缩小了37.5%，在突防任务中更有优势。

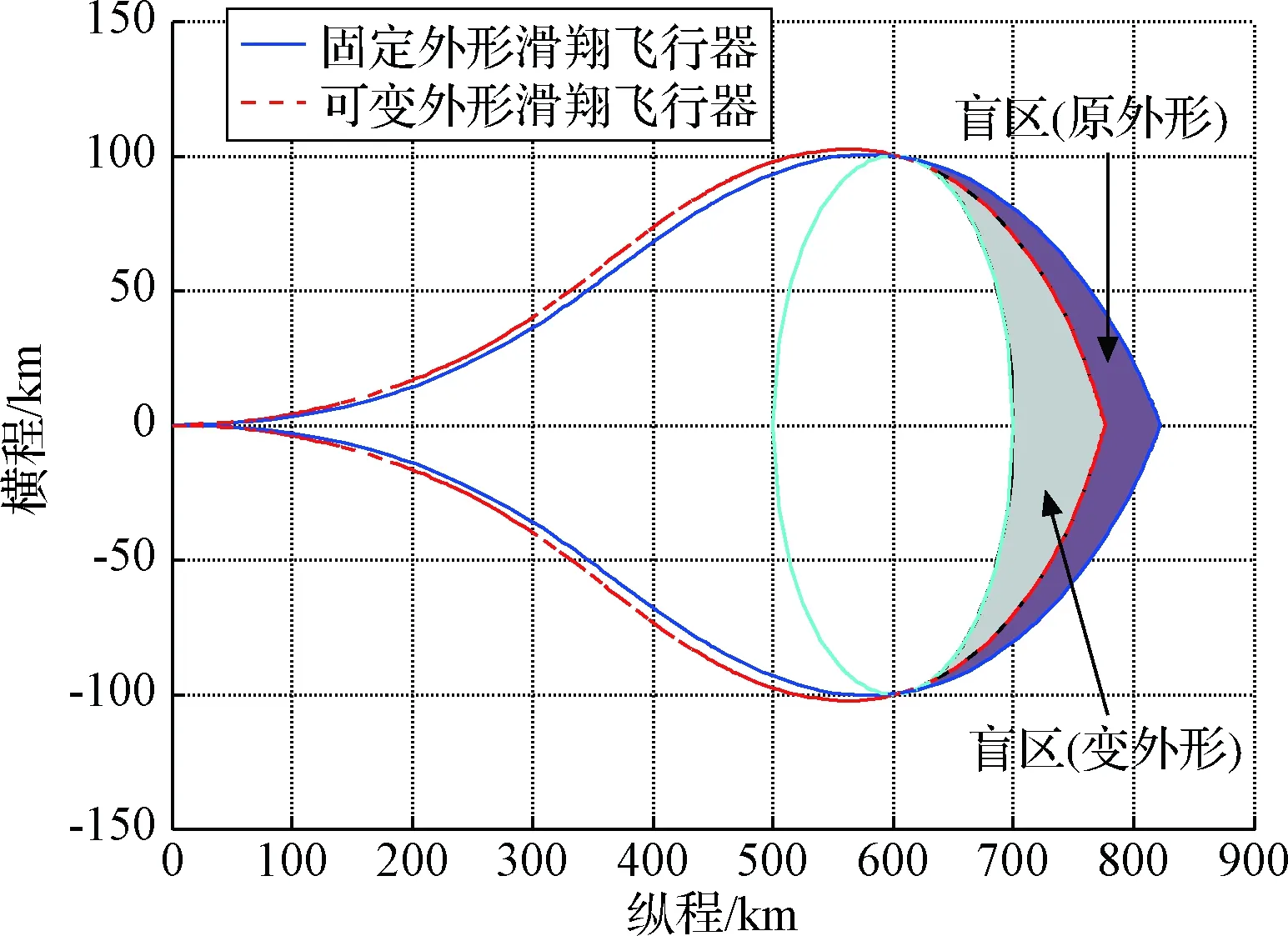
图13 敌近程防空导致的覆盖“盲区”Fig.13 Coverage blind zone

3.4 末段打击能力分析

3.4.1交接班能力分析

在打击确定目标时，受各种约束条件限制，飞行器的滑翔段与末制导段之间的交接点必须限制在一定范围内，这个位置范围称为“交接班窗口”，图14为滑翔段与末制导段的交接班窗口示意图。

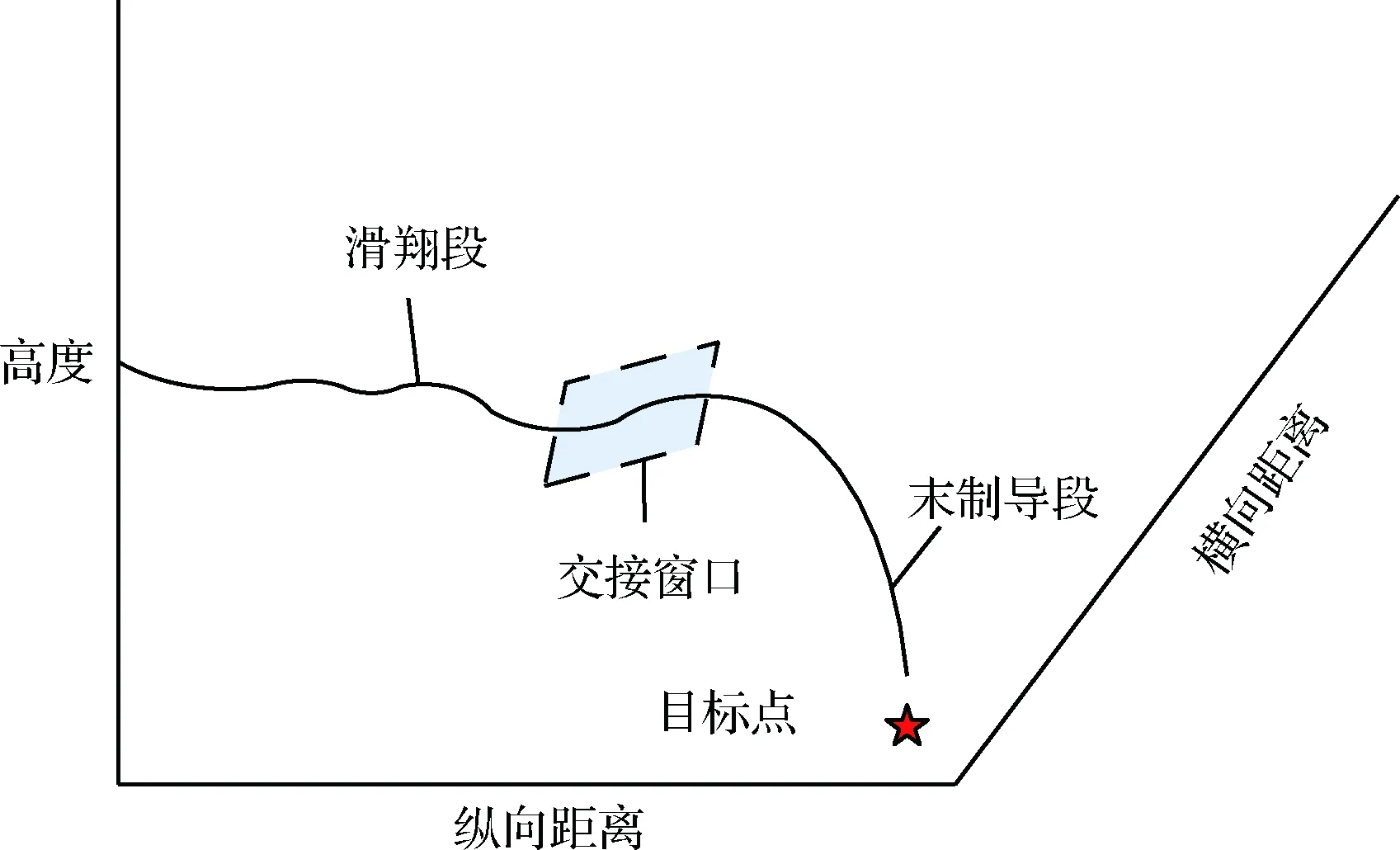
图14 交接班窗口示意图Fig.14 The window of handover

根据文献[8]，过载约束将影响飞行器的轨迹下压能力。较大的可用法向过载能够使飞行器快速地下压轨迹，末制导初始点可以选在距目标较近的位置，MGV可通过伸缩翼伸展获得足够的可用过载从而有效增大交接班窗口，有利于实现顺利交班和精确打击。

3.4.2轨迹下压能力分析

滑翔飞行器在攻击一些加固目标和地下深层目标时，往往需要进行高速灌顶打击。假设飞行器进入末段攻击的起始高度为30 km，初始速度1700 m/s，攻角调节范围在0°至25°之间，最大可用过载为10，以最小落地倾角为优化目标，分析可变形滑翔飞行器和固定外形滑翔飞行器的轨迹特点。

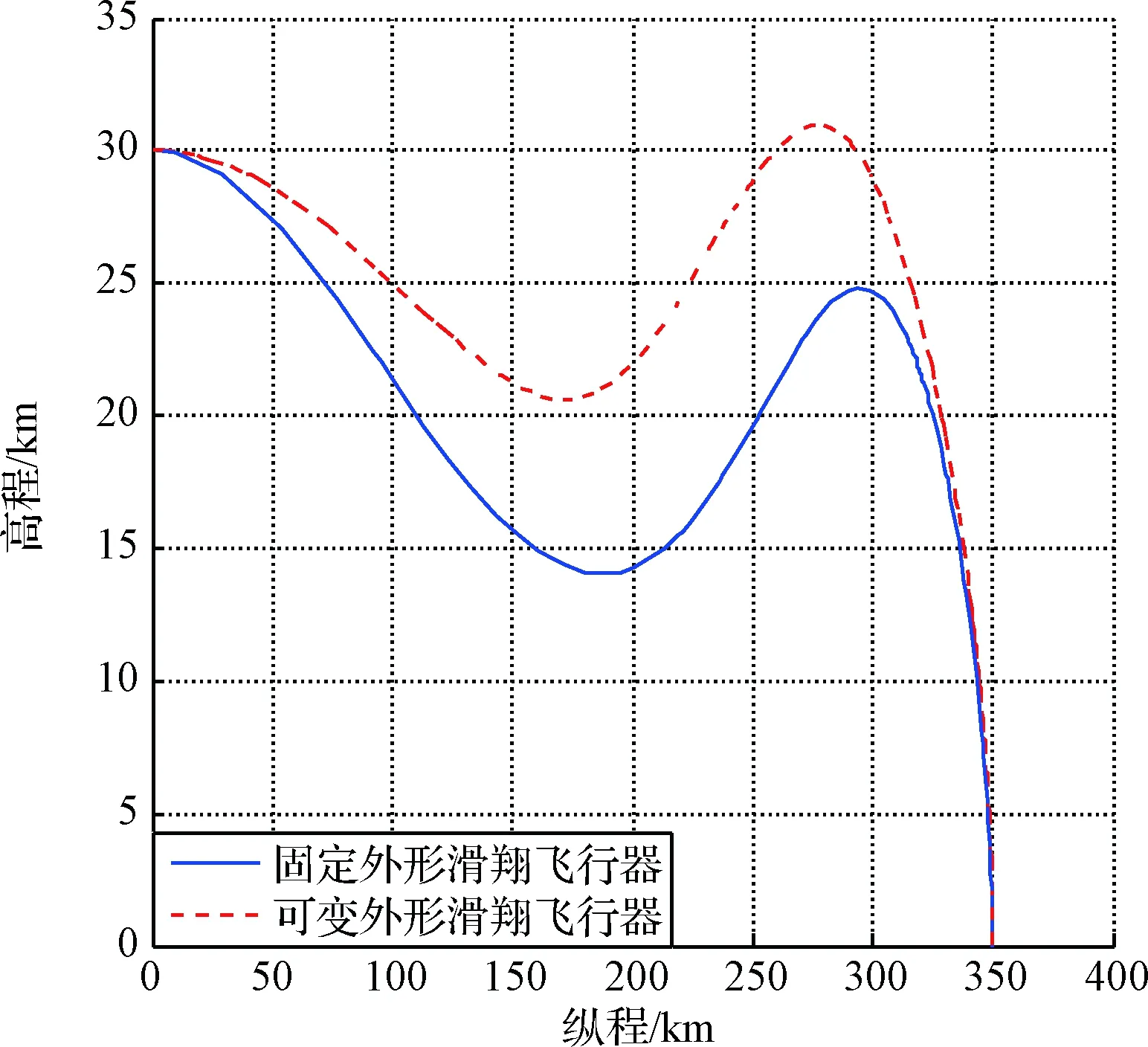
图15 末段下压轨迹Fig.15 The terminal trajectory

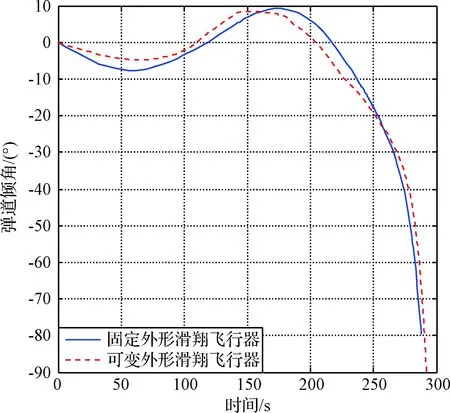
图16 弹道倾角变化曲线Fig.16 Track inclination curve

如图15所示，MGV与固定外形滑翔飞行器均能命中目标，但在终端速度和过载限制下，固定外形飞行器轨迹终点的最小轨迹倾角为-79.6°，而MGV的最小轨迹倾角可达-90°(见图16)，对加固目标和地下深层目标的打击效果更好。

4 结束语

本文分析了临近空间滑翔飞行器的变形需求，建立了MGV的冗余控制变量轨迹优化模型，利用伪谱法量化分析了射程覆盖、规避绕飞和末段打击几种典型作战想定下MGV的性能提升，结果表明变形技术的引入有效提升了飞行器的环境适应性和综合战技指标。在滑翔能力方面，MGV的最大纵程增加17.6%，最大横程增加41.6%，射程覆盖范围和起滑窗口面积增加了95.3%。机动能力方面，MGV的打击“盲区”缩小了37.5%；在弹道拉起段、弹道下压段提供更大的可用过载，有利于实现主动段与滑翔段、滑翔段与末制导段的平稳可控交接；在末制导段，更容易实现垂直灌顶攻击。同时，轨迹优化结果给出了飞行过程中的最优变形律，可以指导变形策略的制定和变形控制系统的设计，能够为变形技术在滑翔飞行器上的方案设计和工程应用提供一定的参考。